この記事を読むとわかること
・5と8の和で表すことのできない最大の整数は何か
・算数で解いた場合の解法
・数学で解いた場合の解法
最近こんなツイートがバズっているのを見かけました↓
小2長男「算数の問題教えて。」
俺「いいよー。どんな問題?」
長男「5と8の和で表すことができない最大の整数を求めよ。」
俺「!?」小4向けの問題集だけど大学入試で出てもおかしくないレベル。なかなか良問だった。
— 吉田匠 (@takuYSD) January 27, 2019
「大学入試で出てもおかしくないレベル」とまではいかないとは思いますが、算数によっても解けるし数学によっても解けるという面では誰でも楽しめる問題だなと感じました。
そして、数学の知識があれば暗算で解けてしまうので、数学が算数よりも優れている部分を感じられるでしょう。
この記事ではこの問題について算数・数学の2通りの解法で解説していきたいと思います!
5と8の和で表せない最大の整数は?
そもそも問題の意味は?
このツイートへのリプライを見ると、そもそも問題の意味がわからないという人が多かったので、問題の意味を説明します。
たとえば、18という数は、
\[5+5+8=18\]
と書けるので、5と8だけの和で表される数です。しかし、17はこのような形で表すことができません。
「17のように5と8の足し算だけで表すことができない整数がありますが、このような数には実は最大値が存在しています。それはなんでしょうか求めてくださいね」というのが噛み砕いた表現です。
数学的な問題文にするならば以下のようになります。
$x,\,y$を$0$以上の整数として、
\[5x+8y\]
の形で書けない整数の中で最も大きいものを求めよ。
ずばり答えは27
この問題の答えは27になります。
どうして答えが27になるんでしょうか?算数的な解き方、数学的な解き方の2通りを紹介したいと思います!
算数的な解法
まずは算数的な解法を紹介したいと思います!
5列に数字を書き並べる
この手の問題は2つの数字どちらかを選んで、その数の列に並べるのが最初の作業です!今回は、5と8なので、5列に並べると良いでしょう。
実際に並べるとこんな感じになります。

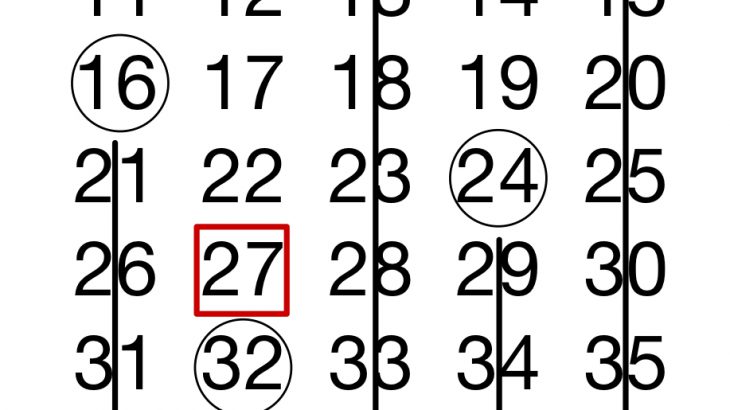
表せる数を見つけてその下を全部消す
5列に数を書き並べたのは、「1つ表せる数を見つけたらその下に書いてある数は全部表せると分かるから」です。例えば、24という数は、8を3回足せば表せます。こういう数に◯をつけておきましょう。
すると、24の下に書いてある29は、これに5を足せば表せます。その下に書いてある34はさらにもう一回5を足せば表せます。その下は…
というように、1つ表せる数を見つければその下に書いてある数は5を足していけば表せることがわかりますね!
これをやっていくと、以下のようになります。
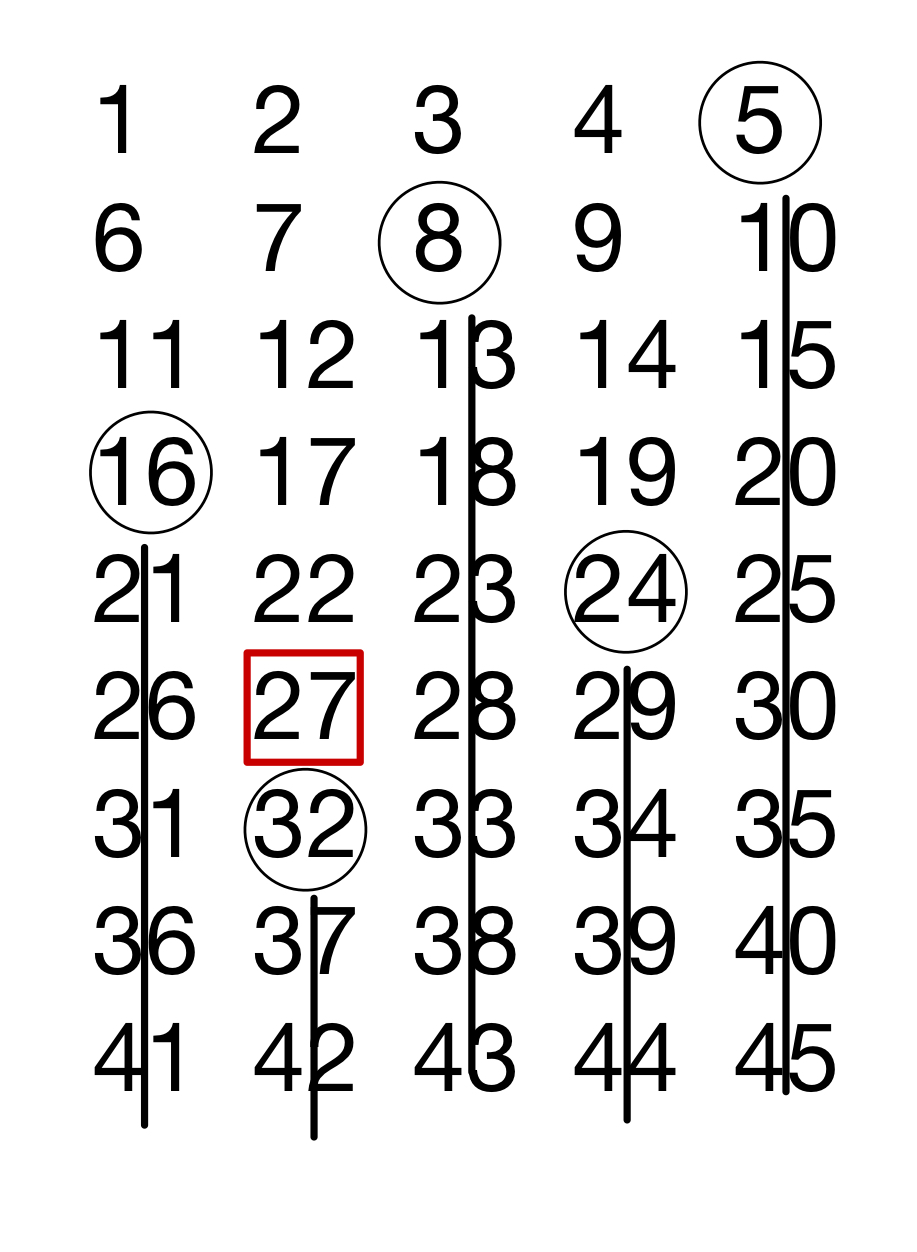
したがって、表すことのできない最大の数は27だということが一目瞭然ですね!これが算数的解法になります。
数学的な解法
ここからは数学的な解法について説明していきます。まず、与えられた問題は1次不定方程式に関する問題です。
不定方程式についての知識がない方はこちらの記事がおすすめです↓
不定方程式についての知識があるものとして、以下、解説を進めていきます。
x,yが0以上という条件がなければ任意の整数を表せる
今回の問題では、$x,\,y$が0以上という条件がついているのが普通の不定方程式と異なるところです。もしこの条件がなかったとすると、$5$と$8$が互いに素であることから、任意の整数を$5x+8y$の形で表すことが可能でですよね。
もう少し具体的には、ある整数$m$を
\[5x+8y=m\]
の形で表したいとき、$(x,\,y)=(-3,\,2)$のときに$5x+8y=1$となることから、$(x,\,y)=(-3m,\,2m)$とすることで表せることがわかります。
このような表し方は1通りではなく、$5\times8=40$であることを用いると、$k$を整数として、
\[(x,\,y)=(-3m+8k,\,2m-5k)\]
の形で表せるものすべてが解となり、これを一般解と呼ぶんでしたね。
kの値を調整してもx,yを0以上にできないギリギリが最大値
大きな自然数では、$k$の値を調整することで、$x,\,y$の値をどちらも0以上にすることが可能です。このような数のことを今回の問題では「5と8の和で表せる整数」と表現してるんですね。
つまり、$k$の値を調整しても$x,\,y$を0以上にできない(つまり$x,\,y$が常に異符号である)ギリギリのときが求めたい最大値になります。
今回の説明で「異符号」という言葉を使っていますが、「0と正の数」「負の数」の2つのグループにわけたときに2数が異なるグループに属していることを異符号と読んでいます。
厳密には間違いであることに注意してください。
先ほどの一般解の形を考えれば、常に異符号である絶妙な状況というのは、ある$x,\,y$が異符号であり、かつ、$x$に$8$を足して$y$から$5$を引くと、どちらも符号が入れ替わってしまう時ですね。
よって、$x$は$-7$から$-1$までのどれかで、$y$は$0$から$4$までのどれかです。$5x+8y$を最大にするには、$y$として$4$を選び、$x$として$-1$を選べばいいので、求める最大値は、
\[-5+32=\boldsymbol{27}\]
となります。
これを一般化すれば、以下のようになります。
$a,\,b$を互いに素な自然数、$x,\,y$を$0$以上の整数として、
\[ax+by\]
の形で表すことができない整数のうち最大のものは、
\[ab-(a+b)\]
である。
これを覚えておけば今回と同様の問題は一瞬で解けるようになりますね!
まとめ
・5と8の和で表せない最大の整数は27
・算数的に解くなら、5列に数字を並べて消していく!
・数学的に解くなら$ab-(a+b)$に代入する!
大学入試では、整数問題はひらめきを必要とする難しい問題が多いです。そこで、私はひらめきのパターンに慣れるために、網羅的に整数問題を解いて学習していました。
私が使っていたのは、この「マスターオブ整数」という参考書です!共通テスト(旧センター試験)レベルの簡単な問題から難関大レベルまで幅広く整数問題について扱っていて、かなりおすすめできる参考書です。