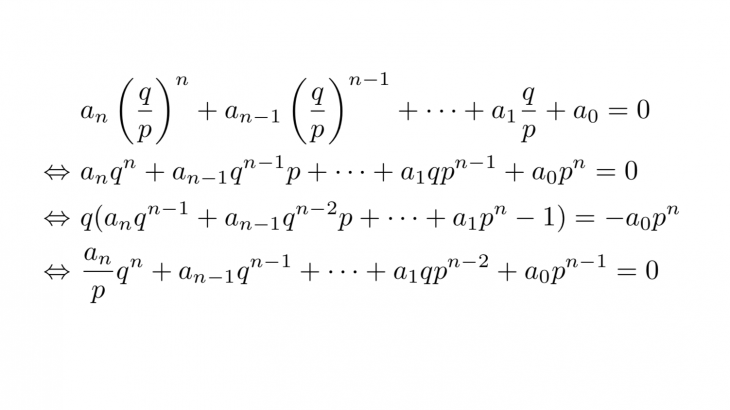この記事を読むとわかること ・有理数解とはそもそも何か ・有理数解や整数解に関わる定理 ・有理数解を持つ/持たないが関わる入試問題 方程式の有理数解 そもそも有理数解とは 有理数解とは、方程式の解のうち、2つの整数の分数の形で表せるようなもののことです。 入試問題ではしばしば、「この方程式が有理数解を持つような条件を求めよ」というような形式の問題が出題されることがあります。 こういった問題を解くた […]
この記事を読むとわかること ・東大数学の過去問をやるなら鉄緑会の問題集が圧倒的におすすめ! ・鉄緑会の問題集が赤本や青本よりもおすすめな5つの理由 東大数学の過去問問題集は何がおすすめ? 「東大数学の過去問を収録した本ってたくさんあってどれを選べばいいのかわからない!」というあなたに、現役東大医学部生の私、たわこがおすすめの過去問問題集を紹介します! 東大数学の過去問は鉄緑会が圧倒的におすすめ! […]
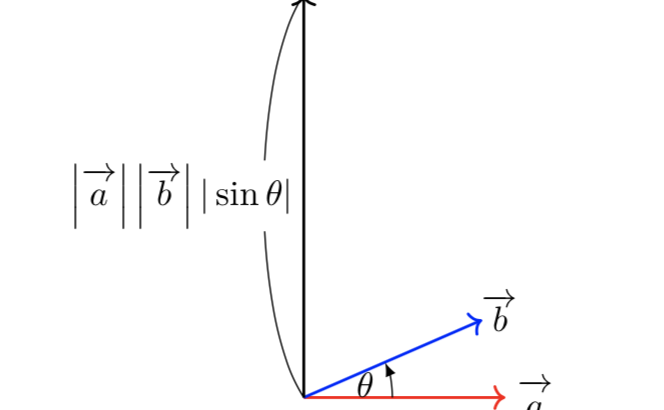
・ベクトルの外積とは何か ・外積を求めるための公式や覚え方 ・高校数学で外積が役立つ場面 ベクトルの外積とは? 外積とは2つのベクトルに垂直なベクトルの1つ ベクトルの外積とは、空間において2つのベクトル$\vec{a},\,\vec{b}$が与えられたときに、2ベクトルのなす角を$\theta$とすると、両方のベクトルに垂直な大きさが$|\vec{a}||\vec{b}||\sin{\theta […]
この記事を読むとわかること ・平面のベクトル方程式の表し方2通り ・ベクトル方程式から平面の方程式への変換のしかた 平面のベクトル方程式の表し方2通り 法線ベクトルを用いた平面のベクトル方程式 平面のベクトル方程式の表し方として最も簡単なものは、法線ベクトル(平面に垂直なベクトル)を用いたものです。 平面の法線ベクトルの1つを$\vec{n}$とすると、平面上の点の任意の点の位置ベクトルを$\ve […]