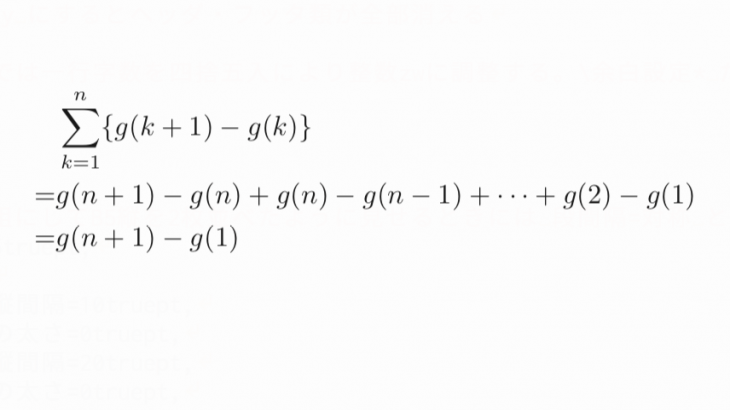この記事を読むとわかること ・数列の和の中抜けとはどんな手法か ・分数数列の総和の求め方 ・連続整数の積の総和の和の中抜けを用いた求め方 ・等差数列×等比数列の総和の和の中抜けを用いた求め方 和の中抜けとは g(k+1)-g(k)を満たす関数g(k)を探して総和を求める方法 和の中抜けとは、数列の一般項を$g(k+1)-g(k)$の形に変形できるような関数$g(k)$を探し、そのような$g(k)$ […]
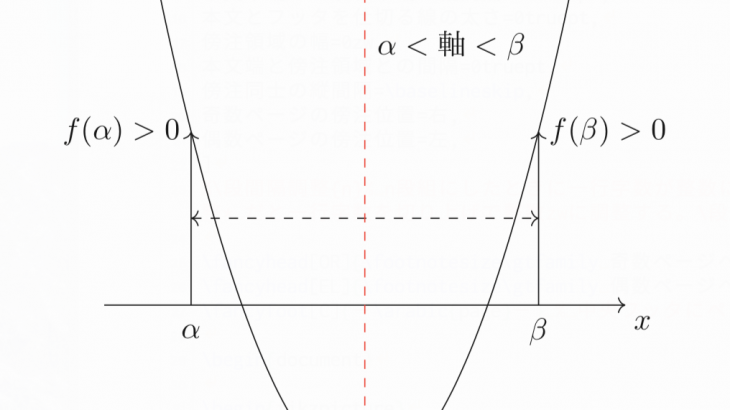
この記事を読むとわかること ・解の配置問題のパターン ・各パターンに対応した例題とその解き方 ・解の配置問題の実際の解答 解の配置問題のパターン一覧 解の配置問題とは、定められた範囲に決められた数だけ方程式が実数解を持つための条件を求める問題です。解の配置問題の典型的な問題のパターンには以下の4種類があります。 解の配置問題の4パターン ・ある範囲に異なる2実数解を持つ ・ある範囲にただ1つの実数 […]
フェルマーのクリスマス定理を拡張して証明してみる そもそもフェルマーのクリスマス定理とは フェルマーのクリスマス定理とは、かの有名な数学者ピエール・ド・フェルマーが証明した、「平方数の和で表される素数の条件」に関する定理です。 フェルマーのクリスマス定理 ある素数$p$が \[p=a^2+b^2(a,\,bは0でない整数)\] の形で書けることは、「$p=2$または$p$が$4$で割って$1$余る […]
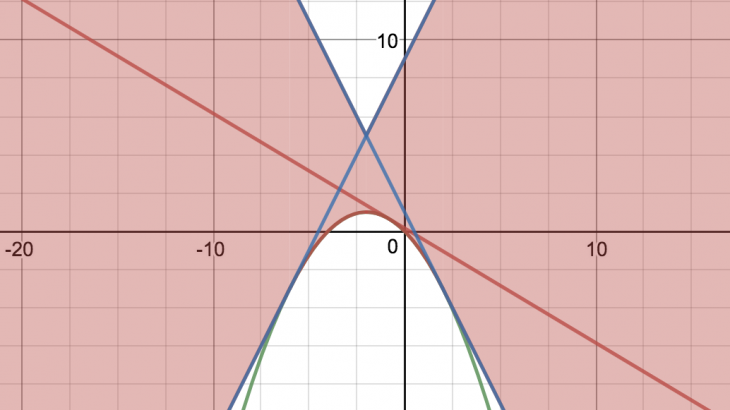
この記事を読むとわかること ・順像法・逆像法がどのようなものなのか ・順像法・逆像法を使った問題の解き方 ・順像法・逆像法の図解 ・順像法と逆像法の使い分け 順像法・逆像法とは? 順像法とはスライスして領域を求めるやり方 順像法とは、簡単に言えば、ある軌跡・領域を求めるために、その図形をスライスしたときに現れる線分の集まりとして図形の形を求めるやり方のことを指します。 より具体的には、$x$を固定 […]
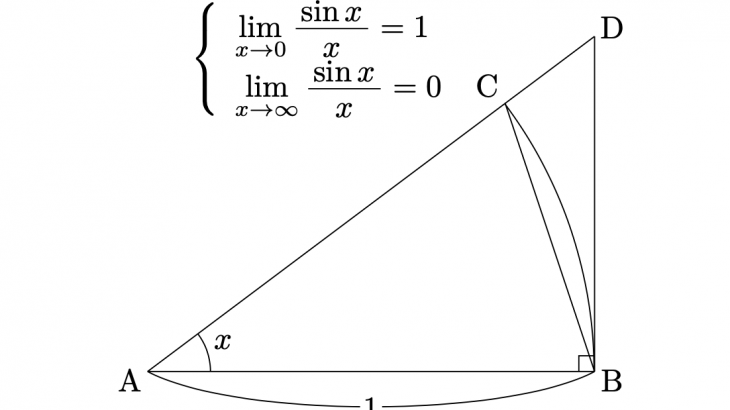
この記事を読むとわかること \[\lim_{x\to 0}\frac{\sin{x}}{x}=1\] \[\lim_{x\to \infty}\frac{\sin{x}}{x}=0\] ・sinx/xの極限の証明 ・sinx/xの極限を高校数学の範囲内で循環論法にならずに証明する方法 lim(x→0)sinx/xの極限値は? $\lim_{x\to 0}\frac{\sin{x}}{x}=1$にな […]