・ベクトルの外積とは何か
・外積を求めるための公式や覚え方
・高校数学で外積が役立つ場面
ベクトルの外積とは?
外積とは2つのベクトルに垂直なベクトルの1つ
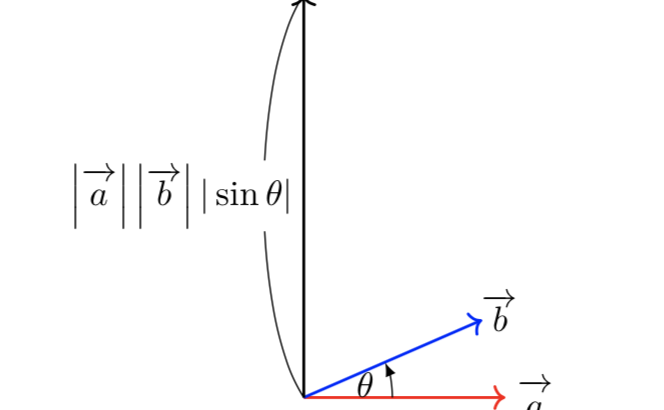
ベクトルの外積とは、空間において2つのベクトル$\vec{a},\,\vec{b}$が与えられたときに、2ベクトルのなす角を$\theta$とすると、両方のベクトルに垂直な大きさが$|\vec{a}||\vec{b}||\sin{\theta}|$のベクトルのことを指します。
ベクトルの内積はスカラー(単なる数値)だったのに対し、外積はベクトルであることに注意しましょう。
外積を求めるときの演算には×の記号を使います。例えば、$\vec{a}$と$\vec{b}$の外積は、
\[\vec{a}\times\vec{b}\]
と表されます。
しかし、よく考えてみると上の条件を満たすようなベクトルは2つあり一意に定まりません。
そこで、$\vec{a}$から$\vec{b}$の向きに右ねじを回したときにネジの進む向きとなっているベクトルの方を外積ベクトルとする定められています。
$\vec{a}\times\vec{b}=\vec{b}\times\vec{a}$とはならないことに注意しましょう。上の定義から逆向きのベクトルが出てくることになります。
述べてきたことをまとめると、以下のようになります。
2つのベクトル$\vec{a},\,\vec{b}$に対して、外積$\vec{a}\times\vec{b}$は大きさが$\left|\vec{a}\right|\left|\vec{b}\right||\sin{\theta}|$で両方のベクトルに垂直なベクトルのうち、$\vec{a}$から$\vec{b}$に右ねじを回したときにねじが進む向きのものである。
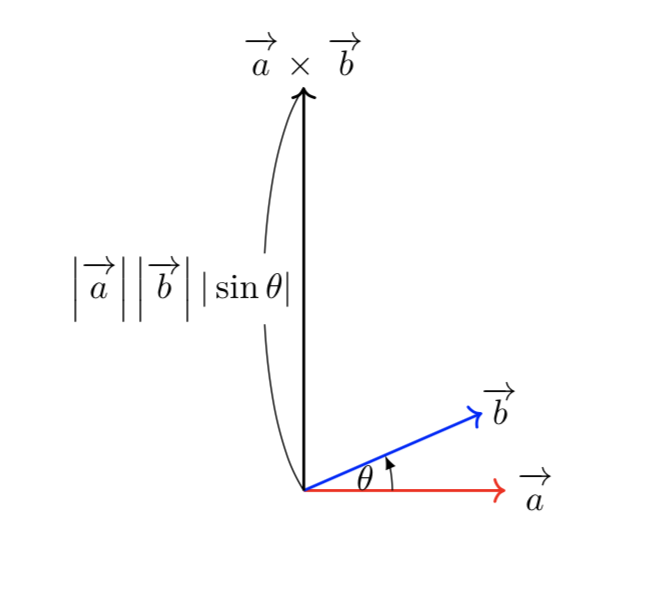
2つのベクトルが平行なときや、2つのベクトルのうちの少なくとも一方が零ベクトルである時には、外積は零ベクトルになることに注意しましょう。
外積の公式は?
外積の定義は分かったものの、このままでは実際に求めるときに非常に大変になってしまいます。そこで、外積を求めるための公式を覚えましょう。
と成分表示されるとき、
\[\vec{a}\times\vec{b}=(a_2b_3-b_2a_3,\,a_3b_1-b_3a_1,\,a_1b_2-b_1a_2)\]となる。
外積の公式の覚え方
外積の公式の覚え方は、「求めたい成分以外のたすき掛け」というのがおすすめです。これについて解説していきます。
例えば、
\[\vec{a}=(2,\,5,\,1),\,\vec{b}=(3,\,2,\,1)\]
という2つのベクトルの外積の$x$成分を求めたいときには、「$x$成分以外のたすき掛け」をすればよく、
\[5\times 1-2\times 1=3\]
となります。
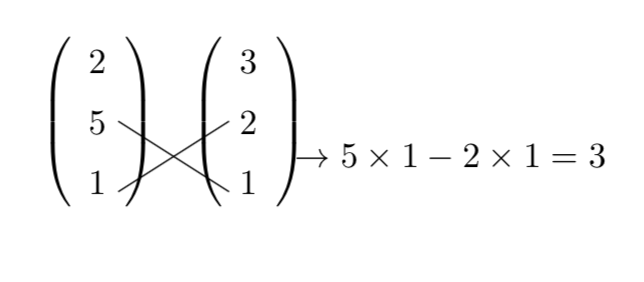
$z$成分も同様にして、
\[2\times 2-3\times 5=-11\]
と計算できます。
ただし、$y$成分を求める時のみ注意が必要です。$x$成分と$z$成分でたすき掛けをするのには変わりはありませんが、$z$成分が上に、$x$成分が下にくるように計算しなければなりません。
したがって、下図のように、$x$成分を$z$成分の下に書いてたすき掛けをすると計算しやすくなるでしょう。
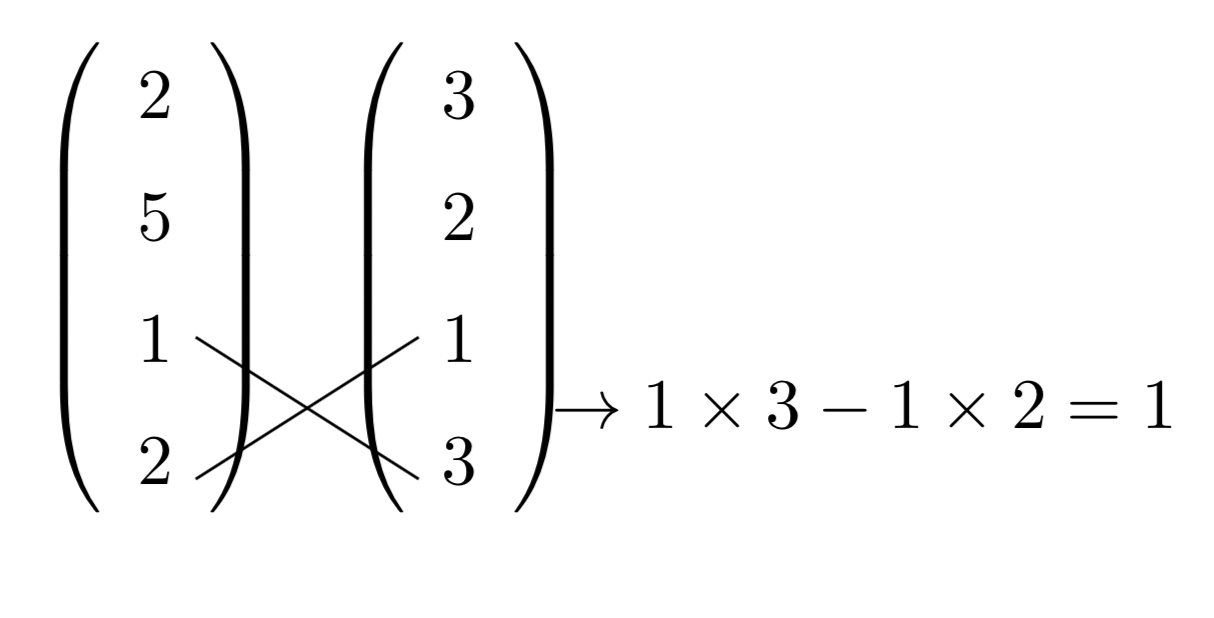
外積の公式は「求めたい成分以外のたすき掛け」と覚える!ただし、$y$成分を求めるときは$x$成分を$z$成分の下に書かなければいけないことに注意!
外積が高校範囲の数学で役立つ場面は?
外積は大学範囲の数学の知識ですが、高校数学ではどのような場面で役立つのでしょうか?主にこの2つの場面があります。
外積が高校数学で役立つ場面2つ
・平面の法線ベクトルの1つを求めるとき
・空間において平行四辺形や三角形の面積を求めるとき
平面の法線ベクトルの1つを求めるとき
外積は2つのベクトルに垂直なベクトルの1つになるので、その2ベクトルによって張られる平面の法線ベクトルを公式によってただちに求めることができます。
さらに、法線ベクトルが求まると平面の方程式をベクトル方程式から簡単に求めることができるので、平面の方程式を求めるのにも役立つわけです。
外積を利用した平面の方程式の求め方についてはこちらの記事を読んでください。
空間において平行四辺形や三角形の面積を求めるとき
外積の大きさは2ベクトルによって作られる平行四辺形の面積に等しいので、外積ベクトルを求めてからその大きさを求めることによって平行四辺形やそれを対角線で切った三角形の面積を求めるのに役立ちます。
ただ、2つのベクトルによってできる三角形の面積を求める場合には、
\[\frac{1}{2}\sqrt{\left|\vec{a}\right|^2\left|\vec{b}\right|^2-\left(\vec{a}\cdot\vec{b}\right)^2}\]
の公式も有効です。これを2倍すれば当然平行四辺形の面積になります。面積を求める場合には外積の公式かこの公式のどちらかを用いればよいでしょう。
2つのベクトル
\[\vec{a}=(a_1,\,a_2,\,a_3),\,\vec{b}=(b_1,\,b_2,\,b_3)\]
によって作られる三角形を求めるときには、
\[\vec{a}\times\vec{b}=(a_2b_3-b_2a_3,\,a_3b_1-b_3a_1,\,a_1b_2-b_1a_2)\]
の大きさを求めるか、
\[\frac{1}{2}\sqrt{\left|\vec{a}\right|^2\left|\vec{b}\right|^2-\left(\vec{a}\cdot\vec{b}\right)^2}\]
を計算する。
まとめ
・外積とは2ベクトル$\vec{a},\,\vec{b}$に垂直なベクトル
・外積の大きさは$\vec{a},\,\vec{b}$のなす角を$\theta$として$\left|\vec{a}\right|\left|\vec{b}\right||\sin{\theta}|$
・外積の向きは$\vec{a}$から$\vec{b}$に右ねじを回したときにネジが進む向き
・平面の法線ベクトルを用いるときに外積は有効
・三角形や平行四辺形の面積を求めるときにも外積は役立つが
\[\frac{1}{2}\sqrt{\left|\vec{a}\right|^2\left|\vec{b}\right|^2-\left(\vec{a}\cdot\vec{b}\right)^2}\]
の公式も有用なので、どちらかを使うようにすればよい