この記事を読むとわかること
・条件付き確率とは何なのか
・条件付き確率と独立の関係
・条件付き確率の公式による求め方
・条件付き確率を知らないと絶対に間違えてしまう問題
・条件付き確率を効率よく計算するコツ
・条件付き確率が関わる入試問題
条件付き確率の求め方とは?
そもそも条件付き確率とは
条件付き確率とはある事象Aが起こったという条件下での、ある事象Bが起こる確率のことを指します。一般に数式では、$P_A(B)$と書きます。
例えば、10本のうち1本が当たりであるくじ引きがあるときに、「2番目にくじを引く人が当たりを引く確率」と「『1番目にくじを引いた人が当たりを引いた』という条件下で、2番目にくじを引く人が当たりを引く確率」は全く異なることを考えれば、条件付き確率が何なのかわかりやすいかと思います。前者は$\frac{1}{10}$で、後者は当たりを引く可能性はないので$0$になりますよね。
条件付き確率の公式による求め方
条件付き確率は以下の公式で求めることができます。
事象Aが起こる確率を$P(A)$、事象AとBがどちらも起こる確率を$P(A\cap B)$とすると、事象Aが起こったという条件のもとでの、ある事象Bが起こる条件付き確率は、
\[P_A(B)=\frac{P(A\cap B)}{P(A)}\]
で求められる。
数式だと覚えづらいという人は言葉で覚えておいてもよいでしょう。
\[\frac{AもBも起こる確率}{Aが起こる確率}\]
条件付き確率と独立との関係
条件付き確率$P_A(B)$を求めると、それが$P(B)$と等しくなることがあります。
これは、「Aが起こった」という条件が事象Bの起こる確率に全く影響を及ぼさないということを意味するので、このとき「事象Aと事象Bは独立である」と言います。
AとBが独立であるとき、
\[P(B)=P_A(B)=\frac{P(A\cap B)}{P(A)}\]
が成り立ち、分母を払えば、
\[P(A)\cdot P(B)=P(A\cap B)\]
となるので、2つの事象が独立であるかどうかを調べたいときはこの式が成立するかをチェックしましょう。
条件付き確率を知らないと絶対に間違えてしまう問題
条件付き確率を「公式を覚えていれば求められるもの」という認識でいると大学受験などの場面で痛い目に遭うと思います。なぜなら、条件付き確率の問題の難しさは、条件付き確率の問題であることに気づくことにあるからです。これがこの記事の中で最も重要なことと言っても過言ではないでしょう。
そうは言っても、その難しさというのを人生の中で体感したことがない人がほとんどだと思います。
そこで、条件付き確率を理解していないと絶対に間違えてしまう問題を2つ紹介しておくことによって、その難しさを実感しておきましょう!
問題1

よくある誤答
「男の子が生まれたからといって、他の子供の性別がどうなるかの確率が上がったり下がったりするわけないでしょ。だから $\frac{1}{2}$に決まってるじゃん。」
と思った方、それはよくある誤答です。
大事なことなので改めて言いますが、条件付き確率というのはもちろん公式を覚えてそれ通りに計算すれば求まるのですが、そもそも条件付き確率の問題であるということを気づくのが難しいのです。
この問題の答えは$\frac{1}{3}$になります。どうして$\frac{1}{2}$にならないのでしょうか?
解答・解説
2人の子供の性別の組み合わせというのは以下の4パターンあって、どれも等しく$\frac{1}{4}$になっています。
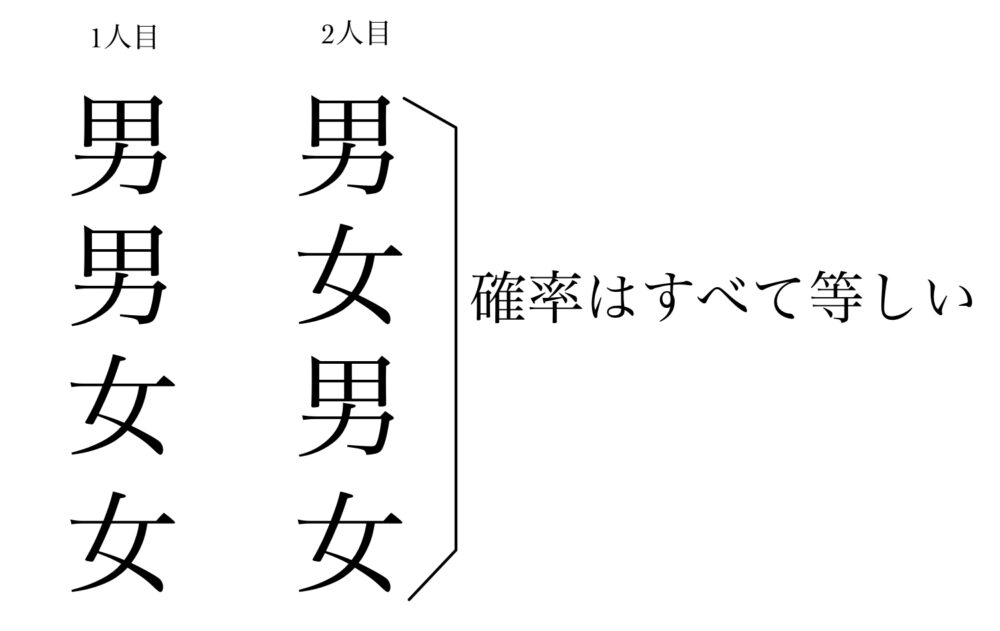
さて、今与えられているのは、片方の子供が男の子という情報です。この男の子というのは1人目であるのか2人目であるのかという情報は分かっていないので、男男、男女、女男の3パターンに絞られている状態になります。
よって、もう一人の性別がどうなっているのかを見ていけば、3パターンのうち、もう一人が男であるパターンというのは1パターンしかないので、確率は$\frac{1}{3}$になることが分かるかと思います。
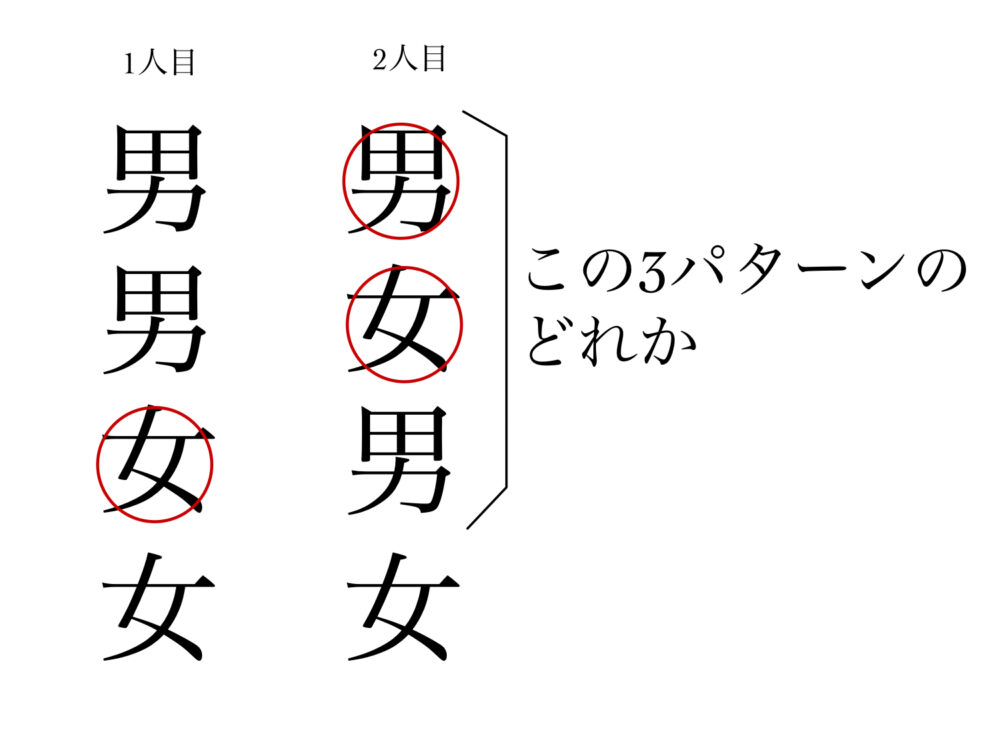
さて、条件付き確率の公式を使ってこの問題を解いていきましょう。
今求めたいのは、「2人の子供のうち片方が男であるという条件のもとでの、もう一人の子供が男であるという条件付き確率」ですね。よって、公式に当てはめれば、
\[\frac{(2人の子供の両方が男である確率)}{(2人の子供のうち片方が男である確率)}\]
を求めればよいことになりますね。
よって、2人の子供のうち片方が男である確率は、同様に確からしい4パターンのうちの3パターンであるから$\frac{3}{4}$、また、2人の子供の両方が男である確率は$\frac{1}{4}$になるので、求める条件付き確率は、
\[\frac{\frac{1}{4}}{\frac{3}{4}}=\boldsymbol{\frac{1}{3}}\]
となります。
これで条件付き確率の問題であることに気づくのが難しいというのはかなり理解できたんじゃないでしょうか?
これくらいの問題であれば簡単に答えが$\frac{1}{3}$になることを見抜けたという人は次の問題にも取り組んでみてください。次の問題はもう少し複雑なので、面倒な人は読み飛ばしてください。
問題2

よくある誤答
「最初は男女同数ずついたんだから、確率は$\frac{1}{2}$になるに決まってるでしょ」
と思った方がほとんどではないでしょうか?もちろんこの問題の答えも$\frac{1}{2}$ではありません。
この問題も求めるものは条件付き確率なのですが、なかなか条件付き確率の問題であることには気づきづらいです。与えられている条件とは、「2回目〜4回目に男が帰った」というものですが、これは最初に誰が帰るかを決めるときよりも時系列的にあとなので、直感的には2つの事象が独立であると勘違いしてしまいがちです。
こういった時系列的な逆転があると、条件付き確率となっていることに気づきづらいことを覚えておくとよいでしょう。
さて、なぜ確率が$\frac{1}{2}$にならないのでしょうか?
最初に男女50人ずつという状態から始まりましたが、30人ずつだったらどうでしょうか?同じく$\frac{1}{2}$だと思いますか?
10人ずつだったらどうでしょうか?同じく$\frac{1}{2}$だと思いますか?
では3人ずつだったらどうでしょうか?
最初に男が帰っている確率が$\frac{1}{2}$だったら、そのあと男が3人帰っているので、「男女3人ずついる状態から$\frac{1}{2}$の確率で男が4人帰る」というおかしな状態になってしまいます。
これで、この問題の答えが$\frac{1}{2}$にはならないということが理解できたのではないでしょうか。
解答・解説
条件付き確率の公式を使って正しい答えを求めましょう!
今求めたいのは、「2回目〜4回目に男が帰るという条件のもとで、1回目に男が帰る条件付き確率」ですね。よって、公式に当てはめれば、
\[\frac{1回目〜4回目すべてで男が帰る確率)}{(2回目〜4回目に男が帰る確率)}\]
を求めればよいことになりますね。
2回目〜4回目に男が帰る確率は、1回目に男が帰る場合と女が帰る場合の2パターンがあることに注意すれば、
\[\frac{50}{100}\cdot\frac{49}{99}\cdot\frac{48}{98}\cdot\frac{47}{97}+\frac{50}{100}\cdot\frac{50}{99}\cdot\frac{49}{98}\cdot\frac{48}{97}=\frac{12}{99}\]
と求まります。
そして、1回目〜4回目すべてで男が帰る確率は、
\[\frac{50}{100}\cdot\frac{49}{99}\cdot\frac{48}{98}\cdot\frac{47}{97}=\frac{12\cdot47}{99\cdot97}\]
であるので、求める条件付き確率は、
\[\frac{\frac{12\cdot47}{99\cdot97}}{\frac{12}{99}}=\boldsymbol{\frac{47}{97}}\]
となります。
以上のような、直感に反する確率の問題を覚えておくことによって、条件付き確率の問題というのはそれが条件付き確率の問題であると気づくのが難しいのであるということを理解しておくのが重要です。
条件付き確率を効率よく求めるコツ
条件付き確率を求めるときには、計算の際のちょっとしたコツがあります。それについて解説していきます。
条件付き確率の分母となる$P(A)$を計算するときには、場合分けが必要となることが多いです。この場合分けの際に、分子となる$P(A\cap B)$を求めることになるケースが非常に多いです。
そのため、分子の確率を求める際に、分母を求める途中過程を参照するだけでよいかどうかに注意を払うと効率よく条件付き確率を求めることができます。
先程の男女50人ずつの問題を例に取ると、2回目〜4回目に男が帰る確率を求めるためには、1回目に男が帰る場合と女が帰る場合の2パターンに場合分けをする必要がありますが、条件付き確率の分子は、1回目に男が帰る場合と等しいので計算すべき項目は実は2つしか出てきません。
このように、分母を求めるときに分子にあたる確率を求める必要がある時が多いということを意識しておくと効率よく条件付き確率を計算することができます。
条件付き確率が関わる入試問題
条件付き確率の求め方が分かったら、入試問題を解いてみましょう!
問題1

解答・解説
2020年センター試験(共通テスト)数学ⅠA第3問の問題です。
3番の選択肢が条件付き確率に関わるものになっていますね。条件付き確率だと気づかずに単に「オモテが出る確率」だと思ってしまうと、正しい選択肢に見えてしまうので気をつけましょう。
(この問題はコインの表裏が同じ確率で出ることが明言されていませんが、等確率で出るものだと思って解いてください。)
解説は以下の記事にあります。
問題2

解答・解説
2019年センター試験(共通テスト)数学ⅠA第3問の問題です。
袋の中から玉を取り出していくという確率の問題では非常によくある設定の問題で、(4)で条件付き確率について問われています。丁寧に場合分けをしていけば特に問題なく解けるでしょう。
解説は以下の記事にあります。
問題3

解答・解説
2016年度東大理系数学第2問の問題です。(2)が条件付き確率を求める問題になっています。
条件付き確率の定義にしたがって計算をしていくことになりますが、分母や分子の確率を求めるためにシグマの計算をしなければならないので少しだけ面倒です。東大の確率の問題の中ではかなり解きやすい部類のものだと思うので、難関大志望の人はぜひ解ききりたいところです。
解説は以下の記事にあります。
まとめ
・条件付き確率とは、ある事象Aが起こったという条件のもとで事象Bが起こる確率のこと
・条件付き確率の公式
\[P_A(B)=\frac{P(A\cap B)}{P(A)}\]
・事象Aが起こったかどうかが事象Bの起こる確率に影響しないことを「独立」と呼ぶ
・条件付き確率は、条件付き確率の問題であることを見抜くのが難しい
・公式の分母にあたる部分を求めるときに分子の確率が求まることがあるので、それに気づくと計算が楽になる





