フェルマーのクリスマス定理を拡張して証明してみる
そもそもフェルマーのクリスマス定理とは
フェルマーのクリスマス定理とは、かの有名な数学者ピエール・ド・フェルマーが証明した、「平方数の和で表される素数の条件」に関する定理です。
フェルマーのクリスマス定理
ある素数$p$が
\[p=a^2+b^2(a,\,bは0でない整数)\]
の形で書けることは、「$p=2$または$p$が$4$で割って$1$余る数であること」と同値である。
メルセンヌ素数でよく知られているメルセンヌに、フェルマーがこの証明を報告するべく手紙を送ったのが1640年12月25日であったことから、フェルマーのクリスマス定理と名がついたそうです。
フェルマーのクリスマス定理を拡張してみる
フェルマーのクリスマス定理の証明は可換環の概念を導入することによって証明ができますが、その証明の過程を見ると、定理を拡張して、以下の命題も証明できそうです。
フェルマーのクリスマス定理の拡張
ある素数$p$が
\[p=a^2+ab+b^2(a,\,bは0でない整数)\]
の形で書けることは、「$p=3$または$p$が$3$で割って$1$余る数であること」と同値である。
この命題を証明している記事や論文などが見つからなかったので、私が証明してみました。(数学が専門ではないため、間違いなどありましたら指摘してください。)
証明全体の流れ
証明全体の流れは下の通りです。ただし、$p=3$のときは$a=b=1$とすれば成立し、$p=2$のときは、$p=a^2+ab+b^2$の形で表すことができないので、以下においては常に$3$より大きい素数$p$についてのみ考えるものとします。
(i)「$p\equiv 1(\mathrm{mod}~3)$」$\Leftrightarrow$「単項イデアル$(X^2+X+1)$が多項式環$\mathbb{F}_p[X]$の極大イデアルでない」を示す。
(ii)「単項イデアル$(X^2+X+1)$が多項式環$\mathbb{F}_p[X]$の極大イデアルでない」$\Leftrightarrow $ 「イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでない」を示す。
(iii)「イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでない」
$\Leftrightarrow$
「整数$a,\,b$を用いて、$p=a^2+ab+b^2$と表せる」を示す。
(i)の証明
まず、「多項式環$\mathbb{F}_p[X]$のイデアルはすべて単項イデアルである」……(Ⅰ)を示します。
(証明)$I$を多項式環$\mathbb{F}_p[X]$の任意のイデアルとします。
1. $I=\{0\}$のとき
$I=(0)$なので、たしかに単項イデアルです。
2. $I\ne {0}$のとき
$I$の元のうち0でないものが存在し、その中で次数が最小のものを$A(X)$とします。$I$の任意の元$f(X)$を$A(X)$で割ったときの商を$B(X)$、余りを$C(X)(B(X),\,C(X)\in\mathbb{F}_p[X])$とすると、
\[f(X)=A(X)B(X)+C(X)\]
を満たします。これを変形すると、
\[C(X)=f(X)-A(X)B(X)\]
となりますが、ここで、$A(X),\,f(X)\in I$かつ$B(X)\in\mathbb{F}_p[X]$より、$C(X)\in I$がわかります。
さらに、$C(X)$は$A(X)$よりも低次であること、および、$A(X)$が$I$の0でない元のうち最低次であることを踏まえると、
\[C(X)=0\]
したがって、$I$の任意の元$f(X)$は単項イデアル$(A(X))$の元であるので、
\[I\subset (A(X))\]
また、$A(X)\in I$であることから、
\[(A(X))\subset I\]
も成り立ちます。
以上を合わせて、$I=(A(X))$が言えます。
したがって、多項式環$\mathbb{F}_p[X]$の任意のイデアルは単項イデアルであることが示されました。
次に、「単項イデアル$(X^2+X+1)$が多項式環$\mathbb{F}_p[X]$の極大イデアルでない」$\Leftrightarrow$「$X^2+X+1=(X-a)(X-b)$を満たす有限体$\mathbb{F}_p$の元$a,\,b$が存在する」を示します。
(証明)
1.「$X^2+X+1=(X-a)(X-b)$を満たす有限体$\mathbb{F}_p$の元$a,\,b$が存在する」$\Rightarrow$「単項イデアル$(X^2+X+1)$が多項式環$\mathbb{F}_p[X]$の極大イデアルでない」の証明
$X^2+X+1=(X-a)(X-b)$より、単項イデアル$(X-a)$は、
\[\mathbb{F}_p[X]\varsupsetneq(X-a)\varsupsetneq(X^2+X+1)\]
を満たすので$(X^2+X+1)$は極大イデアルではありません。
2.「単項イデアル$(X^2+X+1)$が多項式環$\mathbb{F}_p[X]$の極大イデアルでない」$\Rightarrow$「$X^2+X+1=(X-a)(X-b)$を満たす有限体$\mathbb{F}_p$の元$a,\,b$が存在する」の証明
$(X^2+X+1)$は$\mathbb{F}_p[X]$の極大イデアルでないので、
\[\mathbb{F}_p[X]\supsetneq I\supsetneq (X^2+X+1)\]
を満たすイデアル$I$が存在します。(Ⅰ)より、$I$は単項イデアルです。
よって、$I=(f(X))$なる$f(X)(\in\mathbb{F}_p[X])$が存在し、$I\supsetneq (X^2+X+1)$より、$f(X)$の次数は1で、1次の係数は1としてよいので、$f(X)=X-a$をみたす$a\in\mathbb{F}_p$が存在します。
よって、$X^2+X+1=(X-a)(X-b)$をみたす$b\in\mathbb{F}_p$も存在します。
以上より、「単項イデアル$(X^2+X+1)$が多項式環$\mathbb{F}_p[X]$の極大イデアルでない」$\Leftrightarrow$
「$X^2+X+1=(X-a)(X-b)$を満たす有限体$\mathbb{F}_p$の元$a,\,b$が存在する」が示されました。
ここで、上の$a,\,b$が$a\ne b$……(Ⅱ)を満たすことを示します。
(証明)
\[X^2+X+1=(X-a)(X-b)=X^2-(a+b)X+ab\]
より、有限体$\mathbb{F}_p$の元として、$a+b=-1かつab=1$が成り立ちます。
ここで、$a=b$と仮定すると、
\[\begin{align*}a=\frac{-1}{2}かつa^2=1\Leftrightarrow&a=\frac{-1}{2}かつ\frac{1}{4}=1\\
\Leftrightarrow&a=\frac{-1}{2}かつ1=4\\
\Leftrightarrow&a=\frac{-1}{2}かつ0=3\end{align*}\]
が成立します。
ところが、今、3より大きい素数$p$について考えているので、有限体$\mathbb{F}_p$上において$0=3$とはなり得ません。よって、元の仮定が誤りであり、$a\ne b$であることが示されました。
続いて、「$X^2+X+1=(X-a)(X-b)$を満たす有限体$\mathbb{F}_p$の元$a,\,b$が存在する」$\Leftrightarrow $「$X^{p-1}-1$が$X^2+X+1$で割り切れる」を示します。
(証明)$p$が素数であること、および、フェルマーの小定理より、有限体$\mathbb{F}_p$上の0に等しくない元$a$に対しては、
\[a^{p-1}-1=0\]
が成り立ちます。よって、
\[X^{p-1}-1=(X-1)(X-2)\cdots(X-p+2)(X-p+1)\]
と因数分解できることがわかります。
ここで、$a,\,b$は$ab=1$を満たすことより、$a\ne0$かつ$b\ne0$であることと、(Ⅱ)より、$X^2+X+1=(X-a)(X-b)$と因数分解できるとき、$X^{p-1}-1$は$(X-a)(X-b)$で割り切れます。すなわち、$X^2+X+1$で割り切れます。
逆に、$X^{p-1}-1$が$X^2+X+1$で割り切れるとき、上の因数分解の結果から、$X^2+X+1=(X-a)(X-b)$の形で表せることが即座に分かります。
最後に、「$X^{p-1}-1$が$X^2+X+1$で割り切れる」$\Leftrightarrow $「$p\equiv1~(\mathrm{mod 3})$」を示します。
(証明)
1.「$X^{p-1}-1$が$X^2+X+1$で割り切れる」$\Rightarrow$「$p\equiv1(\mathrm{mod 3})$」の証明
$X^{p-1}-1$が$X^2+X+1$で割り切れるとき、$p\equiv0,2~(\mathrm{mod~3})$であったと仮定します。
1-a.$p\equiv0~(\mathrm{mod~3})$のとき
3より大きい素数で、かつ、3で割り切れるものは存在しないので不適です。
1-b. $p\equiv2~(\mathrm{mod~3})$のとき
$p$は3より大きい素数でかつ、今、$p-2$は3の倍数であるので、
\[\begin{align*}X^{p-1}-1={}&X^{p-1}-X^{p-2}+X^{p-2}-1\\
=&X^{p-2}(X-1)+(X^3-1)(X^{p-5}+X^{p-8}\cdots+X^3+1)\\
=&X^{p-2}(X-1)+(X^2+X+1)(X-1)(X^{p-5}+X^{p-8}\cdots+X^3+1)\end{align*}\]
よって、$X^{p-2}(X-1)$が$X^2+X+1$で割り切れることが分かりますが、
\[0^2+0+1=1,\,1^2+1+1=3\]
より、$p$が3より大きいことも考慮すると、$X^2+X+1$は$x$も$X-1$も因数に持たないので、これはあり得ません。
よって、元の仮定が誤りであり、$p\not\equiv2(\mathrm{mod3})$
以上より、$p\not\equiv0,2(\mathrm{mod3})$が示されたので、「$X^{p-1}-1$が$X^2+X+1$で割り切れる」$\Rightarrow$「$p\equiv1~(\mathrm{mod~3})$」が示された。
2.「$p\equiv1~(\mathrm{mod~3})$」$\Rightarrow$「$X^{p-1}-1$が$X^2+X+1$で割り切れる」の証明
$p\equiv1(\mathrm{mod3})$および$p$は3より大きい素数であることから、自然数$n$を用いて$p=3n+1$と表せます。このとき、
\[\begin{align*}X^{p-1}-1=&X^{3n}-1\\
=&(X^3-1)(X^{3n-3}+X^{3n-6}+\cdots+1)\\
=&(X^2+X+1)(X-1)(X^{3n-3}+X^{3n-6}+\cdots+1)\end{align*}\]
よって、$X^{p-1}-1$が$X^2+X+1$で割り切れることが示されました。
以上より、「$X^{p-1}-1$が$X^2+X+1$で割り切れる」$\Leftrightarrow $「$p\equiv1~(\mathrm{mod~3})$」が示されました。
以上すべての議論を合わせると、
「$p\equiv 1(\mathrm{mod}3)$」$\Leftrightarrow$「単項イデアル$(X^2+X+1)$が多項式環$\mathbb{F}_p[X]$の極大イデアルでない」が証明されました。
(ii)の証明
「$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]/p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\simeq \mathbb{F}_p[X]/(X^2+X+1)$」を示せばよいです。
まず、$\mathbb{F}_p[X]/(X^2+X+1)\simeq \mathbb{Z}[X]/(p,\,X^2+X+1)$を示します。
(証明) $a$を可換環として、$I$をそのイデアルとします。また、$\bar{A}=A/I$とします。
このとき、$I\subseteq J\subseteq C$を満たす任意のイデアル$J$と$\bar{C}$のイデアル$\bar{J}$を取ります。
可換環の射$f:C\rightarrow \bar{C}|c\rightarrow c+I(c\in C)$について考えます。任意の$a’,\,b'(\in \bar{J})$、$c’\in C$に対して、$a’=a+I,\,b’=b+I,\,c’=c+I$となる、$a,\,b(\in J)$、$c(\in C)$が存在して、
\[a’+b’=(a+I)+(b+I)=a+b+I=f(a+b)\in f(J)\\c’a’=(c+I)(a+I)=ca+I=f(ca)\in f(J)\]
となることから、$f(J)$は$\bar{C}$のイデアルです。
$I$を含む$C$のイデアル$J_1,\,J_2$があって、$f(J_1)=f(J_2)$を満たすと仮定すると、$J_1$の任意の元$j_1$について、$f(j_1)=j_1+I=f(j_2)$を満たす$J_2$の元$j_2$が存在して、
\[j_1-j_2\in I\subseteq J_2 \]
を満たすので、$J_1\subseteq J_2$が分かります。
同様にして、$J_2\subseteq J_1$も分かるので、$J_1=J_2$
また、$f^{-1}(\bar{J})=J^{\ast}$とおくと、$I=0+I$より、$I$は$\bar{C}$の零元であるので、$I\subseteq \bar{J}$を満たします。よって、$f^{-1}(I)\subseteq J^{\ast}$が分かります。
任意の$a,\,b\in J^{\ast},\,c\in C$に対して、
\[f(a+b)=a+b+I=(a+I)+(b+I)\in \bar{J}\\
f(ca)=ca+I=(c+I)(a+I)\in \bar{J}\]
であるから、$J^{\ast}$は$C$のイデアルです。
以上より、$f$は全単射であることが分かりました。
ここで、$C=\mathbb{Z}[X],\,I=p\mathbb{Z}[X],\,J=(p,\,X^2+X+1)$とすれば、$\bar{J}=(X^2+X+1)$となって、それぞれの商環が1対1に対応するので、
\[C/J\simeq \bar{C}/\bar{J}\Leftrightarrow \mathbb{F}_p[X]/(X^2+X+1)\simeq \mathbb{Z}[X]/(p,\,X^2+X+1)\]
が成り立ちます。
次に、$\mathbb{Z}[X]/(X^2+X+1)\simeq \mathbb{Z}\left[\frac{-1+\sqrt{3}}{2}\right]$を示します。
(証明)$P\in \mathbb{Z}[X]$とすると、
\[P=(X^2+X+1)Q+R~(Q,\,R\in \mathbb{Z}[X],\,Rは1次以下の式)\]
なる$Q,\,R$がただ1組存在します。
よって、$\mathbb{Z}[X]/(X^2+X+1)$においては、$\bar{P}=\bar{R}$となるので、$\mathbb{Z}[X]/(X^2+X+1)$の元はすべて、
\[\alpha\bar{X}+\beta(\alpha,\,\beta\in \mathbb{Z})\]
ただ1通りに書き表せます。
同様に、$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の元は全て、
\[\alpha’\tfrac{-1+ \sqrt{-3}}{2}+\beta’~(\alpha’,\,\beta’\in\mathbb{Z})\]
の形に書き表せます。
ここで、$f:\mathbb{Z}[X]\rightarrow \mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]|X\rightarrow \frac{-1+ \sqrt{-3}}{2}$なる可換環の射$f$を定めれば、$f(X^2+X+1)=0$より、商環の普遍性から、商環への標準全射$p:X\rightarrow \bar{X}$に対して、$f=\bar{f}\circ p$なる可換環の射$\bar{f}$がただ一つ存在して、この場合$\bar{f}:\mathbb{Z}[X]/(X^2+X+1)\rightarrow \mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]|\bar{X}\rightarrow \frac{-1+ \sqrt{-3}}{2}$です。
上の議論から、$\bar{f}$は全単射であることが分かるので、$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\simeq \mathbb{Z}[X]/(X^2+X+1)$が示されました。
以上の議論をまとめて、$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]/p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\simeq \mathbb{F}_p[X]/(X^2+X+1)$が証明されました。
(iii)の証明
まず、$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$のイデアルはすべて単項イデアルであることを示す。
(証明)0でない$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$のイデアル$I$の要素のうち絶対値が正で最小のものを$\alpha$とします。また、ここでは$\omega=\frac{-1+ \sqrt{-3}}{2}$と表します。
$\alpha,\,\omega\alpha,\,(\omega+1)\alpha$を複素数平面上に図示すると以下のようになります。
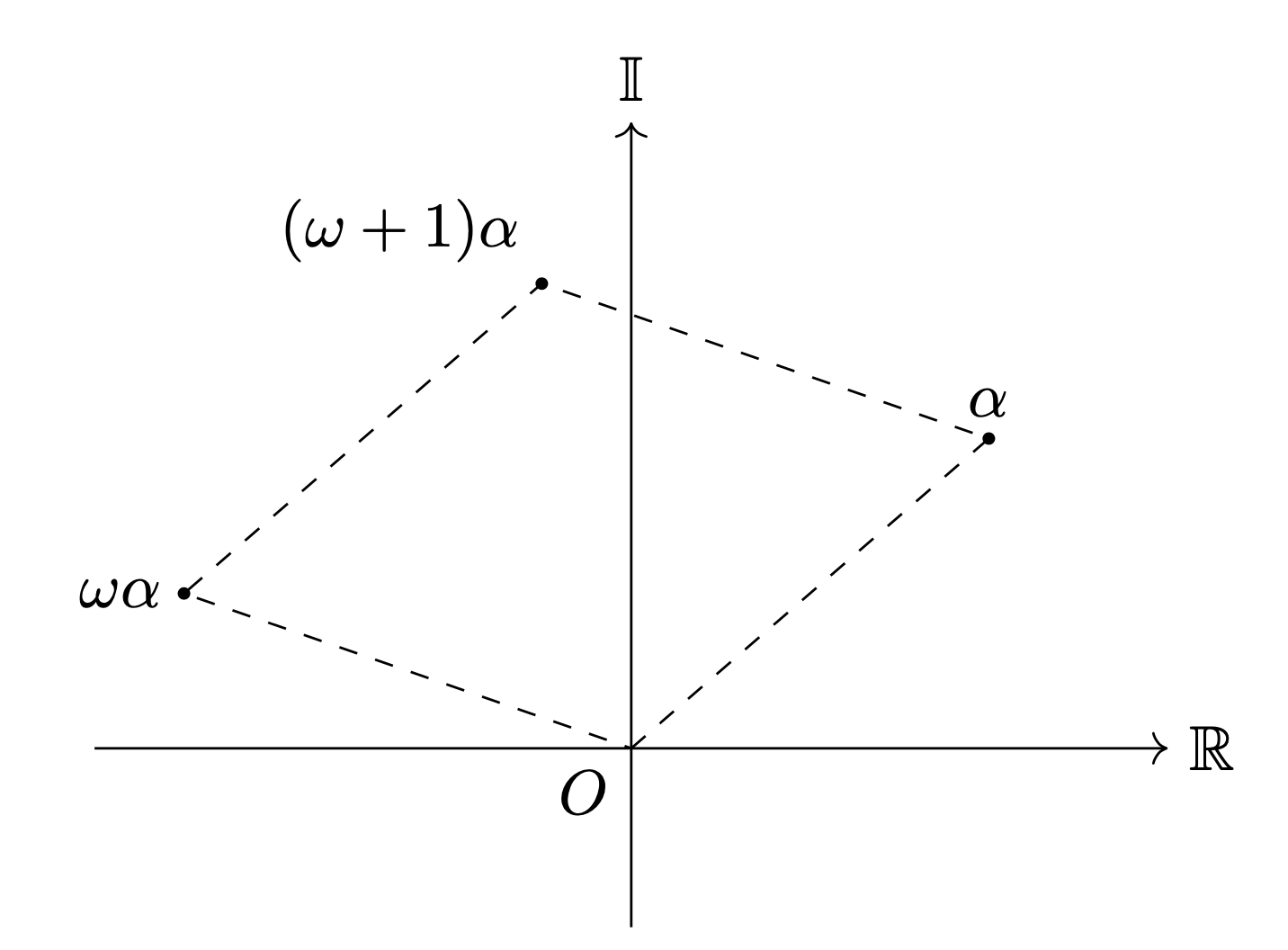
イデアル$I$の任意の元$\beta$は、$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の元$q,\,r$を適切に選ぶことで、
\[\beta=q\alpha+r(rは上図のひし形の内部または周上の点に対応する値)\]
と表せる。
なぜなら、$q=a+b\omega(a,\,b\in\mathbb{Z})$と表すとすると、$a$を1増やすことは、$r$を$-\alpha$だけ平行移動させることに対応し、$b$を1増やすことは$r$を$-\omega\alpha$だけ平行移動させることに対応するので、適切に$a,\,b$を増減させれば、この平行四辺形内に移動が可能だからです。
ひし形の$O$以外の頂点とちょうど$r$が一致した場合は、適切に$a,\,b$を増やすことで、$O$に対応させます。
このとき、$r$もイデアル$I$の元となるが、仮にひし形の内部または周上の点であって$O$以外の点に対応したと仮定すると、$|\alpha|$の最小性に反します。よって、平行移動した点は必ず$O$に一致することが分かります。
すなわち、イデアル$I$の任意の元$\beta$は、必ず$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の適切な元$q$を用いて、
\[\beta=q\alpha\]
の形で必ず表せることが分かったので、$I$は単項イデアルであることが示されました。
これを用いて、「イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでない」$\Leftrightarrow$「整数$a,\,b$を用いて、$p=a^2+ab+b^2$と表せる」を示します。
(証明)
1.「イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでない」$\Rightarrow$「整数$a,\,b$を用いて、$p=a^2+ab+b^2$と表せる」の証明
イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでないということは、
\[\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\supsetneq I\supsetneq p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\]
を満たすイデアル$I$が存在するということです。
$I$は上で証明した事実から単項イデアルであるので、$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の元の1つ$a-b\frac{-1+ \sqrt{-3}}{2}$を用いて、
\[I=\left(a-b\frac{-1+ \sqrt{-3}}{2}\right)\]
と表せます。
集合の包含関係から、$p$はイデアル$I$の元であり、$I$が単項イデアルであることも考慮すると、
\[p=\left(a-b\frac{-1+ \sqrt{-3}}{2}\right)\left(c-d\frac{-1+ \sqrt{-3}}{2}\right)\]
を満たす$c,\,d\in\mathbb{Z}$が存在します。
両辺の共役複素数をとると、
\[p=\left(a-b\frac{-1- \sqrt{-3}}{2}\right)\left(c-d\frac{-1- \sqrt{-3}}{2}\right)\]
これらを辺々かけると、
\[p^2=(a^2+ab+b^2)(c^2+cd+d^2)\]
ここで、
\[a^2+ab+b^2=\left(a+\frac{b}{2}\right)^2+\frac{3}{4}b^2\geqq 0\]
であり、同様にして$c^2+cd+d^2\geqq0$も分かるので、
\[(a^2+ab+b^2,\,c^2+cd+d^2)=(1,\,p^2),\,(p^2,\,1),\,(p,\,p)\]
の3通りが考えられる。
1-a. $(a^2+ab+b^2,\,c^2+cd+d^2)=(1,\,p^2)$のとき、
\[\left(a-b\tfrac{-1+ \sqrt{-3}}{2}\right)\left(a-b\tfrac{-1- \sqrt{-3}}{2}\right)=1\]
となります。ここで、
\[a-b\frac{-1- \sqrt{-3}}{2}=(a+b)+b\frac{-1+ \sqrt{-3}}{2}\left(\in\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\right)\]
であるので、$(a-b\frac{-1+ \sqrt{-3}}{2})(a-b\frac{-1- \sqrt{-3}}{2})$すなわち1は$I$の元だと分かります。
$1\in I$より、1と$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の元の積は全て$I$の元であるから、$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\subset I$が言えます。
しかし、これは$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\supsetneq I$に矛盾。
1-b.$(a^2+ab+b^2,\,c^2+cd+d^2)=(p^2,\,1)$のとき、
\[p=\left(a-b\tfrac{-1- \sqrt{-3}}{2}\right)\left(c-d\frac{-1- \sqrt{-3}}{2}\right)\]
の両辺に$\left(c-d\frac{-1- \sqrt{-3}}{2}\right)$をかけて、
\[p\left(c-d\tfrac{-1- \sqrt{-3}}{2}\right)=a-b\frac{-1+ \sqrt{-3}}{2}\]
ここで、$p\left(c-d\frac{-1- \sqrt{-3}}{2}\right)=p\{(c+d)+d\frac{-1+ \sqrt{-3}}{2}\}$は$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の元であるから、$a-b\frac{-1+ \sqrt{-3}}{2}$は$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の元であることが分かります。
したがって、
\[I=\left(a-b\tfrac{-1+ \sqrt{-3}}{2}\right)\subset p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\]
となるが、これは$I\supsetneq p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$に矛盾します。
以上より、
\[(a^2+ab+b^2,\,c^2+cd+d^2)=(p,\,p)\]
であるので、「イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでない」$\Rightarrow$「整数$a,\,b$を用いて、$p=a^2+ab+b^2$と表せる」が示されました。
2.「整数$a,\,b$を用いて、$p=a^2+ab+b^2$と表せる」$\Rightarrow$「イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでない」の証明
整数$a,\,b$を用いて、$p=a^2+ab+b^2$と表せるので、
\[p=\left(a-b\tfrac{-1+\sqrt{-3}}{2}\right)\left(a-b\tfrac{-1-\sqrt{-3}}{2}\right)\]
と因数分解できます。
このとき、$I=\left(a-b\frac{-1+\sqrt{-3}}{2}\right)$なる単項イデアル$I$を考えると、$p$はイデアル$I$の元となるので、$p$と$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の任意の元の積もイデアル$I$の元となります。すなわち、
\[I\supset p\mathbb{Z}\left[\tfrac{-1+ \sqrt{-3}}{2}\right]\]
が言えます。
また、$a,\,b$がともに$p$の倍数であったと仮定すると、$a^2+ab+b^2$は$p^2$の倍数となりますが、これは$p=a^2+ab+b^2$に矛盾するので、$a,\,b$のうち少なくとも一方は$p$の倍数でないです。つまり、$a-b\frac{-1+\sqrt{-3}}{2}$は$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の元ではありません。
したがって、
\[I\supsetneq p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\]
が言えます。
ここで、$I$が1を元に持つと仮定すると、
\[1=\left(a-b\frac{-1+ \sqrt{-3}}{2}\right)\left(c-d\frac{-1+ \sqrt{-3}}{2}\right)\]
をみたす$c,\,d$が存在することになります。
両辺の共役複素数をとると、
\[1=\left(a-b\frac{-1- \sqrt{-3}}{2}\right)\left(c-d\frac{-1- \sqrt{-3}}{2}\right)\]
これらを辺々かけて、
\[1=(a^2+ab+b^2)(c^2+cd+d^2)\]
となります。$a^2+ab+b^2 \geqq 0$かつ$c^2+cd+d^2\geqq0$であることも考慮すると、
\[a^2+ab+b^2=c^2+cd+d^2=1\]
が分かりますが、これは$p$が素数であることに矛盾します。
よって、$I$は1を元に持たず、
\[\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]\supsetneq I\]
であることが分かります。
したがって、「整数$a,\,b$を用いて、$p=a^2+ab+b^2$と表せる」$\Rightarrow$「イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでない」が示されました。
以上をまとめて、「イデアル$p\mathbb{Z}\left[\frac{-1+ \sqrt{-3}}{2}\right]$が可換環$\mathbb{Z}\left[\tfrac{-1+ \sqrt{-3}}{2}\right]$の極大イデアルでない」$\Leftrightarrow$「整数$a,\,b$を用いて、$p=a^2+ab+b^2$と表せる」が示されました。

