この記事を読むとわかること
・量子アルゴリズムの基礎知識
・ショアのアルゴリズムでなぜ素因数分解ができるか
・ショアのアルゴリズムで21を素因数分解するやり方
量子コンピューターやアルゴリズムについて学ぶなら、東大の授業でも教科書として使われている「量子コンピュータ入門」という本がおすすめです。
量子アルゴリズムの基礎知識
この記事ではショアのアルゴリズムを用いて21を素因数分解することを目標として、ショアのアルゴリズムに関わる部分についての量子アルゴリズムの基礎知識から説明していきます。
すでに量子アルゴリズムの基礎知識があるという方はこちら。
【量子アルゴリズムの基礎知識1】量子ビット
普通のパソコンにおいては、1ビットというのは0と1のどちらかの状態を取るものですが、量子コンピューターにおける量子ビットというのは、単位球面上の任意のベクトルを表せるものです。(実際に量子ビットがどのように実現されるかという話は抜きで、こういうものがあるという前提のもと話を進めていきます。)
1つの量子ビットの状態は、$|\alpha|^2+|\beta|^2=1$を満たす複素数$\alpha,\,\beta$と2つのベクトル$|0\rangle,\,|1\rangle$を用いて、
\[\alpha|0\rangle+\beta|1\rangle\]
と表されます。
これらの係数は観測確率を表しています。具体的には、量子ビットを観測すると$|\alpha|^2$の確率で$|0\rangle$の状態、$|\beta|^2$の確率で$|1\rangle$の状態だと観測されます。
複数の量子ビットを並べたもの(厳密にはエンタングル状態のもの)は、それらの積が1つのデータとなります。量子ビットの積は$\boldsymbol{\otimes}$という記号を使います。例えば、
\[\frac{|0\rangle+|1\rangle}{\sqrt{2}},\,\frac{1}{2}|0\rangle+\frac{\sqrt{3}}{2}i|1\rangle\]
という2つの量子ビットを並べたものは、
\[\begin{align*}&\frac{|0\rangle+|1\rangle}{\sqrt{2}}\otimes\left(\frac{1}{2}|0\rangle+\frac{\sqrt{3}}{2}i|1\rangle\right)\\=&\frac{1}{2\sqrt{2}}|0\rangle\otimes|0\rangle+\frac{\sqrt{3}i}{2\sqrt{2}}|0\rangle\otimes|1\rangle+\frac{1}{2\sqrt{2}}|1\rangle\otimes|0\rangle+\frac{\sqrt{3}i}{2\sqrt{2}}|1\rangle\otimes|1\rangle\end{align*}\]
となります。
ただ、毎回$|1\rangle\otimes|0\rangle$などと書くのは面倒ですよね。そこで、$|1\rangle\otimes|0\rangle$を$|1\rangle|0\rangle$と略記したりします。
さらに、これは2進数表示した数のように見ることもできるので、これを10進数表示に直して、$|2\rangle$と表したりもします。
この記事では、積の記号を省略した形以外に、量子ビットの積を10進数表示した書き方も用います。例えば、$|13\rangle$は、$|1\rangle|1\rangle|0\rangle|1\rangle$を表します。
量子アルゴリズムでは、この量子ビットを用いることで、一度に複数の計算を行うことができます。
量子コンピューターでは量子ビットを用いることで複数の計算を同時に行うことができる!
あまりイメージがわかないと思いますが、記事の後半で実際に素因数分解を行うところでわかると思います。
【量子アルゴリズムの基礎知識2】アダマールゲート
量子コンピューターには、量子ビットの状態を変化させる量子ゲートというものがあります。
量子ゲートには様々な種類がありますが、ショアのアルゴリズムでは、アダマールゲートというものだけ知っていれば大丈夫です。
アダマールゲートは、$|0\rangle$を$\frac{|0\rangle+|1\rangle}{\sqrt{2}}$に、$|1\rangle$を$\frac{|0\rangle-|1\rangle}{\sqrt{2}}$に変換させるものです。
アダマールゲートの役割
\[|0\rangle\rightarrow\frac{|0\rangle+|1\rangle}{\sqrt{2}}\]
\[|1\rangle\rightarrow\frac{|0\rangle-|1\rangle}{\sqrt{2}}\]
【量子アルゴリズムの基礎知識3】量子離散的フーリエ変換
基本的なゲートを複数組み合わせることで、量子状態に対して量子離散的フーリエ変換というものを施すことができます。量子離散的フーリエ変換は以下のような数式で表される変換です。
量子離散的フーリエ変換は、$n$量子ビットあるときに、$|j\rangle$というベクトルに対して、
\[|j\rangle\rightarrow \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{i\frac{2\pi kj}{2^n}}|k\rangle\]
という変換を施すものである。
また、この逆変換である逆量子離散的フーリエ変換は、$|j\rangle$というベクトルに対して、
\[|j\rangle\rightarrow \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{-i\frac{2\pi kj}{2^n}}|k\rangle\]
という変換を施すものである。
フーリエ変換がどのようなものか元々知っている方であれば、これらの式は見たことがあるはずです。実際、離散的フーリエ変換と数式はほぼ変わりません。
今回のショアのアルゴリズムにおいては逆量子離散的フーリエ変換を使うことになりますが、これは、周期の検出のために用いられます。詳しいことは、実際に因数分解をしてみるときに分かるでしょう。
【量子アルゴリズムの基礎知識4】コントロールビット
最後の基礎知識はコントロールビットというものです。コントロールビットは、ある処理を制御するビットのことを指し、コントロールビットが$1$のときはその処理が行われ、$0$のときは処理が行われないようになります。
コントロールビットは量子コンピューターに限らず、普通のコンピューターにもあるものですが、量子ビットの性質から、コントロールビットが$0$と$1$の重ね合わせ状態になっているので、コントロールビットの振る舞いも重ね合わせになっています。
例えば、$\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$の状態の量子ビットがコントロールビットであり、$|0\rangle$と$|1\rangle$を反転させるという処理を制御しているとすると、
\[\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes |0\rangle\rightarrow\frac{1}{\sqrt{2}}(|0\rangle|0\rangle+|1\rangle|1\rangle)\]
というように変化します。
ショアのアルゴリズムで21を因数分解してみる
さて、ショアのアルゴリズムを実際に用いて$21$を因数分解してみましょう!ショアのアルゴリズムは実は因数分解をするわけではなく、「位数」という特別な数を効率的に見つけるためのアルゴリズムです。位数とは厳密には群論の中で定義される用語ですが、ここでは以下のように理解しておけばOKです。
互いに素な2つの自然数$m,\,p$に対して、
\[m^r\equiv 1\,(\mathrm{mod} p)\]
を満たすような最小の自然数$r$のことを位数という。
今回、ショアのアルゴリズムによって$21$を因数分解する際には、$p=21$であり、また今回は$m$として$5$を採用します。
位数を見つけたあとにどうやって因数分解ができるかはあとで述べますが、実は位数が見つかれば高確率で因数分解が可能になります。
$m$として$5$を採用した場合に、位数を発見するまでの流れは以下のようになります。
ショアのアルゴリズムの流れ($n$ビット使う場合)
1.アダマールゲートを用いて$|0\rangle〜|2^n-1\rangle$までのすべてのベクトルの重ね合わせを作る
2.$21$と互いに素な自然数として$5$を選び、任意の$|y\rangle$に対し、
\[U|y\rangle=|5y(\mathrm{mod} 21)\rangle\]
なる演算を施す演算子$U$に対応するものを作用させることによって、$|5^0(\mathrm{mod} 21)\rangle〜|5^{2^n-1}(\mathrm{mod} 21)\rangle$をすべて計算する
3.逆量子離散フーリエ変換によって、位数の情報を取り出す
また、量子ビットの数は多ければ多いほどより精度よく位数を求めることができますが、多くなりすぎると手計算ではできなくなってしまうので,今回は4量子ビット(+4量子ビット)を使うことにします。
アダマールゲートで$|0\rangle〜|2^n-1\rangle$までのすべてのベクトルを作る
ショアのアルゴリズム全体の回路図は以下のようになります。ただし、一番下のビットは4ビット分をまとめて書いており、$|0\rangle〜|31\rangle$の状態までを取ることできます。
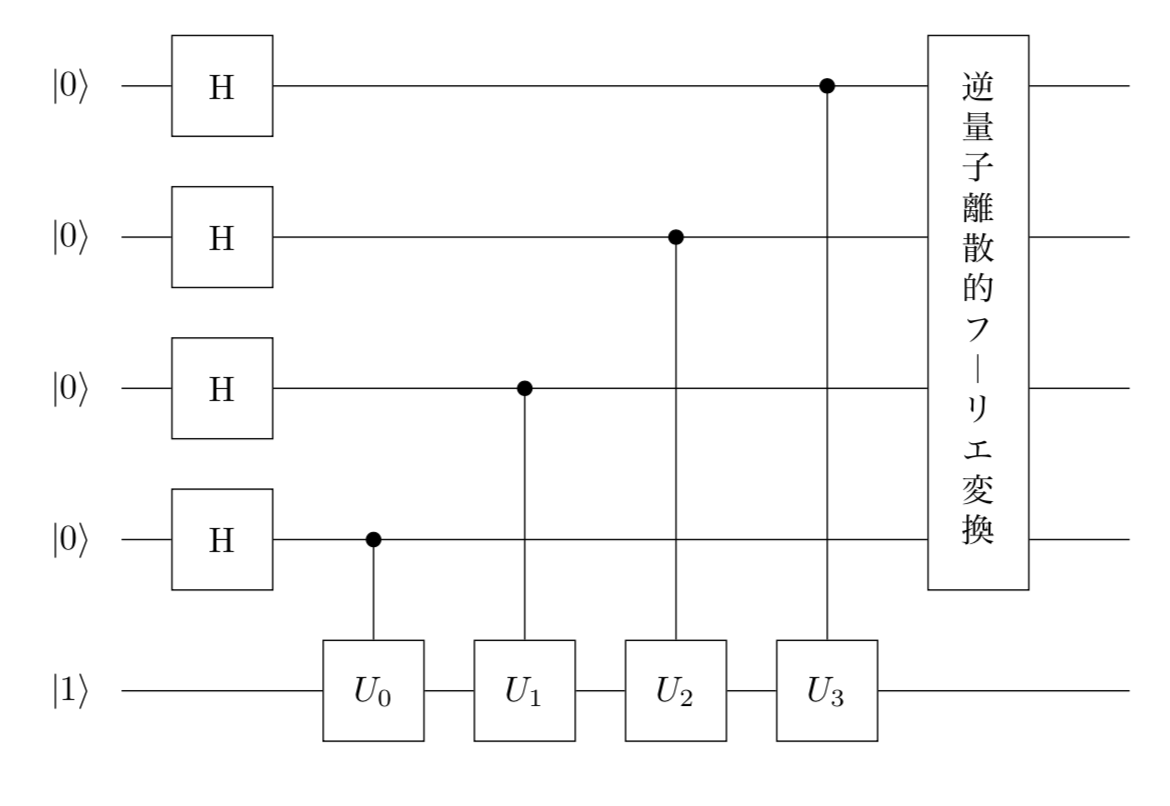
まず最初に$H$がたくさん並んでいるのがアダマールゲートです。回路全体の入力は$|0\rangle\otimes|0\rangle\otimes |0\rangle \otimes |0\rangle \otimes |1\rangle$であり、これらのうち0が並んでいる方にだけアダマールゲートが施されます。
実際に計算してみると、
\[\begin{align*}&\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes|1\rangle\\=&\frac{1}{4}(|0\rangle+|1\rangle)\otimes(|0\rangle+|1\rangle)\otimes(|0\rangle+|1\rangle)\otimes(|0\rangle+|1\rangle)\otimes|1\rangle\end{align*}\]
となります。このままだと0と1がただずらっと並んだだけにしか見えませんが、前半の4ビットに対してだけ10進数表示を用いれば、
\[\begin{align*}&\frac{1}{4}(|0\rangle+|1\rangle)\otimes(|0\rangle+|1\rangle)\otimes(|0\rangle+|1\rangle)\otimes(|0\rangle+|1\rangle)\\=&\frac{1}{4}\sum_{k=0}^{15}|k\rangle\end{align*}\]
となります。アダマールゲートのおかげで入力として$|0\rangle〜|2^n-1\rangle$までのすべてのベクトルの重ね合わせを作り出せたことが分かると思います。この入力の工夫が次に活きてきます。
$U|y\rangle=|5y(\mathrm{mod} 21)\rangle$なる$U$を作用させる
様々な数の重ね合わせが作り出せたら、次はそれをすべて$5$の指数部分にして,$5^0,\,5^1,\,5^2,\,\cdots,\,5^{15}$までをすべて計算します。
「そんなのどうやったらできるの?」と思いたくなりますが、$U|y\rangle=|5y(\mathrm{mod} 21)\rangle$という演算に対応する$U$を作り、それを図のように作用させると計算することができます。(ただし、$U_k$は$U^{2^k}$つまり、$U$を$2^k$回作用させたものを表します。)
図の中で・がいくつも並んでいますが、これは量子アルゴリズムの基礎で説明したコントロールビットを表しています。
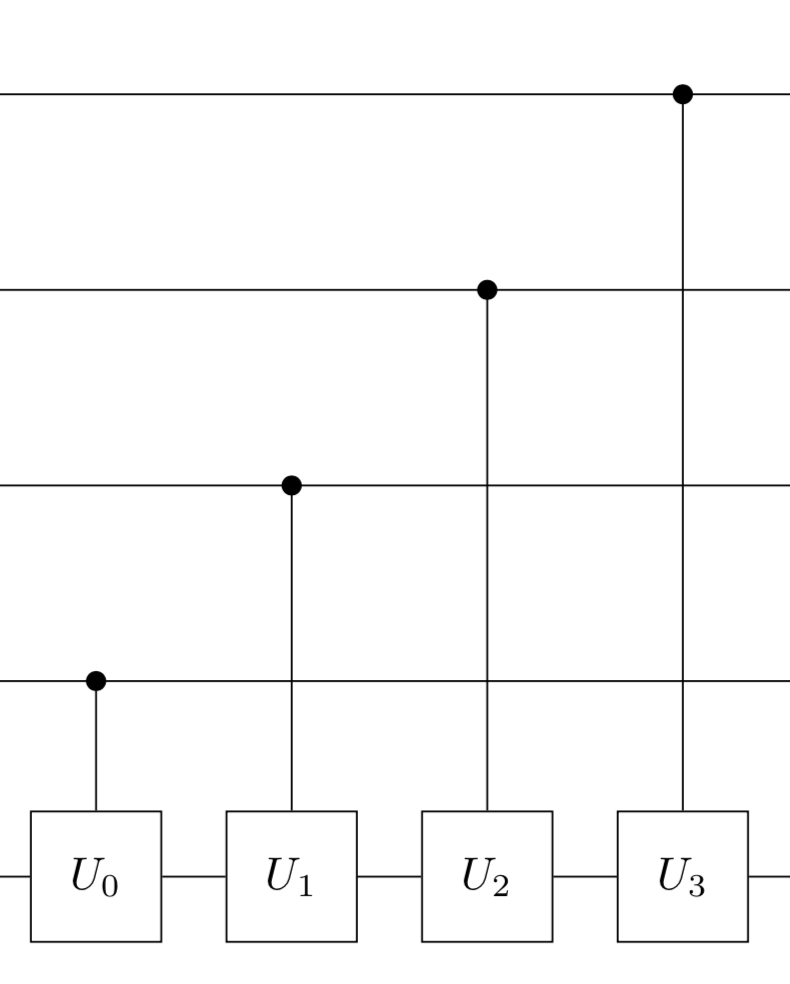
実際に計算して確かめてみましょう。
まず、4ビット目をコントロールビットとして、$U_0$を施して、
次に、3ビット目をコントロールビットとして、$U_1$を施して、
これを繰り返していって、最後に、1ビット目をコントロールビットとして、$U_3$を施して、
これは、上の4ビットと一番下のビットの積がたくさん出てきましたが、この計算過程も考えると、例えば
\[|6\rangle\otimes|1\rangle\]
であれば、$5^6$を$21$で割った余りが$1$になることを表しています。このように、$U$をうまく作用させたことによって、$5^0〜5^{15}$を$21$で割った余りをすべて計算することができました。
よって、式から位数は$6$であることが分かりますが、量子コンピューターではこの結果だけを取り出すことはできません。これは量子コンピューターを学ぶ上で非常に重要なことです。
量子ビットというのは、係数の絶対値の2上が観測される確率に対応する事を思い出すと、この計算が終わった段階で、右の出力がどうなっているかを観測すれば、
\[|0\rangle\otimes|1\rangle,\,|6\rangle\otimes|1\rangle,\,\cdots,\,|5\rangle\otimes|17\rangle,\,|11\rangle\otimes|17\rangle\]
の16個の状態を等確率で観測できるだけです。本来は因数分解するはずの合成数はとてつもなく大きな数で位数も非常に大きいですから、この状態を観測しても$|6\rangle\otimes|1\rangle$などの位数に関する情報が得られる状態を観測できる確率はほぼ0になります。よってここから、
量子コンピューターは一度に複数の計算を実行することができるが、個別の結果をすべてを取り出すことはできない!
ということが分かると思います。
では、ショアのアルゴリズムにおいてどうやって位数の情報を取り出すのでしょうか…?そこで出てくるのが逆量子離散的フーリエ変換です。
逆量子離散的フーリエ変換で位数の情報を取り出す
逆量子離散的フーリエ変換を施してあげると実は位数の情報を取り出すことができます。まず、ざっとした理解としては、「逆量子離散的フーリエ変換は周期を検出することができる変換」だと思っておけばよいでしょう。
位数というのは$5$のべき乗を$21$で割ったあまりがどのくらいの周期で変化するかというのと一致しているので、逆量子離散的フーリエ変換をすることによってその周期の情報を取り出すことができるのです。
はじめの4ビットに逆量子離散的フーリエ変換を施していきましょう。一番下の1ビットの出力が$|1\rangle$のときは、$|0\rangle+|6\rangle+|12\rangle$に逆量子離散的フーリエ変換を施して、
よって、4ビットの出力で観測される確率が極大になるのは$|0\rangle,\,|3\rangle,\,|5\rangle,\,|8\rangle,\,|11\rangle,\,|13\rangle$の近くです。同様にして、一番下の1ビットの出力が$|5\rangle$や$|17\rangle$のときなどの別の場合でも観測される確率が極大になるのは$|0\rangle,\,|3\rangle,\,|5\rangle,\,|8\rangle,\,|11\rangle,\,|13\rangle$の近くです。
実は、観測される確率が極大になるような$|m\rangle$は、$n$量子ビットを使ったとき、求めたい位数を$r$とすれば$\frac{2^n}{m}\simeq\frac{r}{k}(kは整数)$を満たすものです。
今回で言えば、
\[\frac{16}{m}\simeq \frac{6}{k}(kは整数)\]
となるような$|m\rangle$が観測される確率が極大になります。今回は、使っている量子ビットの数が少ないため、近似の精度が低くなってしまっていますが、もっと量子ビットを増やせばかなり精度の良い近似が得られて、$r$の情報が得やすくなります。
今回のように4量子ビットを使った場合には、
\[\frac{16}{3},\,\frac{16}{5},\,\frac{16}{8},\,\frac{16}{11},\,\frac{16}{13}\simeq \frac{r}{k}\]
となるので、何度も観測を繰り返して観測確率が極大になっているところを求めていけば、$\boldsymbol{r=6}$ではないかということがわかります。
これで晴れて位数を求めることができました!これは巨大な合成数についても全く同じようにできますよね。
逆量子離散的フーリエ変換によってなぜ位数がわかるのか
位数を見つけてあとは因数分解に繋げるだけですが、どうして先ほどのように
\[\frac{2^n}{m}\simeq\frac{r}{k}(kは整数)\]
を満たす時に観測確率が極大になるのでしょうか?
この点について、数学的な背景に少し踏み込んで説明していきます。興味のない方は読み飛ばしてもらって大丈夫です。
先ほどのように、演算子$U$を作用させていったあとには、位数$r$より小さい$0$以上の整数を$b$として
\[|b\rangle+|b+r\rangle+|b+2r\rangle\cdots \]
という形のベクトルが出てきます。これを逆量子離散的フーリエ変換するとどうなるかみてみましょう。
逆量子離散的フーリエ変換は、
\[|j\rangle\rightarrow \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{-i\frac{2\pi kj}{2^n}}|k\rangle\]
という変換でしたから、
\[\begin{align*}&|b\rangle\rightarrow \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{-i\frac{2\pi kb}{2^n}}|k\rangle\\&|b+r\rangle\rightarrow \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{-i\frac{2\pi k(b+r)}{2^n}}|k\rangle\\&\vdots\end{align*}\]
というように変換されていきます。
変換されたあとのベクトルを重ねていくと$|0\rangle〜|2^n-1\rangle$のベクトルの中で弱め合うベクトルと強め合うベクトルが出てくることに注目してください。強め合うベクトルというのはどのような条件を満たすものでしょうか?
強め合うようなベクトル$|m\rangle$は、同じ方向のベクトルが多数重なり合えばよいので、
\[\frac{2\pi mr}{2^n}\simeq 2k\pi\]
を満たすようなある整数$q$が存在しているものです。
これを整理すると、
\[\frac{2^n}{r}\simeq \frac{m}{k}\]
となり、先ほど出てきた条件式が得られました。十分大きな$n$について実験を行えば強め合いがよりはっきり現れることになります。
位数が求まったあとの因数分解のやり方
位数が求まってから、これを因数分解に応用します!ここからは、量子アルゴリズムは関係なく、ただの数学ですね。ポイントは3つあります。
量子アルゴリズムで位数が求まったあとの手順!
1.位数が偶数でなければやり直し
2.$m^{偶数}\equiv 1\Leftrightarrow \left(m^{\frac{偶数}{2}}-1\right)\left(m^{\frac{偶数}{2}}+1\right)\equiv 0$とユークリッドの互除法を用いる
3.うまくいかなければやり直し
これらについてそれぞれ説明していきます。
位数が偶数でなければやり直し
量子アルゴリズムを用いて計算してみたものの、位数として偶数でないものが出てきてしまった場合にはやり直しをすることになります。これは、次の項で説明するような合同式の変形が位数が偶数のときしかできないことが理由になります。
最初に、位数を求めることが目的だと言いましたが、正確には「偶数の位数を求めることが目的」ということになります。
上の例では$21$に互いに素な数として$5$を適当に選びましたが、たまたま$6$という偶数の位数が求まったのでラッキーですね!
$m^{偶数}\equiv 1\Leftrightarrow \left(m^{\frac{偶数}{2}}-1\right)\left(m^{\frac{偶数}{2}}+1\right)\equiv 0$と互除法を利用
中学校の数学で、
\[x^2-1=(x+1)(x-1)\]
という因数分解を習ったことがあると思いますが、それと同じく、
\[m^{偶数}\equiv 1\Leftrightarrow \left(m^{\frac{偶数}{2}}-1\right)\left(m^{\frac{偶数}{2}}+1\right)\equiv 0\]
が成り立ちますよね。
そこで、偶数の位数が求まったら、位数の定義から、因数分解をしたい合成数を法として、
\[m^{位数}\equiv 1\Leftrightarrow \left(m^{\frac{位数}{2}}-1\right)\left(m^{\frac{位数}{2}}+1\right)\equiv 0\]
が言えます。そこで、
\[m^{\frac{位数}{2}}-1,\,m^{\frac{位数}{2}}+1\]
の2つの数と元の合成数とでそれぞれユークリッドの互除法を使ってあげれば、元の合成数の素因数がこれらの2つの整数に散らばっている可能性があります。あくまでこれは可能性であって、本当に素因数が2つの数に散らばったかどうかがわからないところが注意点です。
$21$の場合は、
\[5^{6}\equiv 1\Leftrightarrow (5^{3}-1)(5^3+1)\equiv 0\]
となるので、$124$と$126$という数についてそれぞれ$21$とユークリッドの互除法をおこなってあげればOKです。
しかしながら、
\[126=21\times 6\]
\[124=21\times 5+19\]
となるので、「$21$の倍数」と「$21$に互いに素な数」の積が出てきただけでした…
というわけで、このままだと因数分解ができません!
ではこういう場合にはどうするんでしょうか…?
うまくいかなければやり直し
$5$を選んだ場合のように上手く行かなければ、素因数分解したい数字に互いに素な自然数を改めて選び直して、再びショアのアルゴリズムを実行することになります。
「こんなに長々と説明してきたのに結局やり直しなの!」と思ってしまいますが、これはしょうがないことですね。
例えば、$21$に互いに素な数として$2$を選び直すと、位数として$6$が求まり、
\[(2^3-1)(2^3+1)\equiv 0\]
となるので、$7,\, 9$が得られます。それぞれについて$21$とユークリッドの互除法を用いると、約数として$3,\,7$が求まるので晴れて因数分解ができました!
ショアのアルゴリズムではこのようにして、
因数分解したい合成数と互いに素な数を選んでから位数を計算→偶数の位数が求まったら合同式を変形してユークリッドの互除法を用いてみる→うまくいけば約数が求まる!(うまくいかなければ数字の選び直し!)
という流れになっていることがわかったと思います。
まとめ
・ショアのアルゴリズムは偶数の位数を効率的に求めるためのアルゴリズム
・量子ビットを用いることによってあらゆる整数乗の計算を一気に行うことができる
・逆量子離散的フーリエ変換を行って確率の強め合いを起こして位数の情報を取り出す
・偶数の位数が求まったら合同式の変形とユークリッドの互除法を用いて上手く行けば約数が分かる
・うまくいかなければ何度も計算をし直さないといけない!

