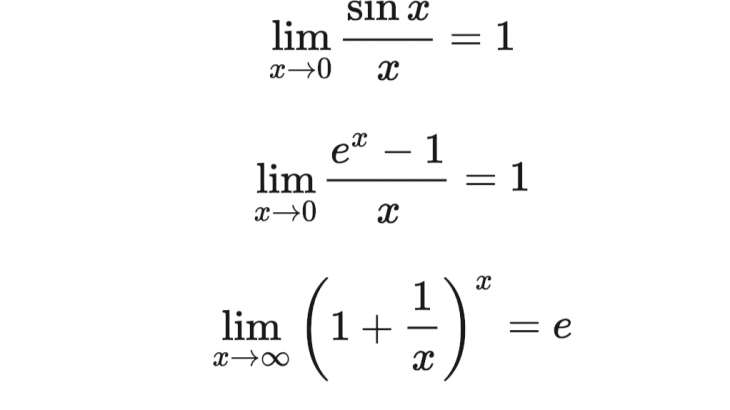この記事を読むとわかること
\[\lim_{x\to 0}\frac{\sin{x}}{x}=1\]
\[\lim_{x\to \infty}\frac{\sin{x}}{x}=0\]
・sinx/xの極限の証明
・sinx/xの極限を高校数学の範囲内で循環論法にならずに証明する方法
lim(x→0)sinx/xの極限値は?
$\lim_{x\to 0}\frac{\sin{x}}{x}=1$になる
$\lim_{x\to 0}\frac{\sin{x}}{x}$の値は$1$になります。
この事実は、極限計算の時に用いるだけでなく、$\sin{x}$や$\cos{x}$などの三角関数の微分を導出する際にも用いるので非常に重要です。
では、
\[\lim_{x\to 0}\frac{\sin{x}}{x}=1\]
となることはどのように証明するのでしょうか?
$\lim_{x\to 0}\frac{\sin{x}}{x}=1$の証明
証明は以下のようになります。
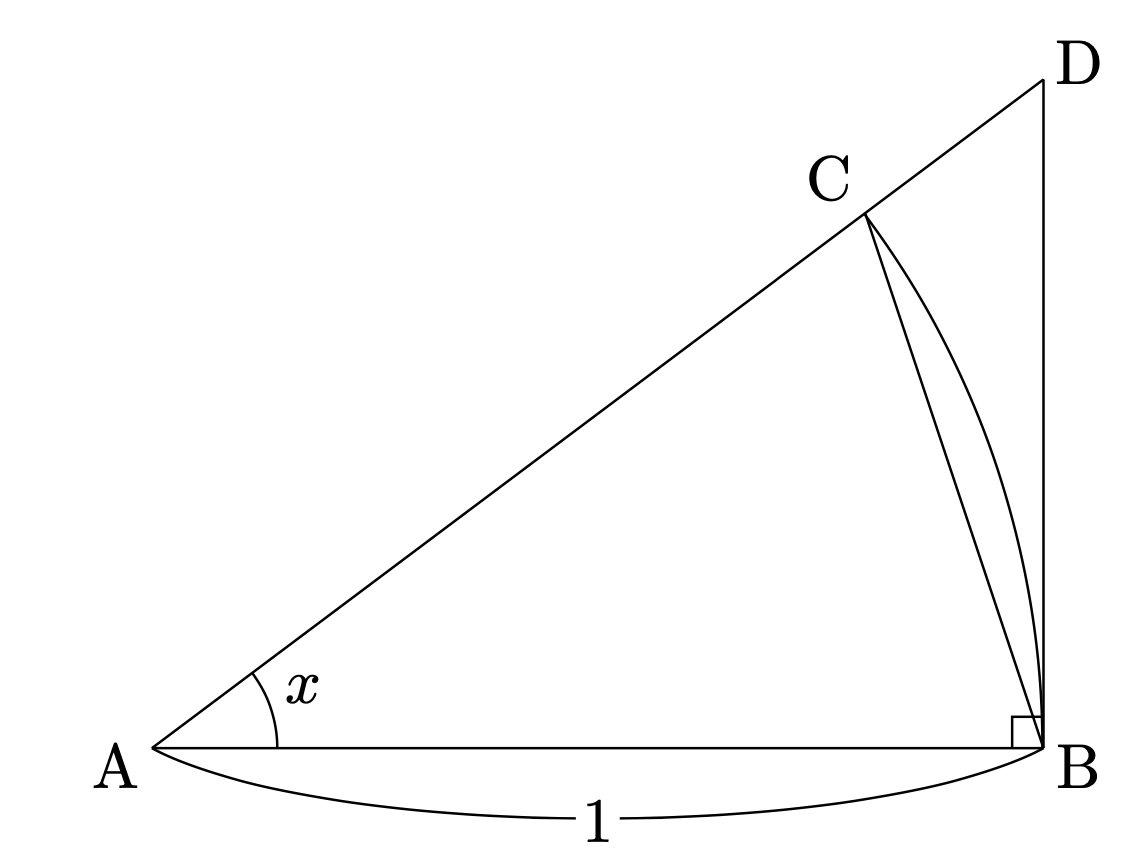
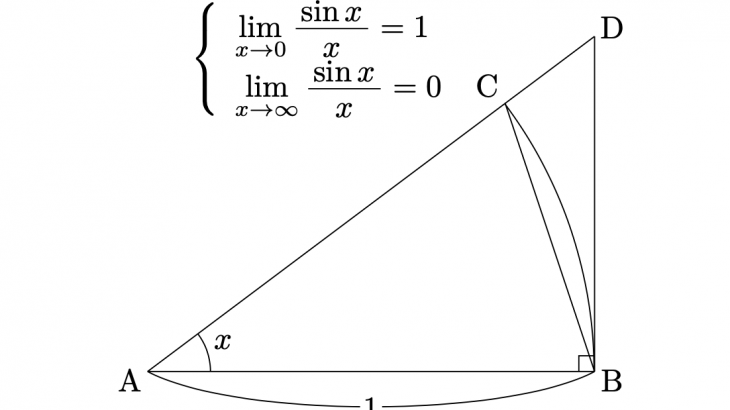
上図より、$0<x<\frac{\pi}{2}$において、
\[\triangle\mathrm{ABC}の面積<扇形の面積<\triangle\mathrm{ABD}の面積\]
という関係が成り立つから、
\[\frac{1}{2}\sin{x}<\frac{1}{2}x<\frac{1}{2}\tan{x}\]
が成り立つ。よって、$x>0$に注意して変形すると、
\[\cos{x}<\frac{\sin{x}}{x}<1\]
となる。また、
\[\lim_{x\to +0}\cos{x}=1\]
であるので、はさみうちの定理から、
\[\lim_{x\to +0}\frac{\sin{x}}{x}=1\]
がわかる。さらに、
\[\frac{\sin{x}}{x}=\frac{\sin{(-x)}}{-x}\]
であることより、
\[\lim_{x\to -0}\frac{\sin{x}}{x}=1\]
も言える。したがって、
\[\lim_{x\to 0}\frac{\sin{x}}{x}=1\]
が示された。
全体の流れとしては、図形的な性質が使える$x>0$の場合において、はさみうちの定理を用いて極限値を求め、$\frac{\sin{x}}{x}$が偶関数であるという性質を使って$x<0$の場合も示せるという感じになっています。
lim(x→∞)sinx/xの極限値は?
$x\to 0$の場合を説明しましたが、$x\to\infty$の場合の極限値はどうなるのでしょうか?
lim(x→∞)sinx/x=0になる
$\lim_{x\to \infty}\frac{\sin{x}}{x}$の値は$0$になります。
こちらは、先ほどと違ってあまり重要な結果ではありません。学校のテストでひっかけ問題として出題されるくらいではないでしょうか。
これも証明しましょう。
lim(x→∞)sinx/x=0の証明
証明は以下のようになります。
任意の実数$x$に対して、$0\leqq|\sin{x}|\leqq 1$が成り立ち、
\[\lim_{x\to\infty}\frac{1}{x}=0\]
であるので、はさみうちの定理から、
\[\lim_{x\to\infty}\left|\frac{\sin{x}}{x}\right|=0\]
が言える。したがって、
\[\lim_{x\to \infty}\frac{\sin{x}}{x}=0\]
分母である$x$は大きくなっていくにも関わらず、$\sin{x}$は$-1$と$1$の間を周期的に動くだけなので、$0$に収束することは即座にわかります。そこで、はさみうちの定理を用いてあげればよさそうです。
上の証明のように絶対値付きで$0$に収束するという証明の流れにしておく必要性はありませんが、
\[\frac{-1}{x}<\sin{x}<\frac{1}{x}\]
という不等式を書いた場合には、これが成り立つのは$x>0$のときであって、任意の実数では成り立たないことに注意しましょう。
lim(x→0)sinx/x=1の証明は循環論法って本当?
進学校に通われている方なら、学校の授業で、
\[\boldsymbol{\lim_{x\to 0}\frac{\sin{x}}{x}=1}\]
の証明は循環論法で、高校数学では実は証明できないという話をされたことがあるかと思います。
循環論法というのは、ある事柄を証明するときに、その事柄を正しいと仮定して話をしてしまっていることを意味します。
上の証明のどこが循環論法なのでしょうか?
まず、
$\lim_{x\to 0}\frac{\sin{x}}{x}=1$
を証明するときには、扇形の面積が$\frac{1}{2}x$であることを用いています。扇形の面積の公式は、円の関数の積分によって求めます。
例えば、$x$軸よりも上側の場合は、円の方程式は、
\[y=\sqrt{1-x^2}\]
で表されるので、これを積分するには、$x=\cos{t}$などと置換して積分することになります。
このように、三角関数で置換したときには、
\[\frac{dx}{dt}=-\sin{t}\]
というように、三角関数の微分が必要になり、また、置換したあとに積分を実行する際にも、三角関数の微分の知識を使うことになります。
三角関数の微分を証明するときには、
$\lim_{x\to 0}\frac{\sin{x}}{x}=1$
であることを使います。
つまり、図にすると以下のような循環論法になっているわけです。
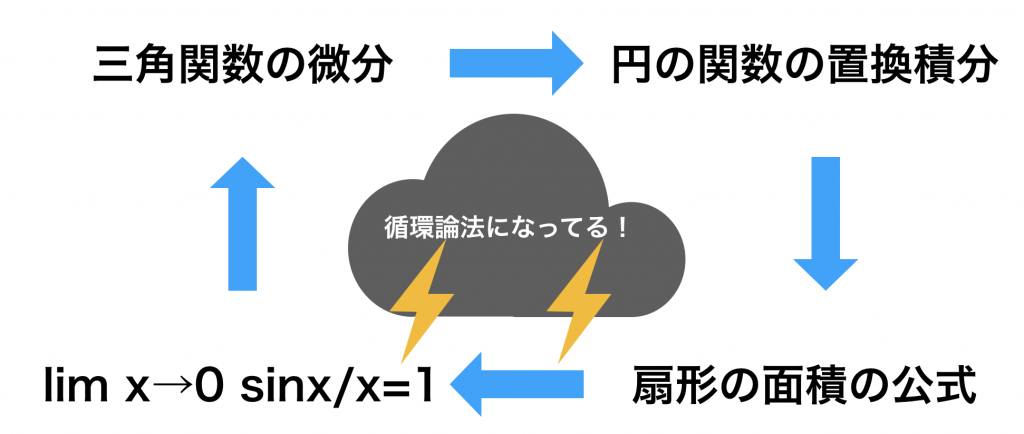
では、極限の公式を本当の意味で証明をすることはできないのでしょうか…?
循環論法にならずに証明は可能
結論から言うと、循環論法にならずに、この極限の公式を証明することは可能です!しかも、高校数学の範囲内で証明をすることが可能です。
循環論法にならないための大事なポイントは以下の3点です。
\[\lim_{x\to 0}\frac{\sin{x}}{x}=1\]
を循環論法にならずに証明するためのポイント2つ!
・置換積分をせずに部分積分をする
・円弧の長さを積分によって定義する
詳しく説明していきましょう。
扇形の面積を求めるときに置換積分ではなく部分積分をする
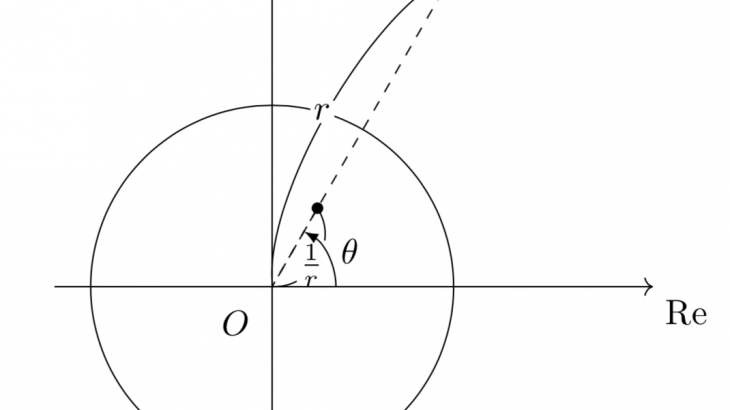
扇形の面積を求める際に、三角関数で置換するという状況を変えることがスタートポイントになります。下図のような扇形の面積を求めるのを考えましょう。
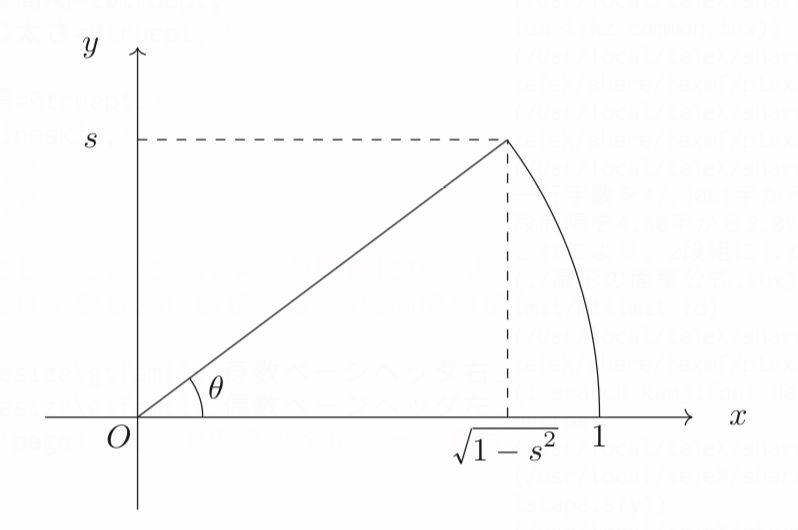
これは、積分を使って表せば、
\[\int_{0}^{s}\sqrt{1-y^2}dy-\frac{1}{2}s\sqrt{1-s^2}\]
となりますね。(積分したものから三角形を除く計算をしています。)
この積分の部分を計算するときに三角関数によって置換をするのが問題の発端です。ここで、
\[\begin{align*}\int_{0}^{s}\sqrt{1-y^2}dy=&\int_{0}^{s}(y)^{\prime}\sqrt{1-y^2}dy\\=&\left[y\sqrt{1-y^2}\right]^{s}_{0}+\int_{0}^{s}\frac{y^2}{\sqrt{1-y^2}}dy\\=&s\sqrt{1-s^2}+\int_{0}^{s}\frac{y^2}{\sqrt{1-y^2}}dy\end{align*}\]
というように、部分積分を一回挟んであげることによって、実は三角関数による置換積分を避けられるようになります。
積分の形になっている部分について、さらに変形を進めると、
\[\begin{align*}&\int_{0}^{s}\frac{(y^2-1)+1}{\sqrt{1-y^2}}dy\\=&-\int_{0}^{s}\sqrt{1-y^2}dy+\int_{0}^{s}\frac{1}{\sqrt{1-y^2}}dy\end{align*}\]
となるので、以上の議論をまとめると、$I=\int_{0}^{s}\sqrt{1-y^2}dy$とおけば、
\[\begin{align*}&I=s\sqrt{1-s^2}-I+\int_{0}^{s}\frac{1}{\sqrt{1-y^2}}dy\\\Leftrightarrow &I=\frac{1}{2}s\sqrt{1-s^2}+\frac{1}{2}\int_{0}^{s}\frac{1}{\sqrt{1-y^2}}dy\end{align*}\]
となるので、結局、
\[\int_{0}^{s}\frac{1}{\sqrt{1-y^2}}dy\]
が求まれば扇形の面積が求まるわけです。
円弧の長さを積分によって求める
小学校の頃から、円弧の長さは半径と中心角の大きさによって求めるように教えられてきたと思いますが、ここで、円弧の長さを積分によって求めるという作業を行います。
円弧の長さは、$x=\sqrt{1-y^2}$に対して、
\[\int_{0}^{s}\sqrt{1+\left(\frac{dx}{dy}\right)^2}dy\]
と表されるので、
\[\frac{dx}{dy}=-\frac{y}{\sqrt{1-y^2}}\]
であることも合わせると、円弧の長さは、
\[\int_{0}^{s}\sqrt{1+\frac{y^2}{1-y^2}}dy=\int_{0}^{s}\frac{1}{\sqrt{1-y^2}}dy\]
となります。
つまり、先ほどの議論ででてきた、求めたい積分というのは、円弧の長さを表しているものと全く同じだということが分かります。円弧の長さは半径と中心角の積にも一致するので、$s=\sin{\theta}$なる角度$\theta(0<\theta<\frac{\pi}{2})$を定めれば、
\[I=\frac{1}{2}s\sqrt{1-s^2}+\frac{1}{2}\theta\]
と求めることができました。
したがって、扇形の面積は、
\[\frac{1}{2}s\sqrt{1-s^2}+\frac{1}{2}\theta-\frac{1}{2}s\sqrt{1-s^2}=\frac{1}{2}\theta\]
と分かりました。
以上の議論で、三角関数の微分や積分は一切出てきていないですよね?このようにして循環論法から抜け出すことができます。
まとめ
\[\lim_{x\to 0}\frac{\sin{x}}{x}=1\]
\[\lim_{x\to \infty}\frac{\sin{x}}{x}=0\]
・sinx/xの極限が1になることは部分積分を使えば循環論法にならずに証明できる!