東大医学部生の相談室

解の配置問題のパターンや解き方を例題付きで東大医学部生が解説！

この記事を読むとわかること

・解の配置問題のパターン

・各パターンに対応した例題とその解き方

・解の配置問題の実際の解答

解の配置問題のパターン一覧

解の配置問題とは、定められた範囲に決められた数だけ方程式が実数解を持つための条件を求める問題です。解の配置問題の典型的な問題のパターンには以下の4種類があります。

解の配置問題の4パターン

・ある範囲に異なる2実数解を持つ

・ある範囲にただ1つの実数解を持つ

・ある範囲に少なくとも1つの実数解を持つ

・3次以上の方程式の場合

まず、解の配置問題を解くための一般論を紹介してから、これらのパターンそれぞれに対応した例題とその解答を載せていきます。

解の配置問題の解き方

解の配置問題は方程式ではなくグラフの問題と見る

解の配置問題を解く上で最も重要な事項として、方程式の問題に見えますが、解くときにはグラフがxx軸のどこと共有点を持つのかについて考える問題として捉えます。

解の配置問題ではグラフを考える！

よって、方程式が与えられたら、y=(左辺)y=(\text{左辺})というグラフを考えて、どのような条件を満たせばよいのか考えていくことになります。

2次関数のはじき(判別式・軸・境界(端点))を考える！

2次方程式の解の配置問題の場合は2次関数を考えることになりますが、解の存在範囲を考えるときには、方程式の判別式と軸の位置、範囲の端点(境界)の正負を考えるだけで十分であることがほとんどです。

 

小学校の頃に、速さ×時間=距離、という公式を習う際に、それぞれの頭文字を取って「はじき」と覚えると習った方もいると思います。

2次方程式の解の配置の時に考えるものも、2次関数の判別式、軸、境界(端点)の3つであるため、「はじき」と同じ語呂合わせで覚えることができますね。

3次以上の関数であれば定数分離をする

3次以上の関数の場合は、判別式や軸を考えることはできないので、あまり複雑な解の配置問題を出題することはできません。そのため、文字定数が含まれていて、定数分離をし、3次関数との共有点の変化を見やすくしてあげることで解決することが多いです。

解の配置問題に限らず、高次方程式の解について考えるときに文字定数が含まれていたら定数分離するという鉄則があります。

高次方程式の解について考えるときに、文字定数が含まれていたら定数分離する！

 

定数分離についてはこちらの記事に詳しく書いてあります。

関連記事 定数分離とは？使い方や使える条件、応用問題まで解説します！

解の公式を考えて不等式を解くのはダメ！

解の配置問題の経験が浅い受験生は、ついつい方程式の解を解の公式によって求めて、不等式を解こうとしてしまいがちですが、解の公式を使うのは絶対にやめましょう。なぜなら、解の公式ででてきた汚い式が含まれた不等式をミスなく同値変形して計算していくのは至難の技だからです。

解の配置問題で解の公式を使うのはNG！！

必ず、判別式、軸、端点の3つを考えて解くようにしましょう。

解と係数の関係を使って解けるときもあるが非推奨

解の配置問題を解く時に、解と係数の関係を上手く使って解ける場合もありますが、これもミスが増える原因になるのでやめておくべきでしょう。

たとえば、2解が00以上11以下の範囲に入っているための条件を求めるときに、2解をα, β\alpha,\,\betaとして、

{0≦α≦10≦β≦1⇔{0≦α+β≦20≦αβ≦1\left\{\begin{array}{l}0\leqq \alpha \leqq 1\\0\leqq \beta \leqq 1\end{array}\right.\Leftrightarrow\left\{\begin{array}{l}0\leqq \alpha+\beta \leqq 2\\0\leqq \alpha\beta \leqq 1\end{array}\right.

と変形してしまうミスなどが非常によく見られます。

これは、図を描いてみれば、明らかに同値でないことがわかると思います。解と係数の関係を用いて条件を言い換えようとするとミスする方が多いので、基本に忠実に判別式、軸、端点を考えていきましょう。

解の配置問題の解答

上で挙げた4つのパターンに対応した例題とその解答、解説を載せていきます。

問題1

xxの2次方程式

x2+ax+a2−3=0x^2+ax+a^2-3=0

が−1<x<2-1<x<2の範囲に相異なる2つの実数解を持つための実数aaの条件を求めよ。

解答

x2+ax+a2−3=(x+a2)2+34a2−3x^2+ax+a^2-3=\left(x+\frac{a}{2}\right)^2+\frac{3}{4}a^2-3

であるから、与えられた方程式の左辺をf(x)f(x)とおくと、y=f(x)y=f(x)の軸はx=−fraca2x=-frac{a}{2}また、f(x)=0f(x)=0の判別式をDDとすると、求める条件は、

{D>0−1<−a2<2f(−1)>0f(2)>0⇔{a2−4(a2−3)>0−4<a<2a2−a−2>0a2+2a+1>0⇔{−2<a<2−4<a<2a<−1, 2<aa≠−1⇔−2<a<−1\begin{align*}&\left\{\begin{array}{l}D>0\\-1< -\frac{a}{2} <2 \\f(-1)>0\\f(2)>0\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}a^2-4(a^2-3)>0\\-4< a < 2\\a^2-a-2>0\\a^2+2a+1>0\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}-2<a<2\\-4< a <2\\a<-1,\,2<a\\a\ne -1\end{array}\right.\\\Leftrightarrow &\boldsymbol{-2<a<-1}\end{align*}

解説

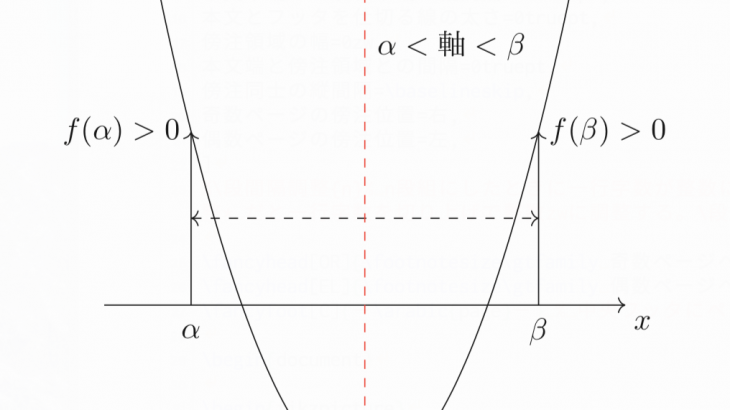
与えられた範囲がα<x<β\alpha <x<\betaだとしたとき、下図のようになっていればその範囲に相異なる2つの実数解を持っていますよね。

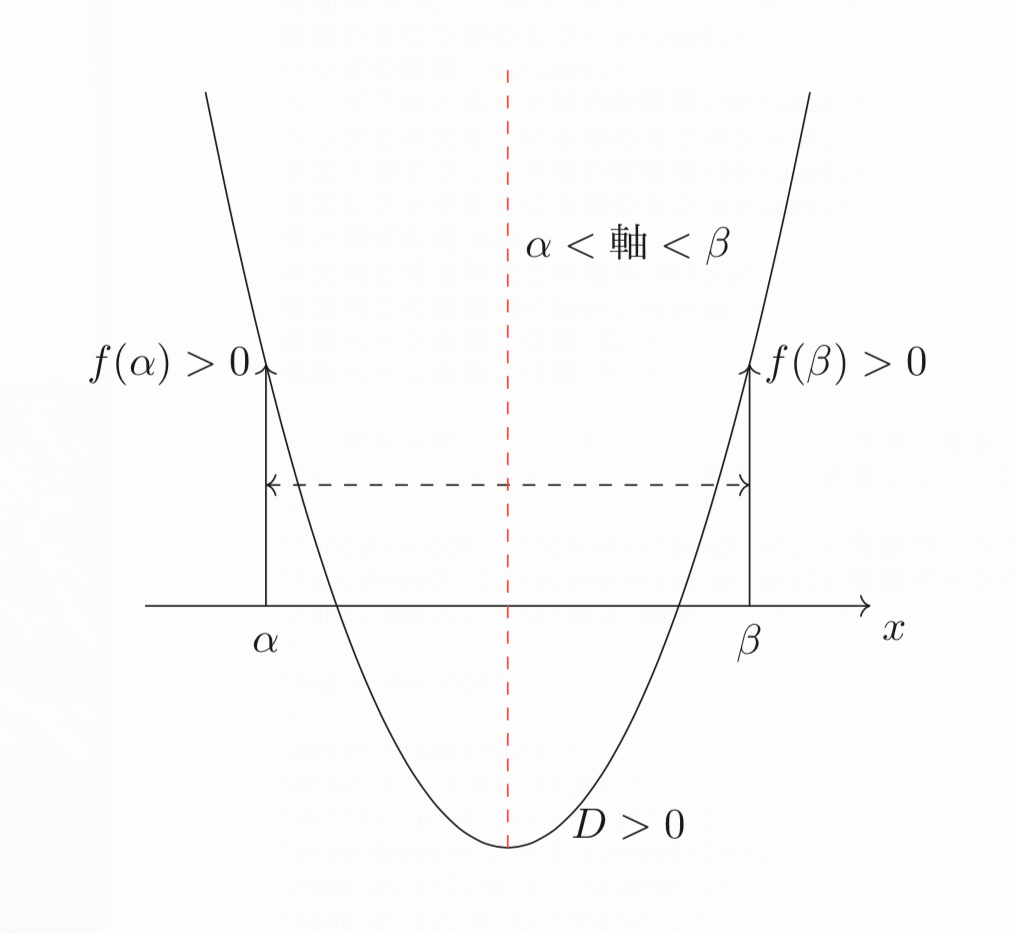
2次方程式f(x)=0f(x)=0がα<x<β\alpha <x<\betaという範囲に相異なる2つの実数解を持つときの条件は、

{D>0α<軸<βf(α)>0f(β)>0\left\{\begin{array}{l}D>0\\\alpha<\text{軸}<\beta\\f(\alpha)>0\\f(\beta)>0\end{array}\right.

※与えられた範囲の端に等号がついていていてα≦x≦β\alpha\leqq x\leqq \beta となっていた場合は、

{D>0α≦軸≦βf(α)≧0f(β)≧0\left\{\begin{array}{l}D>0\\\alpha\leqq \text{軸}\leqq\beta\\f(\alpha)\geqq0\\f(\beta)\geqq0\end{array}\right.

とすればOKです。

 

さて、求めた答えが合っているか、視覚的に確かめてみましょう。aaを−52≦a≦−12-\frac{5}{2}\leqq a\leqq -\frac{1}{2}の範囲で動かしたときには、以下の動画のようになります。

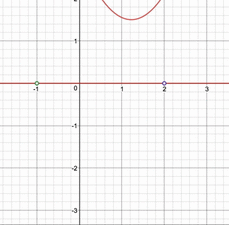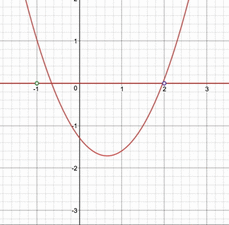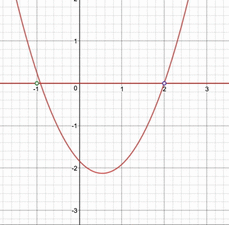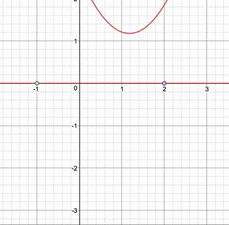
aaが−2-2以下になると相異なる2つの実数解を持つという条件が満たされなくなり、−1-1以上になると実数解のうちの小さい方が−1-1以下になってしまうことが見てわかると思います。

問題2

xxの2次方程式

x2+2ax−a+1=0x^2+2ax-a+1=0

が−1<x<3-1<x<3の範囲にただ1つの実数解を持つための実数aaの条件を求めよ。(重解の場合もただ1つの実数解の場合に含む)

解答

x2+2ax−a+1=(x+a)2−a2−a+1x^2+2ax-a+1=(x+a)^2-a^2-a+1

であるから、与えられた式の左辺をf(x)f(x)とおくと、y=f(x)y=f(x)の軸は、x=−ax=-aまた、f(x)=0f(x)=0の判別式をDDとおく。(i)f(x)=0f(x)=0がx=−1x=-1またはx=3x=3を解に持つとき、

f(−1)=0⇔a=23f(-1)=0\Leftrightarrow a=\frac{2}{3}

f(3)=0⇔a=−2f(3)=0\Leftrightarrow a=-2

であり、a=23a=\frac{2}{3}のとき、

x2+43+13=0⇔x=−13, −1x^2+\frac{4}{3}+\frac{1}{3}=0\Leftrightarrow x=-\frac{1}{3},\,-1

より適する。a=−2a=-2のとき、

x2−4x+3=0⇔x=1, 3x^2-4x+3=0\Leftrightarrow x=1,\,3

より、適する。(ii)f(x)=0f(x)=0がx=−1, 3x=-1,\,3を解に持たないとき、題意を満たすのは、

{D=0−1<−a<3またはf(−1)f(3)<0⇔{a2+a−1=0−3<a<1または(2−3a)(5a+10)<0⇔a=−1±52, a<−2, 23<a\begin{align*}&\left\{\begin{array}{l}D=0\\-1<-a<3\end{array}\right.\text{または}f(-1)f(3)<0\\\Leftrightarrow&\left\{\begin{array}{l}a^2+a-1=0\\-3<a<1\end{array}\right.\text{または}(2-3a)(5a+10)<0\\\Leftrightarrow&a=\frac{-1\pm\sqrt{5}}{2},\,a<-2,\,\frac{2}{3}<a\end{align*}

のとき。

以上より、求める条件は、

a≦−2, a=−1±52, 23≦a\boldsymbol{a\leqq-2,\,a=\frac{-1\pm\sqrt{5}}{2},\,\frac{2}{3}\leqq a}

解説

与えられた範囲がα<x<β\alpha <x<\betaだとしたとき、下図のようになっていればその範囲にただ1つの実数解を持つのはすぐに思いつくと思います。

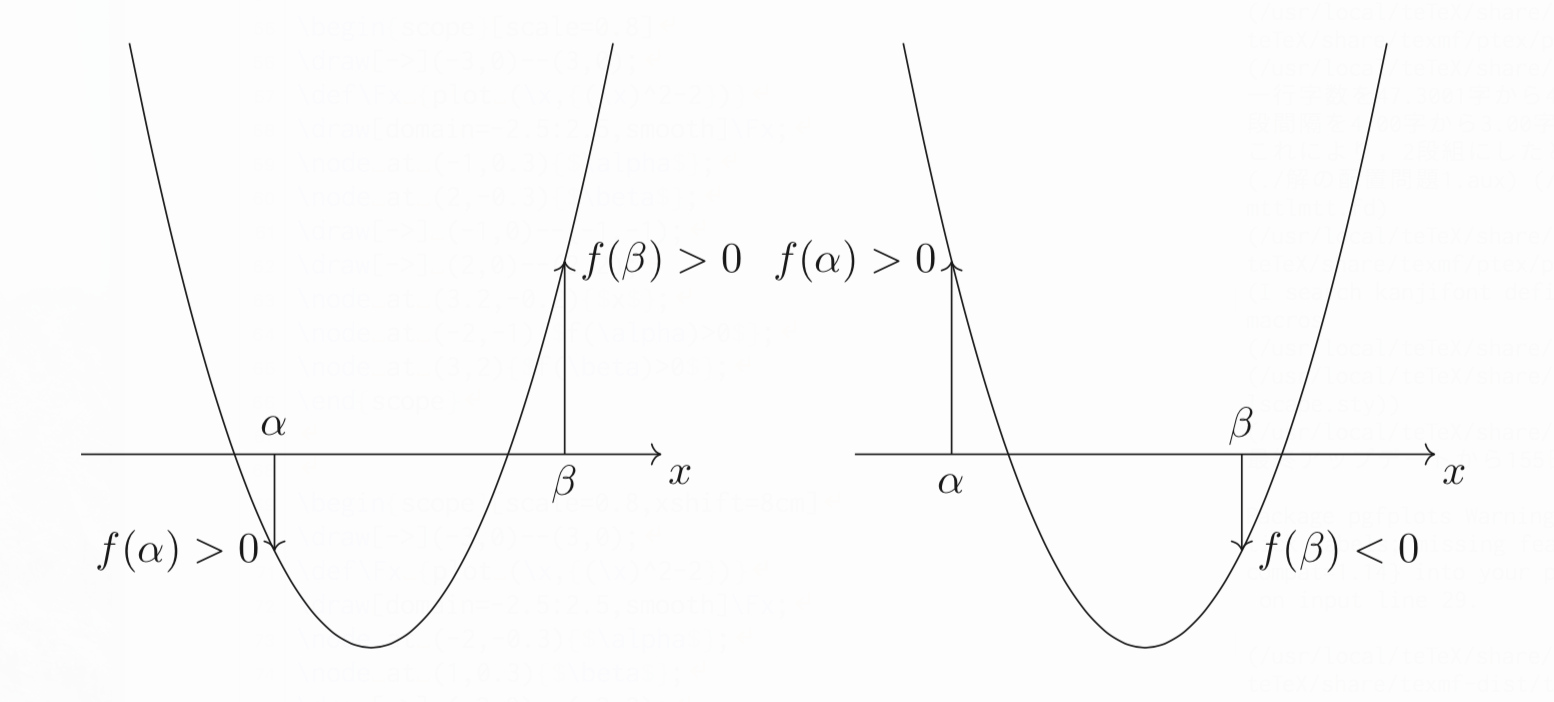
この状況になるのは、数式で表せば、

f(α)f(β)<0f(\alpha)f(\beta)<0

ですね。しかし、これ以外にもただ1つの実数解を持つ場合があります。

まず、与えられた範囲の端点を解に持って、かつ、与えられた範囲の中に解を持つ、以下の図のような場合が考えられます。

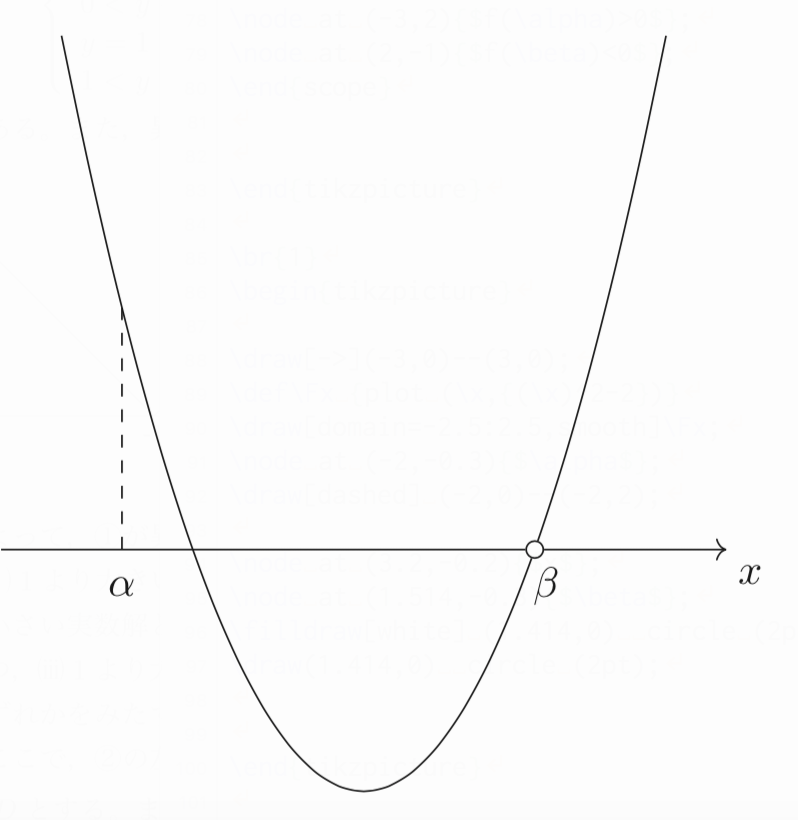
このように、与えられた範囲の端点が解になっているパターンというのは、場合分けの必要が生じることが多々あるので、いつも気をつけておきたいところです。

解の配置問題では、与えられた範囲の端点が解になるときを場合分けする必要があることが多い

さらに、重解を持つ場合も解がちょうど1つの場合に該当しますよね。重解を持って、かつ、その解が与えられた範囲に入っていればいいので、

{D=0α<軸<β\left\{\begin{array}{l}D=0\\\alpha<\text{軸}<\beta\end{array}\right.

という条件を考えればOKです。

問題3

xxの2次方程式

x2+ax+a2−3=0x^2+ax+a^2-3=0

が−1≦x≦32-1\leqq x\leqq \frac{3}{2}の範囲に少なくとも1つの実数解を持つような実数aaの条件を求めよ。

解答

x2+ax+a2−3=(x+a2)2+34a2−3x^2+ax+a^2-3=\left(x+\frac{a}{2}\right)^2+\frac{3}{4}a^2-3

であるから、与えられた式の左辺をf(x)f(x)とおくと、y=f(x)y=f(x)の軸はx=−fraca2x=-frac{a}{2}また、f(x)=0f(x)=0の判別式をDDとすると、求める条件は、

{D≧0−1≦−a2≦32f(−1)≧0f(32)≧0またはf(−1)f(32)≦0⇔{−3a2+12≧0−3≦a≦2a2−a−2≧0a2+32a−34≧0または(a2−a−2)(a2+32a−34)≦0⇔−2≦a≦−3−214または−3−214≦a≦−1または−3+214≦a≦2⇔−2≦a≦−1または−3+214≦a≦2\begin{align*}&\left\{\begin{array}{l}D\geqq 0\\-1\leqq -\frac{a}{2}\leqq \frac{3}{2}\\f(-1)\geqq 0\\f\left(\frac{3}{2}\right)\geqq0\end{array}\right.\text{または}f(-1)f\left(\frac{3}{2}\right)\leqq0\\\Leftrightarrow &\left\{\begin{array}{l}-3a^2+12\geqq 0\\-3\leqq a\leqq 2\\a^2-a-2\geqq 0\\a^2+\frac{3}{2}a-\frac{3}{4}\geqq0\end{array}\right.\text{または}(a^2-a-2)\left(a^2+\frac{3}{2}a-\frac{3}{4}\right)\leqq 0\\\Leftrightarrow &-2\leqq a\leqq\frac{-3-\sqrt{21}}{4}\text{または}\frac{-3-\sqrt{21}}{4}\leqq a\leqq -1\text{または}\frac{-3+\sqrt{21}}{4}\leqq a\leqq 2\\\Leftrightarrow &\boldsymbol{-2\leqq a\leqq -1\text{または}\frac{-3+\sqrt{21}}{4}\leqq a\leqq 2}\end{align*}

解説

少なくとも1つの解を持つパターンというのは、今までに扱った「ただ1つの実数解を持つ」というパターンと「相異なる2つの実数解を持つ」というパターンを合わせたものになります。

そのため、場合分けが多くなりそうに思われがちですが、実は、与えられた範囲の両端に等号がついていれば、細かく場合分けすることなく、上の解答のようにシンプルに記述することができます。

 

上の解答では、「与えられた範囲に重解もしくは相異なる2つの実数解を持つ場合」「端点の符号が異符号、もしくはどちらかが0になる場合」の2つで場合分けがなされています。

この場合分けのしかたが絶妙であり、これは、ダブリはあるものの漏れのない場合分けになっています。

 

たとえば、a=−3−214a=\frac{-3-\sqrt{21}}{4}のときは、下図のような状況になっており、これは上の2つの場合分けのどちらにも含まれます。

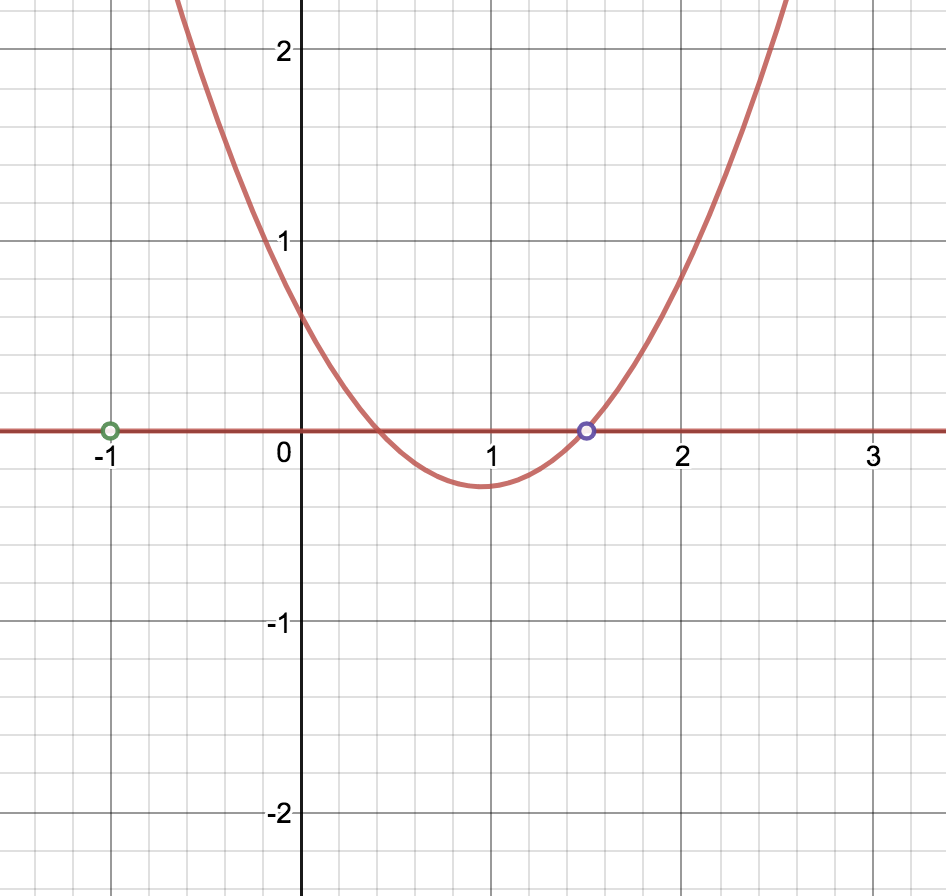
このように、相異なる2つの解を持つときと、ただ1つの実数解を持つときとで場合分けをせずに、ダブリはあっても漏れのない絶妙な場合分けをしてあげることがポイントとなります。

数式でまとめると、

α≦x≦β\alpha\leqq x\leqq \betaの範囲に、少なくとも1つの実数解を持つための条件は、

{D≧0α≦軸≦βf(α)≧0f(β)≧0またはf(α)f(β)≦0\left\{\begin{array}{l}D\geqq 0\\\alpha\leqq \text{軸}\leqq \beta\\f(\alpha)\geqq 0\\f(\beta)\geqq 0\end{array}\right.\text{または}f(\alpha)f(\beta)\leqq 0

問題4

xxの2次方程式

x3−3x−a=0x^3-3x-a=0

が0<x120<x\frac{1}{2}の範囲に実数解を持つような実数aaの条件を求めよ。

解答

x3−3x−a=0⇔x3−3x=ax^3-3x-a=0\Leftrightarrow x^3-3x=a

この方程式の解は、y=x3−3xy=x^3-3xとy=ay=aのグラフの共有点のxx座標に等しい。この左辺をf(x)f(x)とおくと、

f′(x)=3x2−3=3(x−1)(x+1)f^{\prime}(x)=3x^2-3=3(x-1)(x+1)

より、増減表は以下のようになる。

x⋯−1⋯1⋯f′(x)+0−0+f(t)↗2↘−2↗\begin{array}{|c||c|c|c|c|c|}\hline x &\cdots & -1 & \cdots & 1 & \cdots \\\hline f'(x) & + & 0 & - & 0 & + \\\hline f(t) &\nearrow & 2 & \searrow & -2 & \nearrow \\\hline\end{array}

よって、グラフは以下。

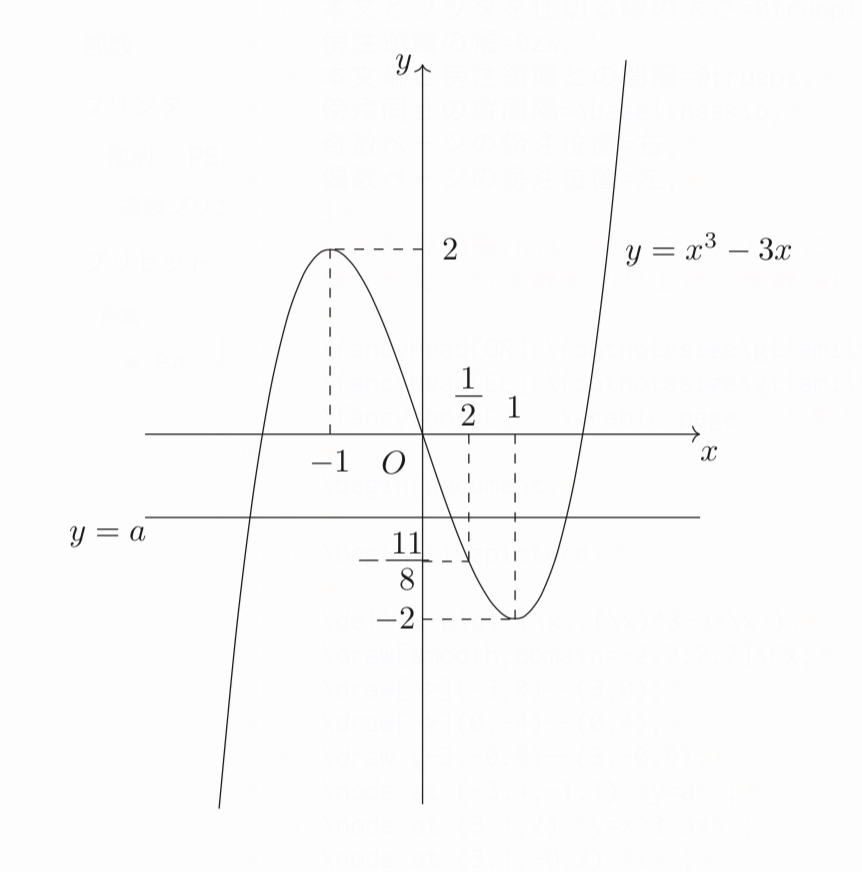
したがって、求める条件は、

−118<a<0\boldsymbol{-\frac{11}{8}<a<0}

解説

解の配置問題に限らず、高次方程式の解について考えるとき、定数部分にのみ文字定数が含まれていたら、その定数を分離します。

さらに、方程式の議論をグラフの共有点の議論に持っていけば、xx軸に平行な上下する直線と高次関数について視覚的に考えるだけになり、解についての議論が非常に楽になります。

 

上の答案で定数分離をしていない場合は3次関数が変化していく以下の動画のようになり、考えるのが難しくなってしまいますよね。

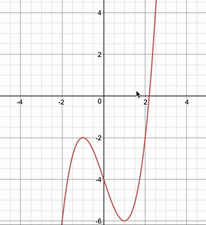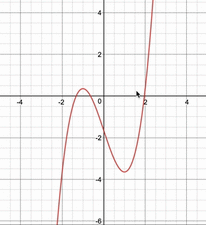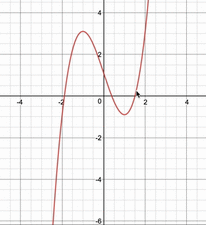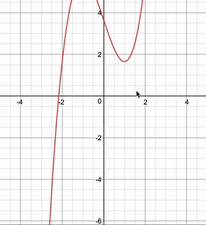
「高次方程式の解について考えるときは定数分離」というのを必ず覚えておきましょう。

まとめ

・解の配置問題は「相異なる2つ」「ただ1つ」「少なくとも1つ」「3次以上」の4パターン

・はじき(判別式、軸、境界(端点))を考えて解く！

・相異なる2つの場合は

{D>0α<軸<βf(α)>0f(β)>0\left\{\begin{array}{l}D>0\\\alpha<\text{軸}<\beta\\f(\alpha)>0\\f(\beta)>0\end{array}\right.

・ただ1つの場合は端点の場合分けに気をつける

・少なくとも1つの場合は、範囲の端に等号がついていれば、

{D≧0α≦軸≦βf(α)≧0f(β)≧0またはf(α)f(β)≦0\left\{\begin{array}{l}D\geqq 0\\\alpha\leqq \text{軸}\leqq \beta\\f(\alpha)\geqq 0\\f(\beta)\geqq 0\end{array}\right.\text{または}f(\alpha)f(\beta)\leqq 0

・3次以上の関数は定数分離

関連記事

「数ⅠAⅡB」の記事をもっと見る →

この記事を書いた人

管

齋藤 航貴

東京大学医学部医学科卒の医師。受験本番ではセンター数学満点、東大2次試験の数学は104点。東大受験を突破した経験を活かして、主に受験数学に関する記事を執筆しています。

プロフィール詳細 →

コメント

コメントを読み込み中...

コメントを投稿

数式は $...$、別行立ての数式は $$...$$ で入力できます。