この記事を読むとわかること
・共通テスト(旧センター試験)数学で満点を取るためのコツ
・計算をはやくするために使っていた裏技3つ
共通テストだけでなく、数学全般の勉強法を知りたいという方にはこちらの記事がおすすめです!↓
共通テストの数学で満点を取るためのコツは?
共通テストの数学ⅠAⅡBで満点を取るのって意外と難しいですよね…
そこで、共通テスト(当時の名称はセンター試験)本番で数学満点を達成した私が、満点を取るための勉強法やコツを伝授したいと思います!コツは3つあります。
1.10分以上余らせて解けるように練習する
2.ミスに気が付きやすい分野選択をする
3.計算がはやくなる裏技を駆使する
それぞれについて詳しく説明していきます!
10分以上余らせて解けるように練習する
共通テスト前には、過去問や共通テスト模試を解いて練習すると思いますが、そのときに時間ギリギリで解き終わるのではなく、少なくとも10分は余らせて解き終わることができるようになるまで練習しましょう。
共通テストの数学で満点を取っている人のほとんどは、10分以上余らせて解き終わり、残りの時間を見直しに充てています。まずは、満点を取るためにはやく解くという練習をするとよいでしょう。
私の場合は、10分以上余らせて解くのを完璧にするために、3段階で特訓していました。
1段階目は、共通テストの過去問をとりあえず満点を取れるかどうかは考えずにはやく解く練習です。そもそも、はやく解くという作業に慣れていなかったので、途中式をなるべく書かずに、短い時間で解き終えるということを練習しました。
これに、慣れてきたら2段階目では、余らせた時間を見直しに充てて、満点を狙うという練習をしました。ミスをしてしまったりもしましたが、解いている中で怪しいなと思った問題に戻る練習をしました。
3段階目では、共通テストの模試の問題で2段階目と同じことをやりました。一般に、共通テスト本番の数学よりも共通テスト模試の数学の方が計算量が多く、時間がきつくなることが多いです。そのため、同じ練習を共通テスト模試でやることによって、自然と計算がはやくなっていきます。
共通テスト模試ではやく解く練習をしていった結果、私は本番では数ⅠAで20分、数ⅡBで15分余らせて解き終えることができました!
私は東進の模試の過去問を使っていました。東進の問題は少し時間がキツく設定されていることが多いので、訓練には最適でした。
ミスに気づきやすい分野選択をする
過去問やセンター模試をたくさん解いていく中で、いつも数ⅠAの選択問題は適当に選んでいたんですが、ミスがよく起こるのは確率の分野を選択したときでした。
特に「本当は2で割らなければいけないのに割り忘れていた」といったようなミスが多く、解答欄にはピッタリ当てはまってしまうので、気づかぬまま解き進めてしまうことが多かったのです。
そこで、私は数ⅠAの整数、確率、図形の3つのうちいつも整数と図形を選択して、確率の問題は選択しないことに決めていました。図形の場合は、図に求めた値を書けば、値が大きくずれた時に違和感があるし、整数問題は検算が容易であることが多いなど、これらの分野はミスに気づきやすいのです。
このように、自分でミスに気づきやすい分野を選択して解くことによって、ミスの起こる頻度を最小限に抑えることができました。
計算がはやくなる裏技を使う
共通テストで時間を余らせて解くというスキルを身につけるには、単純に計算力が高くなることがもちろん最も大事です。
しかしながら、センター試験では、途中式を書かずに答えだけを書けばいいというだけあって、答えを簡単に求めるための裏技がいくつか存在します。
そこで、私が使っていた、計算をはやくするための裏技3つを教えたいと思います!
共通テストの数学で計算をはやくするための裏技
共通テストの数学で計算をはやくするための裏技3つ!
1.$\frac{1}{6}$公式、$\frac{1}{12}$公式
2.(等差)×(等比)型の数列の総和を和の中抜けで求める方法
3.サラスの公式
それぞれについて詳しく説明していきます!
1/6公式、1/12公式
$\frac{1}{6}$公式と$\frac{1}{12}$公式はかなり有名だと思いますが、放物線と直線によって囲まれた面積を求めるときの公式です。
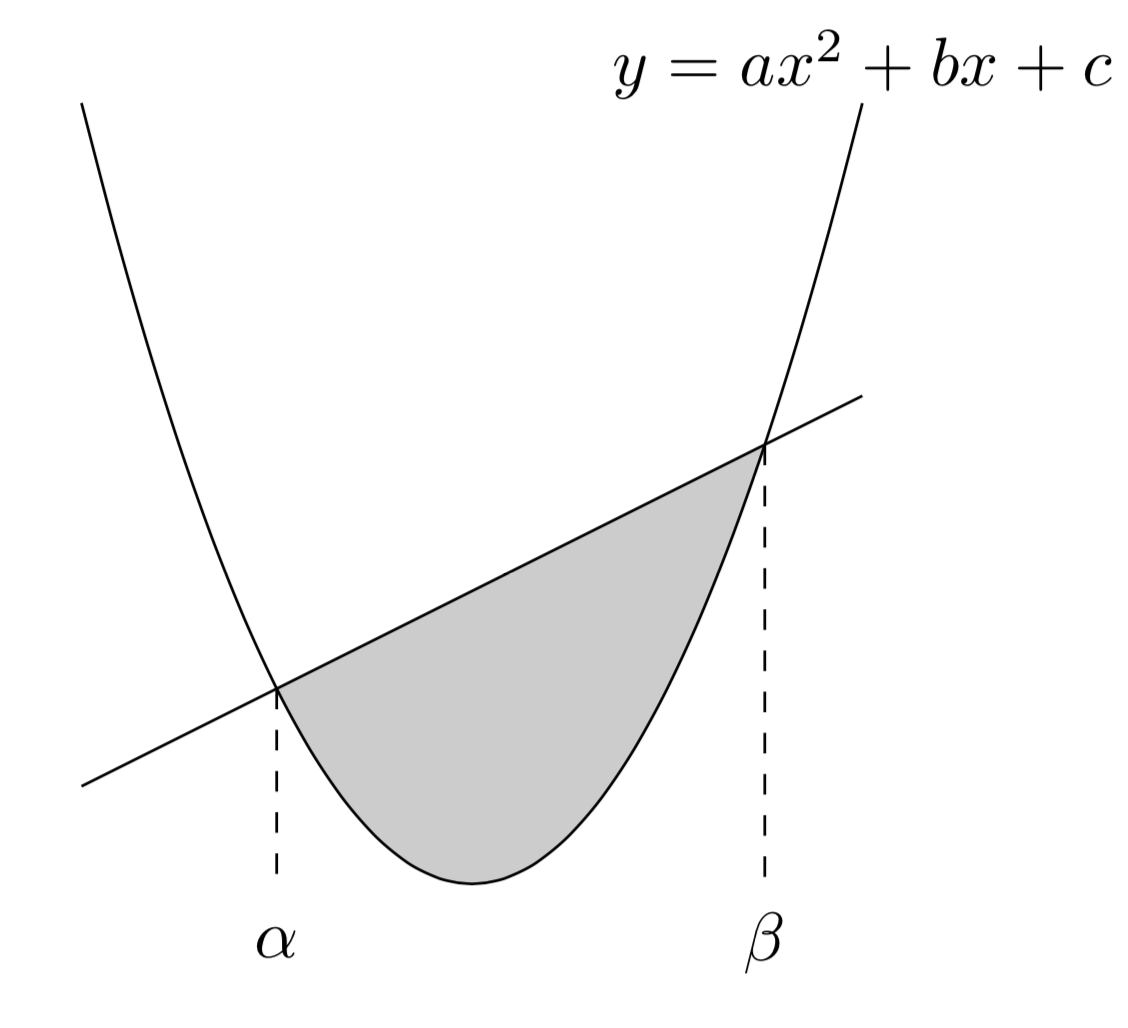
下図のように、2次の係数が$a$の2次関数と直線が2点で交わっており、その2点の$x$座標がそれぞれ$\alpha,\,\beta(\alpha<\beta)$であるとき、下図の斜線部の面積は、
\[\frac{|a|}{6}(\beta-\alpha)^3\]
になります。これが$\frac{1}{6}$公式です。
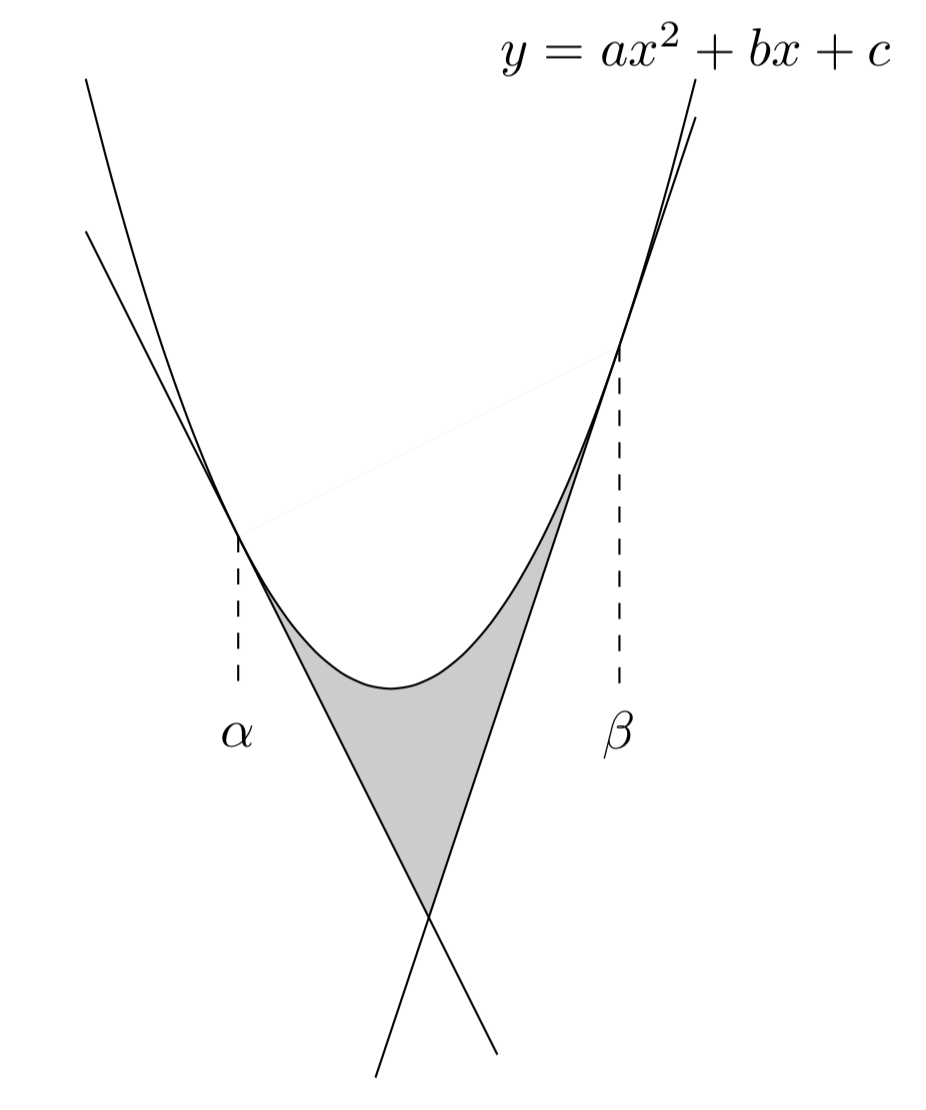
また、下図のように、2つの接線と放物線に囲まれた部分の面積は、
\[\frac{1}{12}(\beta-\alpha)^3\]
となります。これが$\frac{1}{12}$公式です。
これらを覚えておけば、放物線と直線で囲まれた面積を非常に素早く求めることができます!
ただし、2次の係数が$a$となっているときには、$|a|$をかけないといけないことに注意してくださいね。
(等差)×(等比)型の数列の総和を和の中抜けで求める方法
受験生が間違いやすく、また時間のかかる計算問題として有名なのが(等差)×(等比) 型の数列の総和を求める問題です。
一般の参考書では、公比をかけてから差をとるという手法によって求める求め方が教えられていますが、計算ミスが非常に多く、また時間もかかってしまいます。
そこで、和の中抜けという手法を用いることによって、総和計算を劇的にはやく、しかもミスなくできるようになります。私はこの手法を知ってからこの計算で一度もミスをしたことがありません。
詳しくはこちらの記事に書いてあるので読んでみてください。
サラスの公式
サラスの公式というのは、四面体の体積を求めるための公式です。
4点$\mathrm{O}(0,0,0)$、$\mathrm{A}(x_1,\,y_1,\,z_1)$、$\mathrm{B}(x_2,\,y_2,\,z_2)$、$\mathrm{C}(x_3,\,y_3,\,z_3)$が四面体を作っているとき、四面体$\mathrm{OABC}$の体積は、
\[\frac{1}{6}|x_1y_2z_3+x_2y_3z_1+x_3y_1z_2-x_1y_3z_2-x_2y_1z_3-x_3y_2z_1|\]
で求まります。これがサラスの公式です。
$x,\,y,\,z$の順に並べて、添字が$1\rightarrow 2\rightarrow 3$と変化しているときには符号はプラス、逆に変化しているときには符号はマイナスになると覚えやすいです!
共通テストの数ⅡBではベクトルの範囲で四面体を扱う問題が多いので、サラスの公式は非常に有効です。
まとめ
共通テストの数学で満点を取るコツは
1.10分以上余らせて解けるように訓練する
2.数ⅠAではミスに気づきやすい整数と図形を選択する
3.計算をはやくする裏技3つを覚えて使いこなす





