2019年のセンター試験(共通テスト)数学ⅠAでは、確率漸化式に似た内容の確率の問題が出たことで話題になりました。
その解答・解説を作成しました!
2019年センター試験(共通テスト)数学ⅠA第3問確率の解答
ア:4 イ:9 ウ:1 エ:6 オ:7 カキ:18 ク:1 ケ:6 コサ:43 シスセ:108 ソタチ:259 ツテト:648 ナニ:21 ヌネ:43 ノネ:88 ヒフへ:259
2019年センター試験(共通テスト)数学ⅠA第3問確率の問題・解説
(1)の問題・解説
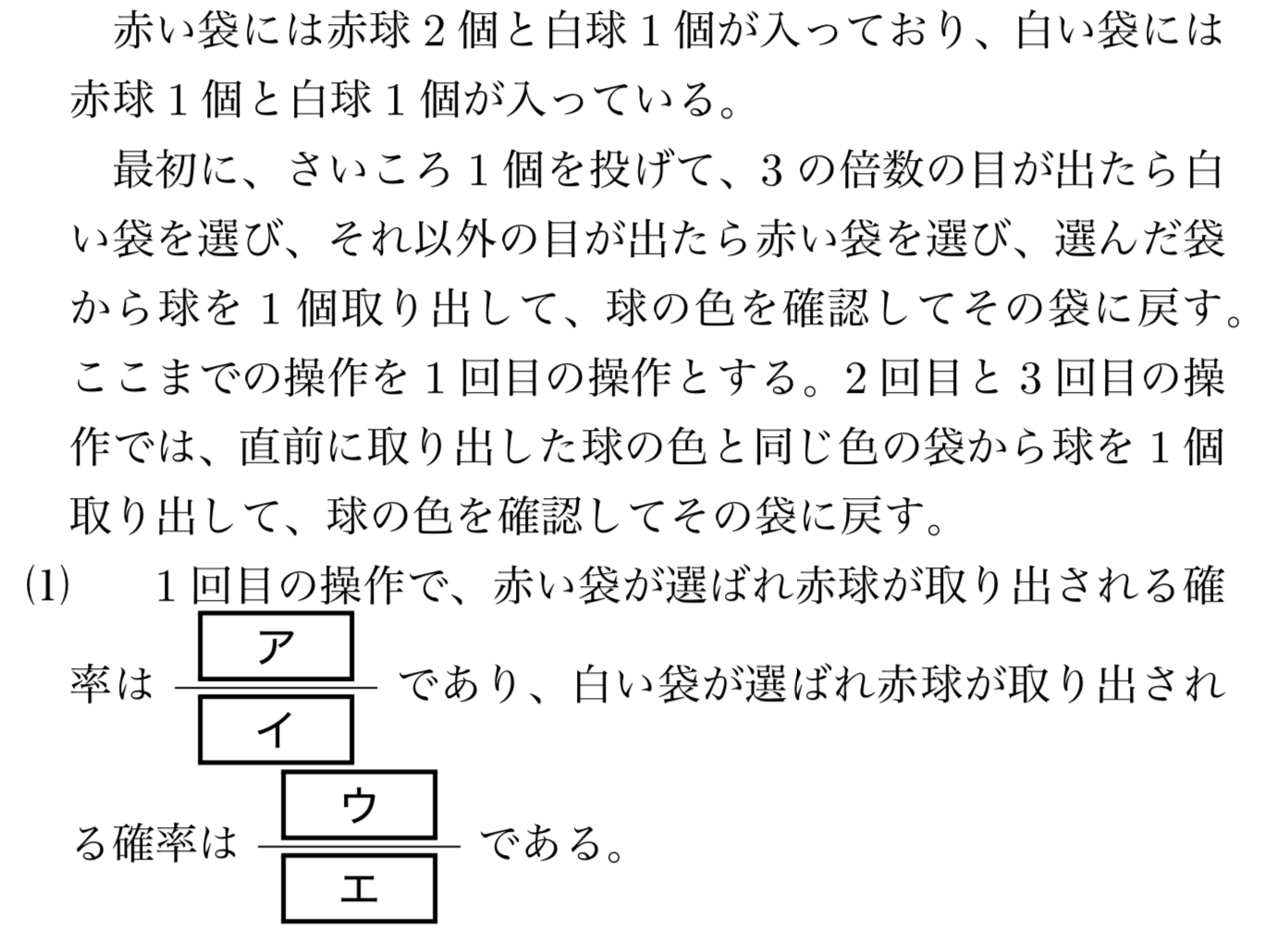
1回目の操作で赤い袋を選ぶ確率は$\frac{2}{3}$であり、赤い袋の中から赤球を選ぶ確率は$\frac{2}{3}$なので、
\[\frac{2}{3}\cdot\frac{2}{3}=\boldsymbol{\frac{4}{9}}\]
1回目の操作で白い袋を選ぶ確率は$\frac{1}{3}$であり、白い袋の中から赤球を選ぶ確率は$\frac{1}{2}$なので、
\[\frac{1}{3}\cdot\frac{1}{2}=\boldsymbol{\frac{1}{6}}\]
(2)の問題・解説

2回目の操作が白い袋で行われる確率は、1回目で白球を選ぶ確率に等しく、それは、1回目で赤球を選ぶ確率を$1$から引けば求まるので、(1)の結果より、
\[1-\left(\frac{4}{9}+\frac{1}{6}\right)=\boldsymbol{\frac{7}{18}}\]
(3)の問題・解説

2回目の操作で白球を選ぶパターンには、1回目で赤球を選んで、2回目に赤い袋から白球を取り出すパターンと、1回目で白球を選んで、2回目に白い袋から白球を取り出すパターンの2パターンしかない。
1回目で白球を選ぶ確率を$p$とすれば、1回目で赤球を選ぶ確率は$1-p$になる。それぞれのパターンにおいて、2回目で白球を選ぶ確率をかけて足すと、
\[\frac{1}{2}p+\frac{1}{3}(1-p)=\boldsymbol{\frac{1}{6}}p+\frac{1}{3}\]
ここで、1回目で白い球を取り出す確率は(2)より、$\frac{7}{18}$であるから、
\[\frac{1}{6}\cdot\frac{7}{18}+\frac{1}{3}=\boldsymbol{\frac{43}{108}}\]
先ほどの$\frac{1}{6}p+\frac{1}{3}$の関係は、2回目と3回目の間でも成り立つので、
\[\frac{1}{6}\cdot\frac{43}{108}+\frac{1}{3}=\boldsymbol{\frac{259}{648}}\]
このあたりの議論が確率漸化式に似ていますね!
(4)の問題・解説

条件付き確率についての問題です。条件付き確率についての復習をしておきましょう!
ある事象Aが起こったという条件のもとでの、事象Bが起こる確率のことを条件付き確率と呼び、その条件付き確率$P_A(B)$は、
\[P_A(B)=\frac{P(A\cap B)}{P(A)}\]
によって求められる。
2回目の操作で取り出した球が白球だったときに、その球を取り出した袋の色が白である(つまり1回目に白球を取り出している)確率は、上の定義式を見てあげれば、
\[\frac{(1回目も2回目も白球を取り出す確率)}{(2回目に白球を取り出す確率)}\]
で求まるので、
\[\frac{\frac{7}{18}\cdot\frac{1}{2}}{\frac{43}{108}}=\boldsymbol{\frac{21}{43}}\]
同様に、最後の問題は、
\[\frac{(1回目も2回目も赤球、3回目は白球を取り出す確率)}{(3回目に白球を取り出す確率)}\]
で求まるので、
\[\frac{\frac{11}{18}\cdot\frac{2}{3}\cdot\frac{1}{3}}{\frac{259}{648}}=\boldsymbol{\frac{88}{259}}\]



