2020年度のセンター試験(共通テスト)数学ⅠAの問題・解答・解説を見たい方はこちら
第1問(必答問題)
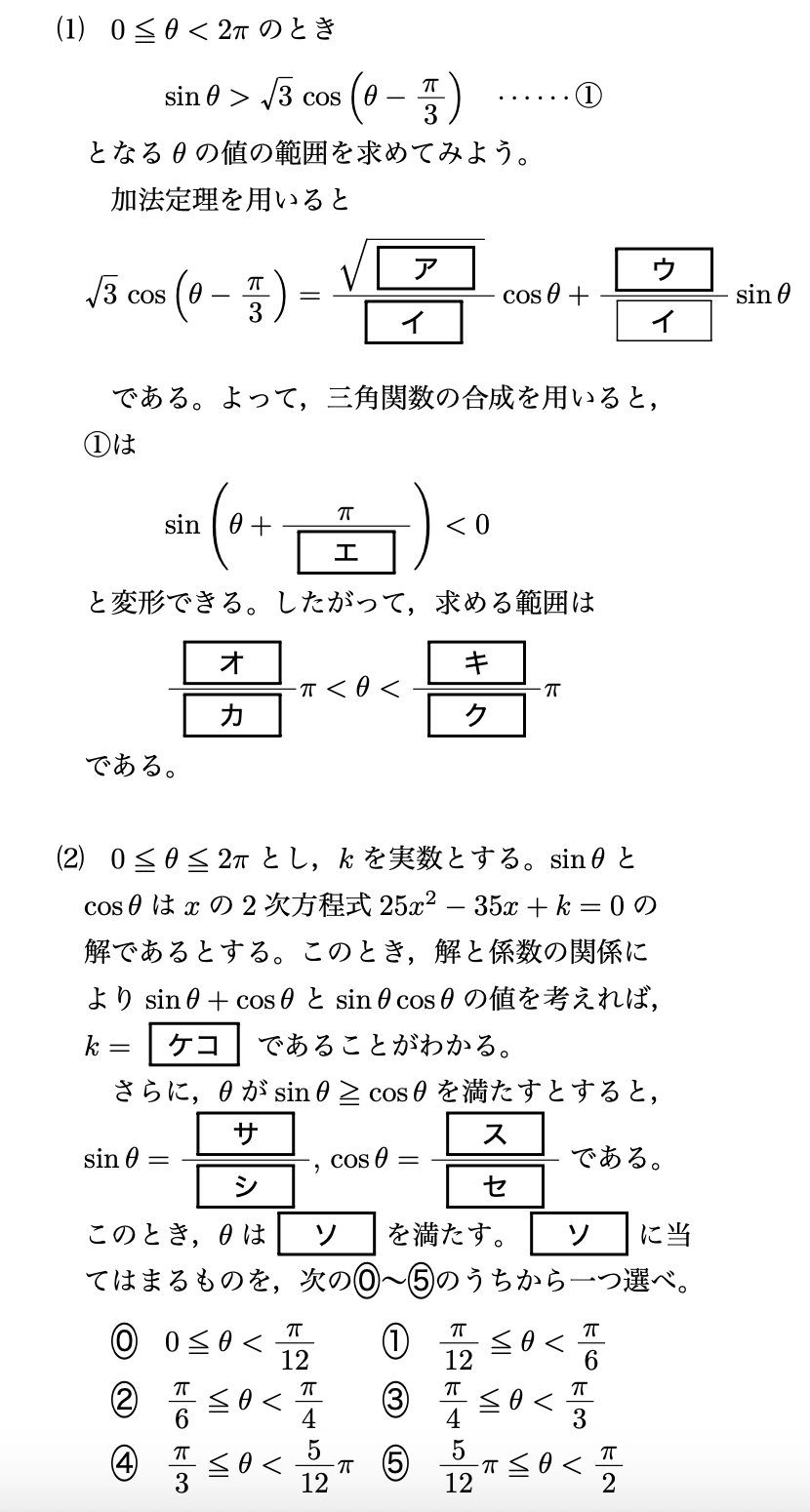
問題〔1〕
解答
ア:3 イ:2 ウ:3 エ:3 オ:3 カ:2 キ:5 ク:3 ケコ:12 サ:4 シ:5 ス:3 セ:5 ソ:3
解説
(1)$\cos$の加法定理は、
\[\cos(\alpha + \beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\]
であるので、
\[\begin{align*}&\sqrt{3}\cos\left(\theta-\frac{\pi}{3}\right)\\=&\sqrt{3}\cos\theta\cos\left(-\frac{\pi}{3}\right)-\sqrt{3}\sin\theta\sin\left(-\frac{\pi}{3}\right)\\=&\boldsymbol{\frac{\sqrt{3}}{2}}\cos\theta+\boldsymbol{\frac{3}{2}}\sin\theta\end{align*}\]
となります。これを用いて与えられた不等式を変形すると、
\[\frac{1}{2}\sin\theta+\frac{\sqrt{3}}{2}\cos\theta<0\]
となり、左辺について、三角関数の合成を適用すると、
\[\frac{1}{2}\sin\theta+\frac{\sqrt{3}}{2}\cos\theta=\sin(\theta+\alpha)\\(ただし\alphaは\sin\alpha=\frac{\sqrt{3}}{2},\,\cos\alpha=\frac{1}{2}を満たす実数)\]
と変形することができて、これを満たす$\alpha$のうち、解答欄に当てはまる形で書けるのは、
\[\alpha = \frac{\pi}{\boldsymbol{3}}\]
のときのみです。
$0\leqq \theta<2\pi$のとき、$\frac{\pi}{3}\leqq \theta+\frac{\pi}{3}<\frac{7}{3}\pi$であるから、
\[\sin\left(\theta+\frac{\pi}{3}\right)<0\Leftrightarrow \pi<\theta+\frac{\pi}{3}<2\pi \Leftrightarrow \boldsymbol{\frac{2}{3}}\pi<\theta<\boldsymbol{\frac{5}{3}}\pi\]
(2)解と係数の関係から、
\[\sin\theta + \cos\theta= \frac{35}{25}=\frac{7}{5}\]
が分かります。よって、
\[\begin{align*}&(\sin\theta + \cos\theta)^2=\left(\frac{7}{5}\right)^2\\\Leftrightarrow&1+2\sin\theta\cos\theta=\frac{49}{25}\\\Leftrightarrow&\sin\theta\cos\theta=\frac{12}{25}\end{align*}\]
解と係数の関係から、$\frac{k}{25}=\sin\theta\cos\theta$であるので、
\[k=\boldsymbol{12}\]
これで与えられた2次方程式の解が求められますね。
\[25x^2-35x+12=(5x-4)(5x-3)\]
と因数分解できるので、2解のうち大きい方が$\sin\theta$であるとき、
\[\sin\theta=\boldsymbol{\frac{4}{5}},\,\cos\theta=\boldsymbol{\frac{3}{5}}\]
となります。このときの$\theta$の値は、$\cos\theta=0.6<\frac{1}{\sqrt{2}}(=0.707\cdots)$であることを考えると、$\frac{\pi}{4}$よりは大きいですね。さらに、$\cos\theta=0.6>0.5$より、$\frac{\pi}{3}$よりは小さいこともわかります。したがって、
\[\boldsymbol{\frac{\pi}{4}\leqq\theta<\frac{\pi}{3}}\]
となります。
問題〔2〕

解答
タチ:11 ツテ:13 トナニ:-36 ヌ:2 ネノ:10 ハ:3 ヒフ:-4 へ:7 ホ:5
解説
(1)
$x=t^{\frac{1}{3}}$と置き換えてあげれば非常に見やすくなります。与えられた条件式は、
\[x-\frac{1}{x}=-3\]
であり、これの両辺を2乗すれば、
\[x^2+\frac{1}{x^2}-2=9\Leftrightarrow x^2+\frac{1}{x^2}=\boldsymbol{11}\]
と求まります。
さらに、
\[x^2+2+\frac{1}{x^2}=13\]
であるので、$x+\frac{1}{x}>0$であることに注意して、
\[x+\frac{1}{x}=\boldsymbol{\sqrt{13}}\]
また、
\[x^3-\frac{1}{x^3}=\left(x-\frac{1}{x}\right)\left(x^2+1+\frac{1}{x^2}\right)=-3\cdot 12=\boldsymbol{-36}\]
となります。
(2)
\[\log_3(x\sqrt{y})=\log_3x+\frac{1}{2}\log_3y\]
であるので、両辺を2倍して整理して、
\[\boldsymbol{2}X+Y\leqq \boldsymbol{10}\]
となります。
また、③の左辺は、
\[\log_{81}\frac{y}{x^3}=\log_{81}y-3\log_{81}x\]
と変形できて、さらに底の変換公式から、
\[\log_{81}y=\frac{\log_{3}y}{\log_{3}81}=\frac{Y}{4}\]
\[\log_{81}x=\frac{\log_{3}x}{\log_{3}81}=\frac{X}{4}\]
と変形できることも考えると、
\[\frac{Y}{4}-\frac{3X}{4}\leqq 1\Leftrightarrow \boldsymbol{3}X-Y\geq\boldsymbol{-4}\]
と変形できます。
これら2つを$XY$平面上に図示してあげると以下のようになります。
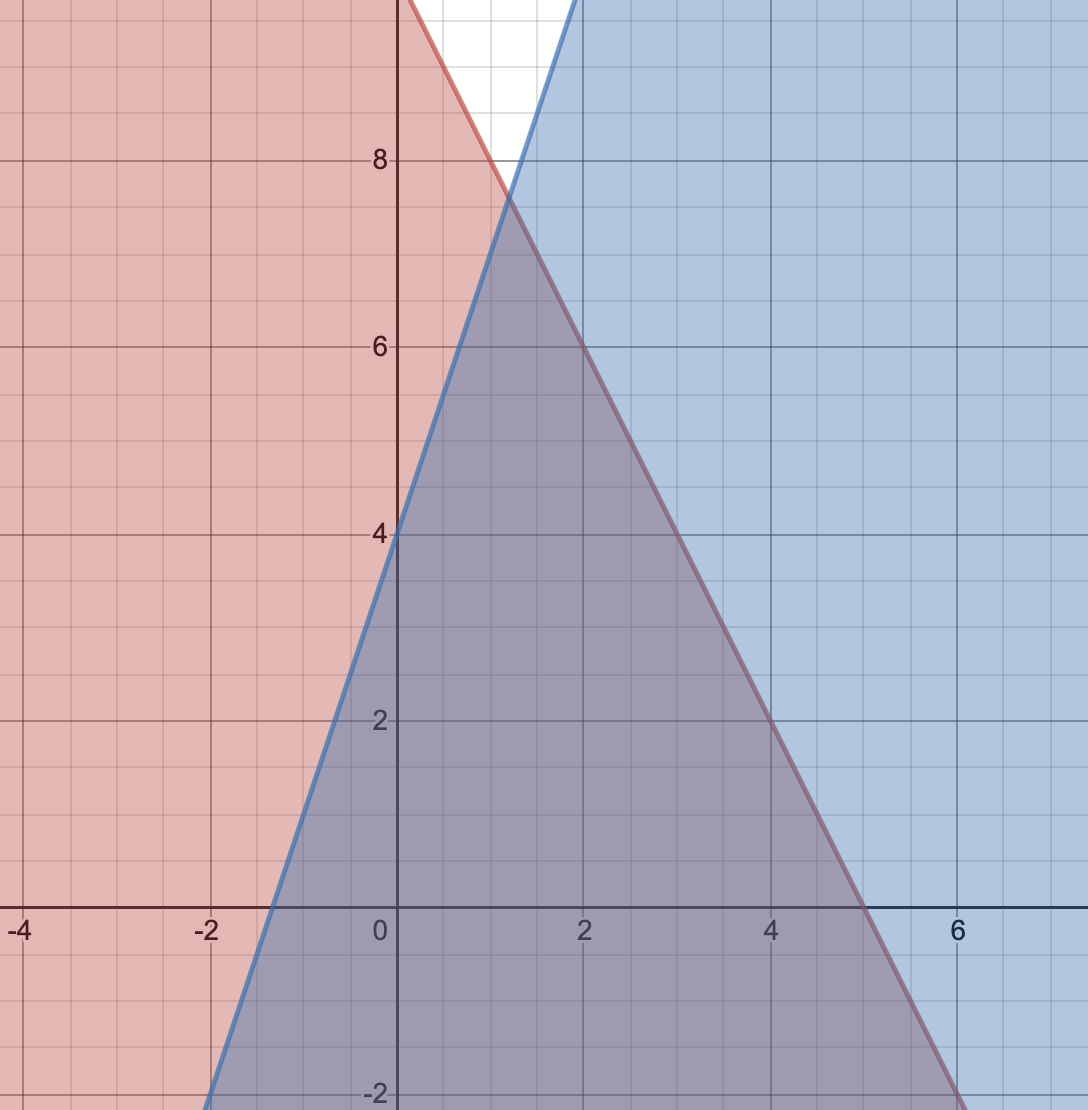
2式を同時にみたすときというのは、この青と赤の重なった領域内にあるときに等しく、このうち$y$が整数で最大になるのは、図から$Y=\boldsymbol{7}$のときだと分かります。
さらに$Y=7$であるとき、
\[1\leqq X\leqq \frac{3}{2}\Leftrightarrow 3\leqq x\leqq 3\sqrt{3}\]
であるので、$x$が整数で最大になるのは、$x=\boldsymbol{5}$のときです。
第2問(必答問題)
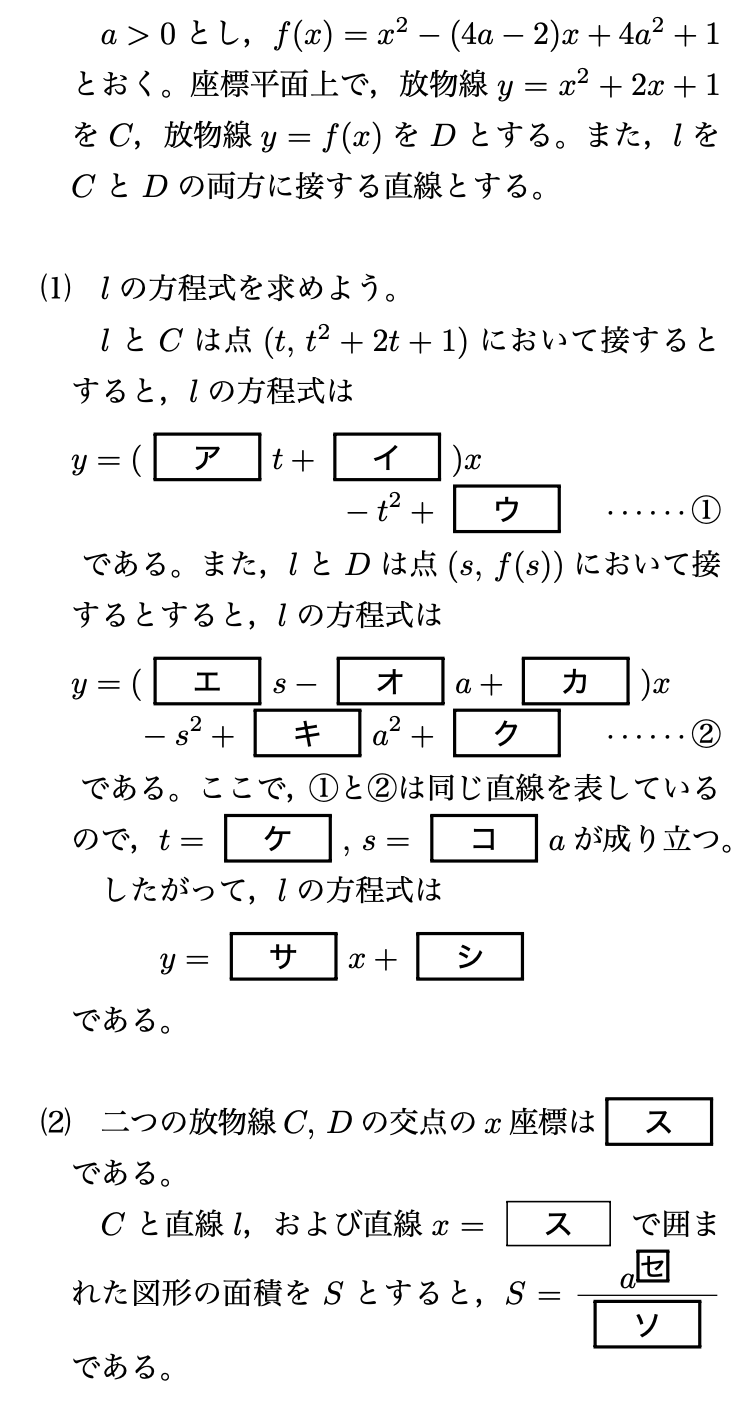
問題
解答
ア:2 イ:2 ウ:1 エ:2 オ:4 カ:2 キ:4 ク:1 ケ:0 コ:2 サ:2 シ:1 ス:a セ:3 ソ:3 タ:1 チ:1 ツ:3 テ:2 ト:4 ナ:2 ニ:1 ヌ:3 ネ:2 ノ:3 ハ:2 ヒフ:27
解説
(1)
$g(x)=x^2+2x+1$とおくと、
\[g'(x)=2x+2\]
となるので、$x=t$における$y=g(x)$に対する接線の方程式は、
\[y-g(t)=(2t+2)(x-t)\Leftrightarrow y=(\boldsymbol{2}t+\boldsymbol{2})x-t^2+\boldsymbol{1}\]
となります。
また、
\[f'(x)=2x-(4a-2)\]
であるので、$x=s$における$y=f(x)$に対する接線の方程式は、
\[\begin{align*}&y-f(s)=(2s-4a+2)(x-s)\\\Leftrightarrow &y=(\boldsymbol{2}s-\boldsymbol{4}a+\boldsymbol{2})x-s^2+\boldsymbol{4}a^2+1\end{align*}\]
となります。
これらはどちらも$l$を表しているので、同じ直線の方程式になっています。よって、係数を比較して、
\[\left\{\begin{array}{l}2t+2=2s-4a+2\\-t^2+1=-s^2+4a^2+1\end{array}\right.\]
が成り立ちますね。これを解くと、$t=\boldsymbol{0},\,s=\boldsymbol{2}a$が求まります。
$t=0$を先程の直線の式に代入すれば、
\[y=\boldsymbol{2}x+\boldsymbol{1}\]
と$l$の方程式が分かります。
(2)
$y=f(x)$と$y=g(x)$から$y$を消去して、
\[\begin{align*}&x^2-(4a-2)x+4a^2+1=x^2+2x+1\\\Leftrightarrow &4ax=4a^2\\\Leftrightarrow &x=\boldsymbol{a}(\because a)\end{align*}\]
と交点の$x$座標が求まります。
$C$と直線$l$と$x=a$で囲まれた図形は下図のようになります。
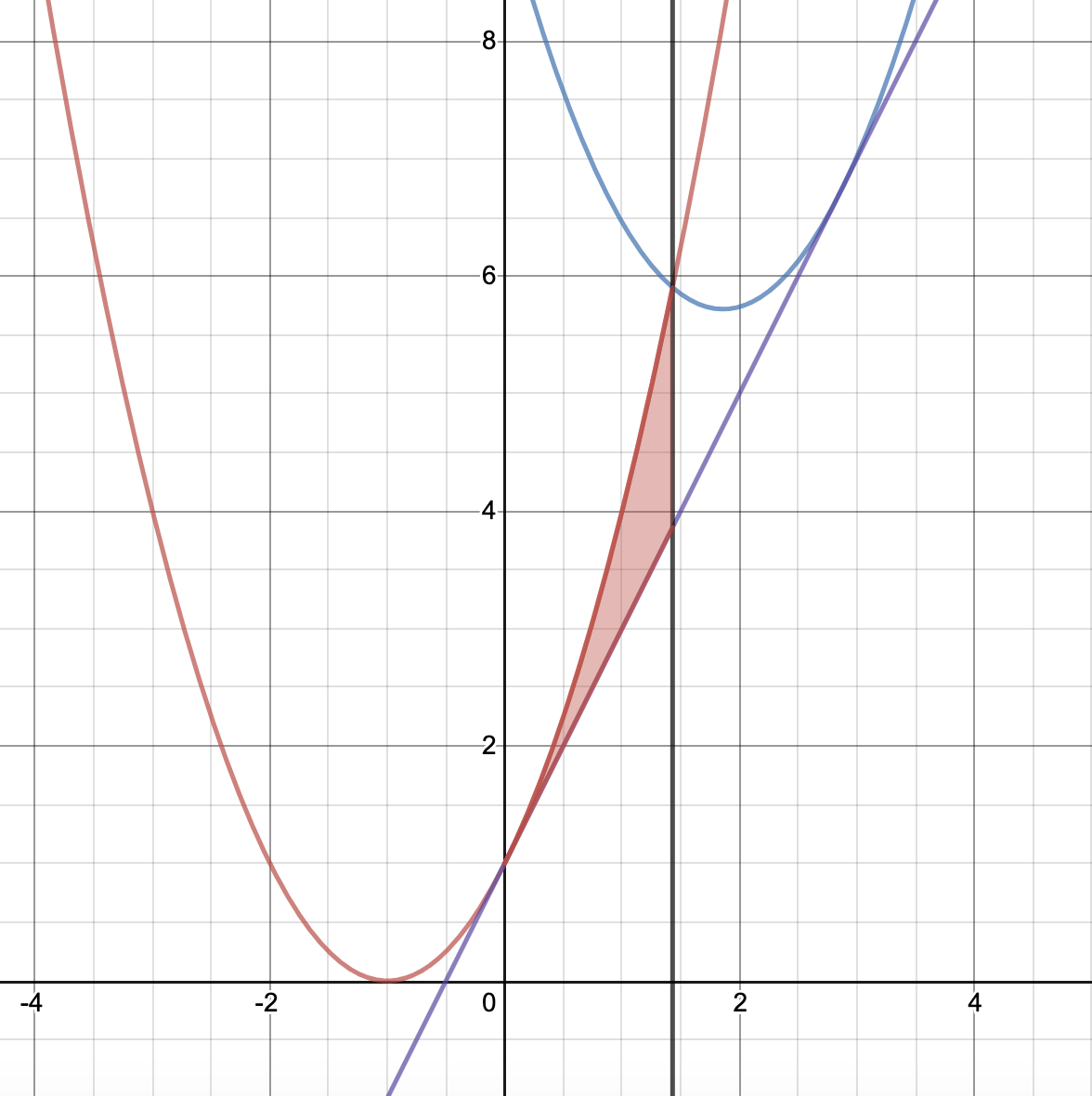
この面積は、
\[\int_{0}^{a}\{x^2+2x+1-(2x+1)\}dx=\left[\frac{x^3}{3}\right]_{0}^{a}=\frac{a^{\boldsymbol{3}}}{\boldsymbol{3}}\]
となります。
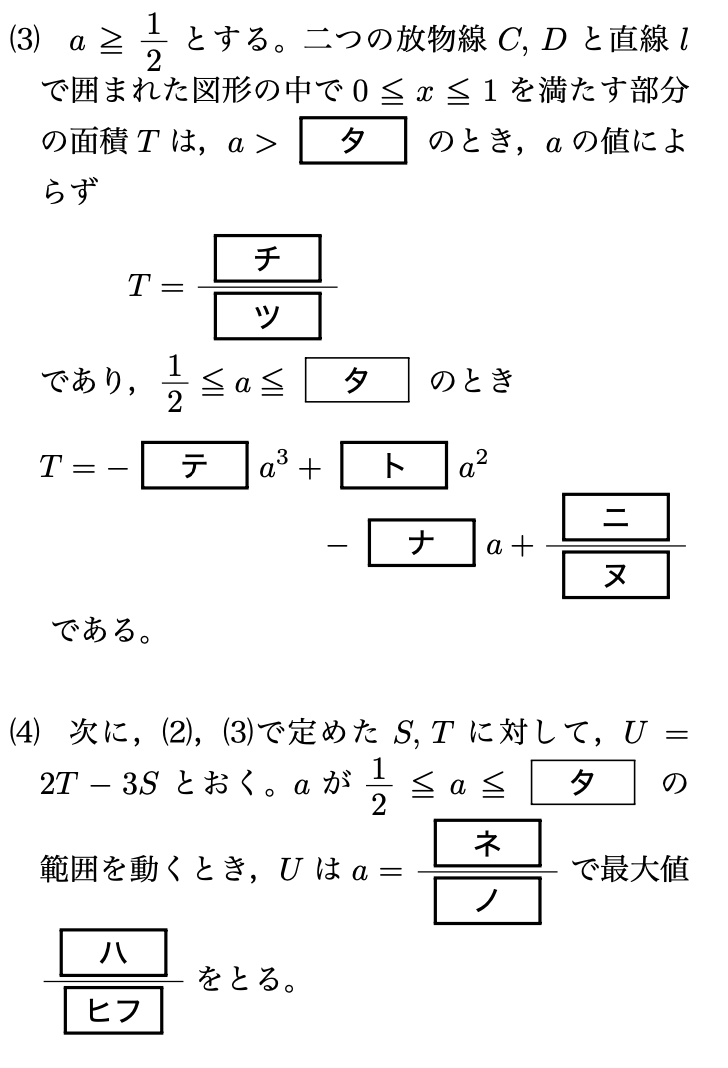
(3)
$C$と$D$と$l$で囲まれた部分のうち、$0\leqq x\leqq 1$を満たす部分は下の動画のようになります。($a=0.5$から少しずつ$a$の値を大きくしていく様子です。)

$a=1$のときを境目にして、図形の形が全く変わらなくなっているのが見て分かると思います。交点が$0\leqq x\leq1$の範囲に入っているかどうかで場合分けするだけですね。
$a\geqq \frac{1}{2}$という条件は、$D$と$l$の接点が$0\leqq x\leq1$の範囲に入らないようにするために付いているのも分かるでしょう。
よって、$a>\boldsymbol{1}$のときに$t$は一定で、先程求めた面積の式に$a=1$を代入して、
\[T=\boldsymbol{\frac{1}{3}}\]
また、$\frac{1}{2}\leqq a\leqq 1$のときは、
\[\begin{align*}&S+\int_{a}^{1}\{x^2-(4a-2)x+4a^2+1-(2x+1)\}dx\\=&\frac{a^3}{3}+\left[\frac{x^3}{3}-2ax^2+4a^2x\right]_{a}^{1}\\=&-\boldsymbol{2}a^3+\boldsymbol{4}a^2-\boldsymbol{2}a+\frac{\boldsymbol{1}}{\boldsymbol{3}}\end{align*}\]
(4)
$\frac{1}{2}\leqq a\leqq 1$のとき、
\[2T-3S=-5a^3+8a^2-4a+\frac{2}{3}\]
であり、この右辺を$h(a)$とすると、
\[h'(a)=-15a^2+16a-4=-(3a-2)(5a-2)\]
となるので、増減表は以下のようになります。
\[\begin{array}{|c||c|c|c|c|c|} \hline a&\frac{1}{2}&\cdots&\frac{2}{3}&\cdots&1\\\hline h'(a)&&+&0&-&\\\hline
h(a)&&\nearrow&\frac{2}{27}&\searrow&\\\hline\end{array}\]
したがって、$a=\boldsymbol{\frac{2}{3}}$のとき、最大値$\boldsymbol{\frac{2}{27}}$を取ることが分かりました。
第3問(選択問題)
問題
解答
ア:6 イ:0 ウ:1 エ:1 オ:2 カ:3 キ:1 ク:2 ケ:1 コ:1 サ:1 シ:6 ス:1 セ:2 ソ:2 タ:3 チ:1 ツ:3 テ:1 ト:4 ナ:1 ニ:2 ヌ:2 ネ:1 ノ:0 ハ:0 ヒ:1
解説
(1)
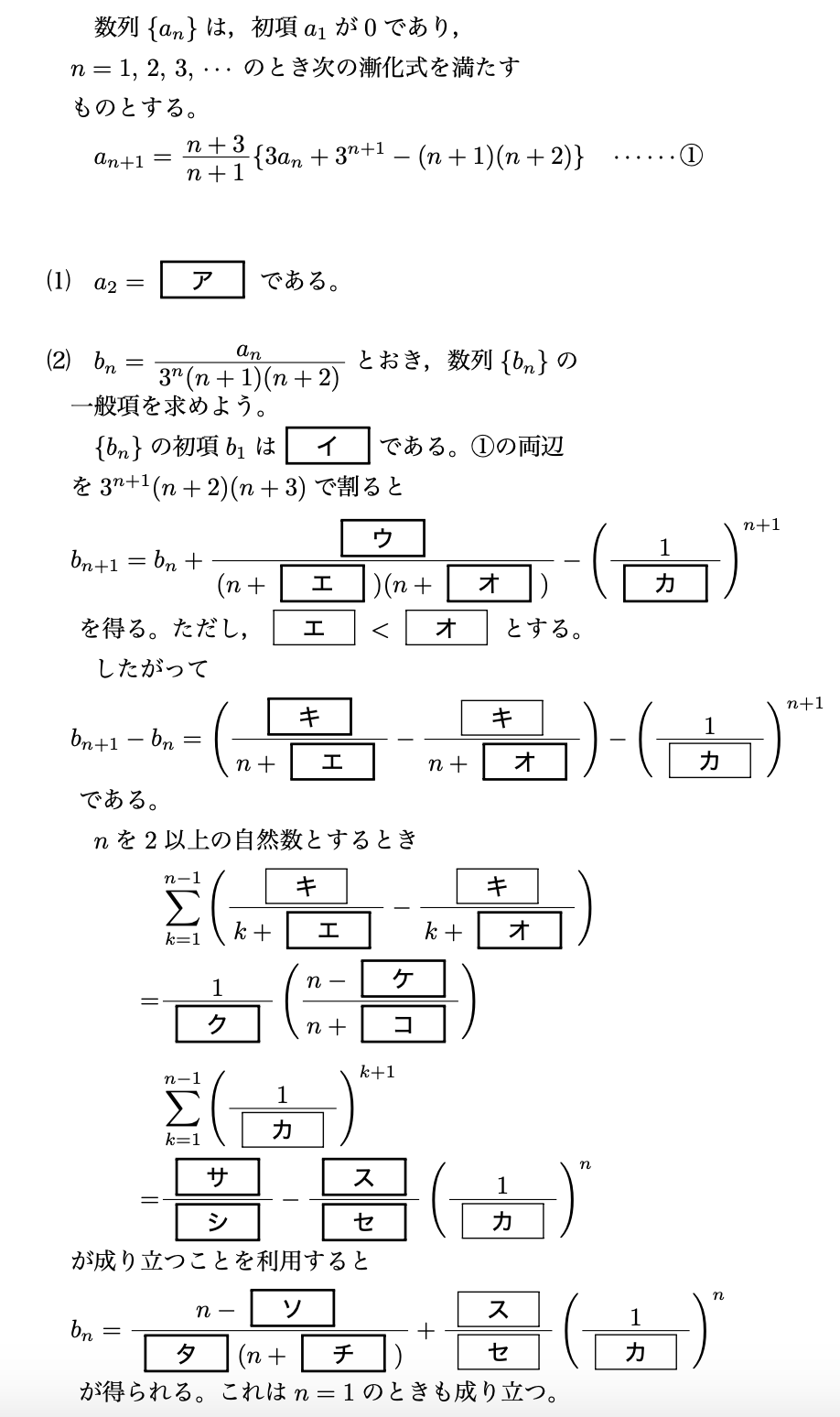
与えられた漸化式に$n=1$を代入して計算すると、
\[a_2=\frac{4}{2}(0+3^2-2\cdot 3)=\boldsymbol{6}\]
となります。
(2)
$n=1$を代入すると、$a_1=0$より、
\[b_1=\boldsymbol{0}\]
与えられた漸化式の両辺を$3^{n+1}(n+2)(n+3)$で割ると、
\[b_{n+1}=b_n+\frac{\boldsymbol{1}}{(n+\boldsymbol{1})(n+\boldsymbol{2})}+\left(\frac{1}{\boldsymbol{3}}\right)^{n+1}\]
となります。
よって、隣り合う項の差が分かっている状態になったので、階差数列の公式を使ってあげれば$b_n$の一般項を求められることに気づきます。
さて、階差数列の公式を使うとなると、
\[\sum\frac{\boldsymbol{1}}{(n+\boldsymbol{1})(n+\boldsymbol{2})}+\left(\frac{1}{\boldsymbol{3}}\right)^{n+1}\]
を計算しなければならないですね。後半部分はただの等比数列の総和の公式を使えばいいので、問題ないでしょう。前半部分については、分数の形の総和なので、「和の中抜け」を使うことになります。
和の中抜けについては以下の記事が詳しいです。
この部分の論理をすっ飛ばして突然式変形を要求されるような問題の構成になっていたので、戸惑った受験生も多かったかと思います。
変形すると、
\[b_{n+1}-b_n=\frac{\boldsymbol{1}}{n+1}-\frac{1}{n+2}+\left(\frac{1}{3}\right)^{n+1}\]
となります。
階差数列の公式は、$\sum_{k=1}^{n-1}$という形が出てくるので、$n\geqq 2$のときでしか使えないのでした。そのため、問題文では、「$n$を2以上の自然数とするとき」と書かれています。
和の中抜けを適用すると、
\[\sum_{k=1}^{n-1}\frac{1}{k+1}-\frac{1}{k+2}=\frac{1}{2}-\frac{1}{n+1}=\frac{1}{\boldsymbol{2}}\left(\frac{n-\boldsymbol{1}}{n+\boldsymbol{1}}\right)\]
と計算できます。
また、等比数列の和の公式から、
\[\sum_{k=1}^{n-1}\left(\frac{1}{3}\right)^{k+1}=\frac{\frac{1}{9}\left(1-\left(\frac{1}{3}\right)^{n-1}\right)}{1-\frac{1}{3}}=\frac{\boldsymbol{1}}{\boldsymbol{6}}-\frac{\boldsymbol{1}}{\boldsymbol{2}}\left(\frac{1}{3}\right)^n\]
となるので、これらと$b_1=0$から、階差数列の公式より
\[\begin{align*}b_n=&b_1+\frac{1}{2}\left(\frac{n-1}{n+1}\right)-\frac{1}{6}+\frac{1}{2}\left(\frac{1}{3}\right)^n\\=&\frac{n-\boldsymbol{2}}{\boldsymbol{3}(n+\boldsymbol{1})}+\frac{1}{2}\left(\frac{1}{3}\right)^n\end{align*}\]
これは$n=1$を代入すると$0$となるので、$b_n$の一般項はこれでよいことになります。
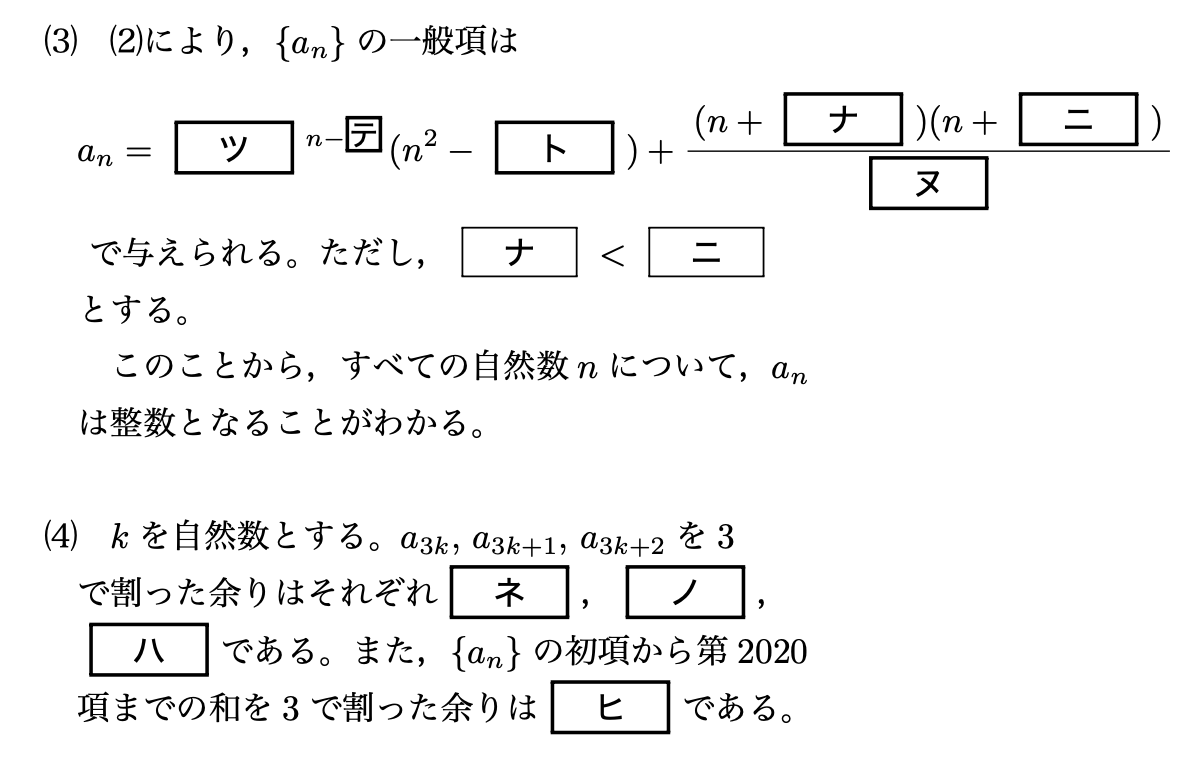
(3)
$b_n$の一般項が分かると、
\[b_n=\frac{a_n}{3^n(n+1)(n+2)}\]
と定義されていたことから、
\[\begin{align*}a_n=&3^n(n+1)(n+2)b_n\\=&\boldsymbol{3}^{n-\boldsymbol{1}}(n^2-\boldsymbol{4})+\frac{(n+\boldsymbol{1})(n+\boldsymbol{2})}{\boldsymbol{2}}\end{align*}\]
と$a_n$の一般項が求まりました!最初はすごく複雑な漸化式で面食らったかと思いますが、流れに乗って計算していくとちゃんと一般項が求まって嬉しいですね。
さて、この前半部分は整数で、後半部分についても、$(n+1)(n+2)$は連続2整数の積なので常に偶数であることを考えると、$\frac{(n+1)(n+2)}{2}$は常に整数となることがわかりますね。
そこで、これを3で割ったあまりについての問題が(4)に続いていきます。
(4)
$a_n$を3で割ったあまりについて考えるとき、
\[3^{n-1}(n^2-4)\]
の部分は3の倍数になることは即座に分かることが分かると思います。注意しなければならないのは、$n=1$のときは$3^{0}=1$となるので、「3のべき乗があるから3の倍数だ!」という論理が通用しないことです。幸い、$1^2-4=-3$より$(n^2-4)$の部分が3の倍数になっているので、そこまで考えられてなくても問題はありません。
よって、$a_n$を3で割った時のあまりは$\frac{(n+1)(n+2)}{2}$を3で割った時のあまりに等しいことが分かります。
以下合同式の法を3とすると、
$n\equiv 0$のとき
\[\frac{(n+1)(n+2)}{2}\equiv \frac{2}{2}=\boldsymbol{1}\]
$n\equiv 1$のとき
\[\frac{(n+1)(n+2)}{2}\equiv \frac{2\cdot 3}{2}=3\equiv \boldsymbol{0}\]
$n\equiv 2$のとき
\[\frac{(n+1)(n+2)}{2}\equiv \frac{3\cdot 4}{2}=6\equiv \boldsymbol{0}\]
となります。
よって、初項から第2020項までの和を3で割ったあまりについて考える時は、$n$が3の倍数のものが何回出てくるか考えればOKですね。
\[2020\div 3 = 673 \cdots 1\]
より、673を3で割ったあまりが答えになるので、
\[673\div 3 =224\cdots \boldsymbol{1}\]
第4問(選択問題)
問題
解答
ア:3 イ:6 ウ:4 エ:3 オカ:36 キク:-2 ケ:3 コ:1 サ:2 シ:6 ス:2 セ:2 ソタ:-4 チ:3 ツテ:30 ト:1 ナ:2 ニ:2 ヌ:1 ネ:2 ノ:2 ハヒ:60 フ:3 へ:4 ホ:3
解説
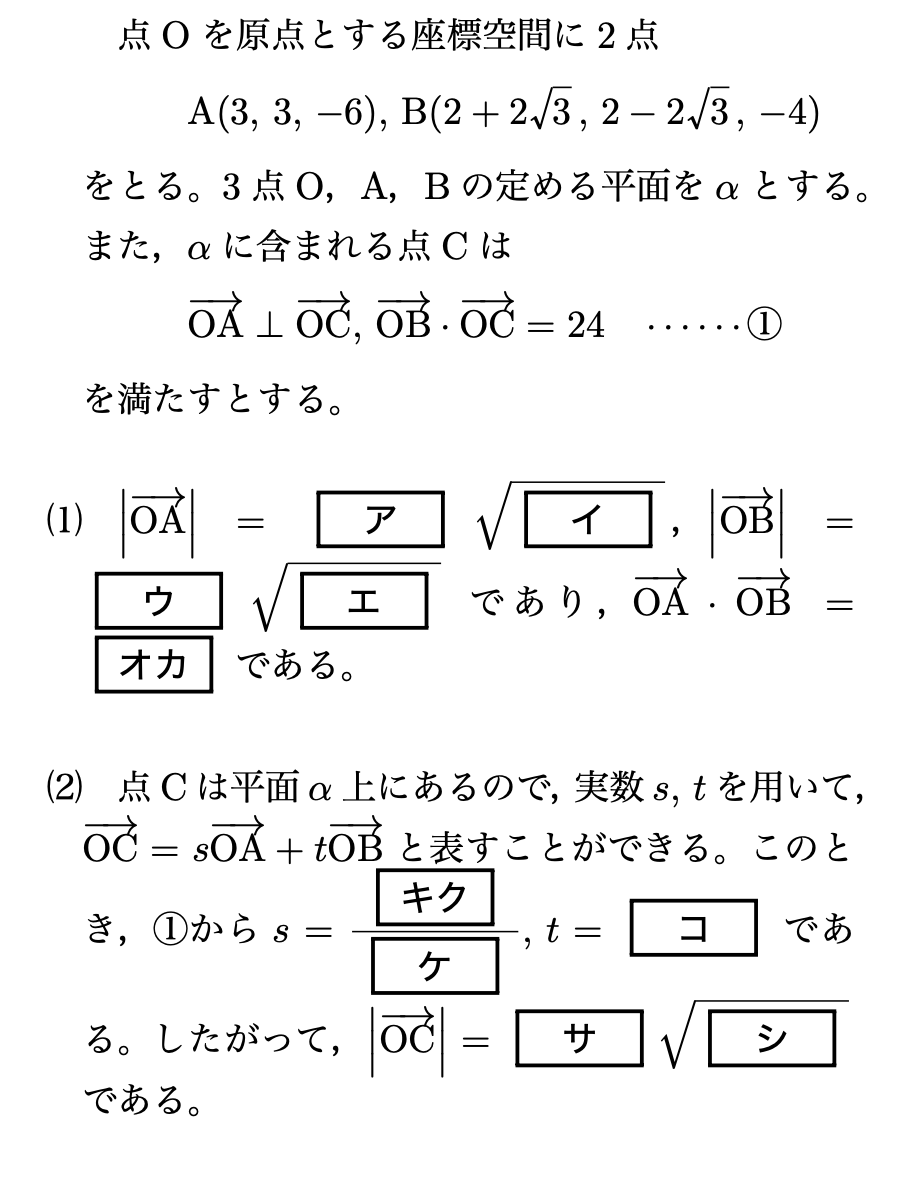
(1)
$\overrightarrow{\mathrm{OA}}=\vec{a}$、$\overrightarrow{\mathrm{OB}}=\vec{b}$と書くことにします。
\[\left|\vec{a}\right|=\sqrt{3^2+3^2+(-6)^2}=\boldsymbol{3}\sqrt{\boldsymbol{6}}\]
\[\left|\vec{b}\right|=\sqrt{(2+2\sqrt{3})^2+(2-2\sqrt{3})^2+(-4)^2}=\boldsymbol{4}\sqrt{\boldsymbol{3}}\]
\[\vec{a}\cdot\vec{b}=3(2+2\sqrt{3})+3(2-2\sqrt{3})+(-6)\cdot(-4)=\boldsymbol{36}\]
(2)
$\overrightarrow{\mathrm{OC}}=\vec{c}$と書くことにします。
\[\vec{c}=s\vec{a}+t\vec{b}\]
と書けるので、$\vec{a}\perp\vec{c}$、$\vec{b}\cdot\vec{c}=24$から、
\[\begin{align*}&\vec{a}\cdot (s\vec{a}+t\vec{b})=0\\\Leftrightarrow &s|\vec{a}|^2+t\vec{a}\cdot\vec{b}=0\\\Leftrightarrow & 54s+36t=0\\\Leftrightarrow & 3s+2t=0\end{align*}\]
\[\begin{align*}&\vec{b}\cdot (s\vec{a}+t\vec{b})=24\\\Leftrightarrow &s(\vec{a}\cdot\vec{b})+t|\vec{b}|^2=24\\\Leftrightarrow & 36s+48t=24\\\Leftrightarrow & 3s+4t=2\end{align*}\]
この2式を解いて、
\[s=\frac{\boldsymbol{-2}}{\boldsymbol{3}},\,t=\boldsymbol{1}\]
となるので、
\[\begin{align*}&|\vec{c}|^2\\=&\left|\frac{-2}{3}\vec{a}+\vec{b}\right|^2\\=&\frac{4}{9}\cdot |\vec{a}|^2-\frac{4}{3}\vec{a}\cdot\vec{b}+|\vec{b}|^2\\=&24\end{align*}\]
となります。したがって、
\[|\vec{c}|=\boldsymbol{2}\sqrt{\boldsymbol{6}}\]
(3)
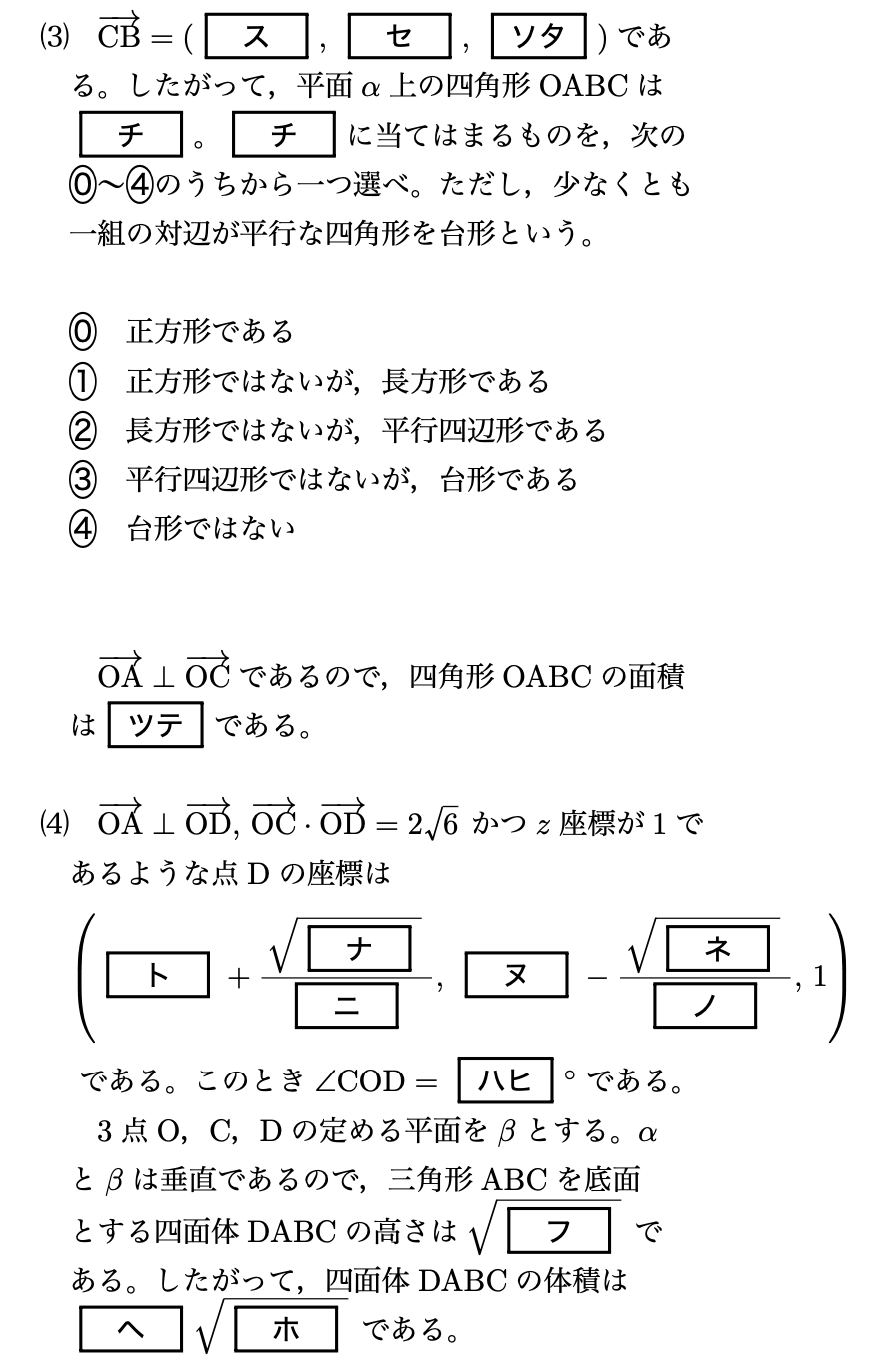
\[\overrightarrow{\mathrm{CB}}=\vec{b}-\vec{c}=\frac{2}{3}\vec{a}=(\boldsymbol{2},\,\boldsymbol{2},\,\boldsymbol{-4})\]
であるので、辺OAと辺CBは平行で、かつ辺の長さの比が2:3となっていることがわかります。よって、平行四辺形ではないが、台形であると言えます。
さらに、$\vec{a}\perp \vec{c}$より、$|\vec{c}|$が台形の高さにあたることが分かるので、面積は、
\[\frac{1}{2}\left(|\vec{a}|+\frac{2}{3}|\vec{a}|\right)\cdot|\vec{c}|=\boldsymbol{30}\]
となります。
(4)
点Dの座標を$(p,\,q,\,1)$とおいて、$\overrightarrow{\mathrm{OD}}=\vec{d}$と書くことにします。
\[\vec{a}\cdot\vec{d}=0\Leftrightarrow 3p+3q-6=0\Leftrightarrow p+q=2\]
また、$\vec{a}\cdot\vec{d}=0$であることに注意して、
\[\begin{align*}&\vec{c}\cdot\vec{d}=2\sqrt{6}\\\Leftrightarrow &\left(-\frac{2}{3}\vec{a}+\vec{b}\right)\cdot\vec{d}=2\sqrt{6}\\\Leftrightarrow &\vec{b}\cdot \vec{d}=2\sqrt{6}\\\Leftrightarrow &(2+2\sqrt{3})p+(2-2\sqrt{3})q-4=2\sqrt{6}\\\Leftrightarrow & (1+\sqrt{3})p+(1-\sqrt{3})q=2+\sqrt{6}\end{align*}\]
この2式を解いて、
\[p=\boldsymbol{1}+\frac{\sqrt{\boldsymbol{2}}}{\boldsymbol{2}},\,q=\boldsymbol{1}-\frac{\sqrt{\boldsymbol{2}}}{\boldsymbol{2}}\]
このとき、
\[\begin{align*}&\cos\angle\mathrm{COD}\\=&\frac{\vec{c}\vec{d}}{|\vec{c}||\vec{d}|}\\=&\frac{2\sqrt{6}}{2\sqrt{6}\cdot\sqrt{\left(1+\frac{\sqrt{2}}{2}\right)^2+\left(1-\frac{\sqrt{2}}{2}\right)^2+1^2}}\\=&\frac{1}{2}\end{align*}\]
であるので、$\angle\mathrm{COD}=\boldsymbol{60}^{\circ}$が分かります。
(4)
平面$\alpha$と平面$\beta$が垂直であり、$\angle\mathrm{COD}=60^{\circ}$であることから、四面体DABCの高さは、
\[|\vec{d}|\sin 60^{\circ}=\sqrt{\boldsymbol{3}}\]
となります。
底面である三角形ABCの面積は、先ほど求めた四角形OABCの面積から三角形OACの面積を引けば求まりますね。さらに、$\vec{a}\perp \vec{c}$であることも考慮すると、三角形ABCの面積は、
\[30-\frac{1}{2}|\vec{a}||\vec{c}|=12\]
となります。以上より、四面体DABCの体積は、
\[\frac{1}{3}\cdot 12\cdot \sqrt{3}=\boldsymbol{4}\sqrt{\boldsymbol{3}}\]
第5問(選択問題)
問題


解答
ア:1 イ:4 ウ:1 エ:2 オ:7 カ:4 キクケ:240 コサ:12 シス:02 セ:2 ソ:6 タチ:60 ツテ:30 トナ: 44 ニ:1 ヌネ:55 ノ:9
解説
(1)
\[E(X)=\frac{54\cdot 1 + 36\cdot 2 + 18\cdot 3}{720}=\frac{\boldsymbol{1}}{\boldsymbol{4}}\]
\[E(X^2)=\frac{54\cdot 1^2 + 36\cdot 2^2 + 18\cdot 3^2}{720}=\frac{\boldsymbol{1}}{\boldsymbol{2}}\]
ここで、分散$V(X)$と期待値についての公式
\[V(X)=E(X^2)-\{E(X)\}^2\]
を用いると、
\[V(X)=\frac{1}{2}-\left(\frac{1}{4}\right)^2=\frac{7}{16}\]
と分散が簡単に求まります。
分散のルートが標準偏差なので、
\[\sigma(X)=\frac{\sqrt{\boldsymbol{7}}}{\boldsymbol{4}}\]
(2)
$p=0.4$のとき、600人のうちの平均して4割が図書館を利用していることになるので、
\[E(Y)=600\cdot 0.4 =\boldsymbol{240}\]
また、分散は、
\[600p(1-p)=144\]
であるので、標準偏差はこのルートで、
\[\sigma(X)=\boldsymbol{12}\]
となります。
\[Z=\frac{Y-240}{12}\]
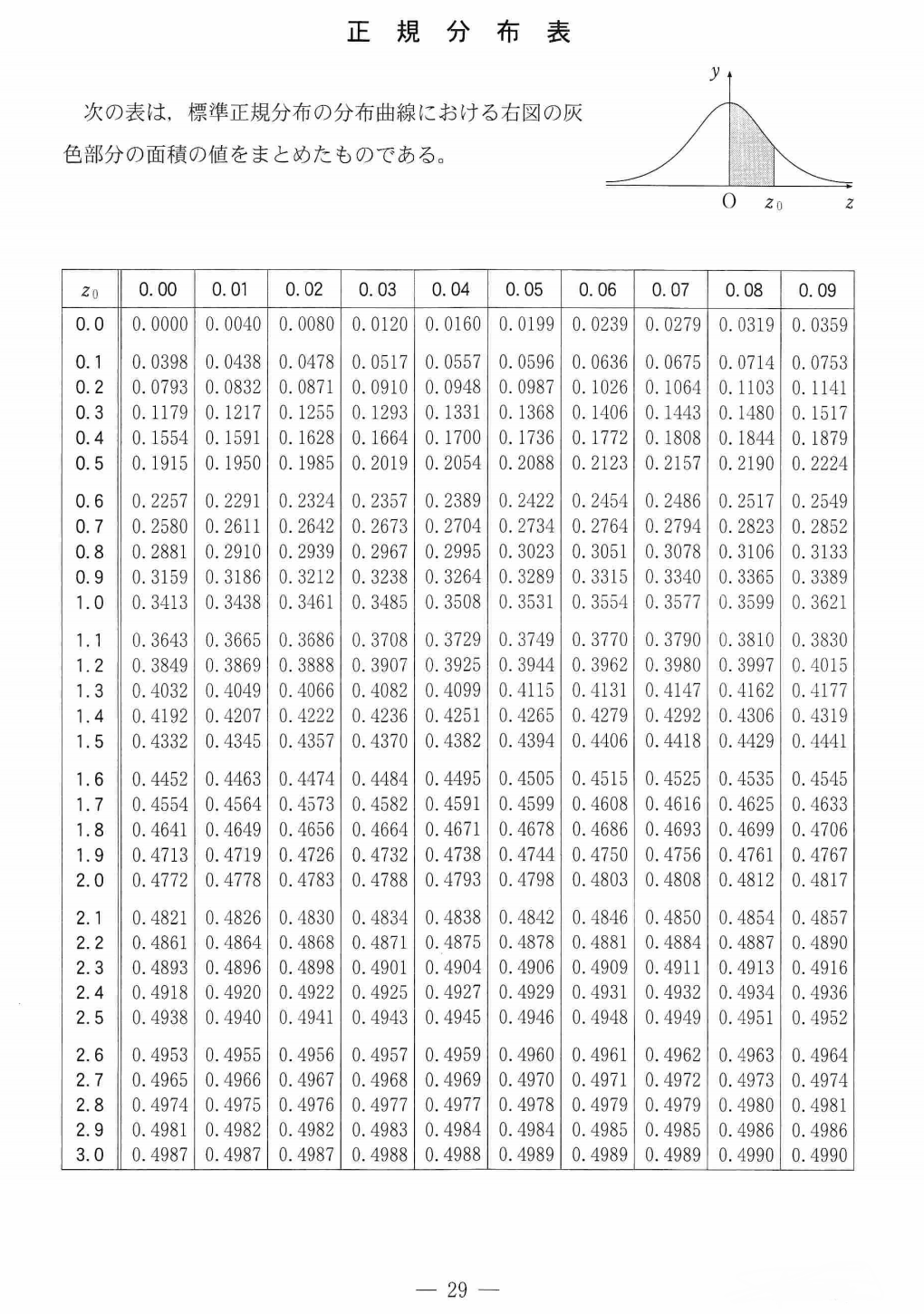
という変換をすると$Z$は標準正規分布に近似できるので、$y$が215以下となるのは、標準正規分布において、$\frac{215-240}{12}=-2.083\cdots$以下になる確率と等しいです。
正規分布表から$2.083$よりも大きくなる確率は、$0.5-0.4812=0.0188$くらいなので、正規分布の対称性から、$-2.083$以下になる確率もこの値になります。
四捨五入して、確率は$0.\boldsymbol{02}$となります。
$p=0.2$のときは、期待値は先ほどの$\frac{1}{\boldsymbol{2}}$倍となります。
また、標準偏差は、
\[\sqrt{600\cdot 0.2(1-0.2)}=4\sqrt{6}\]
となるので、$p=0.4$のときの$\frac{\sqrt{\boldsymbol{6}}}{3}$倍となります。
(3)
全部から60を引いたら当然期待値は60下がるので、
\[E(U_1)=\cdots =E(U_n)=m-\boldsymbol{60}\]
となります。グラフを左に60ずらしても標準偏差は変わらないので、
\[\sigma(U_1)=\cdots =\sigma(U_n)=\boldsymbol{30}\]
100人をサンプリングしたとき、標準誤差は、
\[\frac{30}{\sqrt{100}}=3\]
であるので、これを1.96倍したものを平均値に足し引きすれば95%信頼区間が求まりますね。
\[3\times 1.96 =5.88\]
であるので、
\[\boldsymbol{44.1}\leqq t\leqq \boldsymbol{55.9}\]
となります。



