2020年度のセンター試験(共通テスト)数学ⅡBの問題・解答・解説を見たい方はこちら
第1問(必答問題)
問題〔1〕
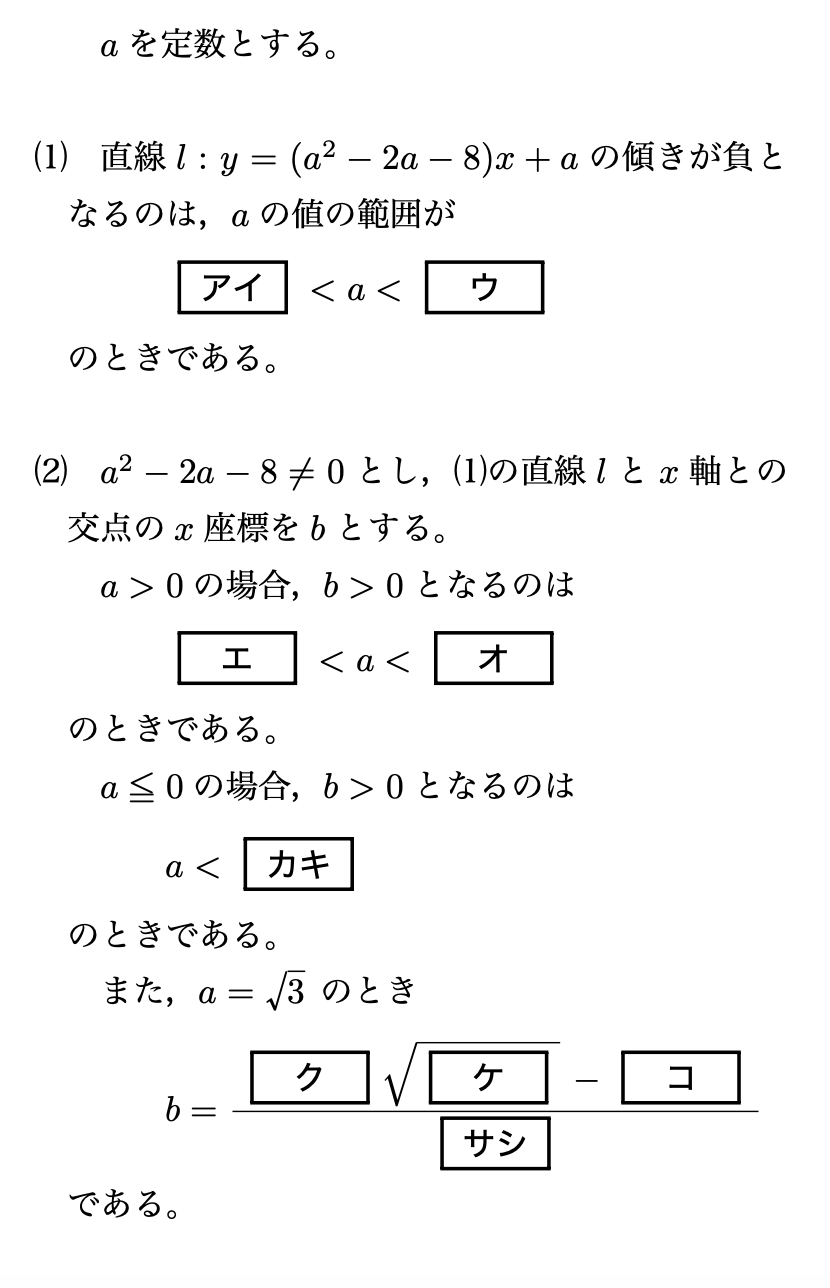
解答
アイ:-2 ウ:4 エ:0 オ:4 カキ:-2 ク:5 ケ:3 コ:6 サシ:13
解説
$a^2-2a-8=(a+2)(a-4)$と因数分解できるので、これが負になるのは、
\[\boldsymbol{-2<a<4}\]
のときです。
$x$切片は、
\[b=\frac{-a}{a^2-2a-8}\]
と書けるので、$a>0$の場合は分母である$a^2-2a-8$が負のとき、$a\leqq 0$の場合は分母である$a^2-2a-8$が正(でかつ$a\ne 0$)のとき、を求めてあげればOKです。
$a>0$のとき、
\[a^2-2a-8<0\Leftrightarrow -2<a<4\]
であり、場合分けの条件である$a>0$も考慮すると、
\[\boldsymbol{0<a<4}\]
となります。
$a\leqq 0$のとき、
\[a^2-2a-8>0\Leftrightarrow a<-2,\, 4<a\]
であり、場合分けの条件である$a\leqq 0$も考慮すると、
\[\boldsymbol{a<-2}\]
となります。
$a=\sqrt{3}$のときは、
\[b=\frac{-a}{a^2-2a-8}\]
に代入してあげて、
\[b= \boldsymbol{\frac{5\sqrt{3}-6}{13}}\]
と求まります。
問題〔2〕

解答
ス:2 セソ:12 タ:4 チ:3
解説
32は「4の倍数である」「6の倍数でない」「24の倍数でない」数なので、選択肢の中で$P,\,\overline{Q},\,\overline{R}$だけで構成された選択肢を選べばよいですね。よって、答えは、
\[\boldsymbol{P\cap\overline{Q}}\]
となります。
$P\cap Q$に属する自然数のうち最小のものというのは「4と6の最小公倍数」に等しいので、
\[\boldsymbol{12}\]
が答えになります。
12は24の倍数でないので、集合$R$に属しません。よって、
\[12\boldsymbol{\not \in}R\]
です。
これは「$P,\,Q$に属していても$R$に属するとは限らない」という例になっているので、
\[\boldsymbol{(pかつq)\Rightarrow r}\]
の反例になっています。
問題〔3〕
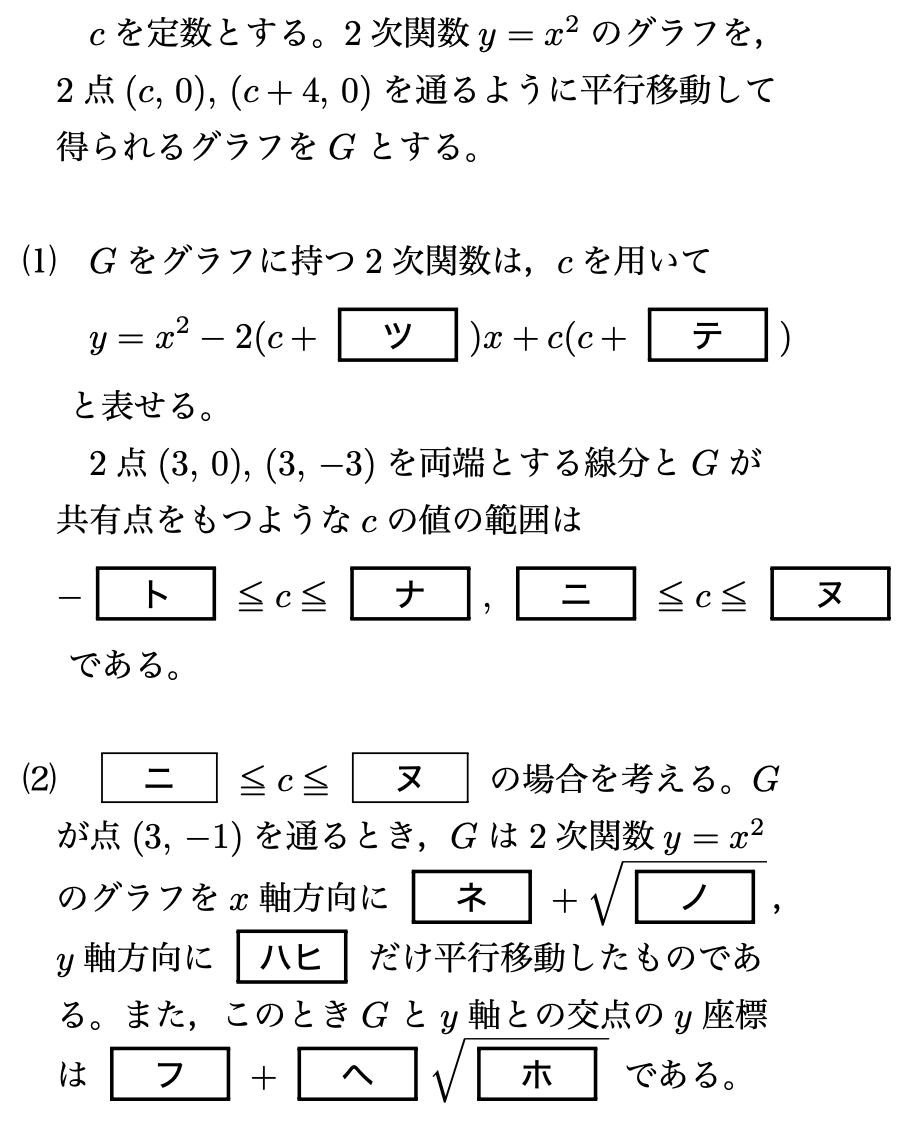
解答
ツ:2 テ:4 ト:1 ナ:0 ニ:2 ヌ:3 ネ:3 ノ:3 ハヒ:-4 フ:8 へ:6 ホ:3
解説
$x$軸との交点が$(c,\,0),\,(c+4,\,0)$ということは、
\[(x-c)\{x-(c+4)\}\]
と因数分解できるということなので、これを展開してあげて、
\[y=x^2-2(c+\boldsymbol{2})x+c(c+\boldsymbol{4})\]
となります。
2点$(3,\,0)$と$(3,\,-3)$を両端とする線分と$G$が共有点を持つというのは、「$x=3$のときのGの$y$座標が$-3$から$0$までの間にある」と言い換えることができるので、
\[-3\leqq 9-6(c+2)+c^2+4c \leqq 0\]
という不等式を解いてやればいいと分かります。
左側の不等式は、$c\leqq 0,\,2\leqq c$と解くことができて、
右側の不等式は、$-1\leqq c\leqq 3$と解くことができるので、これを合わせて、
\[\boldsymbol{-1\leqq c\leqq 0,\, 2\leqq c\leqq 3}\]
が答えとなります。
点$(3,\,-1)$を通るときは、$9-6(c+2)+c^2+4c=c^2-2c-3$が$-1$になるということなので、
\[c^2-2c-2=0\Leftrightarrow c=1\pm \sqrt{3}\]
このうち、$2\leqq c\leqq 3$を満たすのは、
\[c=1+\sqrt{3}\]
のみです。さて、$G$の式は、
\[y=\{x-(c+2)\}^2-4\]
と平方完成することができるので、$y=x^2$を$x$軸方向に$c+2$、$y$軸方向に$-4$だけ平行移動したグラフです。したがって、
\[x軸方向に\boldsymbol{3+\sqrt{3}}\]
\[y軸方向に\boldsymbol{-4}\]
平行移動したものだと言えます。
また、$y$切片は$c^2+4c$であるので、これに$c=1+\sqrt{3}$を代入して、
\[\boldsymbol{8+6\sqrt{3}}\]
となります。
第2問(必答問題)
問題〔1〕
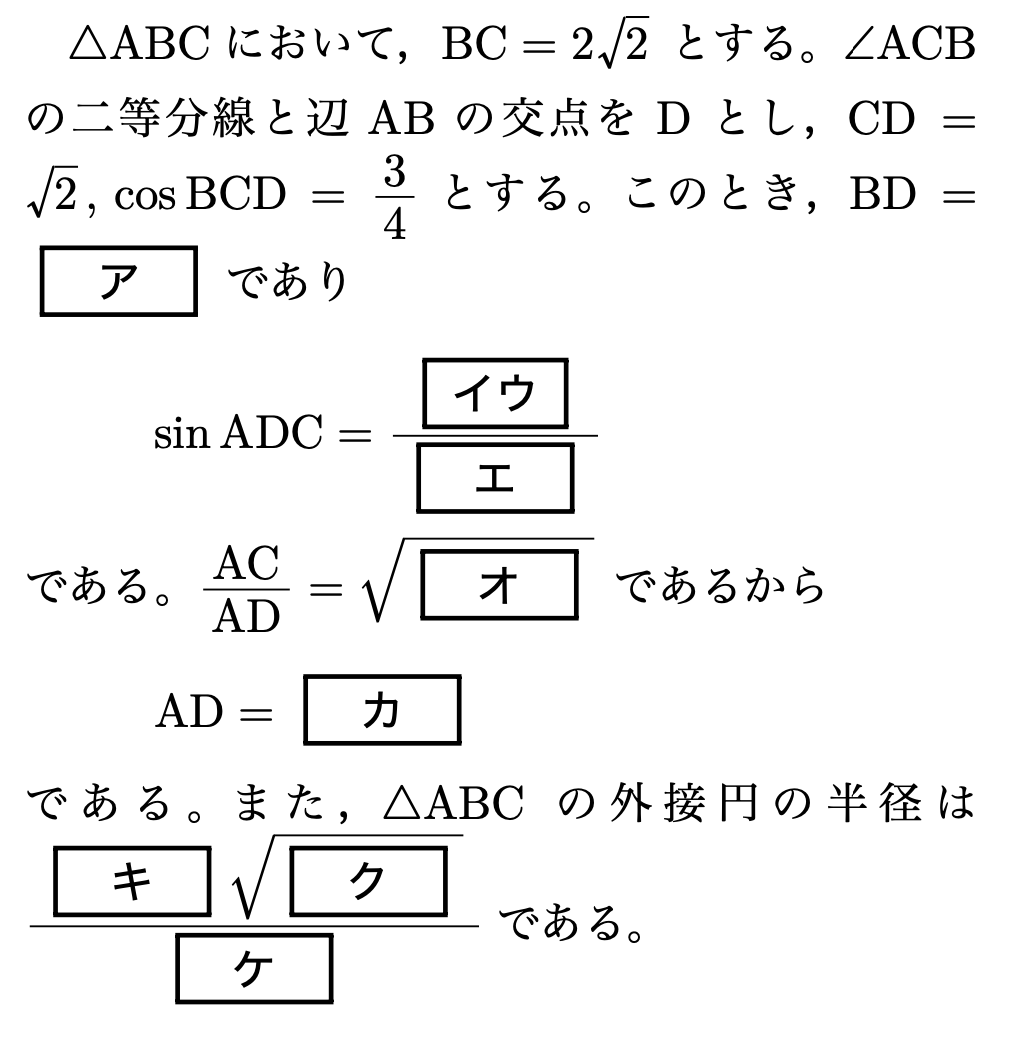
解答
ア:2 イウ:14 エ:4 オ:2 カ:1 キ:4 ク:7 ケ:7
解説
余弦定理から、
\[\cos \angle\mathrm{BCD}=\frac{\mathrm{BC}^2+\mathrm{CD}^2-\mathrm{BD}^2}{2\cdot\mathrm{BC} \cdot\mathrm{CD}}\]
が成り立つので、これに$\mathrm{BC}=2\sqrt{2}$、$\mathrm{BC}=\sqrt{2}$、$\cos \angle\mathrm{BCD}=\frac{3}{4}$を代入して、
\[\mathrm{BD}^2=4\]
辺の長さは正なので、
\[\mathrm{BD}=\boldsymbol{2}\]
となります。
よって、余弦定理より、
\[\cos \angle\mathrm{CDB}=\frac{\mathrm{DB}^2+\mathrm{DC}^2-\mathrm{BC}^2}{2\cdot\mathrm{DB}\cdot\mathrm{DC}}-\frac{1}{2\sqrt{2}}\]
が求まるので、$\sin$の2乗と$\cos $の2乗の和は$1$であり、$\sin\angle\mathrm{CDB}$の値は正であることを考えると、
\[\sin \angle\mathrm{CDB}=\frac{\sqrt{7}}{2\sqrt{2}}=\frac{\sqrt{14}}{4}\]
$\angle\mathrm{CDB}+\angle\mathrm{CDA}=180^{\circ}$より、$\sin\angle\mathrm{CDA}$の値はこれに等しく、
\[\sin\angle\mathrm{CDA}=\boldsymbol{\frac{\sqrt{14}}{4}}\]
角の2等分線の性質から、$\mathrm{BC}:\mathrm{BD}=\mathrm{AC}:\mathrm{AD}$が成り立つので、
\[\frac{\mathrm{AC}}{\mathrm{AD}}=\boldsymbol{\sqrt{2}}\]
となります。
この事実から、$\mathrm{AD}=x$とおくと、$\mathrm{AC}=\sqrt{2}x$と書けるので、余弦定理で式が立てられますね。余弦定理から、
\[\cos \angle\mathrm{ACD}=\frac{2+2x^2-x^2}{2\cdot \sqrt{2}\cdot\sqrt{2}x}\]
$\angle\mathrm{BCD}=\angle\mathrm{ACD}$であるので、$\cos \angle\mathrm{ACD}=\frac{3}{4}$を代入して、
\[x^2-3x+2=0\Leftrightarrow x=1,\,2\]
と、長さが2つ求まってしまいました。ここで、混乱してしまった受験生は少なくないと思われます。
冷静に何かもう一つ条件を考えてあげましょう。
例えば、先ほど求めた
\[\cos \angle\mathrm{CDB}=-\frac{1}{2\sqrt{2}}\]
を使えば、$\angle\mathrm{ADC}+\angle\mathrm{CDB}=180^{\circ}$であることより、
\[\cos \angle\mathrm{ADC}=\frac{1}{2\sqrt{2}}\]
だと分かります。$x=1,\,2$のそれぞれの場合について、$\cos \angle\mathrm{ADC}$を余弦定理から計算してみると、
\[x=1のとき\cos \angle\mathrm{ADC}=\frac{1}{2\sqrt{2}}\]
\[x=2のとき\cos \angle\mathrm{ADC}=-\frac{1}{2\sqrt{2}}\]
となるので、$x=1$のときのみ適することが分かります。したがって、
\[\boldsymbol{\mathrm{AD}=1}\]
だと分かります。
外接円の半径は正弦定理によって求めることができますね。余弦定理をもちいたあとに$\sin$を求める方法もしくは、数ⅡBの知識を使うのであれば倍角公式から、
\[\sin\angle\mathrm{ACB}=\frac{3\sqrt{7}}{8}\]
が分かるので、正弦定理より、外接円の半径を$R$とすると、
\[2R=\frac{3}{\frac{3\sqrt{7}}{8}}\]
\[R=\boldsymbol{\frac{4\sqrt{7}}{7}}\]
と求まります。
問題〔2〕



解答
コ:3 サ:5 (コとサは順不同) シ:6 ス:4 セ:3
解説
(1)四分位数に関する問題です。こういうときは極端な例を考えていけば簡単に間違っているものがわかります。
0.
1つだけが0で他の98個が100であるというデータを考えると、四分位数はどちらも100で、平均値は99.…になるので、誤っています。
1.
99個すべてが100のデータを考えると、標準偏差も四分位範囲も0になるので「より大きい」とは言えません。
2.
99個すべてが100のデータを考えると、中央値である100よりも小さいものは0個です。
3.
最大値を1つ削除しても、小さい方から25個目の観測値が第一四分位数になるので正しいです。
4.
99個すべてが100のデータを考えると、四分位数はどちらも100なので99個残ります。
5.
正しいです。
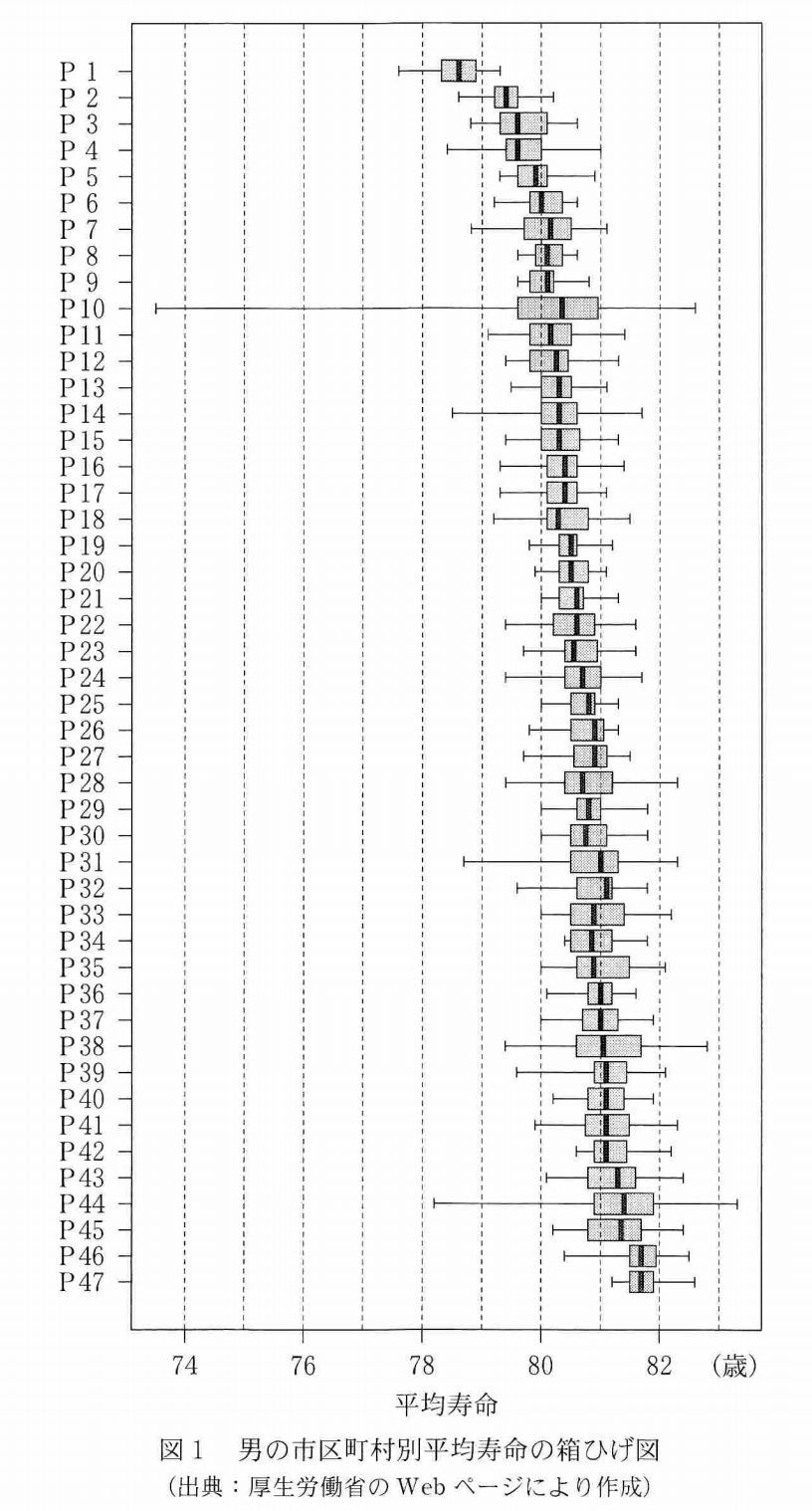
(2)都道府県のデータなので47個も箱ひげ図があることに焦ってしまった受験生が多いようですが、問題としては非常に易しいです。
まず、P10は四分位範囲(箱の部分の幅)が1より大きいので(Ⅰ)は誤りです。
次に、P32とP33では中央値がP32の方が大きくなっているので、(Ⅱ)も誤りです。
最後に、P1の最大値とP47の最小値には1.5以上の差があるので、(Ⅲ)も正しいです。
したがって、「誤・誤・正」である6が答えとなります。
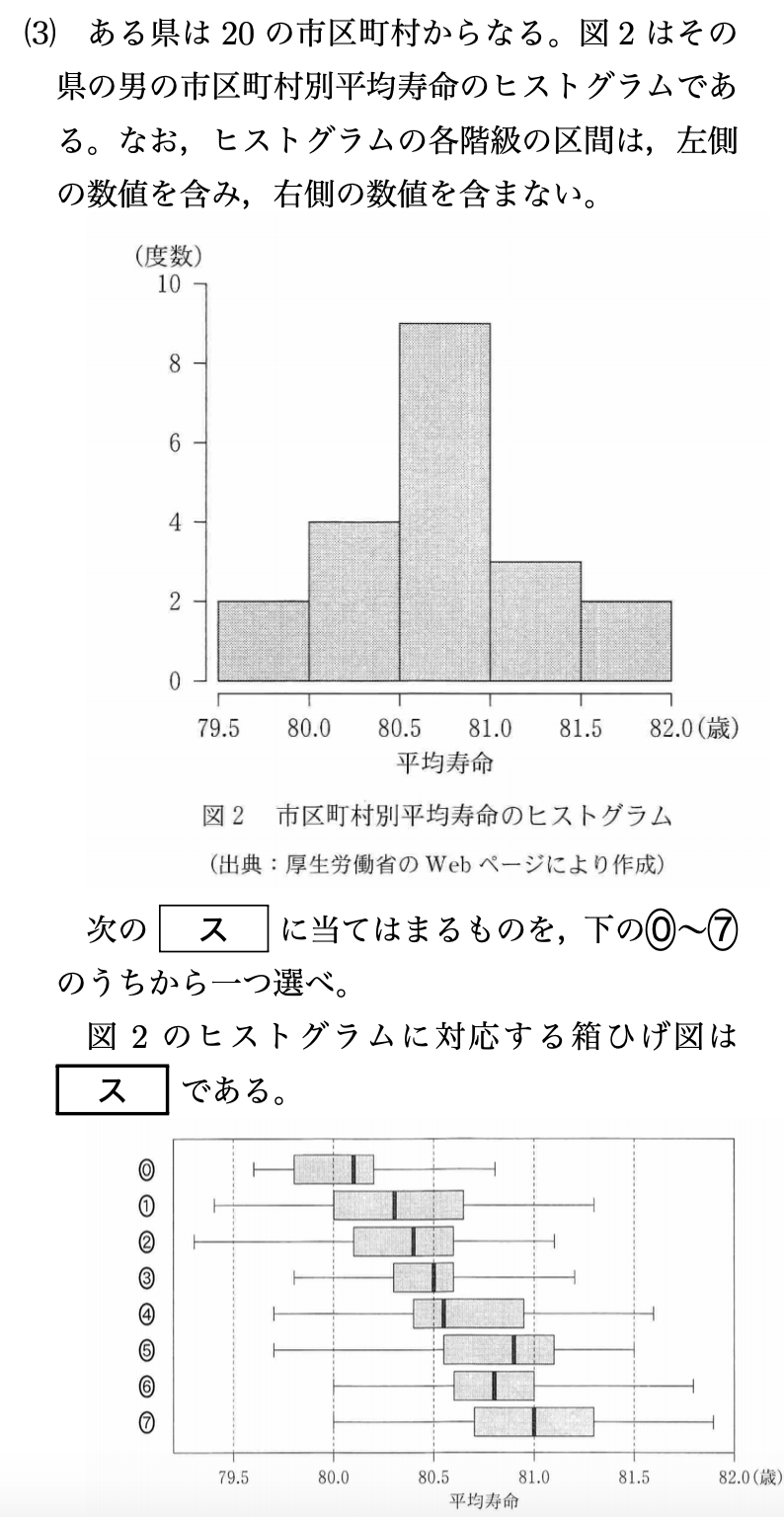
(3)ヒストグラムから「最小値は79.5〜80.0」「第一四分位数は80.0〜80.5」「中央値は80.5〜81.0」「最大値は81.5〜82.0」であることがわかるので、これをすべて満たす4が正解となります。
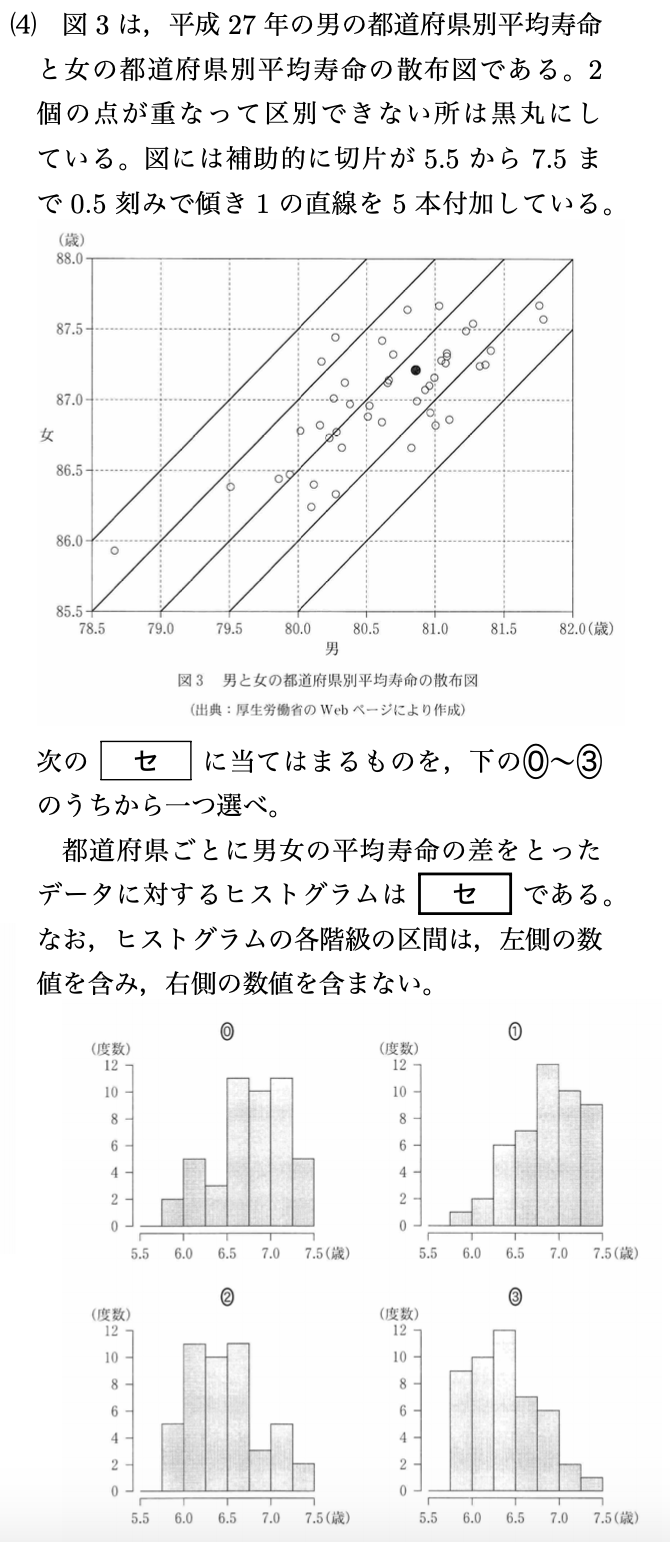
(4)5.5〜6までの範囲に9個データがあるので、これを唯一満たしている3が正解です。
第3問(選択問題)
問題〔1〕

解答
ア:0 イ:2 (アとイは順不同)
解説
0.
少なくとも1回表が出る確率は、すべて裏が出る確率を1から引けば求まるので、
\[1-\left(\frac{1}{2}\right)^5=0.96875>0.95\]
となり、正しいです。
1.
「1回コインを投げて表が出たから、このコインの表が出る確率は1だ!!」というくらい意味の分からないことを言っています。誤りです。
2.
書かれた文字が一致するのは、一回目に”ろ”か”は”のカードを引いて、次に一回目と同じひらがなが書かれたカードを引くときであるから、その確率は、
\[\frac{4}{5}\cdot\frac{1}{4}=\frac{1}{5}\]
です。1からこの値を引けば、書かれた文字が異なる確率となるので、
\[1-\frac{1}{5}=\frac{4}{5}\]
よって、正しいです。
3.
条件付き確率の問題です。この第3問全体として言えることなんですが「コインの表と裏が出る確率は等しい」という記述が欲しいかなと少し思いましたが、そうであるものとして計算していきます。
求めるべき条件付き確率は
\[\frac{コインが表でかつ2体のロボットが表と言う確率}{2体のロボットが表と言う確率}\]
です。
よって、
\[\frac{\frac{1}{2}\cdot 0.9\cdot 0.9}{\frac{1}{2}\cdot 0.9\cdot 0.9+\frac{1}{2}\cdot 0.1\cdot 0.1}=0.98\cdots\]
となるので、誤りです。
条件付き確率がよくわからないという人には以下の記事がおすすめです。
したがって、正解は0と2です。
問題〔2〕
解答
ウ:1 エ:4 オ:1 カ:2 キ:3 ク:3 ケ:8 コ:7 サシ:32 ス:4 セ:7
解説
2回コインを投げて-2点となるのは、裏が2回連続で出るときだけなので、
\[\left(\frac{1}{2}\right)^2=\boldsymbol{\frac{1}{4}}\]
です。-1点となるのは、表裏、裏表の2パターンあるので、
\[\left(\frac{1}{2}\right)^2\cdot 2=\boldsymbol{\frac{1}{2}}\]
となります。
0点になることが起こるのは、+2-1-1=0となるときすなわち、3回コインを投げたときで、0点になることが起こる確率は、表裏裏の並べ方に3パターンあることから、
\[\left(\frac{1}{2}\right)^3\cdot 3=\boldsymbol{\frac{3}{8}}\]
となります。
ゲーム終了時に持ち点が4点となるのは、+2+2+2-1-1=+4となるときです。この並べ方は10パターンありますが、ここで注意したいのが、先程考えた途中で0点になるパターンは除かなければならないということです。(例えば、表裏裏表表などはダメ)
よって、10-3=7パターンの並べ方があるので、
\[\left(\frac{1}{2}\right)^5\cdot 7=\boldsymbol{\frac{7}{32}}\]
となります。
2回までで持ち点が1となる場合は、最初の2回が表裏か裏表である場合のみで、さらに、途中で0点になってはいけないので、3回目は必ず表です。
残りの2回分は2パターンの出方があるので、結局4パターンの出方があります。したがって、分母は7パターン、分子は4パターンであるので、求める条件付き確率は、
\[\frac{\left(\frac{1}{2}\right)^5\cdot 4}{\left(\frac{1}{2}\right)^5\cdot 7}=\boldsymbol{\frac{4}{7}}\]
となります。
第4問(選択問題)
問題

解答
アイ:26 ウエ:11 オカ:96 キク:48 ケ:9 コサ:11 シス:36 セ:5 ソ:1 タ:6
解説
(1)
\[99x = 234\]
となるので、
\[x=\boldsymbol{\frac{26}{11}}\]
となります。
(2)
\[48y=2ab_{(7)}-2=98+7a+b-2\]
となるので、
\[y=\boldsymbol{\frac{96+7a+b}{48}}\]
だと分かります。
\[y=\frac{96+7a+b}{48}=2+\frac{7a+b}{48}\]
と変形できるので、$y$が分子が奇数で分母が4である分数に表されることは、$\frac{7a+b}{48}$が分子が奇数で分母が4である分数に表されることと等しいです。
$a,\,b$が$0$以上$6$以下の整数であることを考えると、題意を満たすのは、
\[7a+b=12,\,36\]
のときで、それぞれ、$(a,\,b)=(1,\,5),\,(5,\,1)$となるので、$a,\,b$は異なるという条件もたしかに満たしています。このときの$y$の値は、
\[y=\boldsymbol{\frac{9}{4},\,\frac{11}{4}}\]
となります。
$y=\frac{11}{4}$のときは$(a,\,b)=\boldsymbol{(5,\,1)}$、$7\times a+b=\boldsymbol{36}$です。
$y-2$は$\frac{7a+b}{48}$であるから、これが分子が1で分母が2以上の整数となるのは、「$7a+b$が$48$の約数のうち$48$以外と一致するとき」です。
よって、
\[7a+b=1,\,2,\,3,\,4,\,6,\,8,\,12,\,16,\,24\]
の9個の値が求まりますが、このうち、$a,\,b$は異なるという条件を満たすのは$7a+b=1,\,2,\,3,\,4,\,6,\,12$のときのみです。
したがって、全部で6個となります。
第5問(選択問題)
問題
解答
ア:1 イ:1 ウ:8 エ:2 オ:7 カ:9 キク:56 ケコ:12 サシ:72 ス:2
解説
チェバの定理やメネラウスの定理を使っていきます。
まず、三角形ABCと点Fについてチェバの定理から、
\[\frac{1}{7}\cdot \frac{7}{1}\cdot\frac{\mathrm{BG}}{\mathrm{AG}}=1\]
となるので、
\[\frac{\mathrm{BG}}{\mathrm{AG}}=\boldsymbol{1}\]
です。
次に、三角形ABDと直線CGについてメネラウスの定理より、
\[\frac{1}{1}\cdot \frac{1}{8}\cdot\frac{\mathrm{AF}}{\mathrm{FD}}=1\]
となるので、
\[\frac{\mathrm{FD}}{\mathrm{AF}}=\boldsymbol{\frac{1}{8}}\]
だと分かります。
続いて、三角形GBCと直線ADについてメネラウスの定理より、
\[\frac{2}{1}\cdot \frac{1}{7}\cdot \frac{\mathrm{GF}}{\mathrm{FC}}=1\]
となるので、
\[\frac{\mathrm{FC}}{\mathrm{GF}}=\boldsymbol{\frac{2}{7}}\]
と求まります。
以上の事実を用いれば、三角形CDGの面積は、三角形ABCの面積の$\frac{1}{2}\cdot\frac{1}{8}=\frac{1}{16}$倍であることが分かり、
また、三角形BGFの面積は、三角形ABCの面積の$\frac{1}{2}\cdot\frac{7}{9}=\frac{7}{18}$倍であることが分かるので、
\[\frac{\triangle \mathrm{CDG}の面積}{\triangle \mathrm{BFG}の面積}=\frac{\frac{1}{16}}{\frac{7}{18}}=\boldsymbol{\frac{9}{56}}\]
となります。
$\mathrm{FD}=1$のとき、
\[\frac{\mathrm{FD}}{\mathrm{AF}}=\frac{1}{8}\]
より、$\mathrm{AF}=8$が分かります。$\mathrm{AG}=x$とおくと、
\[\frac{\mathrm{BG}}{\mathrm{AG}}=1\]
より、$\mathrm{BG}=x$が言えます。よって、4点B、D、F、Gが同一円周上にあるとき、方べきの定理から、
\[\mathrm{AG}\cdot\mathrm{AB}=\mathrm{AF}\cdot\mathrm{AD}\]
が成り立つので、$x>0$であることに注意して、
\[x\cdot 2x = 8\cdot 9\Leftrightarrow x=6\]
と求まります。よって、ABはこの2倍で、
\[\mathrm{AB}=\boldsymbol{12}\]
です。
$\mathrm{AE}=3\sqrt{7}$とするとき、$\mathrm{AC}$の長さはこの$\frac{8}{7}$倍であることより、
\[\mathrm{AE}\cdot\mathrm{AC}=(3\sqrt{7})^2\cdot\frac{8}{7}=72\]
であり、これは先程計算した、$\mathrm{AG}\cdot\mathrm{AB}$の値と一致することに気づきます。そこで、方べきの定理の逆から、4点G、B、E、Cは同一円周上にあることが言えます。
円に内接する四角形の内対角の和は$180^{\circ}$になるという性質を用いれば、
\[\angle\mathrm{AEG}=\boldsymbol{\angle\mathrm{ABC}}\]
がすぐに分かります。



