東大医学部生の相談室

相加相乗平均の大小関係の証明や使い方、入試問題などを解説！

相加相乗平均の大小関係の証明や使い方、入試問題などを解説！

この記事を読むとわかること

・相加相乗平均の大小関係とは何か

・相加相乗平均の大小関係の視覚的な覚え方

・相加相乗平均の大小関係の一般化

・相加相乗平均の大小関係の証明

・相加相乗平均の大小関係の使い方や記述の書き方

・相加相乗平均の大小関係が関わる入試問題

目次

相加相乗平均の大小関係とは？

相加平均が相乗平均以上になる関係のこと

相加相乗平均の大小関係とは、2つの負でない数の相加平均が常に相乗平均以上になるという関係のことです。

数式的に書けば、$a\geqq 0,\,b\geqq 0$に対して、

\[\frac{a+b}{2}\geqq \sqrt{ab}\]

が常に成り立つという関係のことを指します。また、この不等式の等号が成り立つのは$a=b$の時のみであることも重要です。このような不等式の等号が成り立つような条件のことを一般に「等号成立条件」と言います。

 

また、“相加相乗平均の大小関係”と毎回書くのは面倒なので、説明の都合上、以下では”相加相乗”と略すことにします。

相加相乗は最大値や最小値を求める場面で頻出

相加相乗は最大値や最小値を求める場面で非常によく登場します。以下の例題を考えましょう。

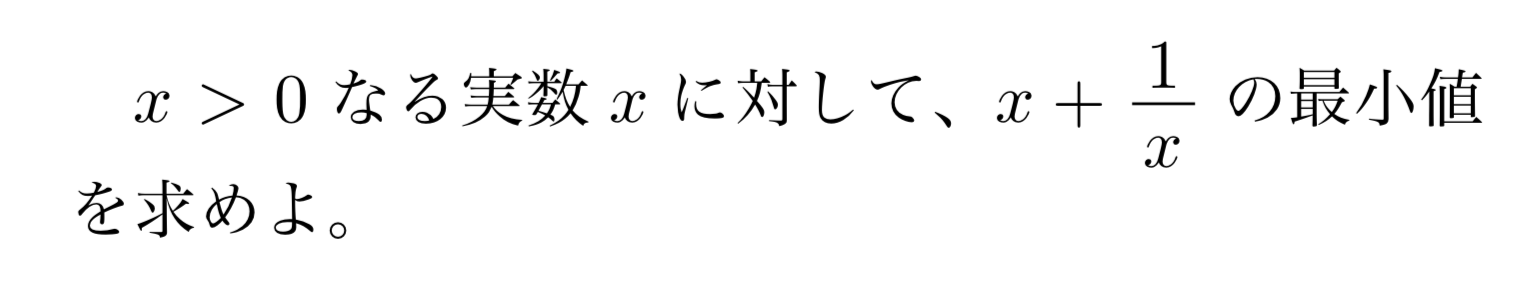
数Ⅲの微分を習っている人であれば、微分をしてしまえば最小値を求めることができますが、文系の人は相加相乗を使うことによって、最小値を求めることができます。

$x>0$より、$x$も$\frac{1}{x}$も正の数なので、相加相乗が使えて、

\[\frac{x+\frac{1}{x}}{2}\geqq \sqrt{x\cdot\frac{1}{x}}=1\]

つまり、

\[x+\frac{1}{x}\geqq 2\]

が常に成り立つことが言えます。ここで、等号成立条件は、

\[x=\frac{1}{x}かつx>0\Leftrightarrow x=1\]

となりますね。

したがって、$x=1$のときに最小値$2$を取ることが言えます。

 

このように、文系範囲では微分できない関数の最大値や最小値を求めるために相加相乗を使うというパターンの問題が入試では非常によく出題されます。

相加相乗の視覚的な覚え方

相加相乗を習ったばかりの人は、不等号の向きがどちらか、等号が成立するのはいつかなどをついつい間違えてしまいます。私は相加相乗の視覚的な覚え方を知ってからこのようなミスを全くしなくなりました！

その覚え方というのは以下の図です。

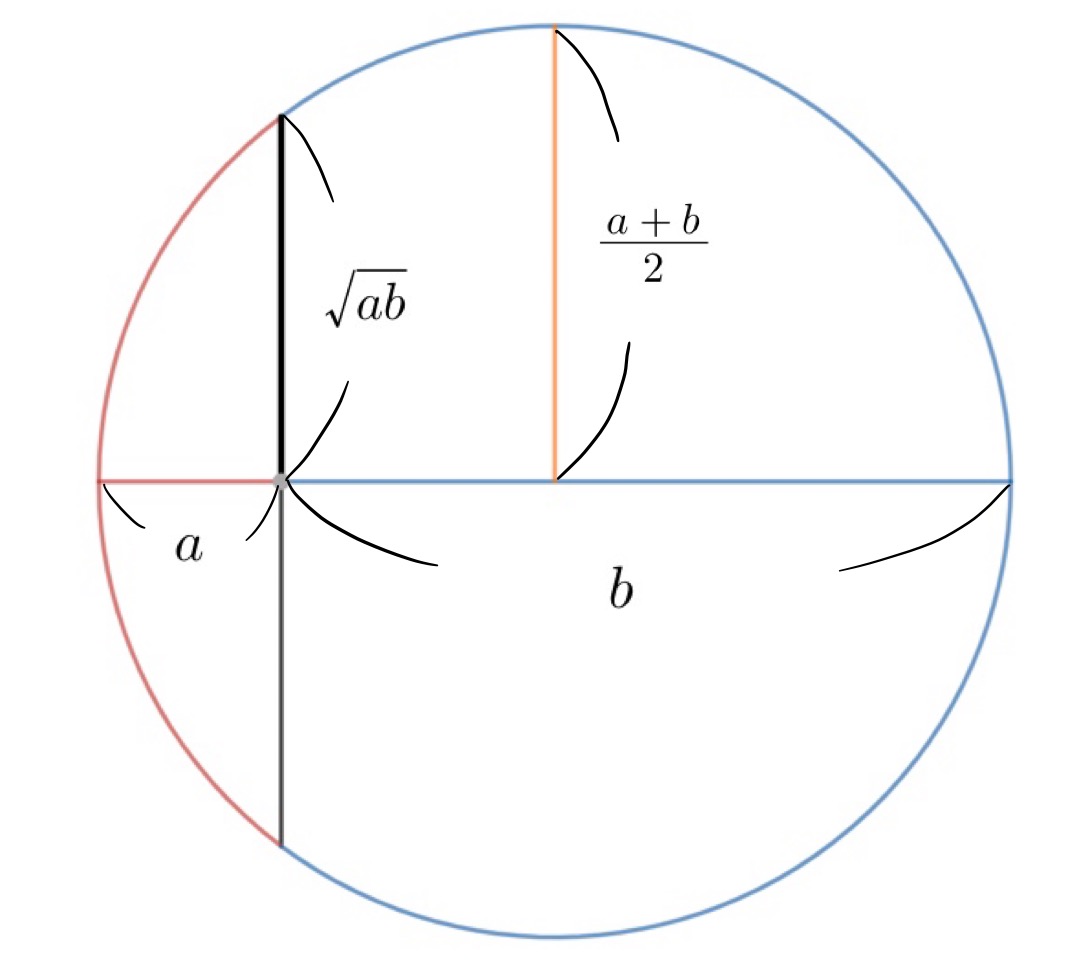
直径が$a+b$の円を考えたときに、半径は$a,\,b$の相加平均に、上図の黒太線の長さは相乗平均に等しくなります。相乗平均に等しくなることは、方べきの定理を用いることで簡単に確認できます。

上図の黒太線とその下の黒線は等しい長さなので、$x$とおけば、方べきの定理より、

\[x^2=ab\]

となるので、$x=\sqrt{ab}$が即座にわかります。

したがって、上図を見れば相加平均が相乗平均より必ず大きくなる(もしくは等しくなる)ことが視覚的に理解できますね！また、黒太線とオレンジ色の線がぴったり重なるのは、$a=b$のとき、つまり等号成立条件が$a=b$であることも視覚的にわかります。

相加相乗は一般化できる

相加相乗は以下の一般化されたものが成り立つことが知られています。

$n$個の$0$以上の数$a_1,\,a_2,\,\cdots,\,a_n$に対して、

\[\frac{a_1+a_2+\cdots+a_n}{n}\geqq \sqrt[n]{a_1\cdot a_2\cdots a_n}\]

が常に成り立つ。等号成立は、

\[a_1=a_2=\cdots =a_n\]

のとき。

n個の数の和をnで割ったものを「相加平均」、n個の数の積のn乗根を「相乗平均」と呼びます。”平均”と言っても色々な種類がありますが、「n個の数としてすべて同じものを選んだときにその数が出てくる」という性質を満たすことが必要です。

相加相乗の証明とは？

2文字の相加相乗の証明

相加相乗は簡単な式変形によって証明することができます。以下、証明です。

\[\frac{a+b}{2}-\sqrt{ab}=\frac{1}{2}(\sqrt{a}-\sqrt{b})^2\geqq 0\]

であるから、

\[\frac{a+b}{2}\geqq \sqrt{ab}\]

が示された。また、等号成立は、$a\geqq 0,\,b\geqq 0$より、

\[\sqrt{a}=\sqrt{b}\Leftrightarrow a=b\]

のときである。

一般化された相加相乗の証明

相加相乗の一般化された形を証明するのはかなり大変です。証明の手法としては以下の2種類があります。

相加相乗の一般化されたものの証明のしかた

1.数学的帰納法による証明

2.$\boldsymbol{e^x\geqq 1+x}$を利用した証明

数学的帰納法による証明については、以下の記事で双方向帰納法の説明に出てくるので興味のある人は読んでみてください。

数学的帰納法とは？入試問題付きで全5パターンをわかりやすく解説！

ここでは、最も鮮やかに証明できる2の手法を紹介したいと思います。数Ⅲ範囲の知識を使っているので、数Ⅲがよくわからないという人は読み飛ばしてしまって構いません。

$a_1,\,a_2,\,\cdots ,\,a_n$の相加平均を$M$、$a_1,\,a_2,\,\cdots ,\,a_n$をすべてかけ合わせたものを$N$と表記する。

$e^x\geqq 1+x$に$x=\frac{a_k}{M}-1(k=1,\,2,\,\cdots,\,n)$を代入すると、

\[e^{\frac{a_k}{M}-1}\geqq\frac{a_k}{M}\]

となる。これを$k=1,\,2,\,\cdots,\,n$について作り、各辺すべて$0$以上であることに注意して片々掛け合わせると、

\begin{align*}&e^{\frac{\sum_{k=1}^{n}a_k}{M}-n}\geqq\frac{N}{M^n}\\\Leftrightarrow &e^0\geqq \frac{N}{M^n}\\\Leftrightarrow &M\geqq \sqrt[n]{N}\end{align*}

したがって、

\[\frac{a_1+a_2+\cdots+a_n}{n}\geqq \sqrt[n]{a_1\cdot a_2\cdots a_n}\]

が示された。

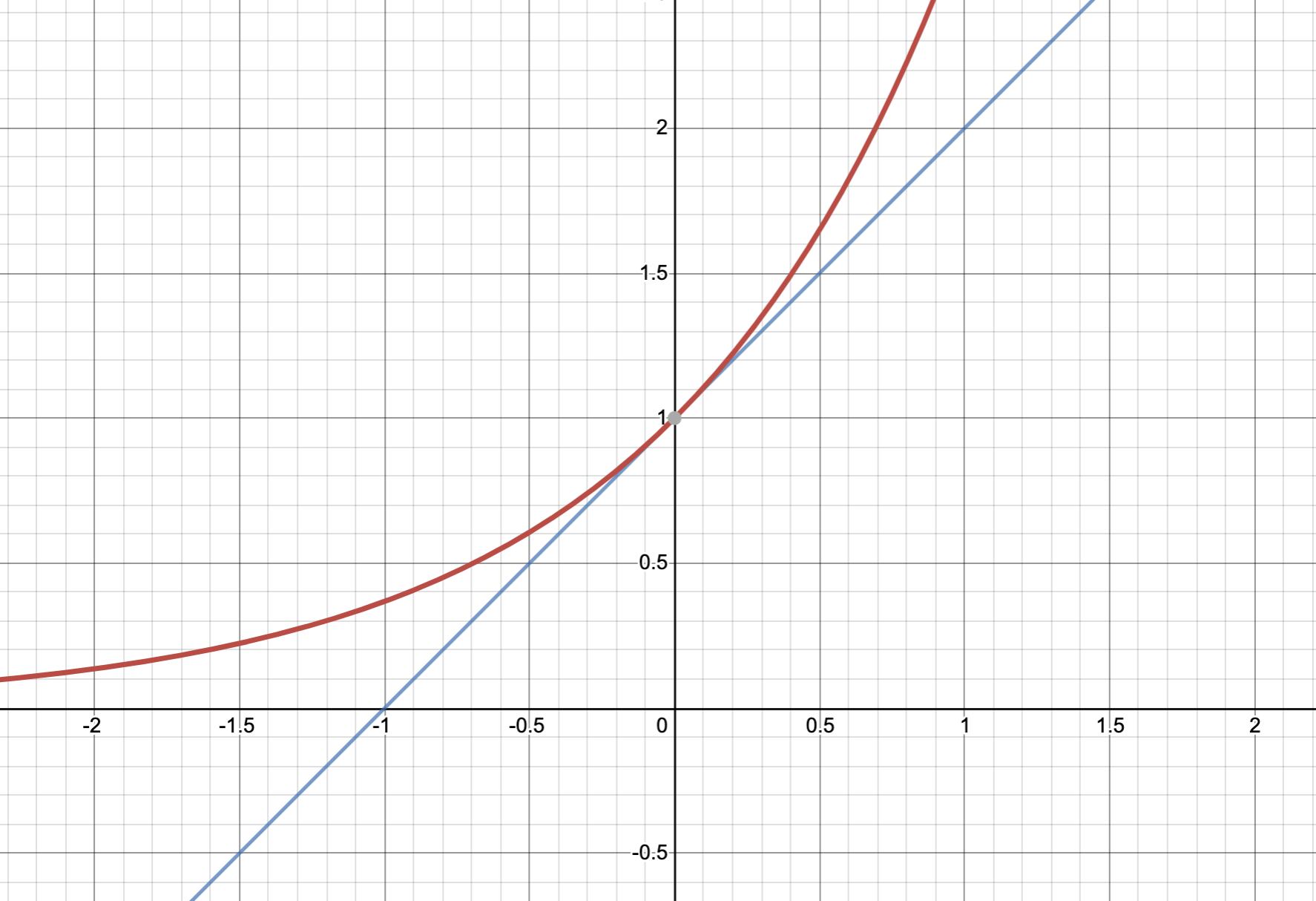
はじめに用いた不等式は、微分すればすぐに確かめられます。$y=e^x$と$y=x+1$のグラフを描くと一目でわかりますね。

相加相乗の使い方・記述の書き方

相加相乗を数学の答案で使うときにはどのようなことに気をつけて、どのような記述の書き方をすればよいのでしょうか？

相加相乗を使う時には必ず以下の3点に注意する必要があります。

相加相乗を使うときの注意点3つ！

1.2数が0以上であるかを確認する

2.等号成立条件をチェックする

3.定数でおさえる

先ほども用いた以下の例題を用いながら、それぞれについて説明していきます。

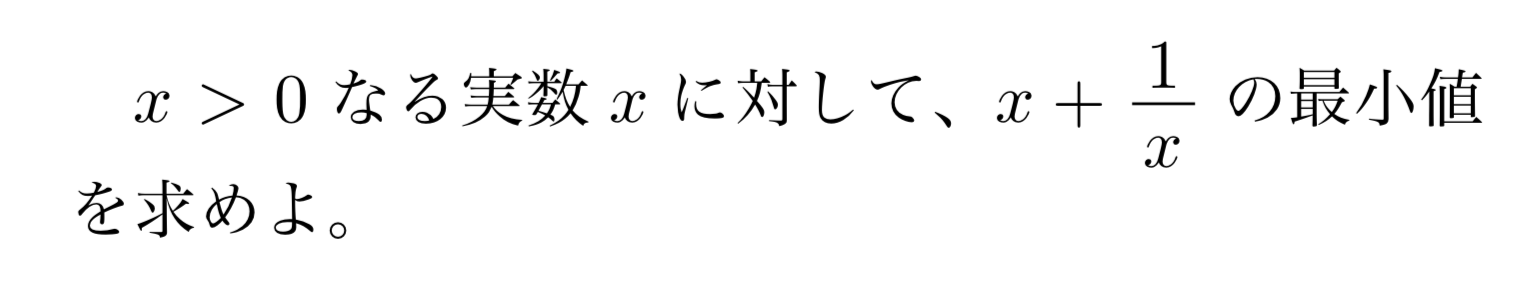
2数が0以上であるかを確認する

相加相乗はいつでも使えるわけではないです。「$a\geqq 0,\,b\geqq 0$に対して」成り立つ不等式なので、相加相乗を用いるときには、これが満たされているかどうかをチェックする必要があります。

よって、上の例題であれば、

$x>0$より、$x>0$かつ$\frac{1}{x}>0$であるから、相加相乗平均の大小関係より、

\[x+\frac{1}{x}\geqq 2\]

と記述で書く必要があります。

これは受験生がついつい忘れがちなところなので注意しましょう。

等号成立条件をチェックする

相加相乗を使ったからといってその値が最大値や最小値になっているとは限らないことに注意しましょう。等号成立条件をチェックする記述を書く必要があります。

上の例題であれば、

等号成立は、

\[x=\frac{1}{x}かつx>0\Leftrightarrow x=1\]

と書けばOKですね。この等号成立のときが求まらなければ、不等式自体は正しくても2という値が最小値だとは言えなくなってしまいます。(例えば与えられた条件が$x>0$ではなく$x\geqq 2$だったら最小値は$\frac{5}{2}$になりますよね。)

定数でおさえる

相加相乗は最大値や最小値を求めるために用いますが、このとき定数でおさえられていなければ意味がないことに注意してください。

上の例題とは別に、以下の例題について相加相乗を用いて最小値を求める記述を書いてみます。以下の記述は誤っているんですが、どこが誤っているかわかりますか？

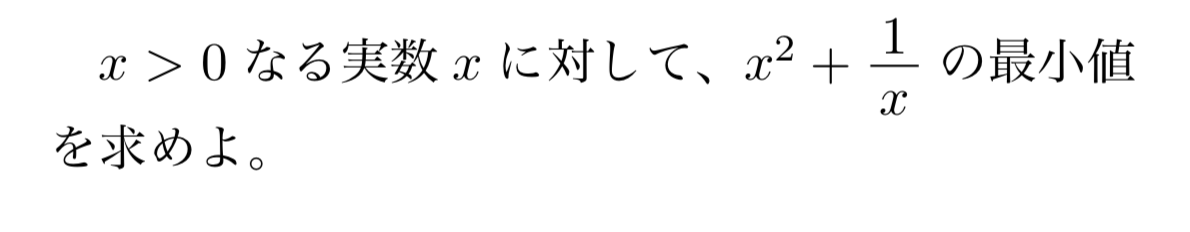
誤答例

$x>0$より$x^2>0$かつ$\frac{1}{x}>0$であるから、相加相乗平均の大小関係より、

\[x^2+\frac{1}{x}\geqq 2\sqrt{x}\]

等号成立は、

\[x^2=\frac{1}{x}かつx>0\Leftrightarrow x=1\]

のとき。これを代入して、最小値は、

\[\boldsymbol{2(x=1のとき)}\]

相加相乗が使える条件をチェックしてから等号成立条件もチェックしているので、一見正しそうに見えますが、グラフを描いて考えてみるとこれが最小値を求める作業には全くなっていないことがわかります。

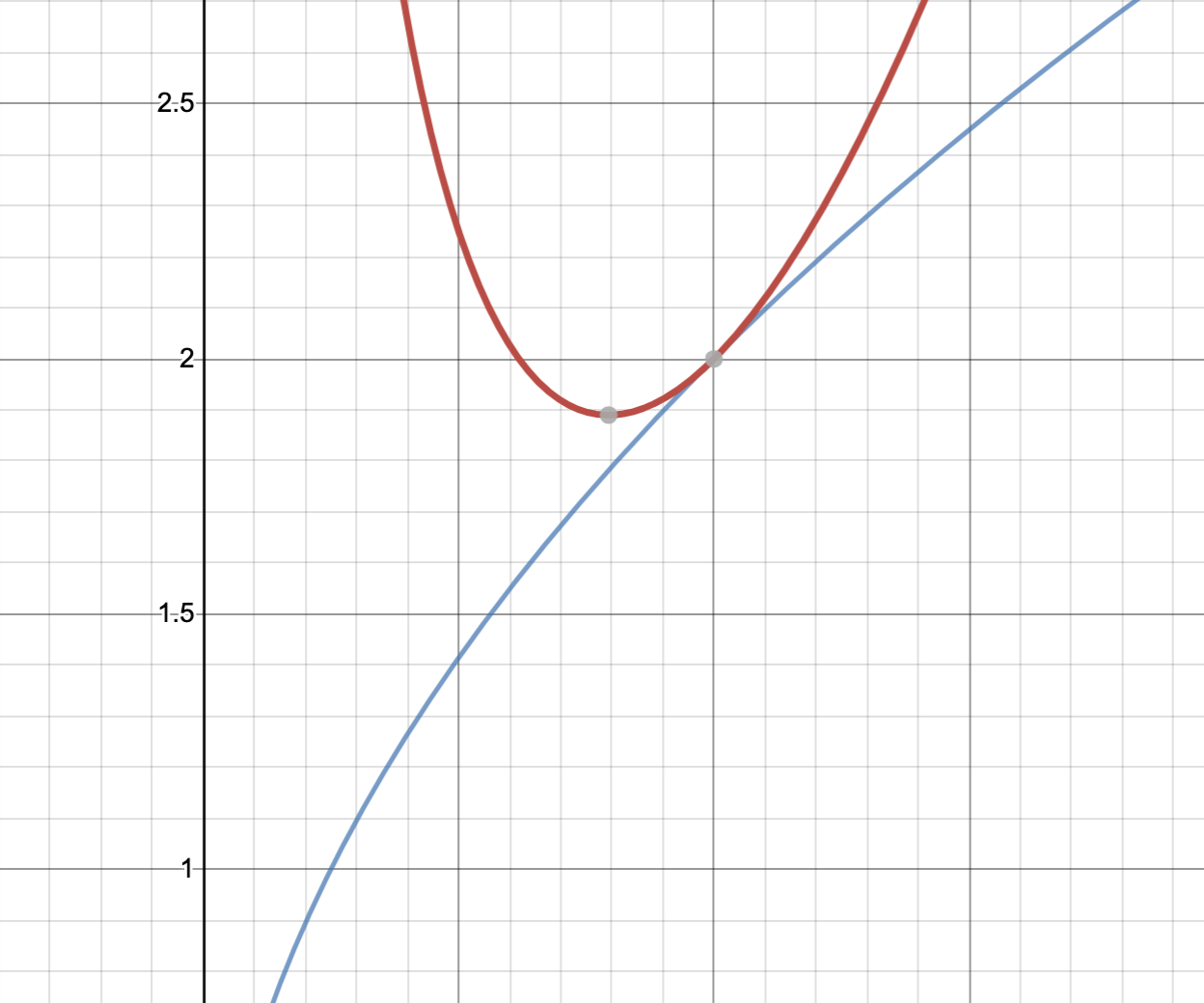
赤のグラフが$y=x^2+\frac{1}{x}$で青のグラフが$y=2\sqrt{x}$のグラフです。先ほどの誤答例の中で相加相乗を使って示せたのは、「$y=x^2+\frac{1}{x}$のグラフが常に$y=2\sqrt{x}$のグラフよりも上にあって、かつ、それらが接する時は$x=1$のとき。」ということなんですね。これを示したところで最小値は求めたことにはなっていませんよね。

このように、相加相乗を使ったあとに定数でおさえることができていないと、最大値や最小値を求める議論には全くならないことがわかります。定数でおさえるために以下のように変形を施して、3文字の相加相乗を使うことで正しい答案が出来上がります。

\[x^2+\frac{1}{x}=x^2+\frac{1}{2x}+\frac{1}{2x}\]

$x>0$より$x^2>0$かつ$\frac{1}{2x}>0$であるから、相加相乗平均の大小関係より、

\[x^2+\frac{1}{2x}+\frac{1}{2x}\geqq \frac{3}{\sqrt[3]{4}}\]

等号成立は、

\[x^2=\frac{1}{2x}=\frac{1}{2x}かつx>0\Leftrightarrow x=\frac{1}{\sqrt[3]{2}}\]

のとき。したがって、求める最小値は、

\[\boldsymbol{\frac{3}{\sqrt[3]{4}}\left(x=\frac{1}{\sqrt[3]{2}}のとき\right)}\]

この場合はしっかりと$\frac{3}{\sqrt[3]{4}}$という定数でおさえられてますね！ここが注意できていないと訳のわからない答案を書くことになってしまうので気をつけましょう。

相加相乗が関わる入試問題5選

相加相乗を使う入試問題を5つ紹介したいと思います！

基礎的な問題から東大の入試問題まで入っているので、ぜひ取り組んでみてください。また、先ほど挙げた記述を書く時の注意点などが押さえられているかどうかにも気をつけてくださいね。

問題1

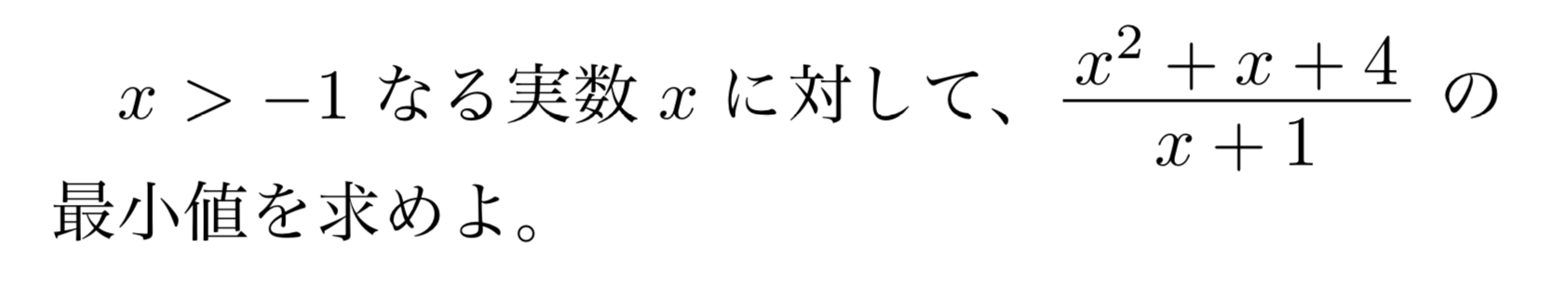
解答・解説

まず、与えられた分数式は、分母よりも分子の方が次数になっていますね。こういった分数式は、次数下げをして、分子の次数の方が小さくなるようにしておくのが鉄則です。

分母の次数よりも分子の次数が大きい分数式は、次数下げをして、分子の次数の方が小さくなるようにする！

よって、今回の問題であれば、

\[\frac{x^2+x+4}{x+1}=x+\frac{4}{x+1}\]

と変形するのがまずやるべきことです。さらに、ここから相加相乗の利用を考えたいところですが、このまま相加相乗を用いても、

\[x+\frac{4}{x+1}\geqq 2\sqrt{\frac{4x}{x+1}}\]

となり、定数でおさえることができません。そこで、「定数でおさえることができるように、無理やり$x+1$を作り出す」という作業が必要になります。

以下、解答例です。

\[\frac{x^2+x+4}{x+1}=x+\frac{4}{x+1}=x+1+\frac{4}{x+1}-1\]

ここで、$x>-1$より、$x+1>0$かつ$\frac{4}{x+1}$であるから、相加相乗平均の大小関係より、

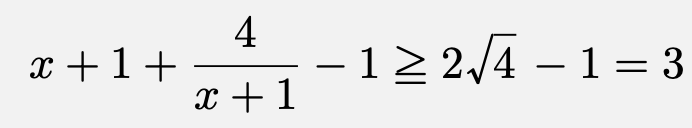
等号成立は、

\[x+1=\frac{4}{x+1}かつx>-1\Leftrightarrow x=1\]

のとき。

したがって、求める最小値は、

\[\boldsymbol{3(x=1のとき)}\]

問題2

解答・解説

今まで相加相乗の利用のしかたとして最小値を求める場合しか見せていませんでしたが、最大値を求めることに使うことも多いです。

与えられた分数式は常に正なので、逆数が最小値を取る時に元の式が最大になりますよね。逆数をとって次数下げしてみると、相加相乗が使える形になっていることに気づくので、これで解けますね！

逆数の最小値を相加相乗で求めて、最大値が求まるケースも多い！

以下、解答例です。

\[\frac{x}{x^2-x+4}=\frac{x}{\left(x-\frac{1}{2}\right)^2+\frac{7}{2}}\]

より、$x>0$においてこれは常に正の値を取る。よって、逆数が最小になるときにこれは最大になる。

\[\frac{x^2-x+4}{x}=x+\frac{4}{x}-1\]

$x>0$より、$x>0$かつ$\frac{4}{x}>0$であるので、相加相乗平均の大小関係より、

\[x+\frac{4}{x}-1\geqq 2\sqrt{4}-1=3\]

等号成立は、

\[x=\frac{4}{x}かつx>0\Leftrightarrow x=2\]

したがって、逆数の最小値は$3$であるので、求める最大値は、

\[\boldsymbol{\frac{1}{3}(x=2のとき)}\]

問題3

解答・解説

2変数関数の最大最小問題になっています。多変数関数の最大最小問題は以下のような手順で解くのでした。

多変数関数の最大最小問題

1.等式条件があれば文字消去に使う

2.等式条件がない、もしくは、文字消去しても2文字以上の関数の場合

a.文字固定

b.図示

c.同次式

d.有名不等式

今回は、分母も分子も2次の同次式(すべての項が2次になっている式のこと)になっているので、同次式であることに注目して、$\frac{x}{y}$の1文字の式に変換することができます。

1文字の式になれば、先ほどの問題1や問題2のように相加相乗が使える形になるので、最大値が求まりそうですね。

以下、解答例です。

$y>0$より、与式の分母分子を$y^2$で割ることができて、

\[\frac{\left(\frac{x}{y}\right)^2+\frac{x}{y}+1}{\left(\frac{x}{y}\right)^2-\frac{x}{y}+1}\]

ここで、$t=\frac{x}{y}$とおくと、$x,\,y$は正の実数値を自由に取れるので、$t$の変域は$t>0$であり、

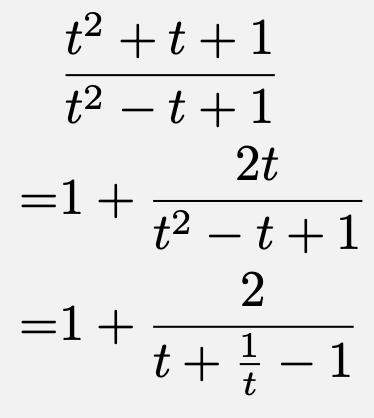
\begin{align*}&\frac{t^2+t+1}{t^2-t+1}\\=&1+\frac{2t}{t^2-t+1}\\=&1+\frac{2}{t+\frac{1}{t}-1}\end{align*}

$t>0$より、相加相乗平均の大小関係から、

\[1+\frac{2}{t+\frac{1}{t}-1}\leqq 1+\frac{2}{2-1}=3\]

等号成立は、

\[t=\frac{1}{t}かつt>0\Leftrightarrow t=1\Leftrightarrow x=y\]

以上より、求める最大値は、

\[\boldsymbol{3(x=yのとき)}\]

問題2のように逆数の最小値が求まるので、元の数の最大値が求まるパターンですが、逆数を取る記述は面倒なので、上のように$t$で約分して分母に対して相加相乗を適用するとよいでしょう。

問題4

解答・解説

図形と絡めた最大最小問題です。角度が等しいという条件が与えられていますが、直線の傾きの情報が与えられているとして処理すればよいでしょう。

点$\mathrm{D}$の座標を$t$で表せたら、あとは三角形$\mathrm{ACD}$の面積も簡単に$t$で表せますね。ここで相加相乗が使えます。

以下、解答例です。

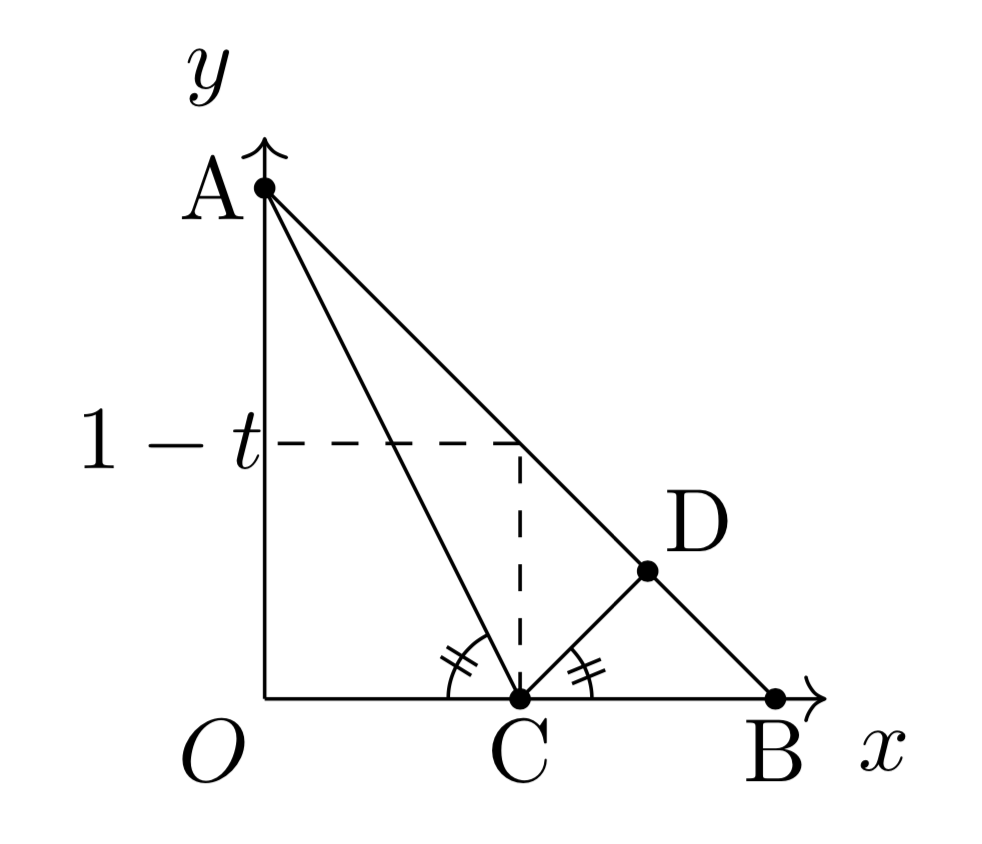
直線$\mathrm{AC}$の傾きは$-\frac{1}{t}$であり、$\angle\mathrm{ACO}=\angle\mathrm{BCD}$であるから、直線$\mathrm{CD}$の傾きは$\frac{1}{t}$である。よって、点$\mathrm{D}$は、直線$y=-x+1$と$y=\frac{1}{t}(x-t)$の交点である。

\[\left\{\begin{array}{l}y=-x+1\\y=\frac{1}{t}(x-t)\end{array}\right.\Leftrightarrow(x,\,y)=\left(\frac{2t}{1+t},\,\frac{1-t}{1+t}\right)\]

であるから、点$\mathrm{D}$の座標は$\left(\frac{2t}{1+t},\,\frac{1-t}{1+t}\right)$である。よって、三角形$\mathrm{ACD}$の面積は、

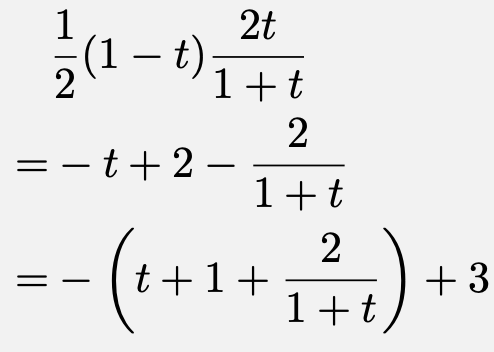
\begin{align*}&\frac{1}{2}(1-t)\frac{2t}{1+t}\\=&-t+2-\frac{2}{1+t}\\=&-\left(t+1+\frac{2}{1+t}\right)+3\end{align*}

となる。ここで、$t>0$より、$t+1>0$かつ$\frac{2}{1+t}>0$であるから、相加相乗平均の大小関係より、

\[-\left(t+1+\frac{2}{1+t}\right)+3\leqq -2\sqrt{2}+3\]

等号成立は、

\[t+1=\frac{2}{1+t}かつ0<t<1\Leftrightarrow t=\sqrt{2}-1\]

のとき。したがって、求める最大値は、

\[\boldsymbol{3-2\sqrt{2}(t=\sqrt{2}-1のとき)}\]

問題5

解答・解説

ベクトルを用いた立体の体積の最大最小問題です。(1)では、式を変形して代入したあと、3つのベクトルが1次独立であることに注目することで解けます。(2)では、垂線を扱うことになりますが、平面と垂直であるという条件は、その平面に平行で互いに1次独立な2つのベクトルとの内積が0であるという条件で扱うのでした。

(2)から$\overrightarrow{\mathrm{RH}}$の長さが求められるので、三角形$\mathrm{OPQ}$を底面と見て、三角錐の体積が求められます。あとは、(1)の条件下での体積の最小値を求めることになりますが、このときに相加相乗が使えます。

以下、解答例です。

(1)\[\overrightarrow{\mathrm{OA}}=\frac{1}{p}\overrightarrow{\mathrm{OP}},\,\overrightarrow{\mathrm{OB}}=\frac{1}{q}\overrightarrow{\mathrm{OQ}},\,\overrightarrow{\mathrm{OC}}=\frac{1}{r}\overrightarrow{\mathrm{OR}}\]

を$4\overrightarrow{\mathrm{OG}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}$に代入すると、

\[\overrightarrow{\mathrm{OG}}=\frac{1}{4p}\overrightarrow{\mathrm{OP}}+\frac{1}{4q}\overrightarrow{\mathrm{OQ}}+\frac{1}{4r}\overrightarrow{\mathrm{OR}}\]

となる。ここで、$\overrightarrow{\mathrm{OP}},\,\overrightarrow{\mathrm{OQ}},\,\overrightarrow{\mathrm{OR}}$は1次独立であるので、点$\mathrm{G}$が平面$\mathrm{PQR}$上にあるための条件は、

\[\frac{1}{4p}+\frac{1}{4q}+\frac{1}{4r}=1\Leftrightarrow \frac{1}{p}+\frac{1}{q}+\frac{1}{r}=4\]

したがって、題意成立。

(2)　$\overrightarrow{\mathrm{OH}}$は平面$\mathrm{OAB}$の点であるので、実数$s,\,t$を用いて、$\overrightarrow{\mathrm{OH}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}$と書ける。$\overrightarrow{\mathrm{RH}}$は平面$\mathrm{OAB}$に対して垂直であるから、

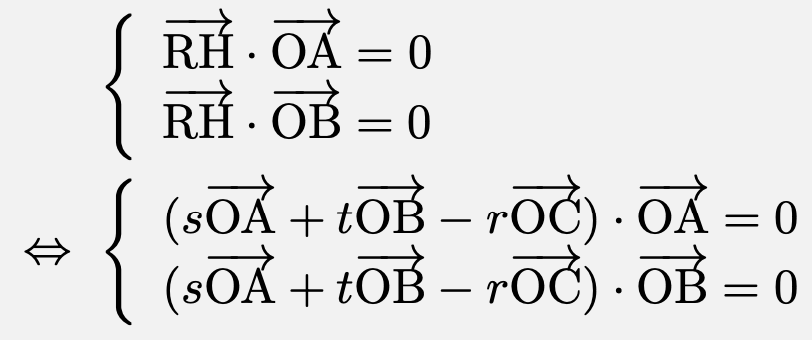
\begin{align*}&\left\{\begin{array}{l}\overrightarrow{\mathrm{RH}}\cdot\overrightarrow{\mathrm{OA}}=0\\\overrightarrow{\mathrm{RH}}\cdot\overrightarrow{\mathrm{OB}}=0\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}(s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}-r\overrightarrow{\mathrm{OC}})\cdot\overrightarrow{\mathrm{OA}}=0\\(s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}-r\overrightarrow{\mathrm{OC}})\cdot\overrightarrow{\mathrm{OB}}=0\end{array}\right.\end{align*}

$\left|\overrightarrow{\mathrm{OA}}\right|=\left|\overrightarrow{\mathrm{OB}}\right|=\left|\overrightarrow{\mathrm{OC}}\right|=1$、$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{OC}}\cdot\overrightarrow{\mathrm{OA}}=\frac{1}{2}$であることより、

\[\left\{\begin{array}{l}s+\frac{1}{2}t+\frac{1}{2}r=0\\\frac{1}{2}s+t+\frac{1}{2}r=0\end{array}\right.\Leftrightarrow (s,\,t)=\left(\frac{r}{3},\,\frac{r}{3}\right)\]

となるので、題意成立。

(3)　三角錐$\mathrm{OPQR}$について、三角形$\mathrm{OPQ}$を底面と見れば、高さは$\left|\overrightarrow{\mathrm{RH}}\right|$となる。ここで、三角形$\mathrm{OPQ}$の面積は、

\[\frac{1}{2}pq\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}pq\]

であり、また、

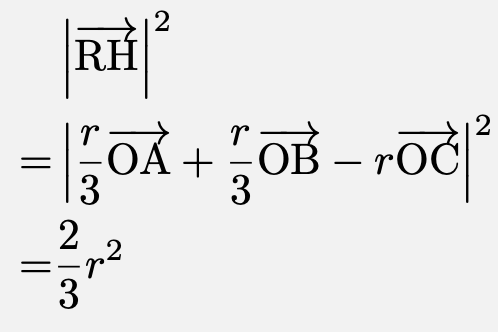
\begin{align*}&\left|\overrightarrow{\mathrm{RH}}\right|^2\\=&\left|\frac{r}{3}\overrightarrow{\mathrm{OA}}+\frac{r}{3}\overrightarrow{\mathrm{OB}}-r\overrightarrow{\mathrm{OC}}\right|^2\\=&\frac{2}{3}r^2\end{align*}

より、$\left|\overrightarrow{\mathrm{RH}}\right|=\frac{\sqrt{6}}{3}r$であるので、三角錐$\mathrm{OPQR}$の体積は、

\[\frac{1}{3}\cdot\frac{\sqrt{3}}{4}pq\cdot\frac{\sqrt{6}}{3}r=\frac{\sqrt{2}}{12}pqr\]

ここで、$p>0,\,q>0,\,r>0$より、相加平均相乗平均の大小関係から、

\[\frac{1}{p}+\frac{1}{q}+\frac{1}{r}\geqq 3\sqrt[3]{\frac{1}{pqr}}\]

が成り立つので、(1)と合わせて、

\[\sqrt[3]{pqr}\geqq \frac{3}{4}\Leftrightarrow pqr\geqq\left(\frac{3}{4}\right)^3\]

が言える。この等号が成立するのは、

\[p=q=r=\frac{3}{4}\]

のときで、これはたしかに$0<p<1,\,0<q<1,\,0<r<1$をみたす。したがって、求める最小値は、

\[\frac{\sqrt{2}}{12}\cdot\left(\frac{3}{4}\right)^3=\boldsymbol{\frac{9\sqrt{2}}{256}}\]

まとめ

・相加相乗平均の大小関係とは、0以上の実数に対して、相加平均が相乗平均以上になるという関係のこと

・相加相乗は最小値や最大値を求めるために用いることが多い

・相加相乗を使って最小値や最大値を求めるときには1.すべての数が0以上であるかたしかめる2.等号成立条件をチェックする3.定数でおさえる　の3つに注意する

数ⅠAⅡBカテゴリの最新記事