この記事を読むとわかること
・絶対値が付いたグラフの描き方2通り
・絶対値付きのグラフが関わる入試問題
絶対値が付いたグラフの描き方は?
絶対値が付いたグラフの描き方には主に2通りがあります。
絶対値が付いたグラフの描き方2通り!
1.絶対値の中身の正負で場合分けをする
2.$y=|f(x)|$の形なら、$y=f(x)$のグラフの$x$軸よりも下側を折り返す
それぞれについて説明していきます。
絶対値の中身の正負で場合分けするとき
まず、絶対値をそのまま処理することはできないので、絶対値は外して処理しなければなりません。
絶対値の定義は、
\[|x|=\left\{\begin{array}{l}-x(x<0のとき)\\x(x\geqq 0のとき)\end{array}\right.\]
であり、中身の正負によって外し方が変わるので、グラフを描くときも同じように中身の正負に気をつけなければなりません。
絶対値の中身で場合分けをしていけば、それぞれの場合でのグラフが描けるので、それを繋ぎ合わせれば描きたいグラフが出来上がります。
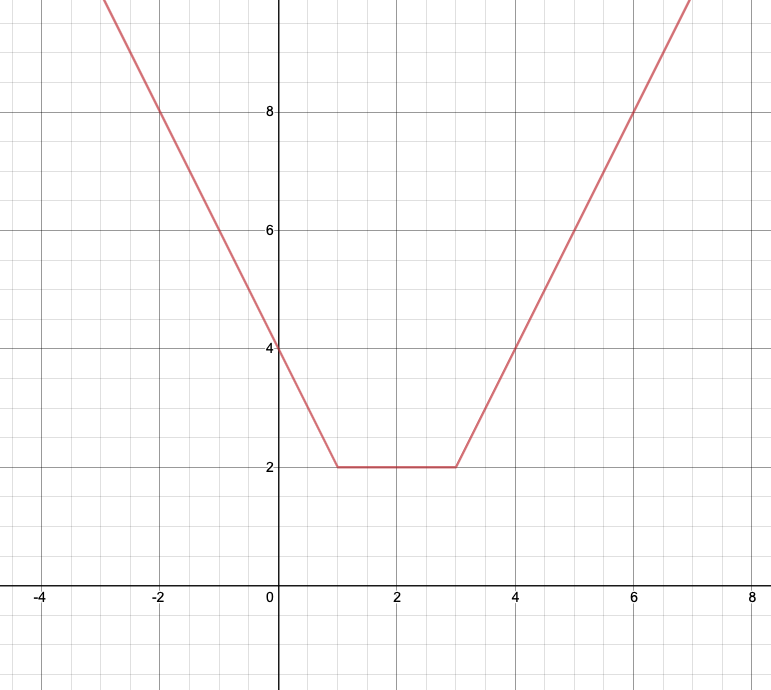
例えば、$y=|x-1|+|x-3|$のグラフを描くことを考えましょう。
$x-1$の正負が切り替わるのは$x=1$のときで、$x-3$の正負が切り替わるのは$x=3$のときなので、$x<1$のとき、$1\leqq x<3$のとき、$3\leqq x$の3つで場合分けをしてあげれば良さそうです。
$x<1$のとき、$|x-1|$の中身は負になって、$|x-3|$の中身も負になるので、絶対値を外すときにはマイナスが付いて、
\[y=-(x-1)-(x-3)=-2x+4\]
となります。
同様にして、$1\leqq x<3$のとき$y=2$、$3\leqq x$のとき$y=2x-4$となることがわかります。これをグラフにすると以下のようになります。
$y=|f(x)|$の形のとき
絶対値は中身の正負で場合分けして処理が基本ですが、描きたいのが$y=|f(x)|$の形のグラフのときは、$y=f(x)$のグラフの$x$軸の下側にある部分を$x$軸で折り返すことによって描くこともできます。
これは本質的には、$f(x)$の値が負のときがいつかを調べてそのときは$|f(x)|=-f(x)$とするということをやっているわけですが、この方法を知っていると、「グラフの$x$軸より下側にある部分を折り返して」とだけ記述で書けばいいので、記述の負担をぐっと減らすことができます。
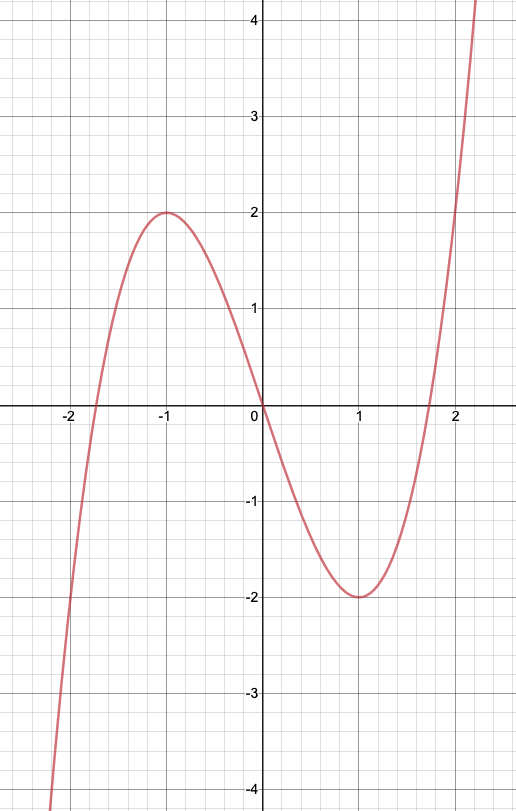
例えば、$y=|x^3-3x|$のグラフを描くことを考えましょう。
まずは、$y=x^3-3x$のグラフを描きます。これは微分をすれば簡単に描けますね。
\[y’=3x^2-3=3(x-1)(x+1)\]
より、増減表は以下のようになります。
\[\begin{array}{|c||c|c|c|c|c|} \hline x&\cdots&-1&\cdots&1&\cdots\\\hline y’&+&0&-&0&+\\\hline
y&\nearrow&2&\searrow&-2&\nearrow\\\hline\end{array}\]
さらに、$x$軸との交点は、
\[x^3-3x=x(x-\sqrt{3})(x+\sqrt{3})\]
より、$(-\sqrt{3},\,0),\,(\sqrt{3},\,0)$の2点であるので、以下のようになります。
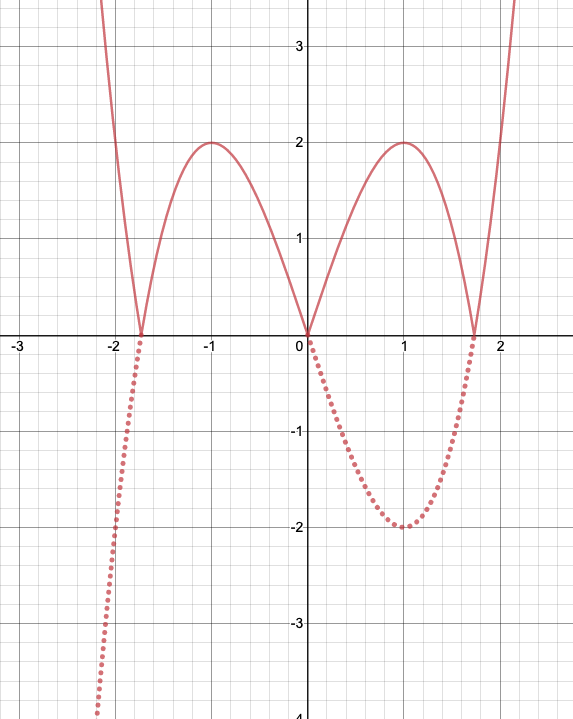
このグラフのうち、$x$軸よりも下側にある部分を$x$軸で折り返すと$y=|x^3-3x|$のグラフが出来上がります。
絶対値付きのグラフが関わる入試問題3選
絶対値付きのグラフの描き方がわかったら、演習問題を解きましょう!
問題1

解答・解説
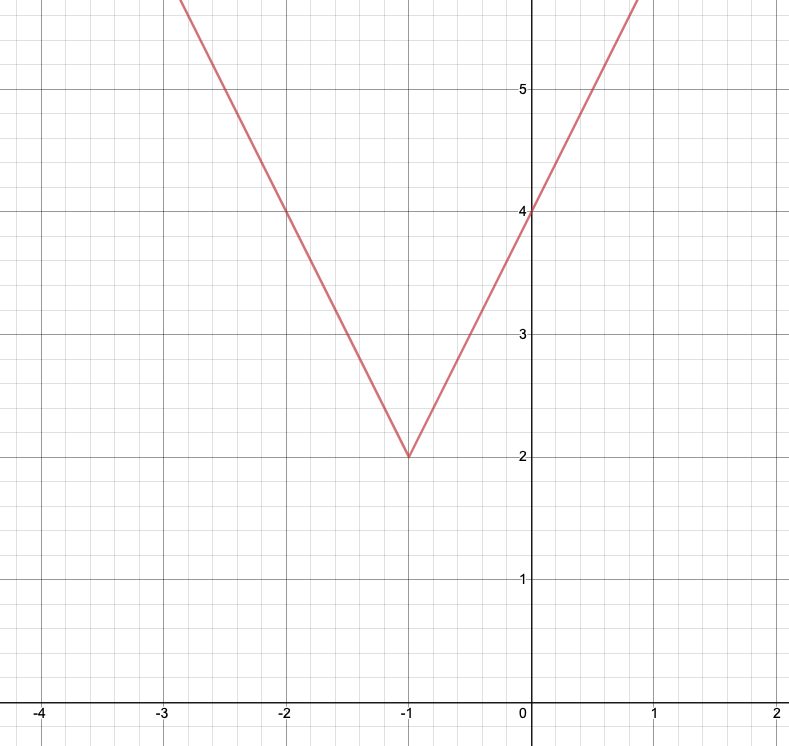
$y=|2x+2|+2$という絶対値付きのグラフを描くことがポイントとなります。
絶対値の中身で場合分けをするという方針であれば、$2x+2$の正負が切り替わるのは$x=-1$のときなので、$x<-1$のときと$-1\leqq x$のときで場合分けをしてあげればグラフを描くことができますね。
$x<-1$のときは$2x+2$は負なので絶対値を外すときにはマイナスが付いて、
\[y=-(2x+2)+2=-2x\]
となります。
同様にして、$-1\leqq x$のときは、
\[y=(2x+2)+2=2x+4\]
となるので、グラフは以下のようになります。
これと$y=6$で囲まれた領域は下図のようになります。
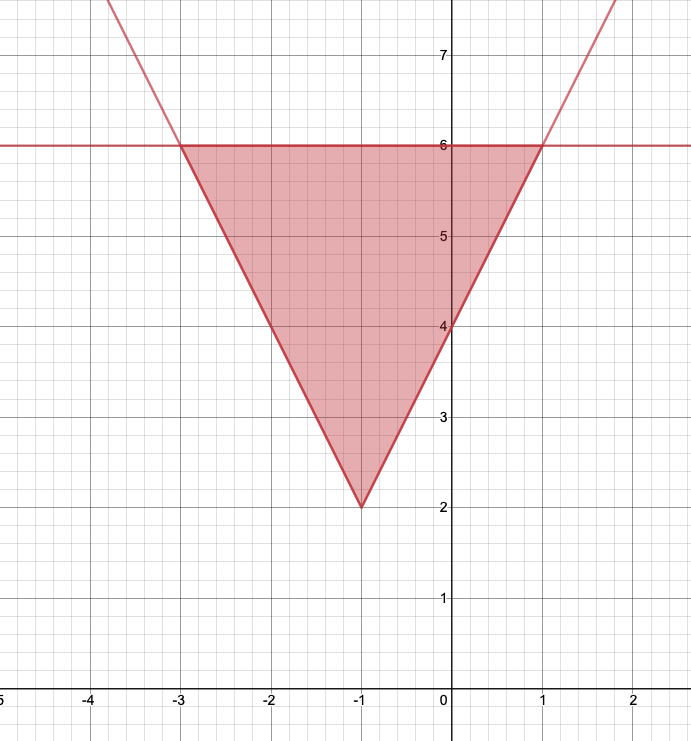
これは、底辺の長さが$4$で、高さが$4$の三角形と見ることができるので、求める面積は、
\[\frac{1}{2} \cdot 4\cdot 4=\boldsymbol{8}\]
となります。
これは公務員試験の数的処理の過去問です。公務員試験で出題される数学の対策については以下の記事が詳しいです。
問題2

解答・解説
問われていることは複雑に見えますが、結局のところ$|x^2+x+a|$の$-1\leqq x\leqq 1$における最大値を求めよと言われているに過ぎません。
2次関数の最大値について調べるのでグラフを用いて考えていきましょう。$y=|x^2+x+a|$は$y=|f(x)|$の形をしているので、$y=x^2+x+a$のグラフを描いてから$x$軸の下側にある部分を折り返してあげればOKです。
グラフの形を把握するために平方完成をすると、
\[x^2+x+a=\left(x+\frac{1}{2}\right)^2+a-\frac{1}{4}\]
となるので、$a\geq\frac{1}{4}$のときは、常に$x^2+x+a\geqq 0$となり、グラフの形は下のようになりますね。
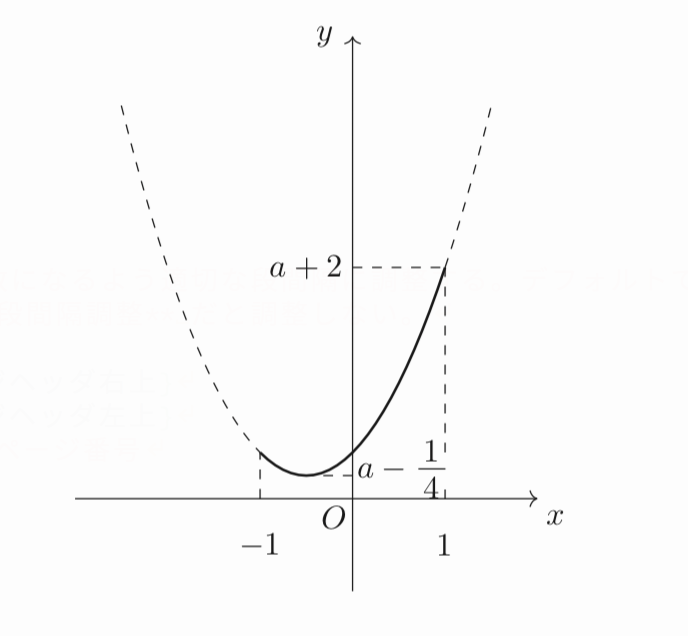
このとき、最大値は$x=1$のときに取り、その最大値は$a+2$ですね。よって、$k=a+2$となります。
次に、$a<\frac{1}{4}$の場合を考えましょう。絶対値が付いているので、グラフの形状は下図のようになりますね。
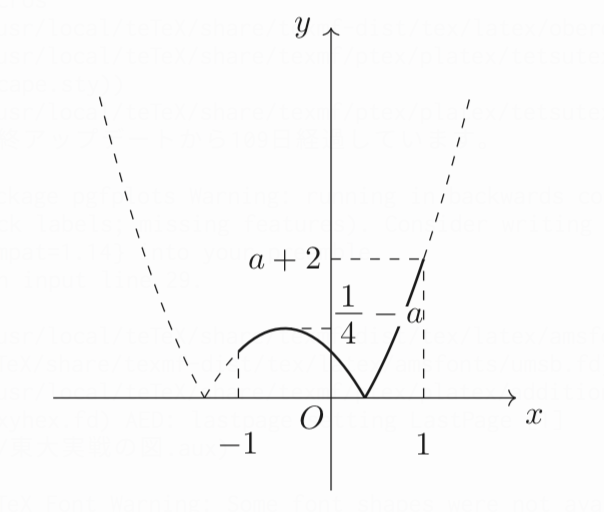
さて、$\boldsymbol{x=1}$のときに最大値を取るという状況が崩れるのはいつでしょうか。それは、頂点の$y$座標が$a+2$以上になるときですね。つまり、
\[\frac{1}{4}-a\geqq a+2\Leftrightarrow a\leqq -\frac{7}{8}\]
のときとなります。これよりも$ a $が小さくなっても、頂点で最大値を取る状況は変わりませんから、結局場合分けは2つで済むとわかります。
頂点の$y$座標は、$\frac{1}{4}-a$なので、$k=\frac{1}{4}-a$となります。したがって、求める$k$の最小値は、
\[\left\{\begin{array}{l}\boldsymbol{a+2(a>-\frac{7}{8}のとき)}\\\boldsymbol{\frac{1}{4}-a(a\leqq -\frac{7}{8}のとき)}\end{array}\right.\]
となります。
問題3

解答・解説
解の配置の問題です。方程式の実数解の個数を$y=x|x-3|$と$y=ax+1$の共有点の個数と捉えます。$y=x|x-3|$のグラフを描くところで場合分けをすることになりますね。
解の配置の解き方を忘れてしまった人にははこの記事がおすすめです。
共有点の個数が変わるのは、接するときと端点を通るときなので、そのときの$a$の値を求めることが大切になります。
以下、解答例です。
\[\begin{align*}y=&x|x-3|\\=&\left\{\begin{array}{l}x(x-3)(x\geqq 3のとき)\\-x(x-3)(x< 3のとき)\end{array}\right.\end{align*}\]
である。
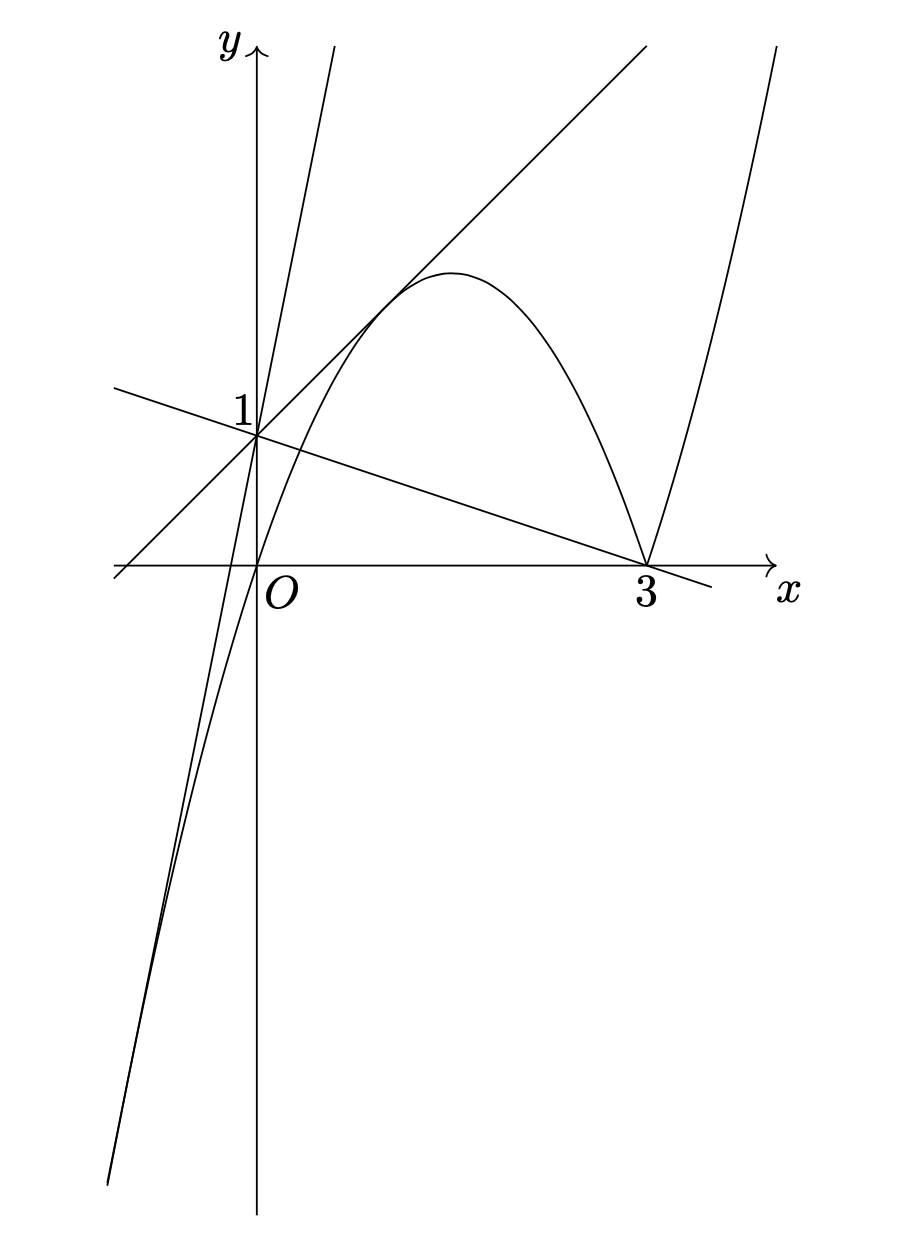
$y=ax+1$が$y=x|x-3|$と接する時、上のグラフより、$y=-x(x-3)$と接する時を考えればよい。このとき、
\[-x(x-3)=ax+1\Leftrightarrow x^2+(a-3)x+1=0\]
が重解を持つので、この判別式を$D$とすると、
\[\begin{align*}&D=0\\\Leftrightarrow &(a-3)^2-4=0\\\Leftrightarrow &a^2-6a+5=0\\\Leftrightarrow &a=1,\,5\end{align*}\]
このときの重解はそれぞれ、
\[x=-\frac{a-3}{2}=\left\{\begin{array}{l}1(a=1のとき)\\-1(a=5のとき)\end{array}\right.\]
で、どちらも$x<3$を満たすので、たしかに$y=ax+1$と$y=x|x-3|$は接している。
また、$y=ax+1$が点$(3,\,0)$を通るとき、
\[0=3a+1\Leftrightarrow a=-\frac{1}{3}\]
与えられた方程式の実数解は、$y=ax+1$と$y=x|x-3|$の共有点の$x$座標であり、相異なる実数解の個数は相異なる共有点の個数に等しいので、上のグラフより、相異なる実数解の個数は、
\[\left\{\begin{array}{l}\boldsymbol{a<-\frac{1}{3}のとき1個}\\\boldsymbol{a=-\frac{1}{3}のとき2個}\\\boldsymbol{-\frac{1}{3}<a<1のとき3個}\\\boldsymbol{a=1のとき2個}\\\boldsymbol{1<a<5のとき1個}\\\boldsymbol{a=5のとき2個\\a>5のとき3個}\end{array}\right.\]
接する時の$a$の値を求めるときには、接している点の$x$座標が$x>3$の範囲内に入っているのかをチェックする必要があることに気をつけましょう。
また、重解の値は軸の位置と同じであるので、
\[x^2+(a-3)x+1=\left(x+\frac{a-3}{2}\right)^2+1-\left(\frac{a-3}{2}\right)^2\]
より、
\[x=-\frac{a-3}{2}\]
として求めています。
まとめ
・絶対値がついたグラフは基本的には絶対値の中身で場合分け
・$y=|f(x)|$の形 の場合は、$y=f(x)$のグラフを描いてから$x$軸より下側にある部分を折り返せばOK






