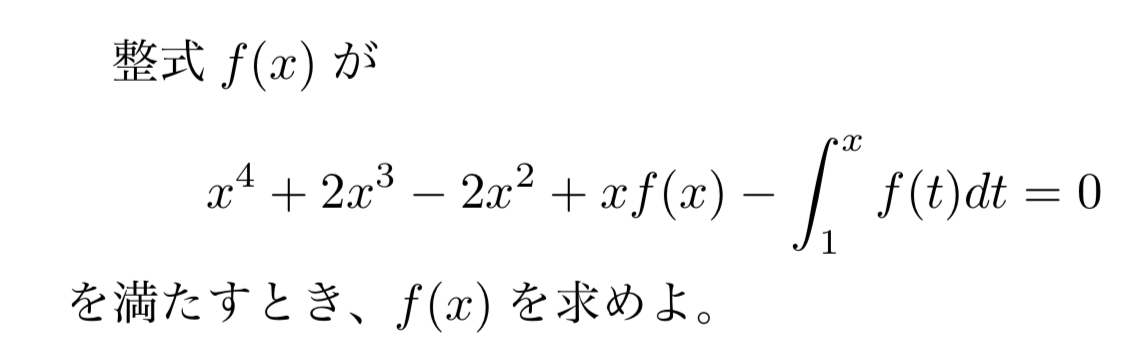この記事を読むとわかること
・微分積分学の基本定理とはなにか
・微分積分学の基本定理が高校数学で役立つのはいつか
・微分積分学の基本定理が関わる入試問題
微分積分学の基本定理とは?
微分積分学の基本定理とは積分の微分が元に戻ること
微分積分学の基本定理とは、ある関数を積分して微分すると元の関数になるという定理です。すなわち、$a$を定数として、
\[\left(\int_{a}^{x}f(t)dt\right)’=f(x)\]
となるという事実が微分積分学の基本定理です。
積分区間が複雑な関数なら合成関数の微分を使う
積分の微分だからといっていつも$f(x)$に戻るわけではありません。例えば、積分区間が$a$から$2x$であれば、
\[\left(\int_{a}^{2x}f(t)dt\right)’=2f(2x)\]
となります。これは合成関数の微分になるので$2x$の微分である2をかけてあげていると見ればすぐわかると思います。
一般化すると、$g(x)$から$h(x)$までの積分の微分であれば、合成関数の微分公式を用いて、
\[\left(\int_{g(x)}^{h(x)}f(t)dt\right)’=h’(x)f(h(x))-g’(x)f(g(x))\]
となります。このように、積分区間の端が複雑な関数になっていた場合は微分積分学の基本定理と合成関数微分公式を用いて微分ができます。
微分積分学の基本定理が高校数学で役立つのはいつ?
微分積分学の基本定理というかなり当たり前にも見える定理が高校数学において役立つ場面はいつなんでしょうか?
主にこの2つの場面だと思います。
微分積分学の基本定理を使うべきとき2つ!
1.積分漸化式によって定義された関数の微分
2.積分方程式を解くとき
それぞれについて見ていきましょう。
積分漸化式によって定義された関数の微分
関数が積分漸化式によって定義されているときには、微分積分学の基本定理が有効なときがあります。例えば、
\[f_{n+1}(x)=1+\int_{0}^{x}f_n(t)dt\]
という漸化式がある場合、$f_{n+1}'(x)$は微分積分学の基本定理から$f_n(x)$に等しくなることがわかります。
積分方程式を解く時
$f(x)$の積分の形が含まれている$f(x)$を決定するための方程式のことを積分方程式と呼びます。積分方程式には大きく分けて積分区間が定数だけのパターン、積分区間に$x$が含まれているパターンの2パターンがあります。
前者では、定積分の値はただの定数になるので、それを文字で置いてあげればOKです。後者では、微積分学の基本定理を用いて両辺を微分することで$f(x)$の条件を得ることになります。
微分積分学の基本定理が関わる入試問題3選
微分積分学の基本定理を理解したらあとは演習を積みましょう!
問題1
解答・解説
積分区間に$x$が含まれているパターンの積分漸化式を解くことになるので、
1.$x$に積分区間のもう一方の端の値を代入して条件を得る
2.微分積分学の基本定理の基本定理を用いて両辺を$x$で微分する
という手順を踏むことになります。1の作業がなぜ必要かというと、微分をすると、定数の部分の条件が失われてしまうからです。微分したあとの式からは、元の式の定数項がなんだったかという情報は得られないですよね。そのため、不定積分のときには積分定数$C$などを付け加える必要があるんでした。
以下、解答例です。
与えられた方程式に$x=1$を代入して、
\[1+2-2+f(1)-0=0\Leftrightarrow f(1)=-1\]
与えられた方程式の両辺を$x$で微分して、
\[4x^3+6x^2-4x+f(x)+xf'(x)-f(x)=0\Leftrightarrow xf'(x)=-4x^3-6x^2+4x\]
これが常に成り立つので、
\[f'(x)=-4x^2-6x+4\]
となる。よって、
\[f(x)=\int f'(x)dx=-\frac{4}{3}x^3-3x^2+4x+C(Cは定数)\]
となる。$f(1)=-1$から、$C=\frac{1}{3}$だと分かるので、
\[\boldsymbol{f(x)=-\frac{4}{3}x^3-3x^2+4x+\frac{1}{3}}\]
$x=1$を代入した時は積分区間が$1$から$1$となるので、積分値が$0$になることを用いていることに注意しましょう。
また、$x$は$0$になりうる数であるので、
\[xf'(x)=-4x^3-6x^2+4x\]
において、$x$で割るという操作はせずに、これが恒等的に成り立つには、
\[f'(x)=-4x^2-6x+4\]
しかないという記述をするように気をつけましょう。
問題2

解答・解説
2つの関数が絡んだ積分方程式です。このときも、積分区間がどうなっているかに着目するのは変わりません。積分区間に$x$が含まれているので、
1.$x$に積分区間のもう一方の端の値を代入して条件を得る
2.微分積分学の基本定理の基本定理を用いて両辺を$x$で微分する
の2つの作業をやるだけです。また、今回$g(x)$が3次関数であるという条件も忘れないようにしましょう。
以下、解答例です。
(1) 与えられた方程式に$x=0$を代入して、
\[g(0)=0\]
与えられた方程式の両辺を$x$で微分して、
\[f(x)=f(x)+xf'(x)+g'(x)\Leftrightarrow g'(x)=-xf'(x)\]
これに$x=0$を代入して、
\[g'(0)=0\]
また、$g(x)$は$x=\frac{1}{2}$で極値を持つから
\[g’\left(\frac{1}{2}\right)=0\]
が必要。ここで、$g(x)$は3次関数より、$g'(x)$は2次関数であるので、$a$を定数として、
\[g'(x)=ax\left(x-\frac{1}{2}\right)\]
と表すことができる。これより、
\[g(x)=\int g'(x)=\frac{a}{3}x^3-\frac{a}{4}x^2+C(Cは定数)\]
となる。$g(0)=0$および$g(1)=\frac{1}{3}$から、
\[C=0,\,a=4\]
と分かるので、
\[\boldsymbol{g(x)=\frac{4}{3}x^3-x^2}\]
このときたしかに$g(x)$は$x=\frac{1}{2}$で極値を持つので十分。
(2) $g'(x)=-xf'(x)$および(1)より、
\[-xf'(x)=4x^2-2x\]
が常に成り立つから、
\[f'(x)=-4x+2\]
である。よって、
\[f(x)=\int f'(x)=-2x^2+2x+D(Dは定数)\]
となる。$f(1)=5$より$D=5$が分かるので、
\[\boldsymbol{f(x)=-2x^2+2x+5}\]
問題3

解答・解説
積分漸化式によって定義された関数を求める問題です。(1)は、結果を予想して数学的帰納法によって証明することで求まります。
(2)では$f_n(x)$の微分を計算することになりますが、このとき、普通に微分を計算してもよいのですが、与えられた漸化式を利用して、微積分学の基本定理から、
\[f_n'(x)=f_{n-1}(x)\]
と計算してもよいでしょう。詳しい解説は以下の記事にあります。
まとめ
・微分積分学の基本定理とは「積分の微分が元に戻る」という定理
・高校数学において微分積分学の定理が役立つのは
1.積分漸化式で定義された関数を微分するとき
2.積分区間に$x$が含まれているタイプの積分方程式を解く時
の2つ