この記事を読むとわかること
・媒介変数表示されたグラフの回転体の体積の求め方
・回転体の体積を求める入試問題
媒介変数表示されたグラフの回転体の体積の求め方は?
パラメータで微分して概形を描く
まずは、積分区間などを知るために、媒介変数表示されたグラフがどのような形なのか把握する必要があります。そのためには、パラメータで微分して、増減表を描いて、グラフの概形を描きます。
断面の面積を積分した式を立てる
次に、回転体を回転軸に対して垂直に切ったときの断面積を、回転軸方向に積分する式を立てます。このとき、断面は円になることがほとんどなので、$x$軸を回転軸として回転させた場合には、$\pi y^2$を積分する式を立てればよいことになります。
積分区間は先ほどグラフの概形を描いたことによって分かるはずです。
線分を回転させたときにでてくるのが円でない可能性もあることにも注意しましょう。例えば、下図のようなグラフの紫色の直線で切った部分グラフを回転させたときには、円の中から円をくり抜いた形が断面になります。よって、この場合は、赤色の部分を$y^+$、緑色の部分を$y^-$とおけば、$\pi \{(y^+)^2-(y^-)^2\}$を$x$軸方向に積分すればいいことになります。
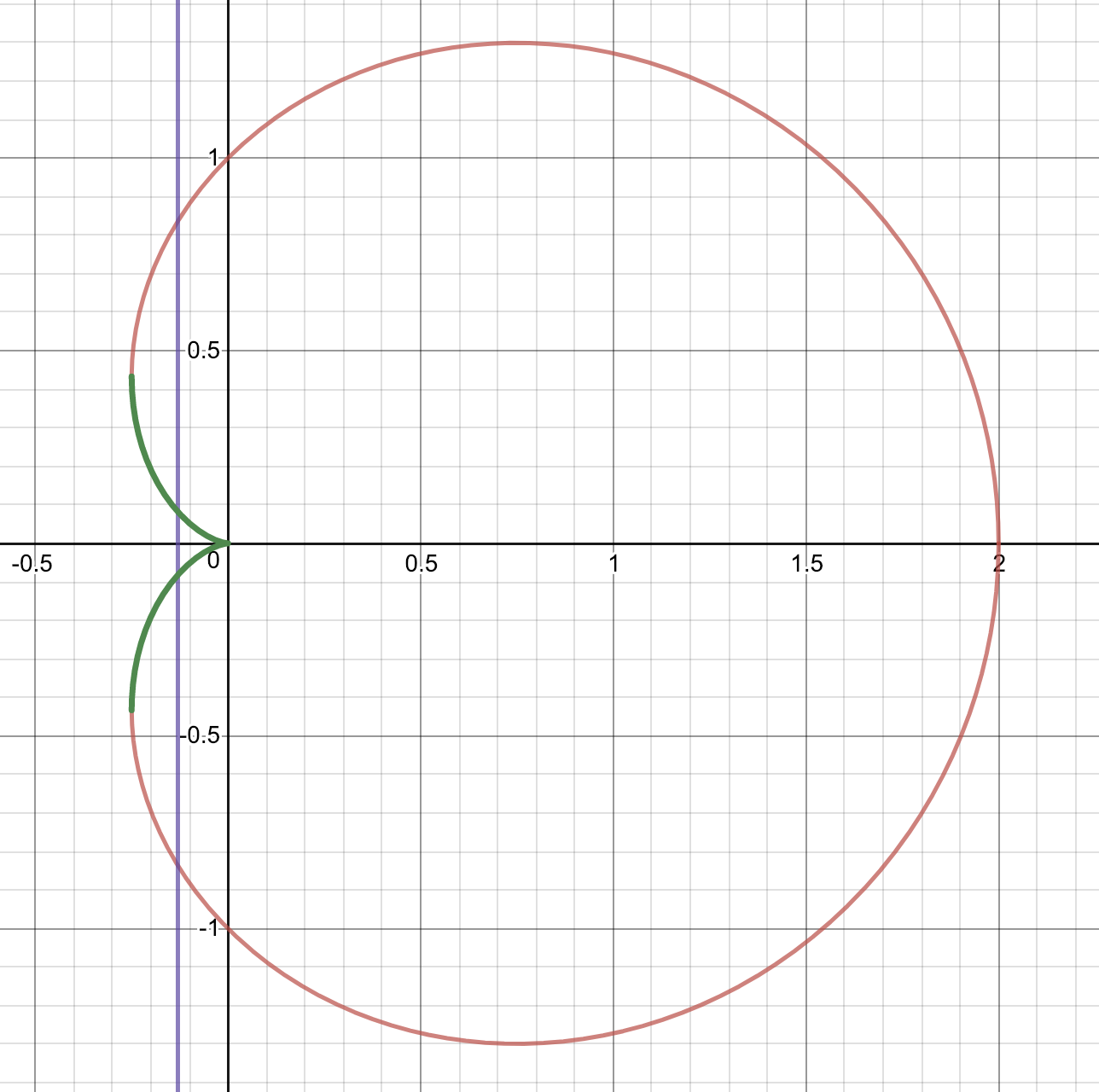
パラメータで置換積分する
最後に、パラメータで置換積分をします。このとき、1つ前の段階では場合分けをして立式していたとしても、パラメータで置換したあとには積分区間が必ず繋がることを覚えておきましょう。
上図の例で言えば、$x\leqq 0$の部分と$x\geqq 0$の部分で場合分けをして、積分の和としてをしなければなりませんが、パラメータで置換したあとは1つの積分に必ずまとめられるということです。
媒介変数表示された回転体の体積を求める入試問題
やり方がある程度理解できたら、実際の入試問題を通して理解を深めましょう!今回はカージオイドとアステロイドという有名な媒介変数表示された曲線を取り上げています。
例題1(カージオイド)
問題
\[\left\{\begin{array}{l}x=\cos t(1+\cos t)\\y=\sin t(1+\cos t)\end{array}\right.(0\leqq t\leqq 2\pi)\]
で表される曲線に囲まれた部分を$x$軸の周りに1回転させたときに通過する部分の体積を求めよ。
解答
\[\cos (2\pi -t)\{1+\cos(2\pi -t)\}=\cos t(1+\cos t)\]
\[\sin(2\pi -t)\{1+\cos(2\pi -t)\}=-\sin t(1+\cos t)\]
であることから、題意の曲線は$x$軸に関して対称である。よって、$0\leqq t\leqq \pi$の範囲の曲線と$x$軸で囲まれた図形を$x$軸を中心に回転させてできる体積を求めればよい。
\[\begin{align*}&\left\{\begin{array}{l}\frac{dx}{dt}=-\sin t(1+2\cos t)\\\frac{dy}{dt}=\cos t+\cos 2t\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}\frac{dx}{dt}=-\sin t(1+2\cos t)\\\frac{dy}{dt}=2\cos \frac{3}{2}t\cos \frac{1}{2}t\end{array}\right.\end{align*}\]
であるから、$0\leqq t\leqq\pi$の範囲における増減表は以下のようになる。
よって、$0\leqq t\leqq\pi$の範囲におけるグラフと$x$軸に囲まれた図形は以下のようになる。
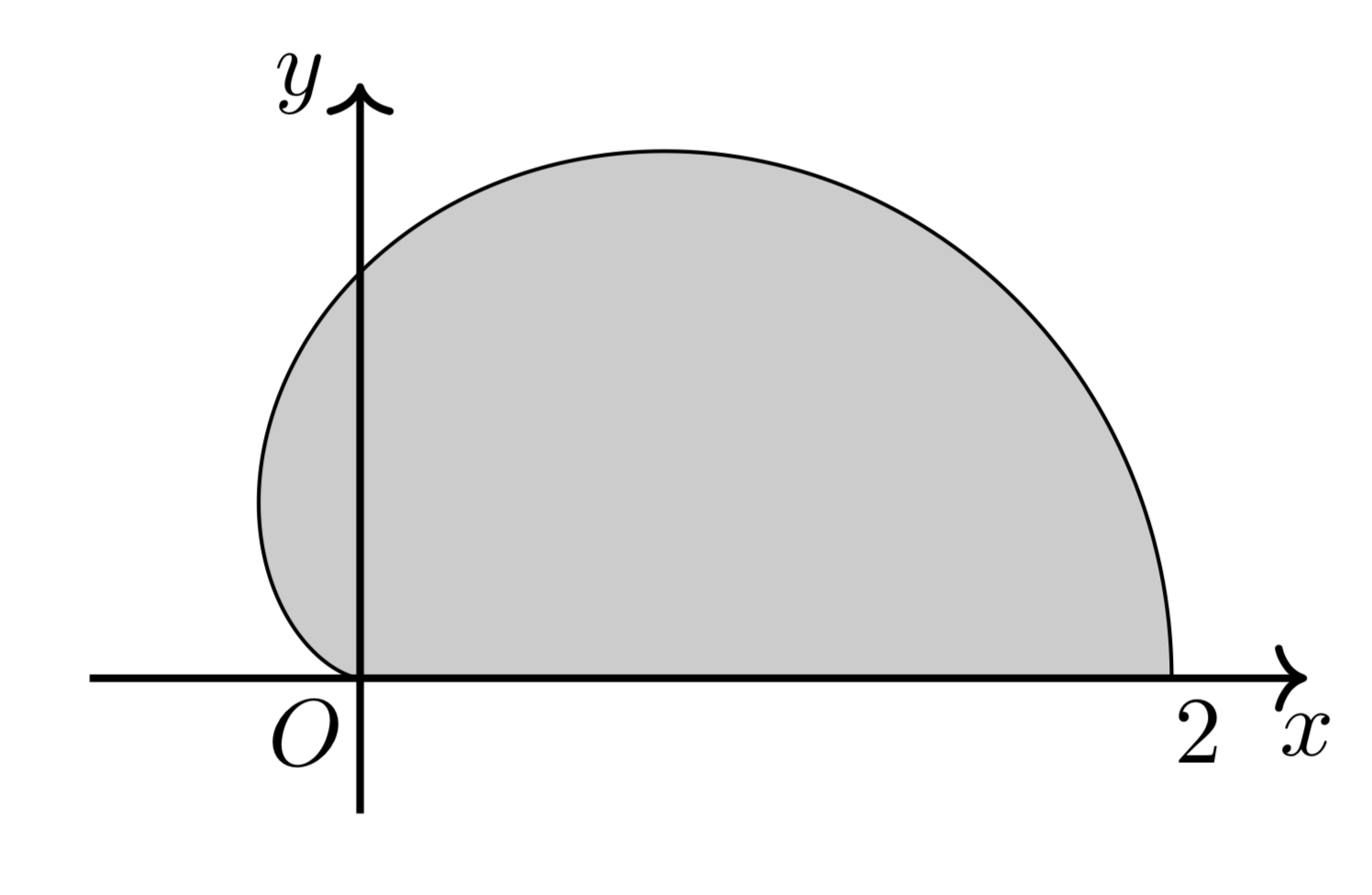
これと、直線$x=p(-\frac{1}{4}\leqq p\leqq 2)$の共有部分を$x$軸の周りに回転させてできる図形の面積を、$x$軸方向に積分すれば題意の体積は求まる。
よって、$0\leqq t\leqq \frac{2}{3}\pi$の部分の$y$座標を$y^+$、$\frac{2}{3}\pi\leqq t\leqq\pi $の部分の$y$座標を$y^-$とすれば、求める体積は、
ここで、$s=\cos x$と置換して、
\[\begin{align*}&\pi\int_{1}^{-1}(s^2-1)(1+s)^2(1+2s)ds\\=&\pi\int_{1}^{-1}(2s^5+5s^4+2s^3-4s^2-4s-1)ds\\=&\pi\left[\frac{1}{3}s^6+s^5+\frac{1}{2}s^3-\frac{4}{3}s^3-2s^2-s\right]_{1}^{-1}\\=&\boldsymbol{\frac{8}{3}\pi}\end{align*}\]
積分の立式の段階までは簡単ですが、そのあとの積分が少々難しいかと思います。
$\sin^3 t$のうちの$\sin t$だけを残して、他はすべて$\cos t$の関数として表せるので、$\cos t$の微分が$-\sin t$になることに注目して、置換積分を施してあげると多項式の積分に帰着できます。
三角関数の偶数乗は、倍角公式を利用して次数下げを行っていくのが定石であり、奇数次の場合はこのように綺麗に積分できる場合があるので覚えておきたいところです。
ちなみに、回転体を3Dで表すと以下の図のようになります。

例題2(アステロイド)
問題
\[\left\{\begin{array}{l}x=\cos^3 t\\y=\sin^3 t\end{array}\right.(0\leqq t\leqq 2\pi)\]
で表される曲線で囲まれた部分を$x$軸のまわりに1回転させたときに通過する部分の体積を求めよ。
解答
\[\cos^3 (2\pi-t)=\cos^3 t\]
\[\sin^3 (2\pi-t)=-\sin^3 t\]
より、題意の曲線は$y$軸に関して対称である。また、
\[\cos^3 (\pi-t)=-\cos^3 t\]
\[\sin^3 (\pi-t)=\sin^3 t\]
より、題意の曲線は$x$軸に関しても対称である。
よって、$0\leqq t\leqq \frac{\pi}{2}$の範囲の曲線と$x$軸、$y$軸で囲まれた図形を$x$軸を中心に回転させてできる体積の2倍を求めればよい。
ここで、
\[\left\{\begin{array}{l}\frac{dx}{dt}=-3\cos^2 t\sin t\\\frac{dy}{dt}=3\sin^2 t\cos t\end{array}\right.\]
であるから、$0\leqq t\leqq\frac{\pi}{2}$の範囲における増減表は以下のようになる。
\[\begin{array}{|c||c|c|c|} \hline t&0&\cdots&\frac{\pi}{2}\\\hline\frac{dx}{dt}&0&-&0\\\hline \frac{dy}{dt}&0&+&0\\\hline
(x,\,y)&(1,\,0)&\nwarrow&(0,\,1)\\\hline\end{array}\]
よって、$0\leqq t\leqq \frac{\pi}{2}$の範囲の曲線と$x$軸、$y$軸で囲まれた図形は以下のようになる。
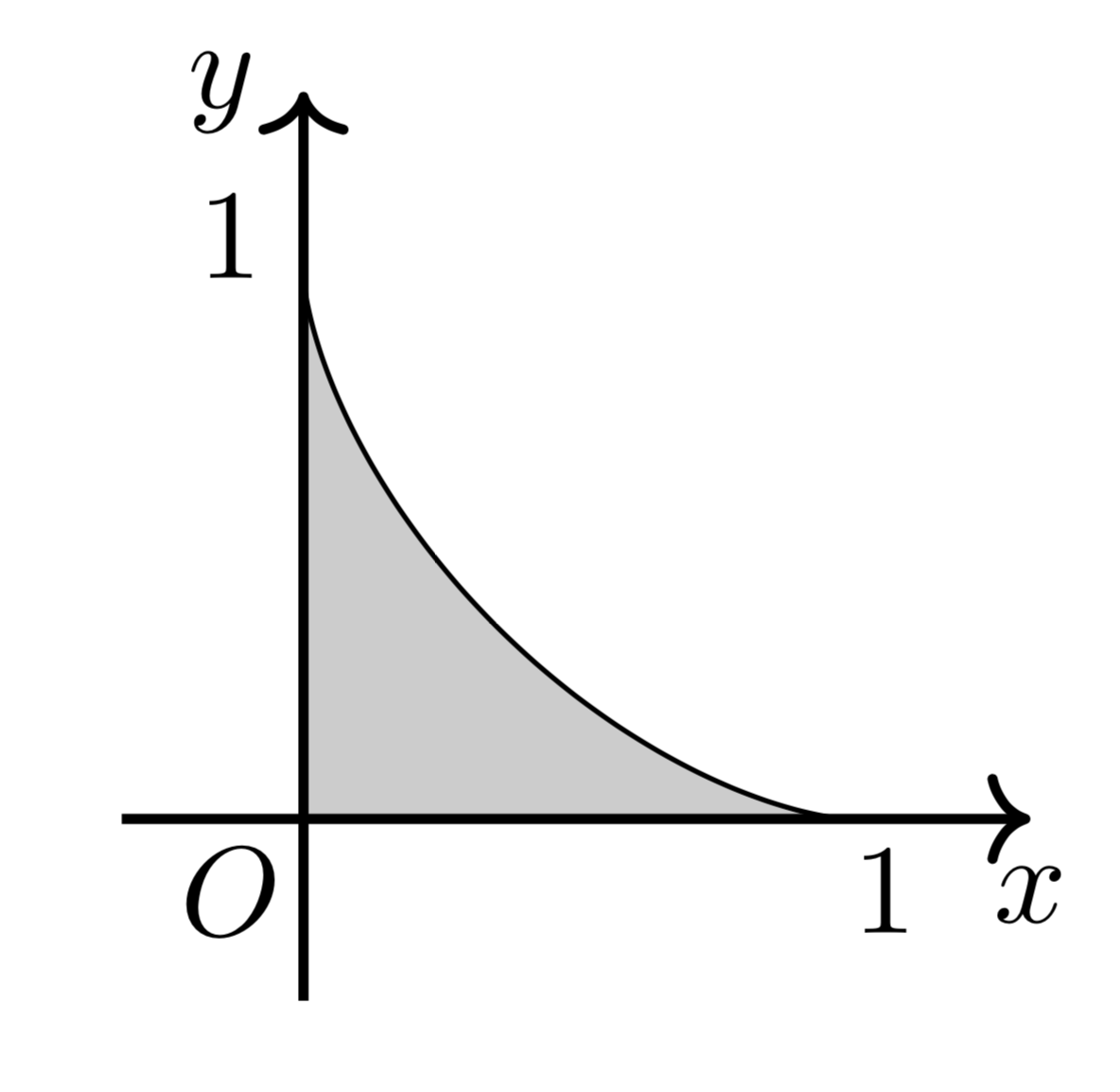
これと、直線$x=p(0\leqq p\leqq 1)$の共有部分を$x$軸の周りに回転させてできる円の面積を、$x$軸方向に積分すれば題意の体積の半分が求まる。
求める体積の半分は、
\[\begin{align*}&\int_{0}^{1}\pi y^2dx\\=&\pi\int_{\frac{\pi}{2}}^{0}(\sin^3 t)^2(-3\sin t\cos^2t)dt\\=&3\pi\int^{\frac{\pi}{2}}_{0}\sin^7 t\cos^2tdt\\=&3\pi\int^{\frac{\pi}{2}}_{0}\sin t(1-\cos^2 t)^3\cos^2t)dt\end{align*}\]
ここで、$s=\cos x$と置換して、
\[\begin{align*}&3\pi\int^{0}_{1}s^2(s^2-1)^3ds\\=&3\pi\int^{0}_{1}s^8-3s^6+3s^4-s^2ds\\=&3\pi\left[\frac{1}{9}s^9-\frac{3}{7}s^7+\frac{3}{5}s^5-\frac{1}{3}s^3\right]_{1}^{0}\\=&\frac{16}{105}\pi\end{align*}\]
求める体積はこの2倍で、
\[\boldsymbol{\frac{32}{105}\pi}\]
アステロイドの場合は、断面がすべて円になるので、積分の立式で場合分けをする必要がありません。置換積分したあとは、先ほどと同様にして、$\sin t$を1つだけ残して、他を$\cos t$だけの関数で表せば、置換積分をすると多項式の積分に帰着できます。
ちなみに、回転体の立体図は以下のようになります。
まとめ
・媒介変数表示されたグラフの回転体の体積を求めるときは、
1.パラメータで微分して増減表を描いてグラフの概形を把握する
2.断面積を積分する式を立てる
3.パラメータで置換積分する
の3ステップでできる
・積分の立式をするときは、断面が円でない場合に気をつける
・置換積分したあとは積分区間が必ず繋がる