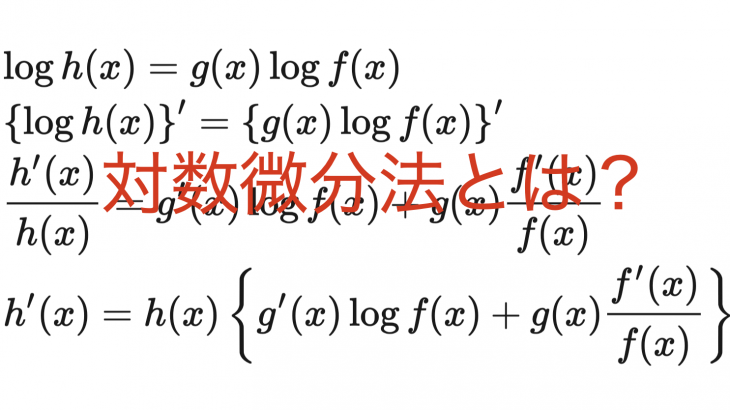この記事を読むとわかること
・対数微分法とはなにか
・対数微分法を使う時はいつか
・対数微分法で対数を取らない裏技
・対数微分法に関する入試問題
対数微分法とは
対数微分法とは$f(x)^{g(x)}$の形の関数を微分する方法
対数微分法とは、$h(x)=f(x)^{g(x)}$の形の関数を、
\[\begin{align*}&\log{h(x)}=g(x)\log{f(x)}\\&\left\{\log{h(x)}\right\}’=\left\{g(x)\log{f(x)}\right\}’\\&\frac{h'(x)}{h(x)}=g'(x)\log{f(x)}+g(x)\frac{f'(x)}{f(x)}\\&h'(x)=h(x)\left\{g'(x)\log{f(x)}+g(x)\frac{f'(x)}{f(x)}\right\}\end{align*}\]
とすることによって上手く微分する手法のことです。
対数微分法を使うときに底は$e$を選ぶと楽
対数微分法を用いるときに底として何を選べばよいか迷う人がいるかと思いますが、必ず$e$を選びましょう。なぜなら、それが最も計算が楽になるからです。
対数微分法では、$\log \{f(x)\}$の微分をすることになるので、対数の微分公式を用いる必要があります。このときに底が$e$でないと、$\log a$で割るなどの面倒な操作が出てくることになりますよね。よって、底としては$e$を選んでおくのがよいと言えます。
底が$e$である対数のことを自然対数と呼び、また、高校数学においては底が省略された対数が自然対数を表すことも併せて思い出しておきましょう。
対数微分法を使う時はいつ?
対数微分法を使うのは以下の3つのときです。
対数微分法を使うとき3つ
1.指数関数の微分公式の証明のとき
2.$f(x)$も$g(x)$も定数でない$f(x)^{g(x)}$の形の関数を微分するとき
3.積や累乗がたくさん出てくる式を微分するとき
それぞれについて詳しく見ていきましょう。
指数関数の微分公式の証明のとき
$f(x)^{g(x)}$の形であっても、$f(x)$が定数であれば、指数関数の微分公式や合成関数の微分公式によって微分することができますが、そもそも指数関数の微分公式を証明しなければならないときには対数微分法を用いることになります。
$y=a^x(a>0,\,a\ne 1)$において、$y’$を求めてみましょう。
$y=a^x(a>0,\,a\ne 1)$は常に正であるから、両辺に自然対数を取ることができて、
\[\log y=x\log a\]
両辺を$x$で微分すると、
\[\frac{y’}{y}=\log a\Leftrightarrow \boldsymbol{y’=a^x\log a}\]
となり、指数関数の微分公式を証明することができました。
東大をはじめとする難関大学の入試では、当たり前のように使っている定理の証明を求められることがしばしばあるので、このあたりも押さえておきたいですね。
$f(x)$も$g(x)$も定数でない$f(x)^{g(x)}$の形の関数を微分するとき
$f(x)$も$g(x)$も定数でない$f(x)^{g(x)}$の形の関数を微分するというのが、対数微分法の最も大事な用途です。例えば、$x^x$などは、習ったことのある微分公式で微分ができませんよね。
そこで、対数微分法を用いることによって、微分してみましょう。
$f(x)=x^x(x>0)$とおくと、これは常に正であるから、両辺に自然対数を取ることができて、
\[\log f(x)=x\log x\]
両辺$x$で微分すると、
\[\frac{f'(x)}{f(x)}=\log x+1\Leftrightarrow f'(x)=\boldsymbol{x^x\left(\log x+1\right)}\]
このようにして微分ができました!
正のものにしか対数を取ることはできないので、定義域が$x>0$になっていること、そして、記述で「常に正であるから」と述べていることにも注意しましょう。
積や累乗がたくさん出てくる式を微分するとき
たくさんの因数の積や累乗で構成された式は、対数微分法を用いると計算が簡単になります。以下の例題を考えてみましょう。
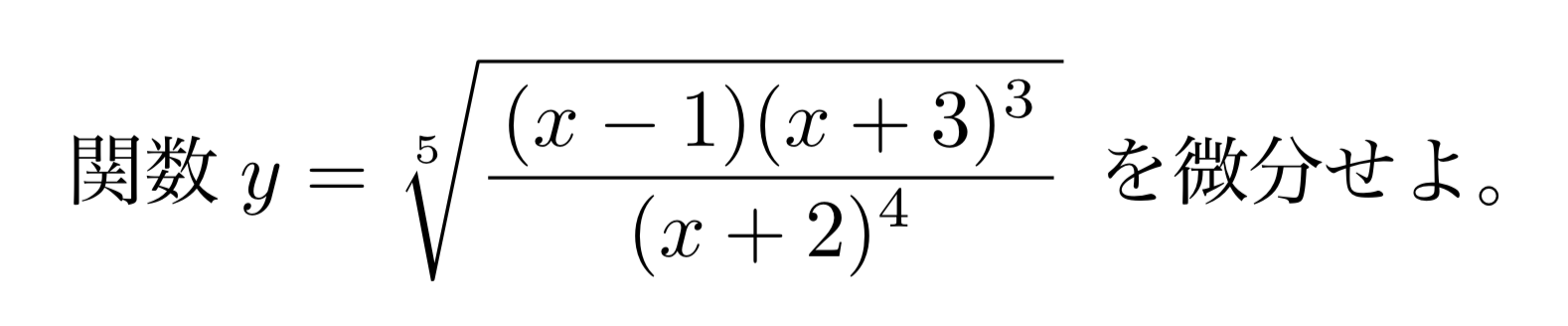
これを普通に微分しようとすると、合成関数の微分公式や積の微分公式、商の微分公式などを色々使ったかなり複雑な計算をすることになります。
対数を取ると積を和の形に変形できて、また、累乗はただの掛け算になるので、こういった積や累乗がたくさん出てくる関数は対数を取ってから微分することで実は簡単に計算ができるんです。これが、まさに対数微分法なわけですね。
\[y=\sqrt[5]{\frac{(x-1)(x+3)^3}{(x+2)^4}}\]
の両辺の絶対値を取ってから自然対数を取ると、
\[\log |y|=\frac{1}{5}(\log|x-1|+3\log|x+3|-4\log |x+2|)\]
となる。この両辺を$x$で微分して、
\[\frac{y’}{y}=\frac{1}{5}\left(\frac{1}{x-1}+\frac{3}{x+3}-\frac{4}{x+2}\right)\]
\[\boldsymbol{y’=\frac{1}{5}\cdot\frac{12}{(x-1)(x+3)(x+2)}\cdot \sqrt[5]{\frac{(x-1)(x+3)^3}{(x+2)^4}}}\]
対数を取ることによって累乗の部分を前に出せたり積を和の形にバラすことができたりと、計算が簡単になっているのが分かると思います。
正であることが保証されていないと対数を取ることが出来ないので、対数を取る前に両辺の絶対値を取っていることにも注意しましょう。
ただし、積や累乗がたくさん入っているときに対数微分法を使う、というのが実際の入試問題で活きることは経験上ほとんどないので、これは参考程度のものだと思っておけばよいです。
対数微分法で対数を取らない裏技を紹介
対数微分法では、少し記述が長くなってしまいやや面倒です。そこで、対数微分法で対数を取らなくて済む裏技を紹介したいと思います!
$\log$を取った式を$e$の肩に乗せる
$log$を取った式を$e$の肩に乗せて、全く同じ式を作り出すと微分公式が使える形になります。例えば、$x^x$であれば、
\[x^x=e^{\log x^x}=e^{x\log x}\]
です。これは、対数が「底の数を何乗したら真数に等しくなるか」という値に等しいという定義から分かることですよね。
$e^x$の微分公式と合成関数の微分公式を使う!
$e$の肩に乗せる変形ができたら、あとは、$e^x$の微分公式と合成関数の微分公式を使えば微分ができます!
\[\left(e^{x\log x}\right)’=\left(\log x+1\right)x^x\]
対数微分法を使うのと本質的には全く同じなんですが、こちらのほうが少し記述が短くなるのが分かるかと思います。
対数微分法が関わる入試問題3選
対数微分法を理解したら、あとは入試問題を解いて演習を積みましょう!
問題1
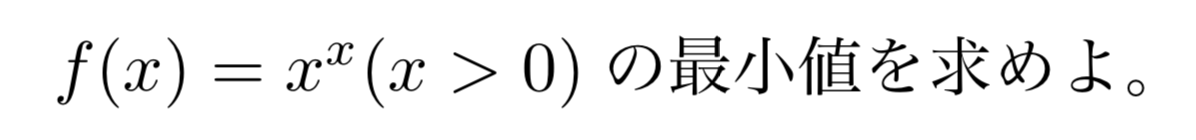
解答・解説
対数微分法を使って$x^x$を微分してあげて、増減表を描いてあげればOKです!
\[(x^x)’=\left(e^{x\log x}\right)’=(1+\log x)x^x\]
より、$f(x)$の増減表は以下のようになる。
\[\begin{array}{|c||c|c|c|c|} \hline x&(0)&\cdots&\frac{1}{e}&\cdots\\\hline f'(x)&&-&0&+\\\hline
f(x)&&\searrow&\left(\frac{1}{e}\right)^{\frac{1}{e}}&\nearrow\\\hline\end{array}\]
したがって、求める最小値は、
\[\boldsymbol{\left(\frac{1}{e}\right)^{\frac{1}{e}}(x=\frac{1}{e}のとき)}\]
問題2

解答・解説
2016年の東大理系数学第一問で出題された問題です。左辺と右辺はどちらも極限が$e$になることはすぐに分かるので、左辺が単調増加することと右辺が単調減少することを示してあげれば証明完了です。
左辺と右辺の関数を微分するときには対数微分法が必要になります。
解説はこの記事を読んでください。
問題3

解答・解説
2018年のお茶の水女子大の問題です。対数微分法を使わないと微分できない関数$f(x)$のグラフを描かせてから、定数分離の考え方を用いた解の個数の議論を(3)でやらせるという構成になっています。定数分離については以下の記事が詳しいです。
(2)で極限を求めるときにも対数を取って議論することに注意しましょう。
扱う関数が複雑になっていること以外は非常にオーソドックスな問題だと言えるでしょう。
以下、解答例です。
(1) $x>0$において、$f(x)=x^{(x^2)}$は常に正であるから、両辺の自然対数をとることができて、
\[\log f(x)=x^2\log x\]
両辺を$x$で微分すると、
\[\frac{f'(x)}{f(x)}=2x\log x+x\]
\[\boldsymbol{f'(x)=x(2\log x+1)x^{(x^2)}}\]
さらにこの両辺を$x$で微分して、
\[f^{\prime\prime}(x)=(3+2\log x)x^{(x^2)}+x^2(2\log x+1)^2x^{(x^2)}\]
\[\boldsymbol{f^{\prime\prime}(x)=\{3+2\log x+x^2(2\log x+1)^2\}x^{(x^2)}}\]
(2)
\[\lim_{x\to +0}\log f(x)=\lim_{x\to +0} x\cdot x\log x=0\]
であるから、
\[\lim_{x\to +0} f(x)=1\]
\[\lim_{x\to +0} f'(x)=(2x\log x+x)f(x)=1\cdot 0=0\]
となる。これと(1)より、$f(x)$の増減表は以下のようになる。
\[\begin{array}{|c||c|c|c|c|} \hline x&(0)&\cdots&\frac{1}{\sqrt{e}}&\cdots\\\hline f'(x)&(0)&-&0&+\\\hline
f(x)&(1)&\searrow&\left(\frac{1}{\sqrt{e}}\right)^{\frac{1}{e}}&\nearrow\\\hline\end{array}\]
したがって、曲線$y=f(x)$のグラフは下図の太線部。(ただし、白丸を含まない。)
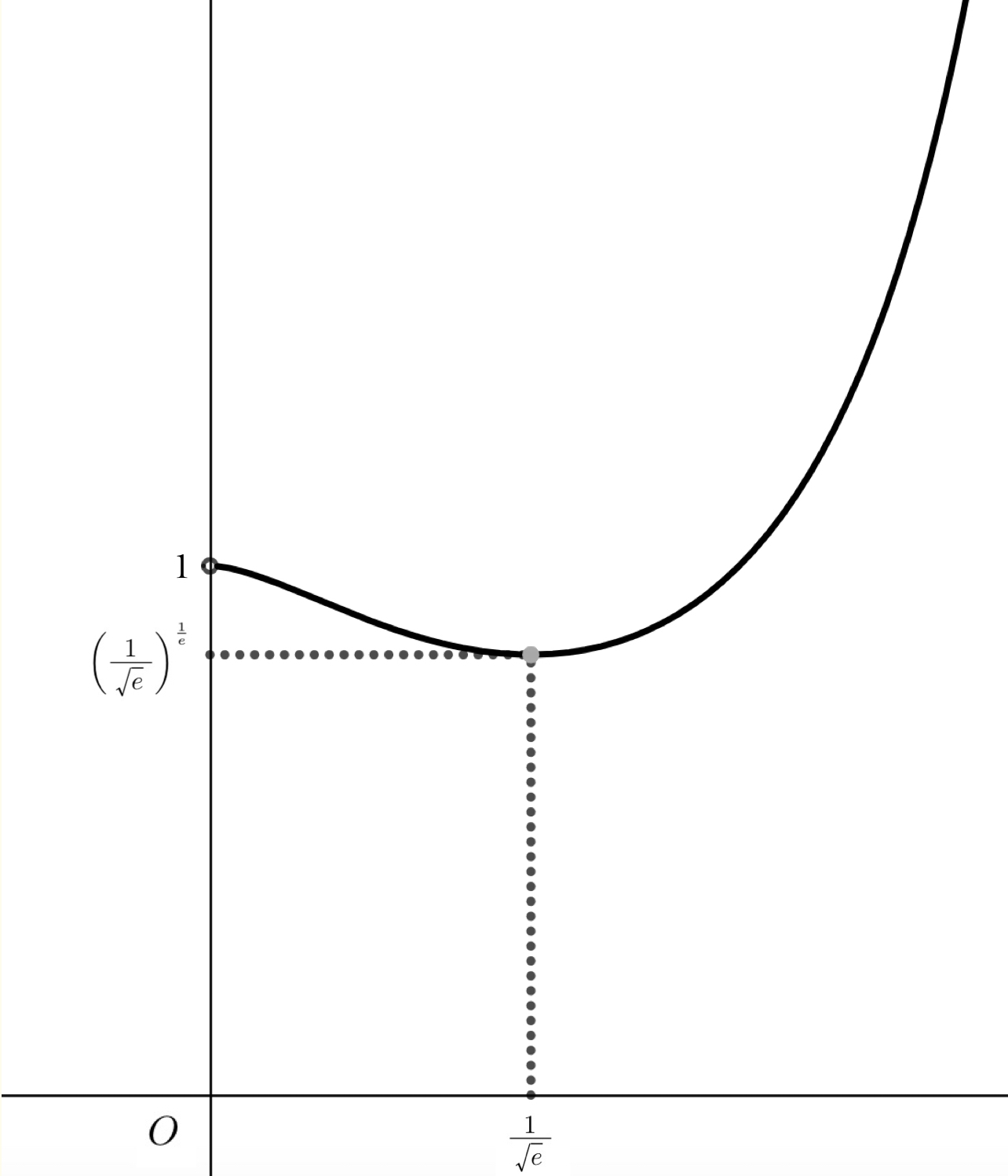
(3) 方程式$f(x)=k$の実数解の個数は$y=f(x)$のグラフと$y=k$のグラフの共有点の個数に等しいので、(2)のグラフより、求める$k$の範囲は、
\[\boldsymbol{\left(\frac{1}{\sqrt{e}}\right)^{\frac{1}{e}}<k<1}\]
まとめ
・対数微分法とは$f(x)^{g(x)}$の形の関数を微分できる手法
・対数を取る時は底は$e$を選べばOK
・対数微分法を使うときは、指数関数の微分公式の証明、$f(x),\,g(x)$が定数関数でない$f(x)^{g(x)}$の形の関数の微分、積や累乗がたくさん出てくる関数の微分の3つ
・$e$の肩に乗せる変形をすれば、記述が少し短くなる