東大医学部生の相談室

合成関数の微分公式は？証明や覚え方を例題付きで東大医学部生が解説！

合成関数の微分公式は？証明や覚え方を例題付きで東大医学部生が解説！

この記事を読むとわかること

・合成関数の微分公式とはなにか

・合成関数の微分公式の覚え方

・合成関数の微分公式の証明

・合成関数の微分公式が関わる入試問題

目次

合成関数の微分公式は？

そもそも合成関数とは

合成関数とは、関数$f$が$x$を$y$に対応させて、関数$g$が$y$を$z$に対応させるとき、$x$を$z$に対応させる関数を$f$と$g$の合成関数と呼び、$g(f(x))$と書きます。

 

例えば、$f(x)=x^2+1,\,g(x)=x^2$であるとき、$g(f(x))=(x^2+1)^2$となります。

合成関数の微分公式は？

合成関数を微分するときには、以下の微分公式が成り立つことが知られています。

合成関数の微分公式

\[\left\{g(f(x))\right\}'=f'(x)g'(f(x))\]

合成関数の微分公式を覚えておくことで、複雑な関数の微分計算を素早く行うことができます。

合成関数の微分公式の覚え方

合成関数の微分公式は「箱の微分に中身を代入したもの×中身の微分」と覚えておくと覚えやすいです。

$f(x)=x^2+1,\,g(x)=x^2$のときに$g(f(x))=(x^2+1)^2$という合成関数の微分をしてみましょう。

 

まず、この合成関数を$g$という箱の中に$f$が入ったものだと捉えます。

「箱の微分に中身を代入したもの」とは箱の微分すなわち$g'(x)=2x$に$f(x)=x^2+1$を代入したものなので、

\[2(x^2+1)\]

のことを指します。

また、「中身の微分」とは箱の中身の微分すなわち$f'(x)=2x$のことを指します。

 

したがって、「箱の微分に中身を代入したもの」と「中身の微分」の積は、

\[2(x^2+1)\cdot 2x=4x(x^2+1)\]

となります。これは展開してから微分したものと一致することが容易に確かめられますね。

合成関数の微分公式の証明

合成関数の微分公式の証明は以下のようになります。以下の証明において、$f$と$g$は連続かつ微分可能な関数を表しています。

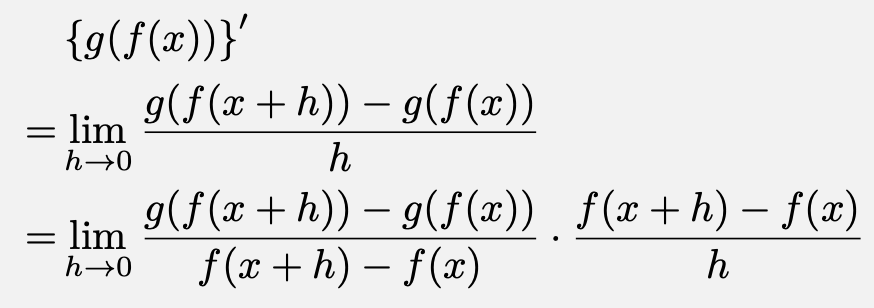
\begin{align*}&\left\{g(f(x))\right\}'\\=&\lim_{h\to 0}\frac{g(f(x+h))-g(f(x))}{h}\\=&\lim_{h\to 0}\frac{g(f(x+h))-g(f(x))}{f(x+h)-f(x)}\cdot\frac{f(x+h)-f(x)}{h}\end{align*}

ここで、$f(x)$は連続であるから、$h\to 0$であれば$f(x+h)-f(x)\to 0$となるから、

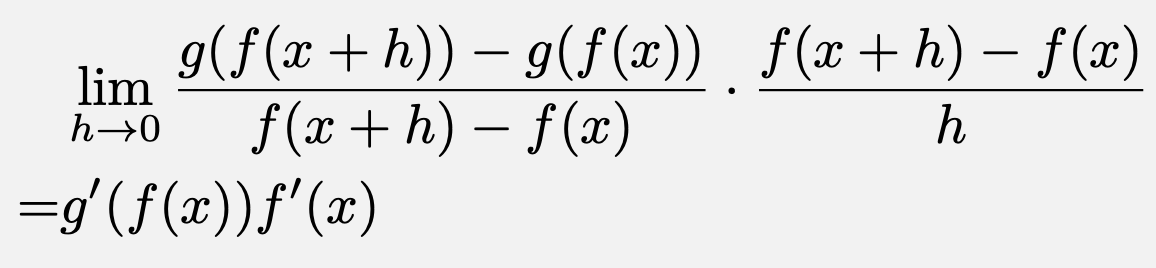
\begin{align*}&\lim_{h\to 0}\frac{g(f(x+h))-g(f(x))}{f(x+h)-f(x)}\cdot\frac{f(x+h)-f(x)}{h}\\=&g'(f(x))f'(x)\end{align*}

定義にしたがって微分する中で、$f(x+h)-f(x)$で割ってかけることにという上手い変形を施すのがポイントとなっています。

合成関数の微分が関わる入試問題

合成関数の微分を理解したら、入試問題を解きましょう！合成関数の微分をするだけの問題というのはなかなか出てこないので、問題を解く中で合成関数の微分の知識が必要になるものを取り上げたいと思います。

問題1

解答・解説

(1)において導関数$f'(x)$を求める際に、合成関数の微分公式を利用する必要があります。$\frac{1}{1+e^{-x}}$を微分する際には、まず、$\frac{1}{x}$という箱と$1+e^{-x}$という中身だとみなして、

\[\left(\frac{1}{1+e^{-x}}\right)'=-\frac{(1+e^{-x})'}{(1+e^{-x})^2}\]

となり、さらに、$e^{-x}$は$e^x$という箱と$-x$という中身でできているものだとみなせば、

\[(e^{-x})'=-e^{-x}\]

となるので、微分が求まりますね。

 

導関数が求まったあとは、相加相乗平均の大小関係を用いて最大値を求めることができます。相加相乗平均の大小関係については以下の記事が詳しいです。

相加相乗平均の大小関係の証明や使い方、入試問題などを解説！

 

(3)は数列の極限に関する問題です。数列の極限を求めるときは、$a_{n+1}$と$a_n$を$x$に置き換えたときの解を両辺から引いた式を作り、$a_n$とその値との差の絶対値が徐々に小さくなっていくという式を作るのでした。

数列の極限値を求める議論はいつも決まりきっているので、流れを覚えておくようにしましょう。

以下、解答例です。

(1)

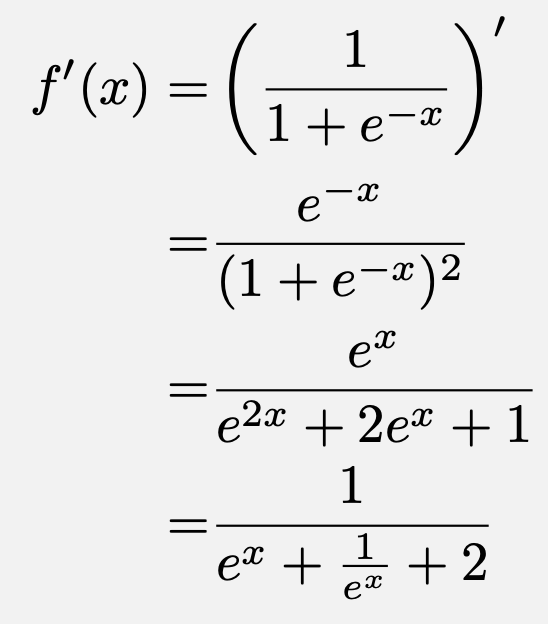
\begin{align*}f'(x)=&\left(\frac{1}{1+e^{-x}}\right)'\\=&\frac{e^{-x}}{(1+e^{-x})^2}\\=&\frac{e^{x}}{e^{2x}+2e^x+1}\\=&\frac{1}{e^x+\frac{1}{e^x}+2}\end{align*}

ここで、$e^x>0$であるから、相加相乗平均の大小関係より、

\[\frac{1}{e^x+\frac{1}{e^x}+2}\leqq \frac{1}{2\sqrt{e^x\cdot \frac{1}{e^x}}+2}=\frac{1}{4}\]

等号成立は、$e^x=\frac{1}{e^x}$つまり$x=0$のとき。

したがって、求める$f'(x)$の最大値は$\boldsymbol{\frac{1}{4}}$

 

(2)　$g(x)=f(x)-x$とおくと、(1)より、

\[g'(x)=f'(x)-1\leqq -\frac{3}{4}<0\]

よって、$g(x)$は単調減少する。また、

\[\lim_{x\to \infty}g(x)=\infty\] \[\lim_{x\to -\infty}g(x)=-\infty\]

で、$g(x)$は連続であるから、方程式$g(x)=0$すなわち方程式$f(x)=x$はただ一つの実数解を持つ。

 

(3)　$f(x)=x$のただ一つの実数解を$\alpha$とおくと、$\alpha=f(\alpha)$であるから、これを$a_{n+1}=f(a_n)$から辺々引いて、

\[a_{n+1}-\alpha=f(a_n)-f(\alpha)\]

ここで、$a_n\ne\alpha$のとき、$f(x)$は全実数で微分可能であるから、平均値の定理より、

\[f(a_n)-f(\alpha)=f'(c_n)(a_n-\alpha)\]

を満たす実数$c_n$が$a_n$と$\alpha$の間に存在する。これを代入して、両辺の絶対値を取ると、

\[|a_{n+1}-\alpha|=|f'(c_n)||a_n-\alpha|\]

となる。ここで、(1)より$f'(x)$は常に正で、最大値が$\frac{1}{4}$であるので、

\[|f'(c_n)|\leqq \frac{1}{4}\]

が言える。これと$|a_n-\alpha|>0$より、

\[|a_{n+1}-\alpha|=\frac{1}{4}|a_n-\alpha|\]

$a_n=\alpha$のときもこれは成り立つ。この式を繰り返し用いれば、

\[|a_n-\alpha|\leqq \left(\frac{1}{4}\right)^{n-1}|a_1-\alpha|\]

となる。よって、

\[0\leqq |a_n-\alpha|\leqq \left(\frac{1}{4}\right)^{n-1}|a_1-\alpha|\] \[\lim_{n\to \infty}\left(\frac{1}{4}\right)^{n-1}|a_1-\alpha|=0\]

より、はさみうちの原理から、

\[\lim_{n\to \infty}|a_n-\alpha|=0\]

すなわち、

\[\lim_{n\to \infty}a_n=\alpha\]

が言える。したがって、題意成立。

問題2

解答・解説

積の微分や合成関数の微分を用いる問題になります。2つ関数の大小を考えるときには、差を取って微分をすればうまくいくことが多いのでした。

2つの関数$f(x),\,g(x)$について$f(x)>g(x)$がなりたつことを示すときには、$f(x)-g(x)$を微分して常に$0$より大きいことを示す流れがうまくいくことが多い

しかし、この問題では単純に差を取って微分をしているだけでは行き詰まってしまいます。なぜなら、何回微分をしても指数関数と三角関数が混在している状況から抜け出せないからです。

 

そこで、両辺に$e^{-\frac{x^2}{2}}$をかけて、$e^{\frac{x^2}{2}}\cos{x}$の形にすると、微分したあとの式を$e^{\frac{x^2}{2}}$でくくることができ、三角関数のみが含まれた部分を作り出すことができます。

指数関数と三角関数が混在した式を微分したいなら、指数関数×三角関数の形にしてから！

この知識がないと、延々と微分をして何をしていけばいいのかわからなくなってしまうので、難易度としては難しいと言えるでしょう。

 

$e^{\frac{x^2}{2}}$を微分するときには、$e^x$が箱で、$\frac{x^2}{2}$が中身になるので、合成関数の微分を用いると、

\[(e^{\frac{x^2}{2}})'=xe^{\frac{x^2}{2}}\]

と計算できます。

 

答案は以下のようになります。

\[e^{-\frac{x^2}{2}}>\cos{x}\]

の両辺に$e^{\frac{x^2}{2}}(>0)$をかけて、

\[e^{\frac{x^2}{2}}\cos{x}<1\]

よって、この不等式が$0<x<\frac{\pi}{2}$において成立することを示せばよい。

左辺を$f(x)$とすると、

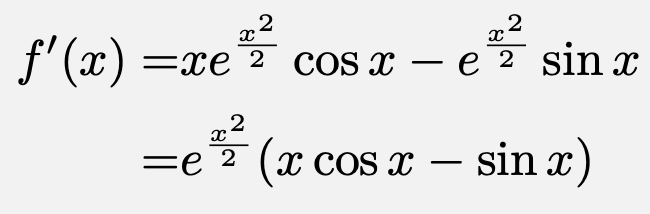
\begin{align*}f'(x)=&xe^{\frac{x^2}{2}}\cos{x}-e^{\frac{x^2}{2}}\sin{x}\\=&e^{\frac{x^2}{2}}(x\cos{x}-\sin{x})\end{align*}

$e^{\frac{x^2}{2}}>0$であることから、$g(x)=x\cos{x}-\sin{x}$とおくと、$f^{\prime}(x)$の符号と$g(x)$の符号は一致する。

\[g'(x)=-x\sin{x}+\cos{x}-\cos{x}=-x\sin{x}\]

これは、$0<x<\frac{\pi}{2}$において常に負であるので、$g(x)$は単調減少し、

\[g(x)<g(0)=0\]

よって、$f^{\prime}(x)<0$が分かるので、$f(x)$は単調減少し、

\[f(x)<f(0)=1\]

が成り立つ。したがって、題意成立。

まとめ

・合成関数とは2つの関数を順に作用させるのをまとめて一つの関数とみなしたもの

・合成関数$g(f(x))$を微分すると$f'(x)g'(f(x))$となる

・「箱の微分に中身を代入したもの×中身の微分」と覚えておくとよい

・合成関数の微分公式の証明は$f(x+h)-f(x)$で割ってかけるという変形がポイント

数Ⅲカテゴリの最新記事