この記事を読むと分かること
・複素数平面の反転とは何か
・反転の有名な性質
・反転に関する入試問題3題
複素数平面の反転とは?
複素数平面における反転とは、ある点を表す複素数$z$を、
\[w=\frac{1}{\bar{z}}\]
で定まる複素数$w$が表す点へとうつす変換のことを指します。
反転の幾何的な解釈
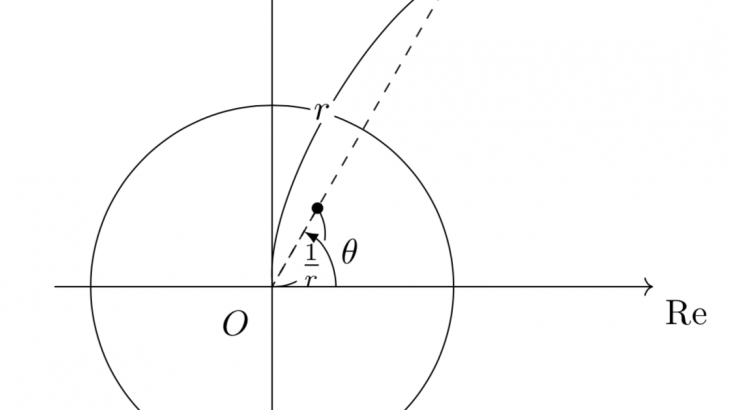
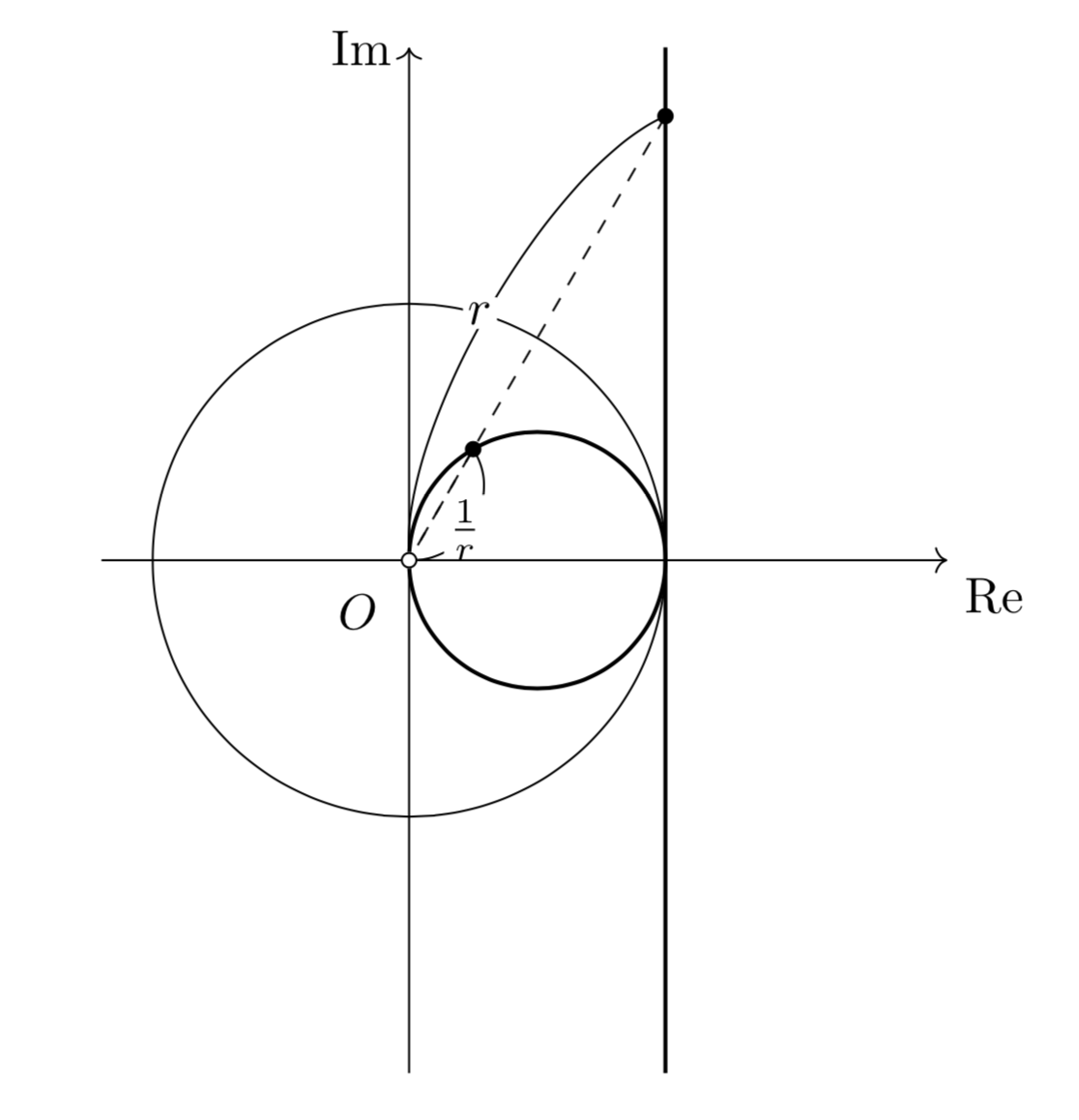
このままだと反転が何なのかわからないと思うので、$z=r(\cos\theta+i\sin\theta)$と極形式で表した時に$w$がどんな点を表すのか見てみましょう。
$\bar{z}=r\left\{\cos(-\theta)+i\sin(-\theta)\right\}$を$w=\frac{1}{\bar{z}}$に代入すると、\[w=\frac{1}{\bar{z}}=\frac{1}{r}(\cos\theta+i\sin\theta)\]
となるので、以下の図のような対応関係になっていることがわかります。
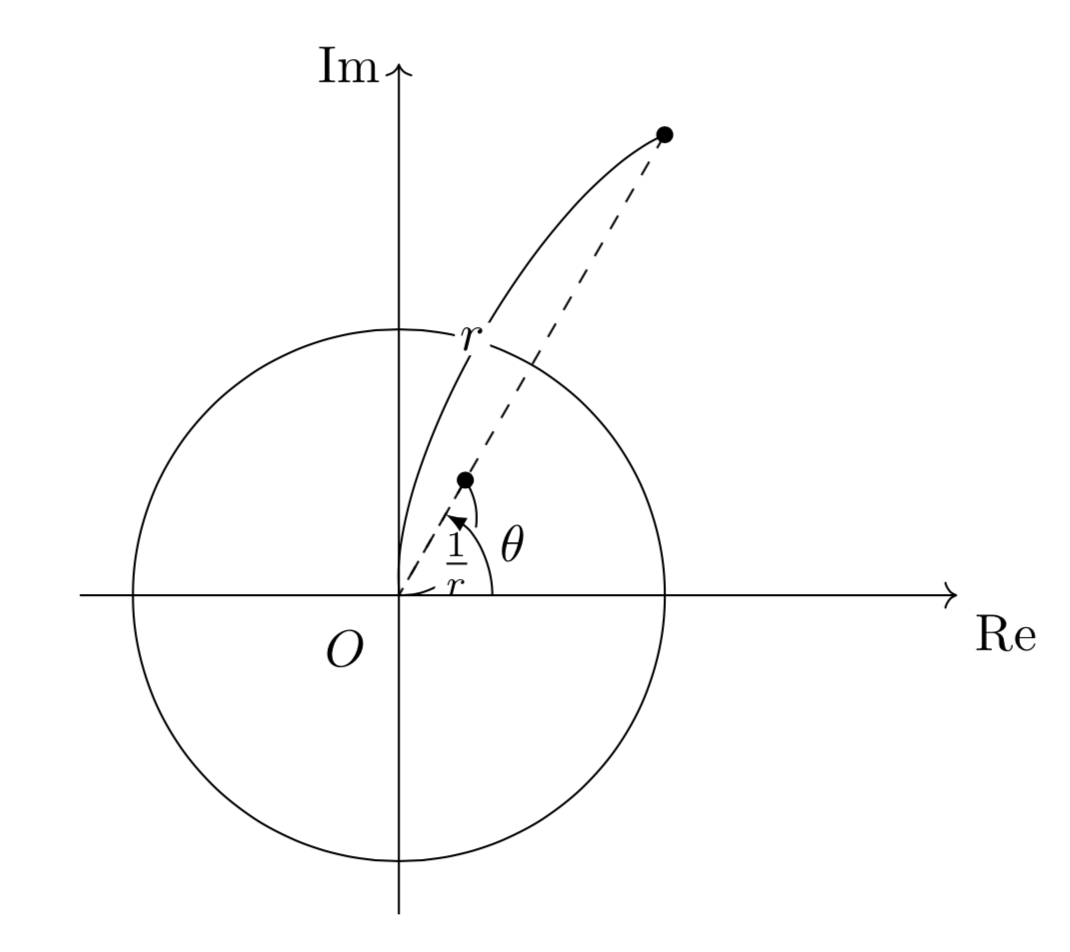
よって、「ある点$\mathrm{P}$を反転変換すると、半直線$\mathrm{OP}$上にある、$\mathrm{OP}\cdot\mathrm{OQ}=1$をみたす点$\mathrm{Q}$にうつる」というのが幾何的な解釈になります。
入試問題で複素数平面の反転は頻出
新課程になってから行列の代わりに複素数平面が出題されるようになりましたが、複素数平面では回転変換の道具として登場するだけでなく、反転変換に関する話題もよく入試で出題されます。
先程は1点に対しての反転変換を考えましたが、入試問題では「ある図形上の点すべてに反転変換したときにどのような図形が出てくるのか」という軌跡の問題としてよく登場します。
$w=\frac{1}{z}$など、上で説明した変換と全く同じではないものの非常によく似た変換が出てくることが多いんですが、以下で説明するような反転に関する性質は共通なので、覚えておくとよいでしょう。
反転に関する有名な性質
どのような図形を反転させると何の図形になるのか、という対応関係のうち、以下の2つ覚えておくと、入試問題において答えの予想がつくようになります!
反転に関する有名な性質2つ!
1.原点を通る円⇄原点を通らない直線
2.原点を通らない円⇄原点を通らない円
※反転の反転は元の図形になるので、“A⇄B”はAを反転させればBになり、Bを反転させればAになることを表しています。
これらの性質について見ていきましょう!
原点を通る円⇄原点を通らない直線
原点を通る円を反転させると原点を通らない直線になり、原点を通らない直線を反転させると原点を通る円になります。
原点を通る円は、中心に対応する複素数を$p(\ne 0)$とすれば、
\[|z-p|=|p|\]
と表せるので、$z\ne0$において、$z=\frac{1}{\bar{w}}$を代入すると、
\[\left|\frac{1}{\bar{w}}-p\right|=|p|\Leftrightarrow \left|w-\frac{1}{\bar{p}}\right|=|w|\]
となります。これは$\frac{1}{\bar{p}}$と$0$からの距離が等しいことを表しているので、その2点を結ぶ線分の垂直二等分線上を$z$は動くことがわかります。
この対応を図示すると以下のようになります。
原点に限りなく近い点は、無限遠点に対応し、次の項で説明する円同士の対応も考えると、「原点を通る円は半径が$\infty$の円(つまり直線)に対応する」と捉えることもできますね。
ちなみに、原点を通る直線は先程の幾何的な解釈を考えれば、もちろん同じ直線にうつることがわかります。
原点を通らない円⇄原点を通らない円
原点を通らない円は原点を通らない円に対応します。
原点を通らない円は中心を表す複素数を$c$、半径を$r(\ne |c|)$とすれば、
\[|z-c|=r\]
となるので、$z=0$とはならないことに注意して、$z=\frac{1}{\bar{w}}$を代入すると、
\[\left|\frac{1}{\bar{w}}-c\right|=r\Leftrightarrow |\bar{c}w-1|=r|w|\]
両辺$0$以上であるから2乗しても同値で、$r\ne |c|$に注意して変形していくと、
\[\begin{align*}&|\bar{c}w|^2-\bar{c}w-c\bar{w}+1=r^2|w|^2\\\Leftrightarrow &(|c|^2-r^2)|w|^2-\bar{c}w-c\bar{w}+1=0\\\Leftrightarrow &\left|w-\frac{c}{|c|^2-r^2}\right|^2=\frac{r^2}{(|c|^2-r^2)^2}\end{align*}\]
よって、$\frac{c}{|c|^2-r^2}$を中心とする、半径$\frac{r}{||c|^2-r^2|}$の円に対応することがわかります。
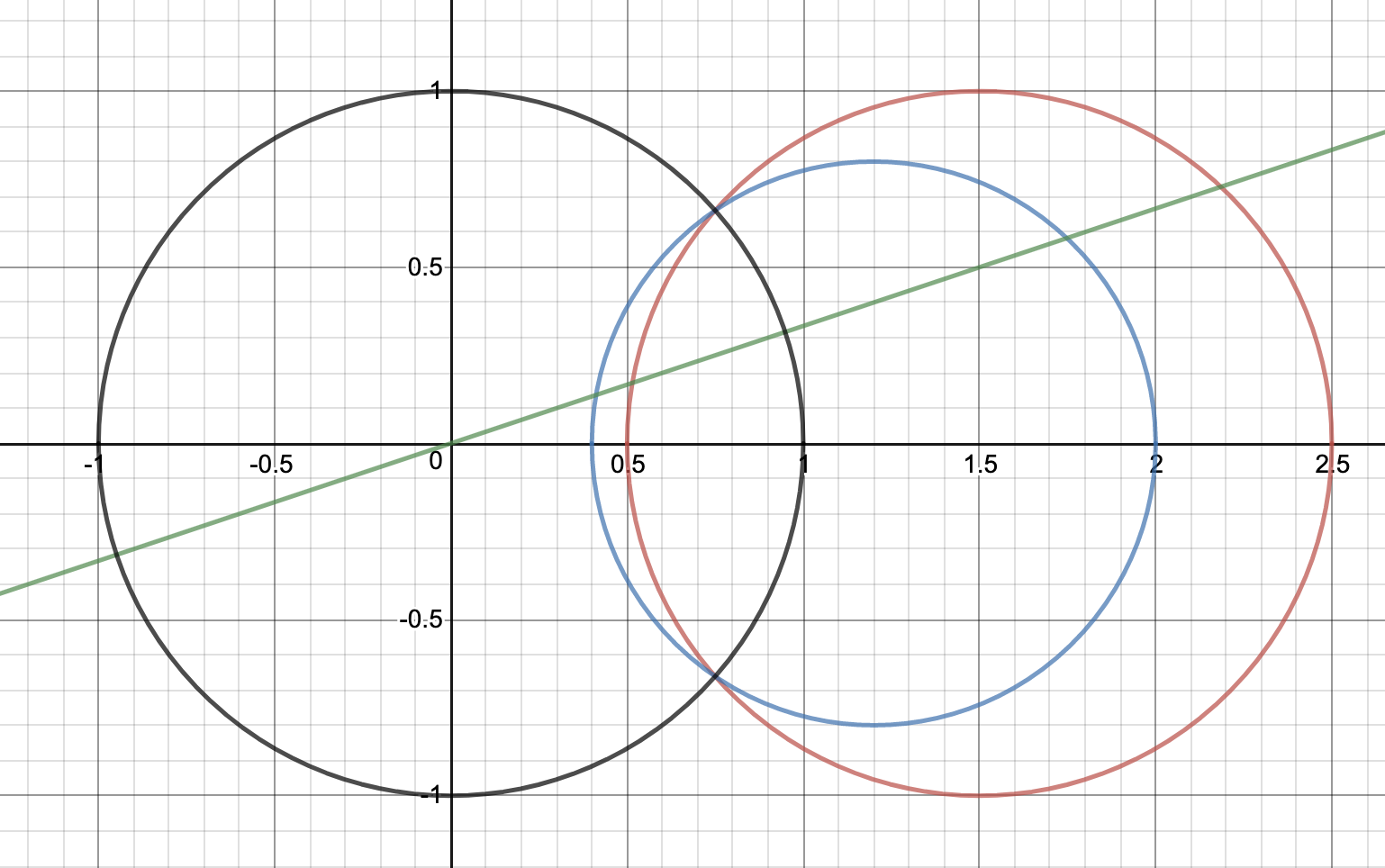
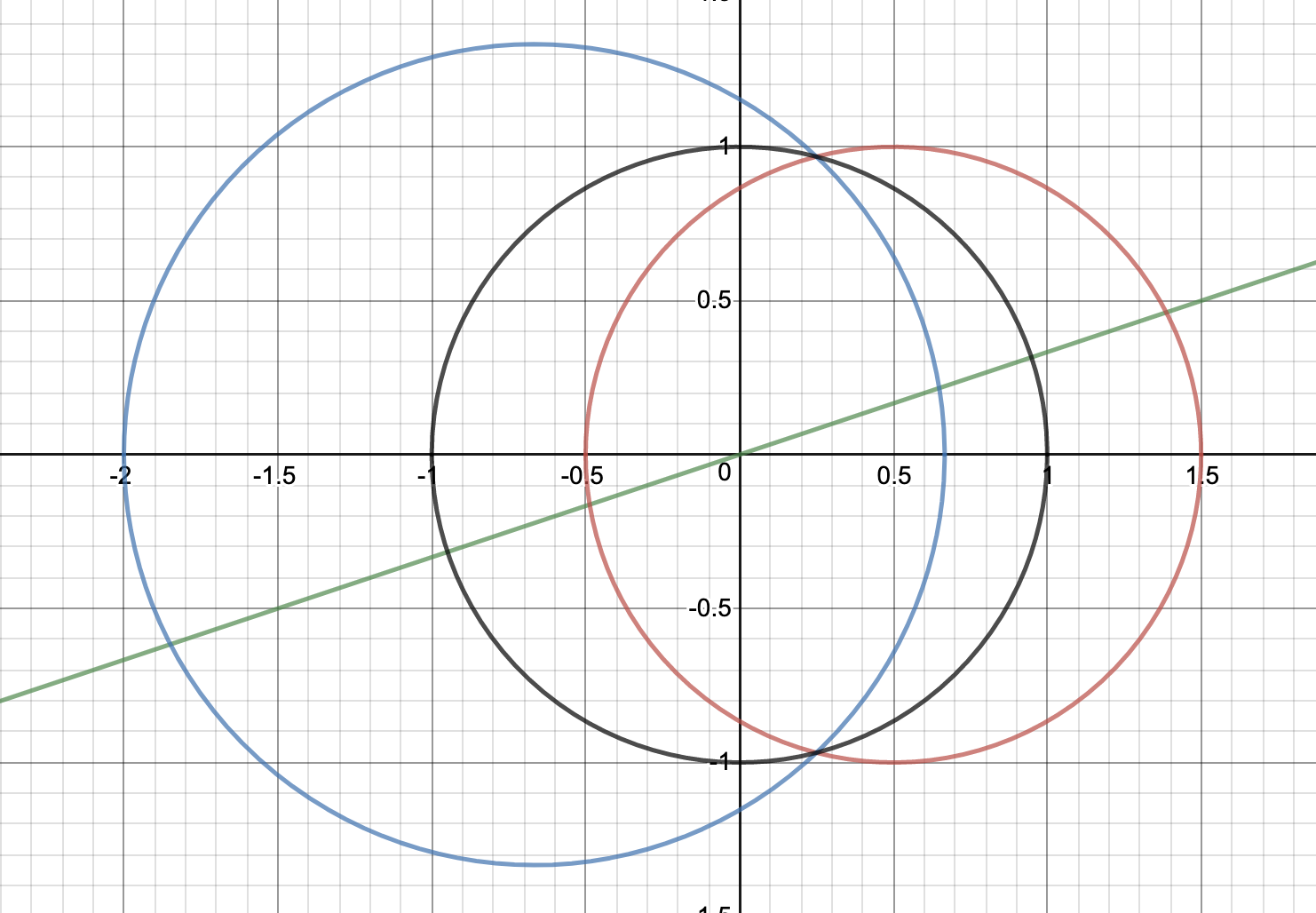
この対応を図示すると以下のようになります。(赤を反転変換すると青になります。)
原点が円の内部にない場合↓
原点が円の内部にある場合↓
反転が関わる入試問題3選
反転に関する入試問題は非常によく出題されます。
そこで、反転が関わる入試問題を3つ取り上げて、それぞれの問題について解説していきたいと思います!
問題1

解答・解説
(1)は幾何的な説明で反転が定義されたものを複素数の関係式で表す問題です。この記事とは逆の説明の順番になってますが、特に問題なく解けるでしょう。
(2)では、点$\mathrm{P}$が原点を通らない円周上を動くので、反転の性質から点$\mathrm{Q}$も原点を通らない円周上にうつることがすぐに分かりますね。
このように、反転の性質を覚えておくだけで求めるべき軌跡の形がわかることがあるので、反転の性質は覚えておくと得です。
以下、解答例です。
点$\mathrm{Q}$は半直線$\mathrm{OP}$上にあるので、正の実数$k$を用いて、
\[w=kz\]
と表すことができる。ここで、$\mathrm{OP}\cdot\mathrm{OQ}=1$より、$z\ne 0$において、
\[|z|\cdot|kz|=1\Leftrightarrow k=\frac{1}{|z|^2}\]
また、$z=0$のときは、条件をみたすような点$\mathrm{Q}$をとることができない。
したがって、$k=\frac{1}{|z|^2}$を代入して、
\[w=\frac{z}{|z|^2}\Leftrightarrow \boldsymbol{w=\frac{1}{\bar{z}}(z\ne 0)}\]
(2) 点$\mathrm{P}$は$2$を中心とする半径$\sqrt{3}$の円周上を動くので、
\[|z-2|^2=3\]
をみたす。また、$w\ne 0$であるので、(1)より、
\[w=\frac{1}{\bar{z}}\Leftrightarrow z=\frac{1}{\bar{w}}\]
これを上の式に代入して、$w\ne 0$に注意して変形すると、
\[\begin{align*}&\left|\frac{1}{\bar{w}}-2\right|^2=3\\\Leftrightarrow &|w|^2-2w-2\bar{w}+1=0\\\Leftrightarrow &|w-2|^2=3\end{align*}\]
したがって、点$\mathrm{Q}$は$2$を中心とする半径$\sqrt{3}$の円周上を動く。これを複素数平面上に図示すると下図の太線部。
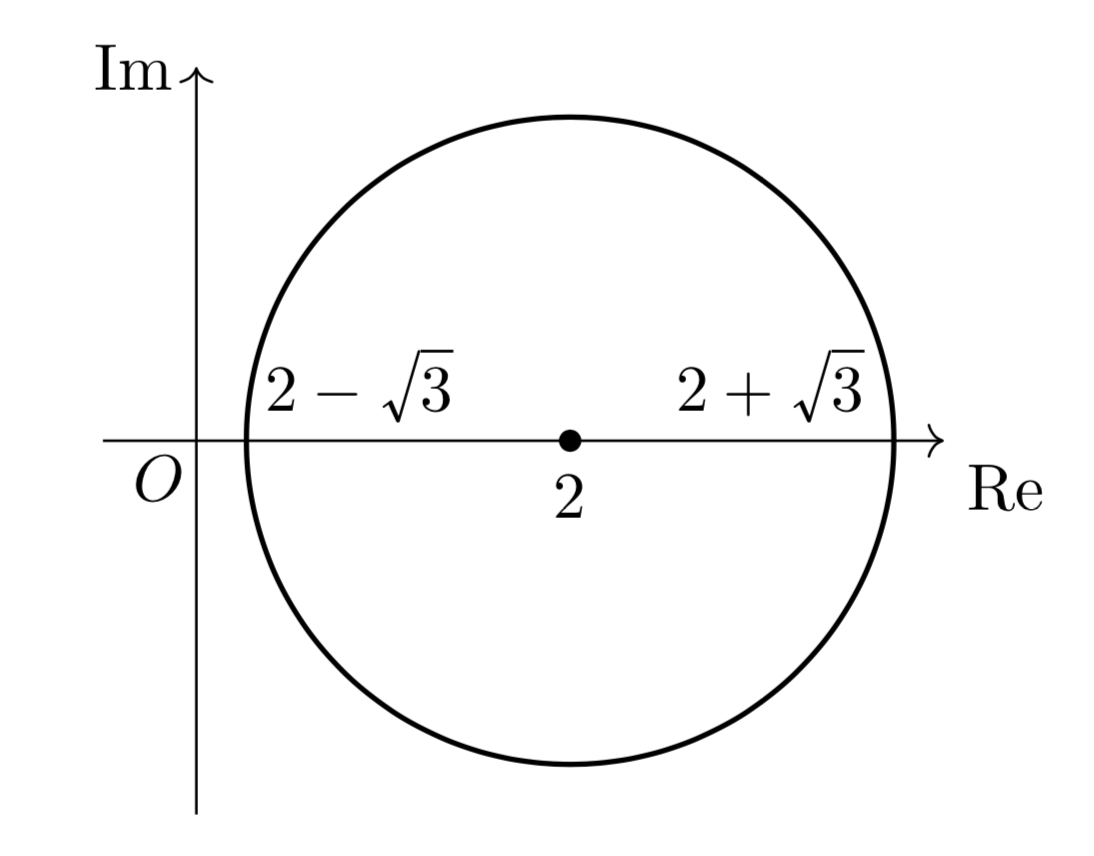
今回は実軸上に円の中心があって、実軸と円が交わるところの値の積が$1$になっていることから、反転によって得られた円も全く同一の円になるという少し特殊な状況でした。
問題2

解答・解説
反転変換を拡張した「鏡像の関係」に関する問題です。この問題において、$r=1$とした場合が上で説明した反転ですね。
(1)では、円の中心が$\alpha$となっているので、図形全体を$-\alpha$だけ平行移動してあげれば、普通の反転とほとんど変わらなくなります。
(2)以降は少し特殊な問題で、反転させる点が移動するのではなく、反転円が移動したときに$i$はどのような図形にうつるか、という問題になっています。(2)で$x,\,y$を$\alpha$の関数として表しているので、$\alpha$を消去してあげれば軌跡は求まりますね。
円が動くのは以下の動画のような様子ですね。

円の中心が直線上を動くことから、反転の性質から求める軌跡が円になるのではないかとなんとなく予想がつくかと思います。
実際、鏡像の関係にある点も含めた動画は以下のようになり、円周上を動くことがわかりますね!

このようにして、反転の性質から求める軌跡がどのようになるか予想を立ててから問題に取り組むとミスが少なくなるのでおすすめです。
あとは、軌跡のうちどの範囲を動くのかにも注意しましょう。
以下、解答例になります。
(1) 図形全体を$-\alpha$だけ平行移動すると、以下の図ようになる。
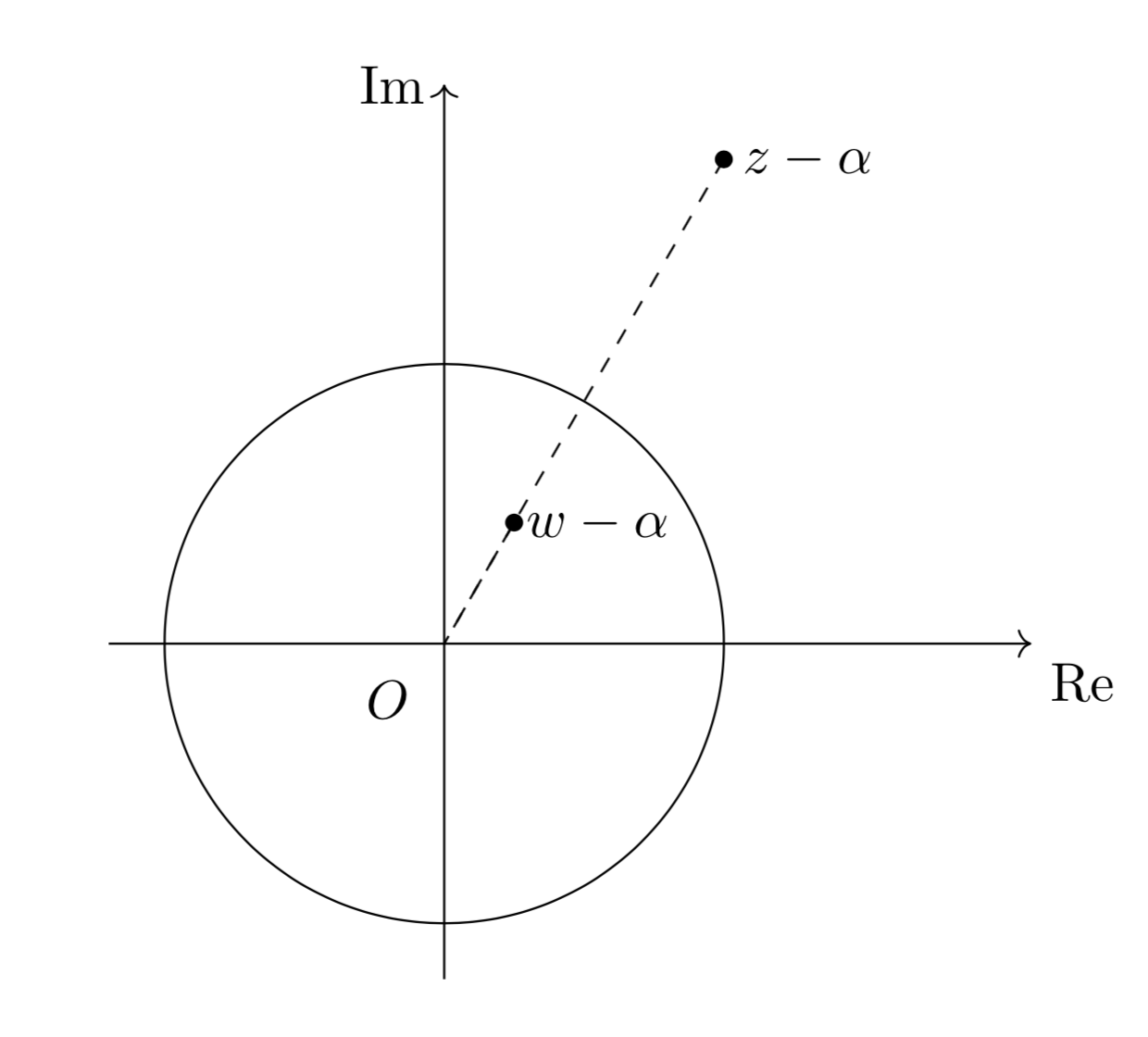
$w-\alpha$は$\mathrm{O}$と$z-\alpha$を結んだ半直線上にあるので、正の実数$k$を用いて、
\[w-\alpha=k(z-\alpha)\]
と表すことができる。また、鏡像の関係にあることから、
\[|w-\alpha|\cdot|z-\alpha|=\alpha^2\]
も成り立つので、上の式を代入して、$z\ne \alpha$のとき、
\[k|z-\alpha|^2=\alpha^2\Leftrightarrow k=\frac{\alpha^2}{|z-\alpha|^2}\]
これを代入すると、
\[w-\alpha=\frac{\alpha^2}{|z-\alpha|^2}\cdot(z-\alpha)\Leftrightarrow w=\frac{\alpha\bar{z}}{\bar{z}-\alpha}\]
また、$z=\alpha$のときは、鏡像の関係を定義できない。
したがって、
\[\boldsymbol{f_{\alpha}(z)=\frac{\alpha\bar{z}}{\bar{z}-\alpha}(z\ne \alpha)}\]
(2) (1)で求めた式に$z=i$を代入して、
\[f_{\alpha}(i)=\frac{-\alpha i}{-i-\alpha}=\frac{\alpha}{\alpha^2+1}+\frac{\alpha^2}{\alpha^2+1}i\]
よって、
\[\boldsymbol{x=\frac{\alpha}{\alpha^2+1},\,y=\frac{\alpha^2}{\alpha^2+1}}\]
(3) $x=\frac{\alpha}{\alpha^2+1},\,y=\frac{\alpha^2}{\alpha^2+1}$より、
\[\alpha=\frac{y}{x}\]
であるから、これを$x=\frac{\alpha}{\alpha^2+1}$に代入して、
\[x=\frac{\frac{y}{x}}{(\frac{y}{x})^2+1}\Leftrightarrow x^2+\left(y-\frac{1}{2}\right)^2=\frac{1}{4}\]
ここで、$\alpha$は正の数であるから、
\[\frac{dx}{d\alpha}=\frac{1-\alpha^2}{(\alpha^2+1)^2}\]
\[\frac{dy}{d\alpha}=\frac{2\alpha}{(\alpha^2+1)^2}\]
より、増減表は以下のようになる。
\[\begin{array}{|c||c|c|c|c|c|} \hline \alpha&(0)&\cdots&1&\cdots&(\infty)\\\hline\frac{dx}{d\alpha}&1&+&0&-&0\\\hline
\frac{dy}{d\alpha}&0&+&1&+&0\\\hline (x,\,y)&(0,\,0)&\nearrow&\left(\frac{1}{2},\,\frac{1}{2}\right)&\nwarrow&(0,\,1)\\\hline\end{array}\]
したがって、求める軌跡は、
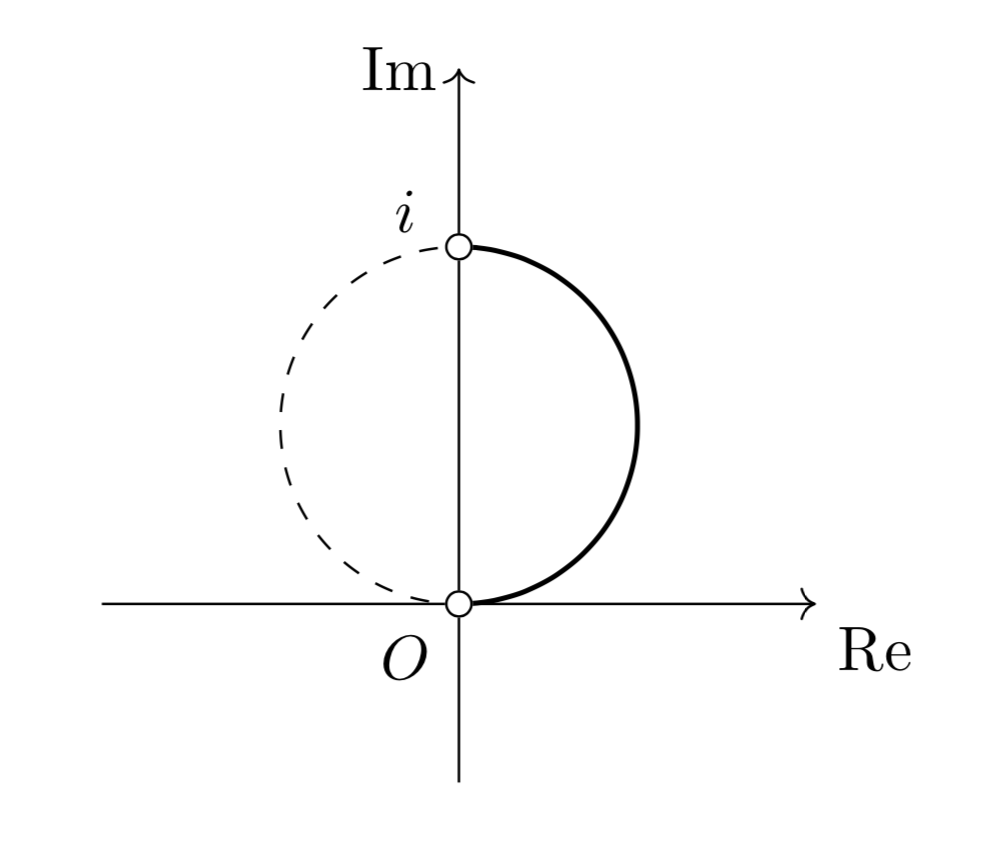
\[\boldsymbol{x^2+\left(y-\frac{1}{2}\right)^2=\frac{1}{4}(x>0)}\]
これを複素数平面上に図示すると以下の太線部。(ただし白丸を含まない)
問題3

解答・解説
反転と全く同じ変換でなくとも、
\[w=\frac{1}{z}\]
という変換であれば、反転の性質は同じように使えます。(1)(2)で求めるのは、直線、線分の上を$z$が動くときの$w$の軌跡なので、どちらも何らかの円の円周上にあることはすぐにわかりますね。
これは2017年度東大理系数学第三問で出題された問題です。詳しい解説はこちら↓
まとめ
・反転とは$w=\frac{1}{\bar{z}}$という変換のこと
・幾何的には、ある点Pをとったときに半直線OP上にあって、OP・OQ=1をみたす点Qへの変換のこと
・原点を通らない直線を反転させると原点を通る円に、原点を通る円を反転させると原点を通らない直線になる
・原点を通らない円を反転させると原点を通らない円になる
・反転の性質を覚えておくと入試問題で答えの予想がある程度つくようになる