媒介変数表示されたグラフの面積の求め方を例題付きで解説！検算に使える定理も教えます！

この記事を読むとわかること

・媒介変数表示されたグラフで囲まれた面積の求め方

・媒介変数表示されたグラフで囲まれた面積を求める入試問題

・検算に使える定理とその証明

媒介変数表示されたグラフの面積の求め方は？

媒介変数表示されたグラフによって囲まれた面積の求め方は以下の3つの手順によって求めることができます！

媒介変数表示されたグラフの面積は、

1.パラメータで微分してグラフの概形を描く

2.積分の式を立てる

3.パラメータで置換積分する

という手順で求まる！

パラメータで微分してグラフの概形を描く

グラフの概形を把握しなければ面積を求めることはできません。なぜなら、面積は積分によって求めますが、グラフがわからなければ積分区間も分からず、また、 $x$ 軸よりも上にあるか下にあるかがわからなければ符号もわからないからです。

そこで、まずは、パラメータで微分をして増減表を描き、グラフの概形を描くという作業が必須になります。

媒介変数表示されたグラフの描き方について詳しく説明した記事はこちら。

積分の式を立てる

グラフの概形がわかったら、それを元にして積分の形で面積を求める式を立式します。 $x$ 軸よりも下側にある部分は積分によって負の値として面積が求まり、 $x$ 軸よりも上側の場合は正の値として面積が求まることに注意しましょう。

このときには、計算量を減らすために対称性にも注意しましょう。例えば、下図のような形のグラフで囲まれた面積を求める場合には、 $x$ 軸に関する対称性があるため、 $x$ 軸の上側の部分の面積を求めてから2倍してあげればいいですよね。

(グラフを描くときにも対称性に注意していると描くべき増減表が少なくて済みます。)

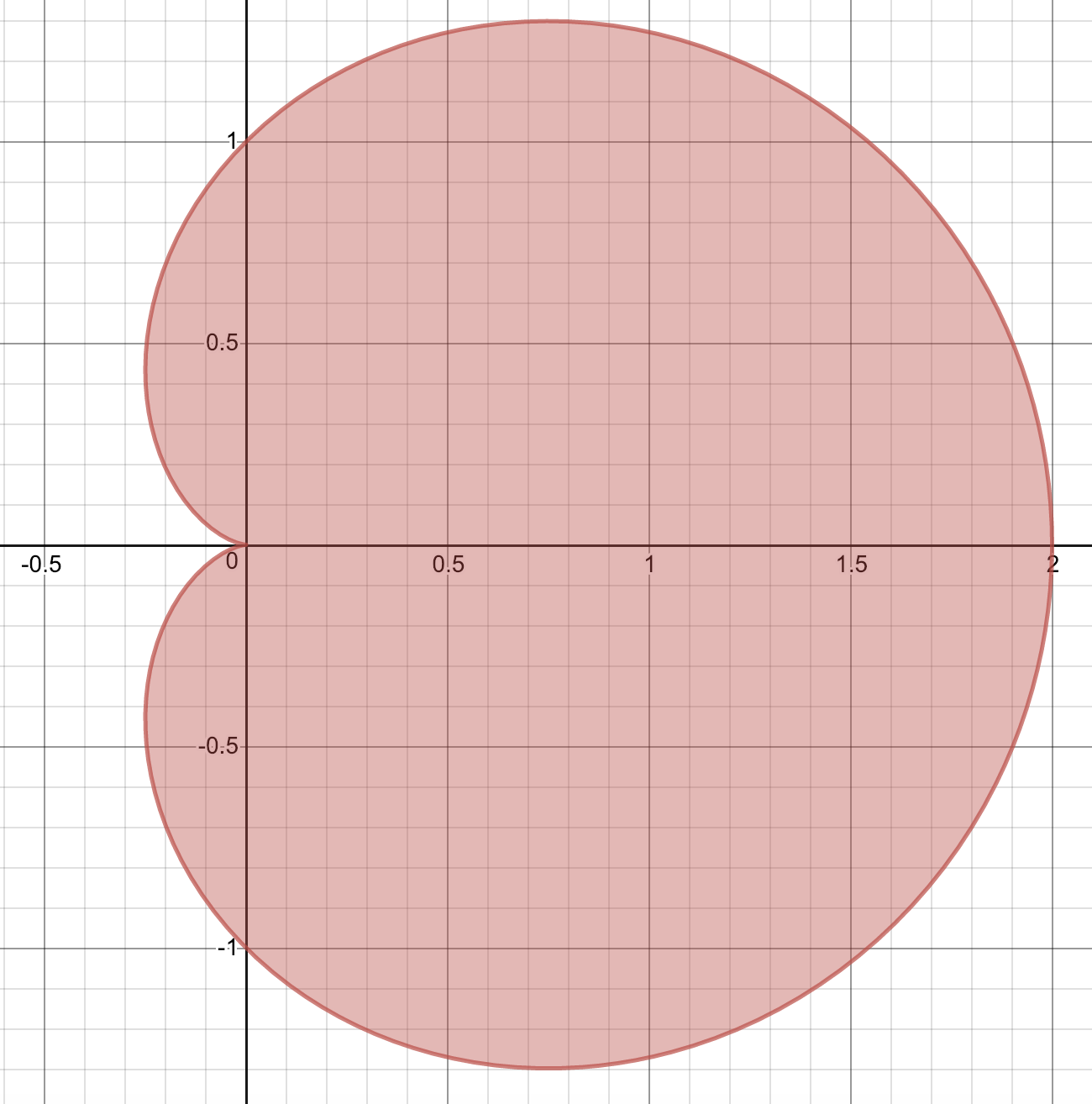
このようにして、立式の段階で計算量が減るような工夫をするよう心がけましょう。

パラメータで置換積分する

積分の式が立ったら、パラメータによって置換積分をしてあげます。つまり、

$\left\{\begin{array}{l}x=f(t)\\y=g(t)\end{array}\right.$

という形で媒介変数表示されていた場合には、これを用いて置換積分を実行します。積分する方向に対してグラフが単調に変化しない場合には、置換積分の際に積分区間を分ける必要があることに注意しましょう。

媒介変数表示されたグラフの面積を求める入試問題

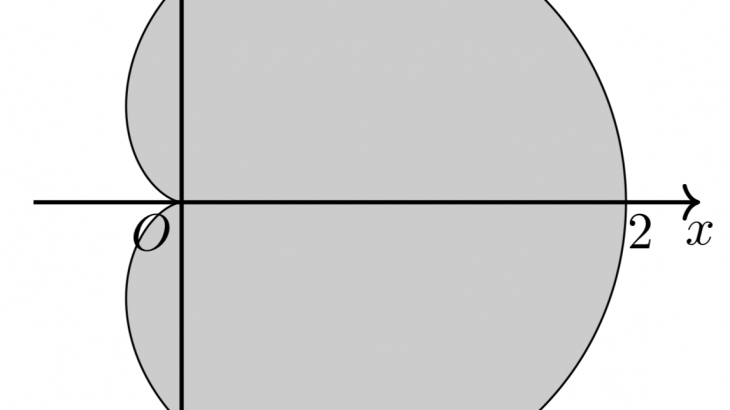
実際に出題される入試問題を解いてみると上の説明への理解がぐっと深まるでしょう。今回は、カージオイドとアステロイドという有名な曲線に囲まれた部分の面積を求めてみましょう。

例題1(カージオイド)

問題

$\left\{\begin{array}{l}x=\cos t(1+\cos t)\\y=\sin t(1+\cos t)\end{array}\right.(0\leqq t\leqq 2\pi)$

で表される曲線で囲まれた部分の面積を求めよ。

解答

$\cos (2\pi -t)\{1+\cos(2\pi -t)\}=\cos t(1+\cos t)$

$\sin(2\pi -t)\{1+\cos(2\pi -t)\}=-\sin t(1+\cos t)$

であることから、 $0\leqq t\leqq\pi$ の部分を $x$ 軸に関して折り返すことによって題意の曲線は得られる。

ここで、

\begin{align*}&\left\{\begin{array}{l}\frac{dx}{dt}=-\sin t(1+2\cos t)\\\frac{dy}{dt}=\cos t+\cos 2t\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}\frac{dx}{dt}=-\sin t(1+2\cos t)\\\frac{dy}{dt}=2\cos \frac{3}{2}t\cos \frac{1}{2}t\end{array}\right.\end{align*}

であるから、 $0\leqq t\leqq\pi$ の範囲における増減表は以下のようになる。

\begin{array}{|c|c|c||c|c|c|c|c|} \hline t&0&\cdots&\frac{\pi}{3}&\cdots&\frac{2}{3}\pi&\cdots&\pi\\\hline\frac{dx}{dt}&0&-&-&-&0&+&+\\\hline \frac{dy}{dt}&+&+&0&-&-&-&-\\\hline (x,\,y)&(2,\,0)&\nwarrow&\left(\frac{3}{4},\,\frac{3\sqrt{3}}{4}\right)&\swarrow&\left(-\frac{1}{4},\,\frac{\sqrt{3}}{4}\right)&\searrow&(0,\,0)\\\hline\end{array}

よって、 $x$ 軸に関する対称性も考慮すると、グラフの概形は以下ようになる。

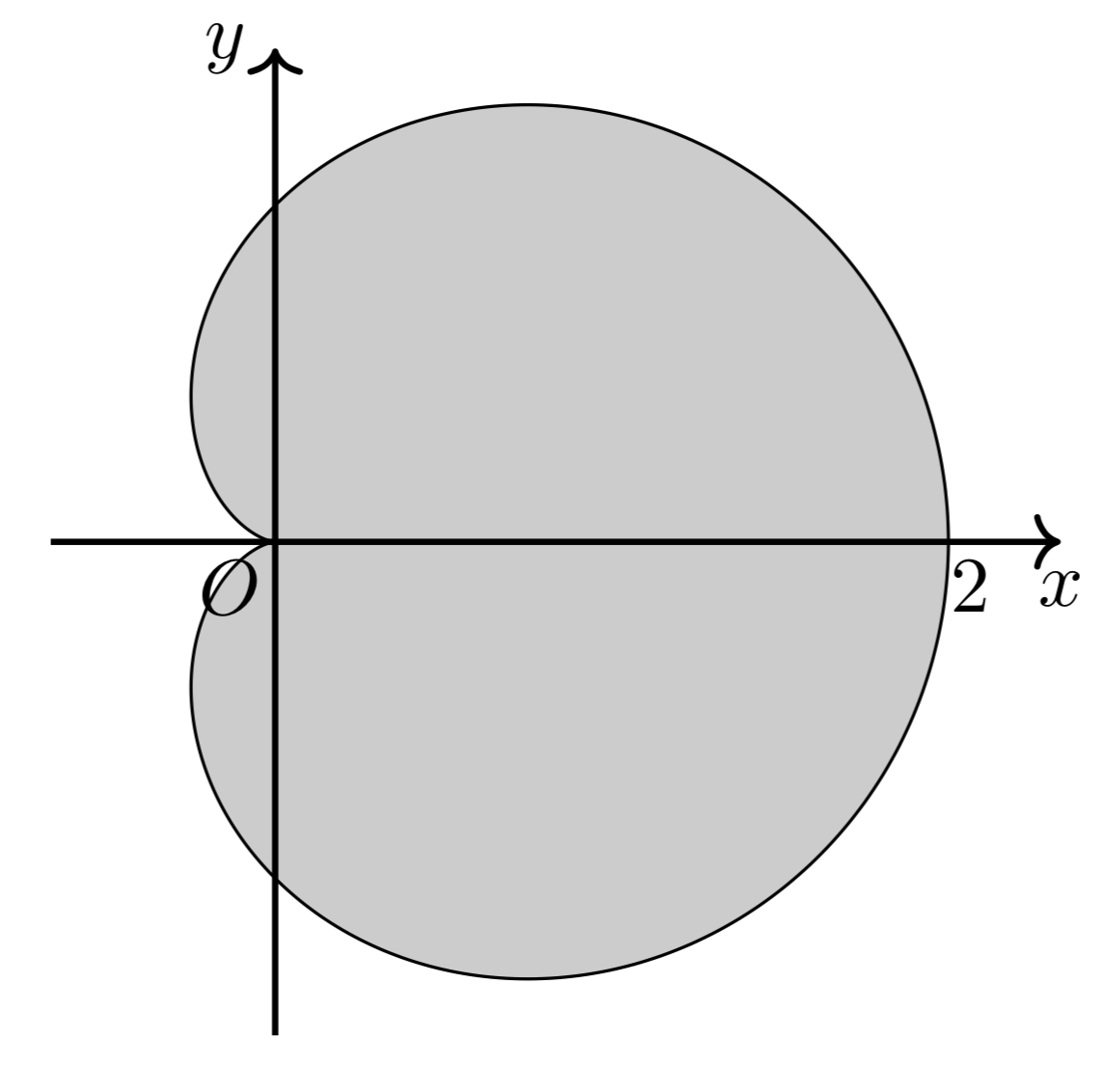
したがって、 $0\leqq t\leqq\frac{2}{3}\pi$ のときの $y$ 座標を $y^+$ 、 $\frac{2}{3}\pi\leqq t\leqq\pi$ の $y$ 座標を $y^-$ とすれば、求める面積の半分は、

\begin{align*}&\int_{-\frac{1}{4}}^{2}y^+dx-\int_{-\frac{1}{4}}^{0}y^-dx\\=&\int_{\frac{2}{3}\pi}^{0}\sin t(1+\cos t)(-\sin t)(1+2\cos t)dt-\int_{\frac{2}{3}\pi}^{\pi}\sin t(1+\cos t)(-\sin t)(1+2\cos t)dt\\=&\int_{0}^{\pi}\{\sin^2 t+3\sin^2 t\cos t+2\sin^2 t\cos^2 t \}dt\\=&\int_{0}^{\pi}\left\{\frac{1-\cos 2t}{2}+3\sin^2 t\cos t+\frac{1}{2}\sin^2 2t \right\}dt\\=&\int_{0}^{\pi}\left\{\frac{1-\cos 2t}{2}+3\sin^2 t\cos t+\frac{1-\cos 4t}{4} \right\}dt\\=&\left[\frac{3}{4}t-\frac{1}{4}\sin 2t+\sin^3 t-\frac{1}{16}\sin 4 t\right]^{\pi}_{0}\\=&\frac{3}{4}\pi\end{align*}

したがって、求める面積はこの2倍で、 $\boldsymbol{\frac{3}{2}\pi}$

議論の流れが、

1. $x$ 軸に関する対称性があることを述べる

2.パラメータ微分をして増減表を描く

3.対称性も考慮してグラフの概形を描く

4.積分の式を立てて置換積分する

となっていることが分かると思います。

積分するときに覚えておきたいのは、パラメータ $t$ に対して $x$ が増加するときと減少するときを分けて立式するものの、置換積分をしたときには積分区間が必ず繋がるという点です。上の問題で言えば、

$\int_{-\frac{1}{4}}^{2}y^+dx-\int_{-\frac{1}{4}}^{0}y^-dx$

という場合分けがなされた積分だったものが、置換積分をしたあとには、

$\int_{0}^{\pi}\{\sin^2 t+3\sin^2 t\cos t+2\sin^2 t\cos^2 t \}dt$

という1つの積分にまとまっています。

このポイントを覚えておくと、計算が少し楽になるはずです。

例題2(アステロイド)

問題

$\left\{\begin{array}{l}x=\cos^3 t\\y=\sin^3 t\end{array}\right.(0\leqq t\leqq 2\pi)$

で表される曲線で囲まれた部分の面積を求めよ。

解答

$\cos^3 (2\pi-t)=\cos^3 t$

$\sin^3 (2\pi-t)=-\sin^3 t$

であることから、 $0\leqq t\leqq\pi$ の部分を $x$ 軸に関して折り返すことによって題意の曲線は得られる。

さらに、

$\cos^3 (\pi-t)=-\cos^3 t$

$\sin^3 (\pi-t)=\sin^3 t$

であることから、 $0\leqq t\leqq\frac{\pi}{2}$ の部分を $y$ 軸に関して折り返すことによって、曲線の $0\leqq t\leqq\pi$ の部分が得られる。

ここで、

$\left\{\begin{array}{l}\frac{dx}{dt}=-3\cos^2 t\sin t\\\frac{dy}{dt}=3\sin^2 t\cos t\end{array}\right.$

であるから、 $0\leqq t\leqq\frac{\pi}{2}$ の範囲における増減表は以下のようになる。

\begin{array}{|c||c|c|c|} \hline t&0&\cdots&\frac{\pi}{2}\\\hline\frac{dx}{dt}&0&-&0\\\hline \frac{dy}{dt}&0&+&0\\\hline (x,\,y)&(1,\,0)&\nwarrow&(0,\,1)\\\hline\end{array}

よって、 $x$ 軸、 $y$ 軸に関する対称性も考慮すると、グラフの概形は以下のようになる。

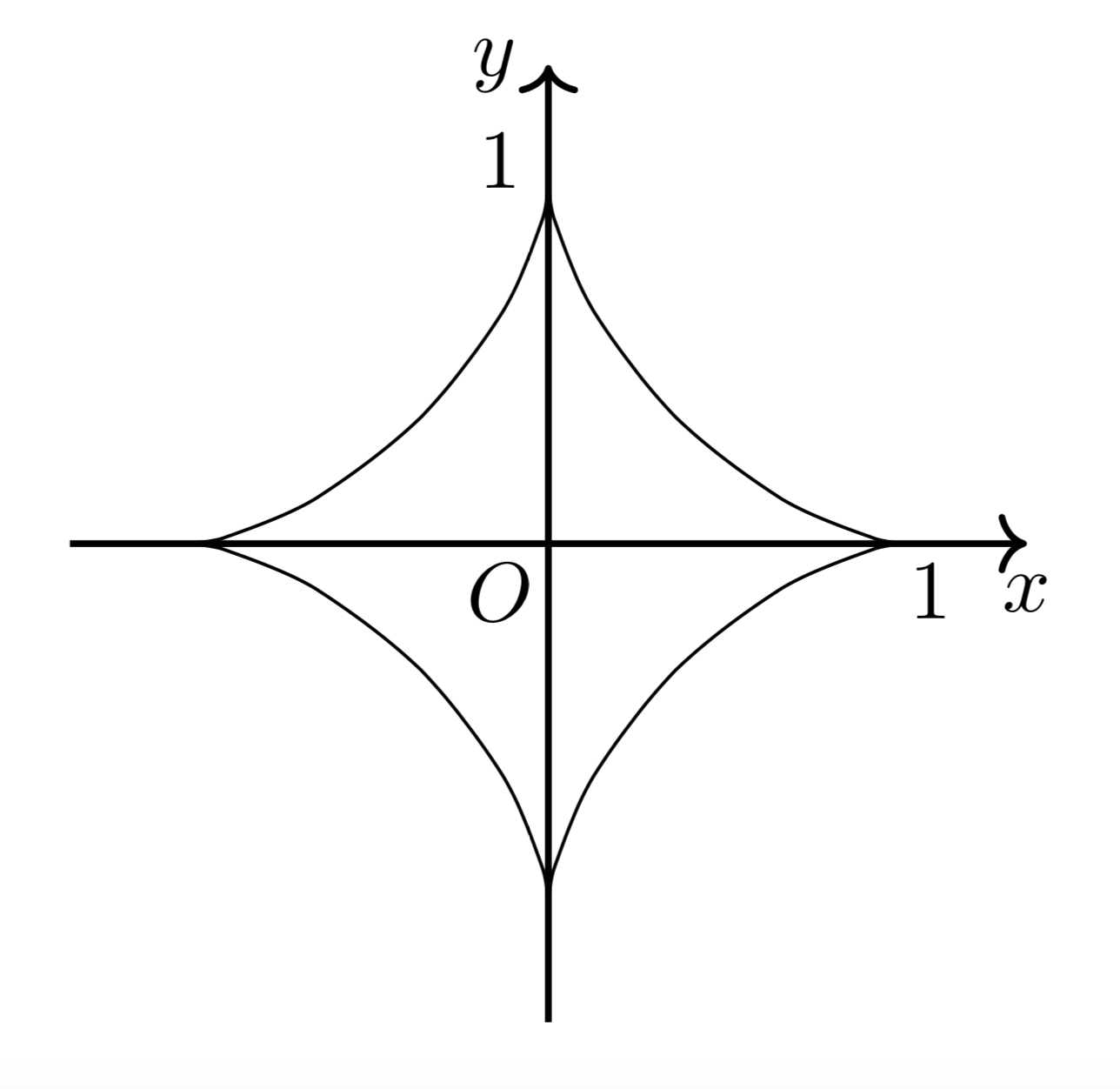
したがって、 $0\leqq t\leqq\frac{\pi}{2}$ のときの $y$ 座標を $y^+$ とすれば、求める面積の $\frac{1}{4}$ は、

\begin{align*}&\int_{0}^{1} y^+dx\\=&\int_{\frac{\pi}{2}}^{0} \sin^3 t(-3\cos^2 t\sin t)dt\\=&3\int^{\frac{\pi}{2}}_{0} \cos^2 t\sin^4 tdt\\=&3\int^{\frac{\pi}{2}}_{0} (1-\sin^2 t)\sin^4 tdt\\=&3\int^{\frac{\pi}{2}}_{0} (\sin^4 t-\sin^6 t)dt\end{align*}

ここで、 $0$ 以上の自然数 $n$ に対して、

$I_n=\int_0^{\frac{\pi}{2}} \sin^n tdt$

とおくと、 $n\geqq 2$ のとき、

\begin{align*}&I_n\\=&\int_0^{\frac{\pi}{2}} \sin t\sin^{n-1} tdt\\=&\left[-\cos t\sin^{n-1}t\right]_{0}^{\frac{\pi}{2}}+(n-1)\int_0^{\frac{\pi}{2}} \cos^2 t\sin^{n-2} tdt\\=&(n-1)\int_0^{\frac{\pi}{2}} (1-\sin^2 t)\sin^{n-2} tdt\\=&(n-1)I_{n-2}-(n-1)I_n\end{align*}

よって、これを整理して、

$I_n=\frac{n-1}{n}I_{n-2}$

が成立する。これを繰り返し用いて、

$\int^{\frac{\pi}{2}}_{0} \sin^4 tdt=\frac{3}{4}\int^{\frac{\pi}{2}}_{0} \sin^2 tdt=\frac{3}{8}\int^{\frac{\pi}{2}}_{0} dt=\frac{3}{16}\pi$

$\int^{\frac{\pi}{2}}_{0} \sin^6 tdt=\frac{5}{6}\int^{\frac{\pi}{2}}_{0} \sin^4 tdt=\frac{5}{32}\pi$

となるので、

\begin{align*}3\int^{\frac{\pi}{2}}_{0} (\sin^4 t-\sin^6 t)dt=&3\left(\frac{3}{16}\pi-\frac{5}{32}\pi\right)\\=&\frac{3}{32}\pi\end{align*}

求める面積はこの4倍で、 $\boldsymbol{\frac{3}{8}\pi}$

今回は $x$ 軸に関しても $y$ 軸に関しても対称になっていることに気づくとかなり計算量が減らせるようになっています。

ただ、置換積分をしたあとの計算がやや面倒です。三角関数の $n$ 乗の積分は、部分積分と漸化式を用いてあげることによって、上のように計算を楽にすることができます。これは、証明の過程も含めて入試で頻出なので覚えておいて損はないでしょう。

媒介変数表示されたグラフの面積の検算方法

媒介変数表示されたグラフによって囲まれた面積の求める過程は計算が複雑であり、計算ミスが頻発しがちです。けれど、入試において計算ミスは許されませんから、検算ができるようになっておくと正答率がぐっと上がり、気持ちが楽になるはずです。

そこで、媒介変数表示されたグラフの面積の検算方法について教えたいと思います！

ガウスグリーンの定理が有効！

媒介変数表示されたグラフに囲まれた面積は、ガウスグリーンの定理というものを用いると実は非常に簡単に計算できることが多いです。ガウスグリーンの定理とは以下のような定理です。

ガウスグリーンの定理

$\left\{\begin{array}{l}x=f(t)\\y=g(t)\end{array}\right.(\alpha\leqq t\leqq\beta)$

と媒介変数表示されたグラフがあって、 $t$ の増加に伴って、原点から見て反時計回りに点 $(f(t),\,g(t))$ が動くとき、動径の掃いた部分の面積は、

$\frac{1}{2}\int_{\alpha}^{\beta}\left(f(t)g'(t)-f'(t)g(t)\right)dt$

で求まる。

つまり、パラメータに伴って反時計まわりに動いてるグラフに囲まれた部分の面積なら、簡単に積分の式が立つよ、ということです。ちなみに、時計回りに動いているときには、マイナスをつければ面積になります。これを用いて上の例題2つの検算をしてみましょう。

まず、カージオイドの場合は原点から見て反時計回りに変化していっているので、ガウスグリーンの定理が使えて、

\begin{align*}& \frac{1}{2}\int_{0}^{2\pi}\left\{\cos t(1+\cos t)(\cos t+\cos 2t)+\sin t(1+2\cos t)\sin t(1+\cos t)\right\}dt\\=& \frac{1}{2}\int_{0}^{2\pi}\left\{\cos t(1+\cos t)(2\cos^2 t+\cos t-1)+(1-\cos ^2 t)(1+2\cos t)(1+\cos t)\right\}dt\\= & \frac{1}{2}\int_{0}^{2\pi}(\cos^2 t+2\cos t+1)dt\\= & \frac{1}{2}\int_{0}^{2\pi}\left(\frac{1+\cos 2t}{2}+2\cos t+1\right)dt\\=&\frac{1}{2}\left[\frac{3}{2}t+\frac{1}{4}\sin 2t+2\sin t\right]_{0}^{2\pi}\\=&\boldsymbol{\frac{3}{2}\pi}\end{align*}

となり、答えが正しいことが確かめられます。

次に、アステロイドについても、ガウスグリーンの定理が使えて、

\begin{align*}& \frac{1}{2}\int_{0}^{2\pi}\left(3\cos^4 t\sin^2 t+3\cos^4 t\sin^2 t\right)dt\\=& \frac{3}{2}\int_{0}^{2\pi}\sin^2t\cos^2 tdt\\= & \frac{3}{2}\int_{0}^{2\pi}\frac{1}{4}\sin^2 2tdt\\= & \frac{3}{8}\int_{0}^{2\pi}\frac{1-\cos 4t}{2}dt\\=&\frac{3}{16}\left[t-\frac{1}{4}\sin 4t\right]_{0}^{2\pi}\\=&\boldsymbol{\frac{3}{8}\pi}\end{align*}

となり、非常に簡単に検算ができることがわかります。

ガウスグリーンの定理によって計算がどの程度簡単になるかは問題にもよりますが、最初の方針とは違うやり方で計算をしなおすときに使いやすい道具として覚えておくべきでしょう。

ガウスグリーンの定理の証明

ガウスグリーンの定理は高校数学では習わないので、答案に使うのは極力避けておくべきです。どうしても使わなければならない場合には証明をしてから使うのが良いでしょう。証明は以下のようになります。

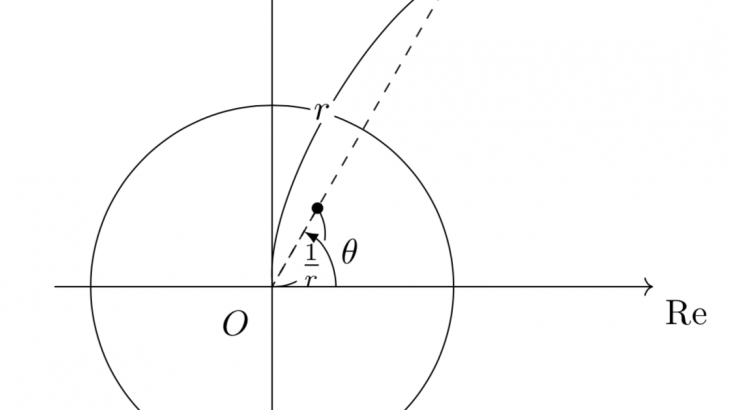
パラメータ $t$ が $t$ から $t+\Delta t$ まで動くときに動径が掃く微小部分の面積について考える。

$t$ から $t+\Delta t$ まで動くときに動径の長さが増加している場合と減少している場合の2通りが考えられるが、増加している以下の図のような場合についてまず考える。

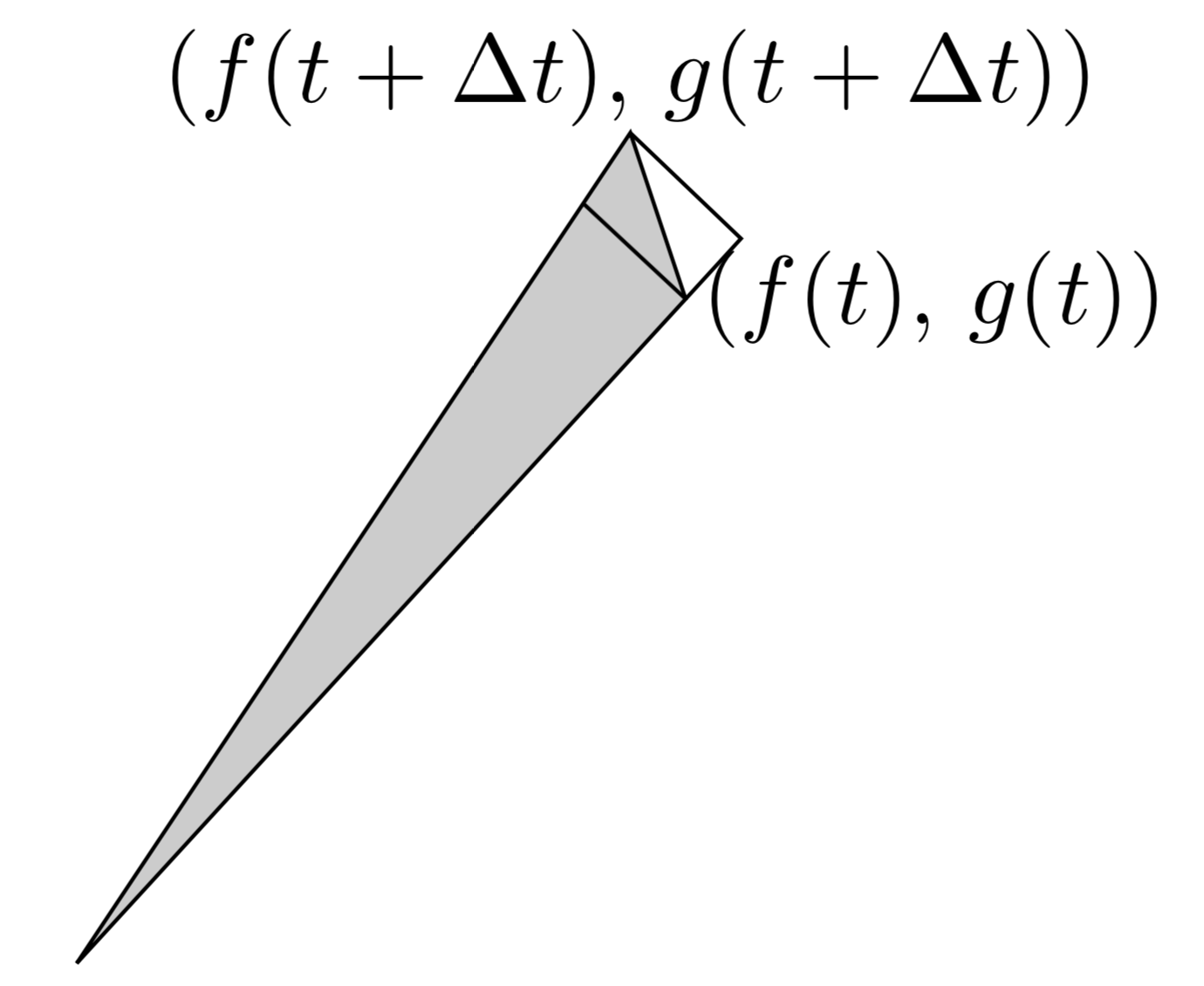
このとき、斜線部の三角形は2つの二等辺三角形に挟まれており、小さい方の三角形のもう1つの頂点は

$\left(\frac{\sqrt{\{f(t)\}^2+\{g(t)\}^2}}{\sqrt{\{f(t+\Delta t)\}^2+\{g(t+\Delta t)\}^2}}f(t+\Delta t),\,\frac{\sqrt{\{f(t)\}^2+\{g(t)\}^2}}{\sqrt{\{f(t+\Delta t)\}^2+\{g(t+\Delta t)\}^2}}g(t+\Delta t)\right)$

であり、その三角形の面積は、

\begin{align*}\frac{\sqrt{\{f(t)\}^2+\{g(t)\}^2}}{2\sqrt{\{f(t+\Delta t)\}^2+\{g(t+\Delta t)\}^2}}\left|f(t)g(t+\Delta t)-f(t+\Delta t)g(t)\right|\end{align*}

ここで、 $t$ が増加するときに反時計周りに動いているならば、外積の $z$ 成分は正になるので、 $f(t)g(t+\Delta t)-f(t+\Delta t)g(t)>0$ が成り立つ。よって、さらに変形して、

\begin{align*}&\frac{\sqrt{\{f(t)\}^2+\{g(t)\}^2}}{2\sqrt{\{f(t+\Delta t)\}^2+\{g(t+\Delta t)\}^2}}\left(f(t)g(t+\Delta t)-f(t+\Delta t)g(t)\right)\\=&\frac{\sqrt{\{f(t)\}^2+\{g(t)\}^2}}{2\sqrt{\{f(t+\Delta t)\}^2+\{g(t+\Delta t)\}^2}}\left(f(t)\frac{g(t+\Delta t)-g(t)}{\Delta t}-\frac{f(t+\Delta t)-f(t)}{\Delta t}g(t)\right)\Delta t\end{align*}

となる。

同様にして、大きい方の二等辺三角形の面積は、

$\frac{\sqrt{\{f(t+\Delta t)\}^2+\{g(t+\Delta t)\}^2}}{2\sqrt{\{f(t)\}^2+\{g(t)\}^2}}\left(f(t)\frac{g(t+\Delta t)-g(t)}{\Delta t}-\frac{f(t+\Delta t)-f(t)}{\Delta t}g(t)\right)\Delta t$

となる。 $\Delta t\rightarrow 0$ の極限を取ると、はさみうちの定理から、斜線部の面積を $S$ とすれば、

$\frac{dS}{dt}=\frac{1}{2}\left(f(t)g'(t)-f'(t)g(t)\right)$

が分かる。

$t$ から $t+\Delta t$ まで動くときに動径の長さが減少している場合も同様に示せる。

したがって、 $\alpha\leqq t\leqq \beta$ の範囲を動くときは、これを積分して、

$\frac{1}{2}\int_{\alpha}^{\beta}\left(f'(t)g(t)-f(t)g'(t)\right)dt$

証明の中で外積が登場していますが、これは高校数学の範囲外の知識になります。外積について詳しく説明した記事はこちら。

ガウスグリーンの定理を用いるにあたっての注意点

ガウスグリーンの定理を用いるときの注意点としては、グラフがパラメータの増加に対して反時計回りに変化しているかという点です。ただし。時計周りに変化している場合でもマイナスをつければ面積になるという点も押さえておきましょう。

さらに言えば、グラフが閉じた曲線で反時計回りに動いているのであれば、原点を中心に見たときに反時計回りに動いていないとしてもその内側の面積は、ガウスグリーンの定理で一発で求めることができます。なぜなら、反時計回りに動いているときに動径が掃く部分の面積から時計回りに動いているときに動径が掃く部分の面積を除かなければなりませんが、それは時計回りのときに負の面積が求まれば問題ないからです。

したがって、閉じた曲線の内側の面積を求める検算のときにはガウスグリーンの定理によってパラメータの端から端まで積分し、もし負の値が求まってしまったらその絶対値を考えればよいことになります。

まとめ

・媒介変数表示されたグラフの内側の面積は

1.パラメータで微分してグラフの概形を描く

2.積分の式を立式する

3.パラメータで置換積分する

の3ステップで求められる

・対称性に気づくと、グラフを描くとき、積分するときに楽になる

・パラメータで置換したあとは必ず積分区間が繋がる

・検算にはガウスグリーンの定理が有効