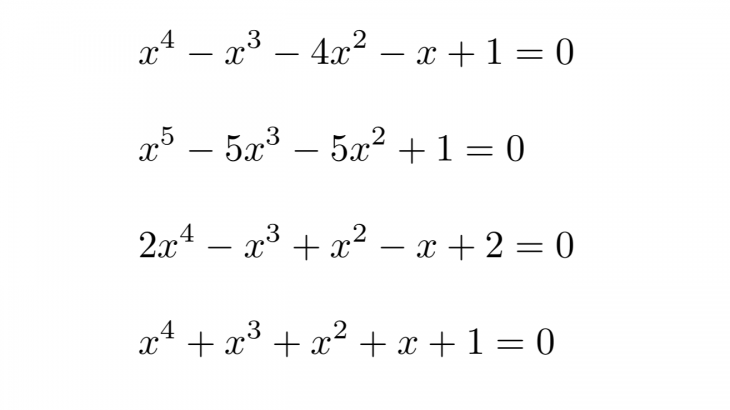この記事を読むとわかること
・相反方程式とはなにか
・相反方程式の解き方、その手法で解ける理由
・相反方程式の例題
・相反方程式に関わる応用問題
相反方程式とは
相反方程式とは係数が左右対称な方程式
相反方程式とは、降べきの順に並べたときに係数が左右対称になるような方程式のことを指します。例えば、
\[x^4+2x^3+3x^2+2x+1=0\]
は、係数が左から順に$1,\,2,\,3,\,2,\,1$と左右対称になっており、相反方程式になっていることがわかります。
相反方程式には決まった解き方がある
相反方程式には決まった解き方があり、実はたった2通りの解法を覚えるだけですべての問題に対応ができてしまいます。
この記事では、相反方程式の解き方を説明するとともに、なぜその解き方でうまくいくのかの理由や、相反方程式の考え方を応用した問題についても書いていきます!
相反方程式の解き方は?
相反方程式は、偶数次(2次方程式や4次方程式)か奇数次(3次方程式や5次方程式)かで解き方が変わります。
それぞれの場合について、例題を使って解き方を見ていきましょう!
偶数次の相反方程式の解き方
以下の4次相反方程式を例として解き方を説明していきます!
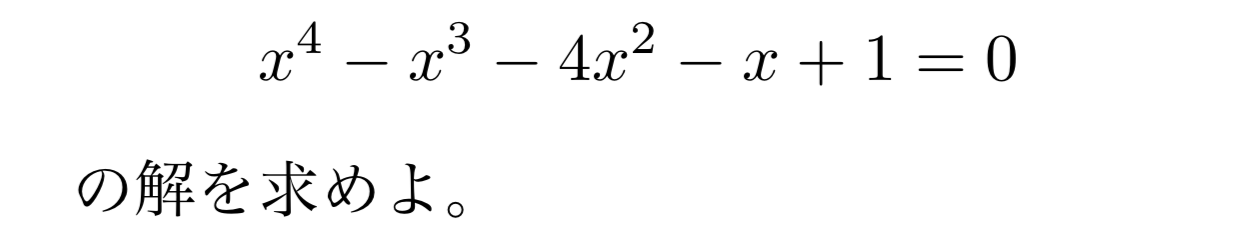
偶数次の相反方程式は3ステップで解くことができます!
偶数次($2n$次)の相反方程式の解き方
1. $x=0$が解でないことを確認してから$x^n$で割る
2.$X=x+\frac{1}{x}$とおいて$X$の方程式に帰着させる
3.$X$の解を求めて$x+\frac{1}{x}=(Xの解)$を解く
それぞれのステップについて詳しく見ていきましょう!
$x=0$が解でないことを確認してから$x^n$で割る
相反方程式を解く上で最も大事なステップは2番目の$X=x+\frac{1}{x}$とおいて$X$の方程式に帰着させることにあります。
そこで、まずはじめに$X$で表せる形にするために、偶数次の相反方程式は$2n$次であれば$x^n$で割るという操作を行います。
ここで注意したいのは$x^n$というのは$0$である可能性がある文字であるということです。数学では$0$で割るという操作を行っていないという鉄則がありますから、$x^n$で割る前に$x^n$が$0$ではないことをチェックしなければなりません。
これは、与えられた方程式に$x=0$を代入しても成立しないことを言えば簡単に示すことができますね。
上の例題について考えましょう。
$x=0$を代入すると$1=0$となってこれは成り立たないので、$x\ne0$のもとで考えることができて、4次の相反方程式なので、$x^2$で両辺を割って、
\[x^2-x-4-\frac{1}{x}+\frac{1}{x^2}=0\]
すればOKです。
$X=x+\frac{1}{x}$とおいて$X$の方程式に帰着させる
次は$x^n$で割ったあとの方程式を$X=x+\frac{1}{x}$の1文字だけで表すということをやります。この操作を行うことで、$2n$次の相反方程式は$X$の$n$次方程式に帰着させることができるので、方程式の次数を下げることができて方程式が解きやすくなるわけです。
例題について考えると、
\[\begin{align*}&x^2-x-4-\frac{1}{x}+\frac{1}{x^2}=0\\\Leftrightarrow &x^2+\frac{1}{x^2}-x-\frac{1}{x}-4=0\\\Leftrightarrow &\left(x+\frac{1}{x}\right)^2-2-\left(x+\frac{1}{x}\right)-4=0\\\Leftrightarrow &X^2-X-6=0\end{align*}\]
というように$X$の2次方程式に変換することができました!
どうして偶数次の相反方程式は$X=x+\frac{1}{x}$だけで表すことができるのでしょうか?これは、対称式の考え方を用いることで簡単に示せます。
文字を入れ替えても全く同じ意味になる式のことを対称式と呼びますが、対称式は基本対称式だけで表せるという有名な性質があります。
2文字の対称式において基本対称式とはその和と積、すなわち、$a+b$と$ab$です。2文字の対称式の例として$a^2+ab+b^2$などがありますが、これは実際$(a+b)^2-ab$というように基本対称式だけで表すことができます。
さて、偶数次の相反方程式を$x^n$で割ったあとは、$x$と$\frac{1}{x}$の対称式になっていると見ることができます。例題で言えば、
\[x^2-x-4-\frac{1}{x}+\frac{1}{x^2}\]
は、左半分の$x$を$\frac{1}{x}$に、右半分の$\frac{1}{x}$を$x$に変換すると、
\[\frac{1}{x^2}-\frac{1}{x}-4-x+x^2\]
となり、全く同じ意味の式になっていますよね。
よって、これらの和と積、つまり、$x+\frac{1}{x}(=X)$と$x\cdot\frac{1}{x}(=1)$だけで表すことができるので、結局$X$だけで表せるわけです。
$X$の解を求めて$x+\frac{1}{x}=(Xの解)$を解く
$X$の方程式に変換することができたらあとはそれを解いてから、$x+\frac{1}{x}$がその解になるという方程式を解くだけですね!
上の例題で言えば、
\[\begin{align*}X^2-X-6=0\Leftrightarrow &(X+2)(X-3)=0\\\Leftrightarrow &X=-2,\,3\end{align*}\]
となるので、
\[x+\frac{1}{x}=-2,\,x+\frac{1}{x}=3\]
の2つの方程式を解くだけです。$x\ne 0$であることに注意して、
\[x+\frac{1}{x}=-2\Leftrightarrow x^2+2x+1=0\Leftrightarrow x=-1\]
\[x+\frac{1}{x}=3\Leftrightarrow x^2-3x+1=0\Leftrightarrow x=\frac{3\pm\sqrt{5}}{2}\]
と解くことができるので、
\[\boldsymbol{x=-1,\,\frac{3\pm\sqrt{5}}{2}}\]
が答えになります。
奇数次の相反方程式の解き方
以下の5次相反方程式を例として解き方を説明していきます!
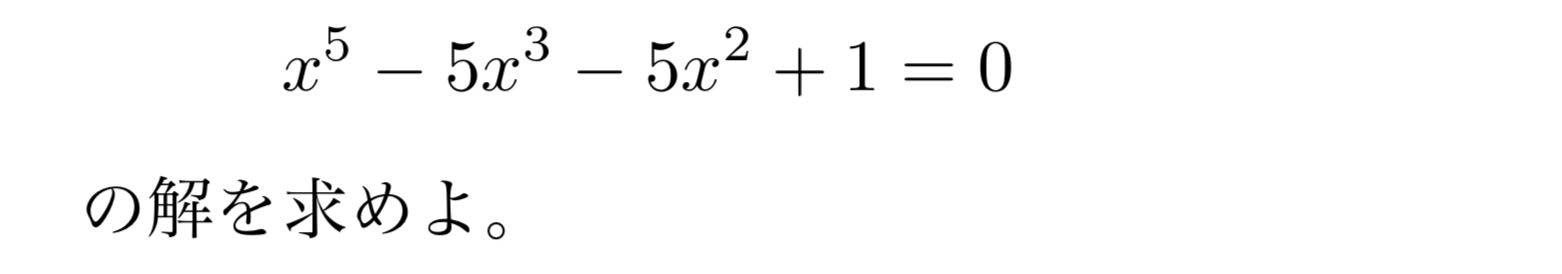
偶数次の相反方程式の解き方を覚えれば、奇数次の相反方程式の解き方を覚えるのは非常に簡単です!
奇数次の相反方程式の解き方
1.$(x+1)$でくくる
2.偶数次の相反方程式を解く
$(x+1)$でくくる
奇数次の相反方程式は必ず$x=-1$を解に持ちます。よって、まずは$x+1$でくくるという作業をすればOKです。
上の例題で言えば、$x=-1$を代入すると、
\[-1-5+5+1=0\]
となり、たしかに$-1$を解に持つことがわかりますね。
そこで、$(x+1)$でくくると、
\[\begin{align*}&x^5-3x^3-3x^2+1=0\\\Leftrightarrow &(x+1)(x^4-x^3-4x^2-x+1)=0\end{align*}\]
と変形することができます。
もう少し一般化して考えてみましょう。係数が左右対称な$2n+1$次式
は、
を満たすので、因数定理より$f(x)$は$x+1$で割り切れることがわかりますね。よって、奇数次の相反方程式が$x=-1$を常に解に持つことが簡単に言えます。
偶数次の相反方程式を解く
$x=-1$を解に持つことはすでにわかったので、$(x+1)$で割ったあとの方程式を解くことになります。
実は奇数次の相反方程式を$(x+1)$で割ると偶数次の相反方程式が出てきます。これは例題を見るとわかりやすいでしょう。$(x+1)$でくくったときの残りの部分を見てみると、
\[x^4-x^3-4x^2-x+1=0\]
となっており、偶数次の相反方程式になっていることがわかります!
そして、これは先ほど解いた例題と全く同じ方程式なので、同じ手順で解けることがわかります!
ちなみに、この知識を持っていれば、奇数次の相反方程式の左辺を$(x+1)$で割るときに、係数が左右対称になることがわかっていれば、割り算が楽になります。例題で言えば、割り算の商が$x^4-x^3-4x^2$まで求まれば$-x+1$の部分は対称性から即座にわかります。
奇数次の相反方程式を$(x+1)$で割ったときに係数が左右対称になるのはどうしてでしょうか?
これは以下のような流れで証明できそうです。
【証明】各項の係数が左右対称な$2n$次式
に$(x+1)$をかけると、
という各項の係数が左右対称な$2n+1$次式となる。これが
に等しくなるような$b_1,\,b_2,\,\cdots ,\,b_n,\,b_{n+1}$の存在を示せれば、$g(x)$が$f(x)$を$x+1$で割ったときの商となり、題意は示される。
つまり、連立方程式
\[\left\{\begin{array}{l}
b_1=a_1\\
b_1+b_2=a_2\\
b_2+b_3=a_3\\
\vdots\\
b_n+b_{n+1}=a_{n+1}
\end{array}\right.\]
の解が存在すればよい。1式目で$b_1$が定まり、それを2式目に代入すると$b_2$が定まる。それを3式目に代入して…と繰り返せば、添字の小さい順に値が定まる。
したがって、示された。
単に割り算をして商の係数が左右対称になってます、と言うよりもこちらの方が幾分か見やすい証明になっているかと思います。
相反方程式に関わる応用問題
「相反方程式を解け」という問題が入試で出ることはほとんどなく、上で紹介した解き方はあくまで係数が左右対称な多項式の扱いの一貫として知っておくべき基礎知識程度のものだと思った方がよいです。
そこで、相反方程式の知識を利用して解ける応用問題について2題紹介しようと思います!
応用問題1
解答・解説
$1$の$5$乗根というのは、
\[x^5=1\]
という方程式の解と言い換えることができます。これは、
\[x^5-1=0\Leftrightarrow (x-1)(x^4+x^3+x^2+x+1)=0\]
と変形できるので、$1$以外の5乗根は$x^4+x^3+x^2+x+1=0$という偶数次の相反方程式の解になっていることがわかりますね。
以下、解答例です。
求める値は、
\[x^5=1\]
の解である。この方程式は、
\[\begin{align*}&x^5-1=0\\\Leftrightarrow &(x-1)(x^4+x^3+x^2+x+1)=0\end{align*}\]
と変形できる。$x^4+x^3+x^2+x+1=0$について考える。$x=0$は解でないので、$x\ne0$としてよい。このもとで両辺を$x^2(\ne 0)$で割って、$X=x+\frac{1}{x}$とおくと、
\[\begin{align*}&x^2+x+1+\frac{1}{x}+\frac{1}{x^2}=0\\\Leftrightarrow &\left(x+\frac{1}{x}\right)^2+\left(x+\frac{1}{x}\right)-1=0\\\Leftrightarrow &X^2+X-1=0\\\Leftrightarrow &X=\frac{-1\pm\sqrt{5}}{2}\end{align*}\]
(i)$X=\frac{-1+\sqrt{5}}{2}$のとき、
$x\ne 0$に注意して、
\[\begin{align*}&x+\frac{1}{x}=0\frac{-1+\sqrt{5}}{2}\\\Leftrightarrow &2x^2+(1-\sqrt{5})x+2=0\\\Leftrightarrow &x=\frac{-1+\sqrt{5}\pm\sqrt{(1-\sqrt{5})^2-16}}{4}\\\Leftrightarrow &x=\frac{-1+\sqrt{5}\pm\sqrt{10+2\sqrt{5}}i}{4}\end{align*}\]
(i)$X=\frac{-1-\sqrt{5}}{2}$のとき、
$x\ne 0$に注意して、
\[\begin{align*}&x+\frac{1}{x}=0\frac{-1-\sqrt{5}}{2}\\\Leftrightarrow &2x^2+(1+\sqrt{5})x+2=0\\\Leftrightarrow &x=\frac{-1-\sqrt{5}\pm\sqrt{(1+\sqrt{5})^2-16}}{4}\\\Leftrightarrow &x=\frac{-1-\sqrt{5}\pm\sqrt{10-2\sqrt{5}}i}{4}\end{align*}\]
以上より、$1$の$5$乗根は、
数Ⅲをすでにやっている人であれば、ド・モアブルの定理を利用して、
\[x=\cos \frac{2k\pi}{5}+i\sin \frac{2k\pi}{5}(k=0,\,1,\,2,\,3,\,4)\]
になることが即座にわかりますが、$\frac{\pi}{5}$の余弦や正弦の値などを知らない人にとっては上の解法の方がはやく解けるかと思います。
応用問題2

解答・解説
4次関数が常に正の値を取ることを示す問題なので、パッと思いつくのは微分して増減表を描いて、という解法ではないでしょうか。しかし、微分したあとに出てくる3次式は綺麗に因数分解できない式になっているので、もう一度微分して常に正であることを示して…
というように、見かけによらずかなり議論が面倒になります。
しかし、係数が左右対称であることに注目すると、相反方程式を解くときに使った$X$の1文字だけで表すという手法が上手く使えます。$x=0$で成立することをチェックしてから、$x^2(>0)$で両辺を割ると$X$の2次不等式になります。
「文字の置き換えをしたらその変域を調べる」という鉄則に従うと、$X\leqq -2,\,2\leqq X$となっていることがわかるので、この範囲においてはたしかに2次不等式が成り立つことが言えます。
$X$の変域を求め忘れるとうまく証明できなくなってしまうので注意しましょう!
以下、解答例です。
$x=0$において与えられた不等式は成り立つので、以下$x\ne 0$の範囲について考える。両辺を$x^2(>0)$で割って、$X=x+\frac{1}{x}$と置き換えると、
\[\begin{align*}&2x^4-x^3+x^2-x+2>0\\\Leftrightarrow &2x^2-x+1-\frac{1}{x}+\frac{2}{x^2}>0\\\Leftrightarrow & 2\left(x+\frac{1}{x}\right)^2-\left(x+\frac{1}{x}\right)-3>0\\\Leftrightarrow &2X^2-X-3>0\end{align*}\]
となる。ここで、$X$の変域について考える。$X$の変域は、
\[X=x+\frac{1}{x}\Leftrightarrow x^2-Xx+1=0\]
が$x\ne 0$の範囲に実数解を持つ条件に等しいから、$x=0$が解でないことに注意すると、この方程式の判別式が$0$以上となる条件に等しい。したがって、
\[X^2-4\geqq 0\Leftrightarrow X\leqq -2,\,2\leqq X\]
よって、この範囲において、$2X^2-X-3>0$が成り立つことを示せればよい。
\[2X^2-X-3=(X+1)(2X-3)\]
となることに注意して、$X\leqq -2,\,2\leqq X$における$y=2X^2-X-3$のグラフを描くと以下のようになる。
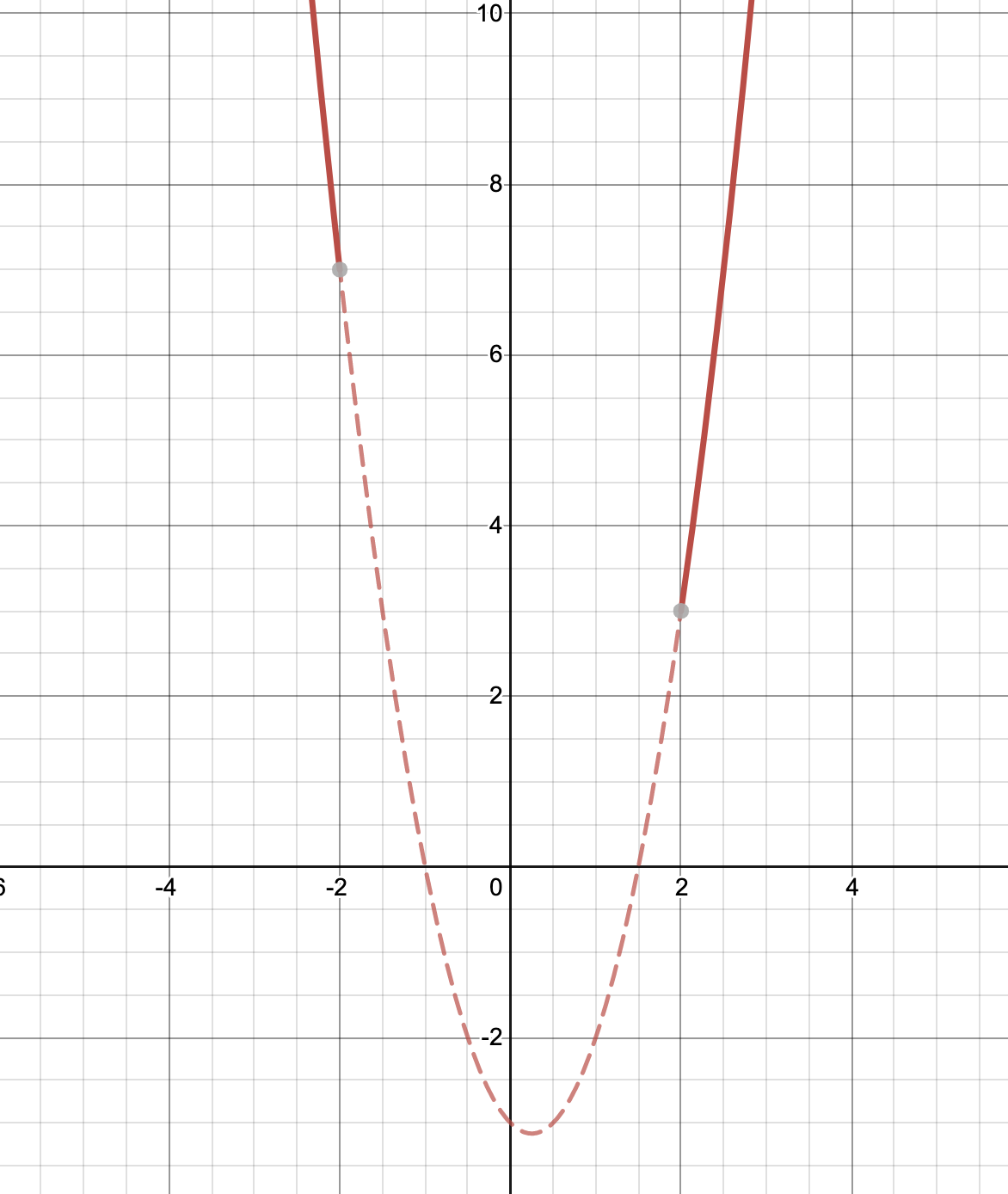
図より、たしかに$2X^2-X-3>0$が成り立っていることが分かるので題意成立。
上の解答例では$X$の変域を考える際には$x$の実数条件を考えることによって求めていますが、$x+\frac{1}{x}$を微分して値域を求めるという方法でも良いでしょう。
くれぐれも相加相乗平均の大小関係を用いた議論はしないようにしてください。有名不等式を用いると、最大値や最小値は求められても変域を求めたことにはならないですからね。
まとめ
・相反方程式とは係数が左右対称な方程式のこと
・偶数次の相反方程式は$X=x+\frac{1}{x}$で表すことによって扱う方程式の次数下げを行う
・偶数次の相反方程式は$x^n$で両辺を割った式が$x$と$\frac{1}{x}$の対称式になるので$X$だけで表せる
・奇数次の相反方程式は$x+1$で割り切れて残りは偶数次の相反方程式になる
・相反方程式そのものが入試で出ることはないがその考えを使うことは多い