東大医学部生の相談室

東大理系数学2020の入試問題・解答解説・難易度

東大理系数学2020の入試問題・解答解説・難易度

※以下の解答・解説は当ブログのオリジナルのものであり東京大学が公表しているものではありません。

私がおすすめする過去問題集について説明した記事はこちら↓

東大数学の過去問は鉄緑会が圧倒的におすすめ！その理由を東大医学部生が解説

目次

第一問

第一問は以下のような出題でした。

第一問の難易度分析

不等式に関する標準的な証明問題です。

「すべて」や「少なくとも1個」などの条件を示すときには、背理法を使うことが多いという点に気をつけていれば難なく完答できたでしょう。

第一問(1)を解く上での考え方・ポイント

「すべて〜である」ことを示すよりも、「どれか1つでも〜なものがあったら不都合が起こる」ことを示してあげる方が楽なことが多いです。

いわゆる背理法を利用するというわけですね。

「すべて〜」を示すときは背理法の利用を考える！

どれか1つでも負の数があると、2次の係数が負になっている不等式が出てきてしまいますが、このとき十分大きな$x$に対して絶対に不等式を満たさなくなってしまうので、$x>p$という集合と同じになるわけがないことが即座にわかります。

以下、解答例です。

$a,\,b,\,c$のうち少なくとも1つが負であると仮定する。このとき、対称性から$a$が負であるとして考えてよい。

このとき、十分大きな実数$x$に対して

\[ax^2+bx+c>0\]

は成立しない。よって、与えられた3つの不等式をすべて満たす実数$x$の集合が$x>p$を満たす実数$x$の集合と一致することはありえない。

したがって、元の仮定が誤りであり、$a,\,b,\,c$はすべて$0$以上。

第一問(2)を解く上での考え方・ポイント

「少なくとも1つ〜である」ことを示すよりも、「すべて〜でないときに不都合が起こる」ことを示してあげる方が楽なことが多いです。

(1)と同様に、いわゆる背理法を利用します。

「少なくとも1つ〜」を示すときは背理法の利用を考える！

すべて0でないときというのは、(1)の結果も踏まえるとすべてが正となっているときです。すべてが正であれば、3つの不等式をすべて満たすような実数$x$の集合は以下の図の赤線の部分のようになるはずです。

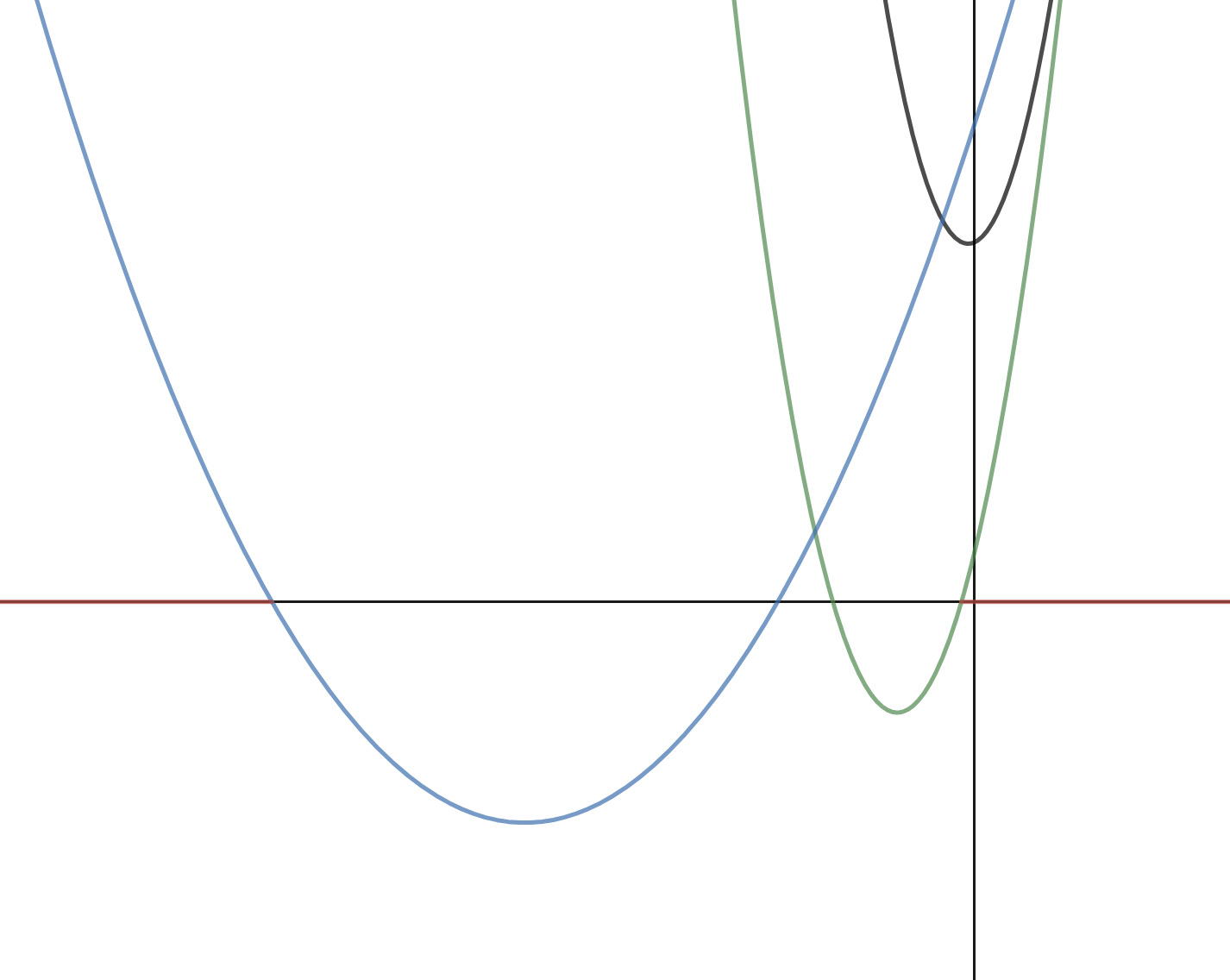
すなわち、$y=(与えられた不等式の左辺)$のグラフ3つと$x$軸との共有点が少なくとも1つあるならば、そのうち$x$座標が最も小さいものを$m$、最も大きいものを$M$としたときに、

\[x<m,\,M<x\]

となるはずだから、$x>p$とはなりえないだろうということがわかります。

さて、ここで問題になるのは、3つのグラフすべてが$x$軸と共有点を持たない可能性もあるということです。この場合分けが面倒なので、上手い議論のしかたを考えたいです。

 

結局のところ問題なのは$p$という下限が現れないという部分にあることに注目しましょう。すなわち、$a,\,b,\,c$がすべて正であるならば、十分小さな$x$に対してすべての不等式を満たすことになってしまうという議論に持っていくのがよいと思います。

以下、解答例です。

$a,\,b,\,c$がすべて$0$でないと仮定する。このとき、(1)より$a,\,b,\,c$はすべて正となる。ところがこのとき、十分小さな実数$x$に対して、与えられた3つの不等式はすべて成立してしまうので、これらをすべて満たす実数$x$の集合がすべて定数$p$よりも大きくなるということはありえない。

したがって、元の仮定が誤りであり、$a,\,b,\,c$のうち少なくとも1個は$0$。

第一問(3)を解く上での考え方・ポイント

(2)が示せたらあとは簡単です。対称性から、とりあえず$a=0$の時を考えてみて、実際に不等式を場合分けしつつ解いていくだけです！

以下、解答例です。

$a,\,b,\,c$は対称であるから、(2)より、$a=0$であるとして考えてよい。

$a=0$を与えられた不等式に代入すると、

\[\left\{\begin{array}{l}bx+c>0\\bx^2+cx>0\\cx^2+b>0\end{array}\right.\]

となる。

(i)$b>0$のとき、

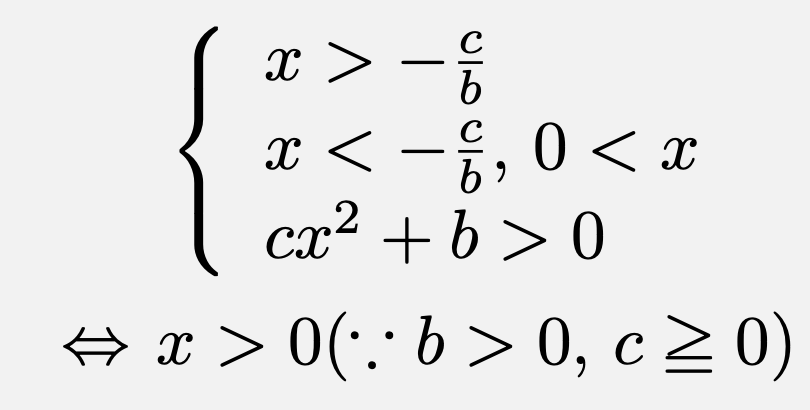
\begin{align*}&\left\{\begin{array}{l}x>-\frac{c}{b}\\x<-\frac{c}{b},\,0<x\\cx^2+b>0\end{array}\right.\\\Leftrightarrow &x>0(\because b>0,\,c\geqq 0)\end{align*}

となるので、$p=0$となる。

(ii)$b=0$のとき、

\[\left\{\begin{array}{l}c>0\\cx>0\\cx^2>0\end{array}\right.\]

となるので、$c=0$のときは与えられた不等式を満たす実数$x$が存在せず、$c>0$のときは、$x>0$となることが分かる。

 

以上より、$p=0$となることが示された。

第二問

第二問は以下のような出題でした。

第二問の難易度分析

易しい図形に関する問題です。

点Xと三角形ABCの位置関係には3つのパターンあることに気をつけて、それぞれの場合で条件式を満たすのがどのようなときかを丁寧に考えていけば簡単に解くことができます。

第二問を解く上での考え方・ポイント

点Xと三角形ABCの位置関係には以下の3つのパターンが考えられます。

 

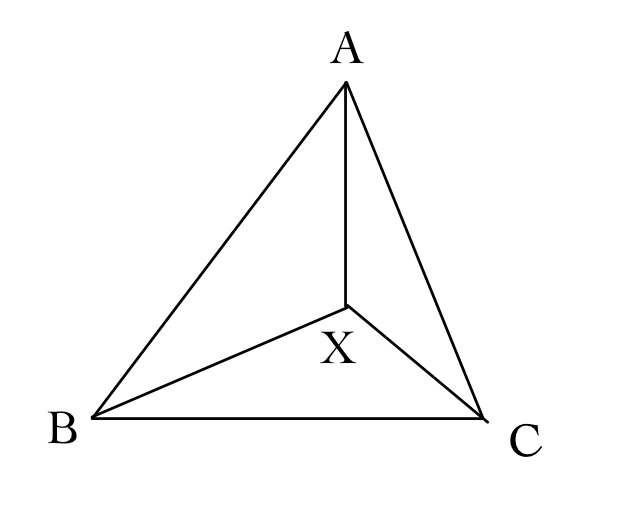
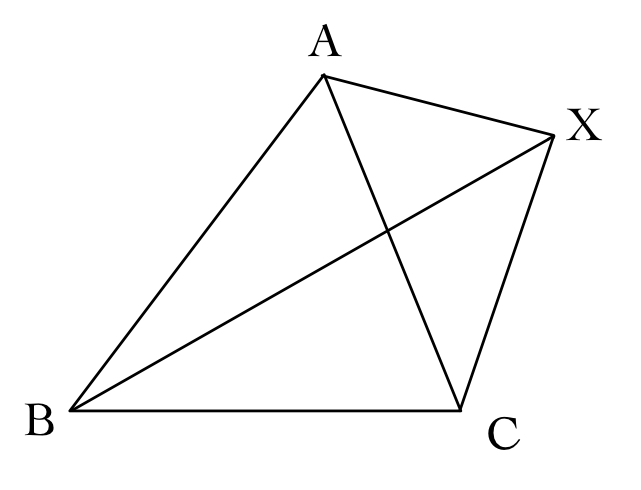
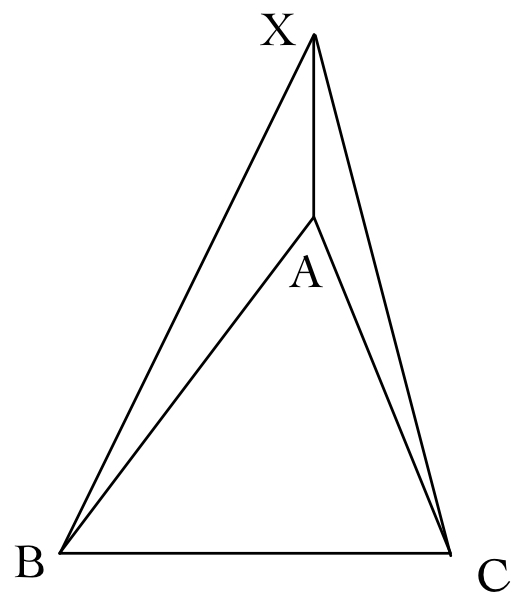
それぞれの場合において、満たすべき条件式を書き換えてあげると、点Xがどのような領域を動くか考えるのは難しくありません。

対称性を活かして、議論の繰り返しが起こらないように工夫しながら答案を書くとよいでしょう。

以下、解答例です。

(i)点Xが三角形ABCの内部および周上にあるとき、

\[\triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}=\triangle\mathrm{ABC}=1\]

より、与えられた条件を満たしえない。

(ii)線分BXが線分ACと共有点を持つ以下の図のようなとき、

\[\triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}=\triangle\mathrm{ABC}+2\triangle\mathrm{CAX}\]

である。

よって、点Xが満たす条件は、

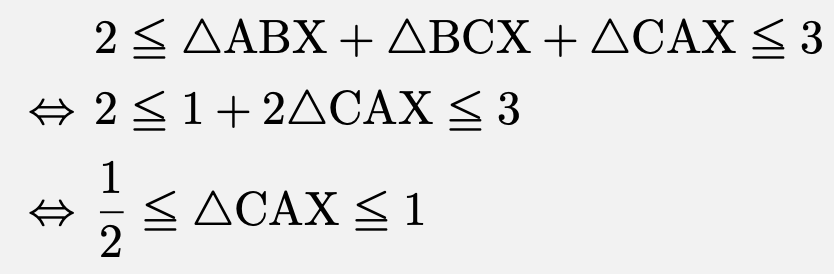
\begin{align*}&2\leqq \triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}\leqq 3\\\Leftrightarrow &2\leqq 1+2\triangle\mathrm{CAX}\leqq 3\\\Leftrightarrow &\frac{1}{2}\leqq\triangle\mathrm{CAX}\leqq 1\end{align*}

と書き換えることができる。したがって、点Xは下図の台形$\mathrm{PQRS}$の周上および内部を動く。

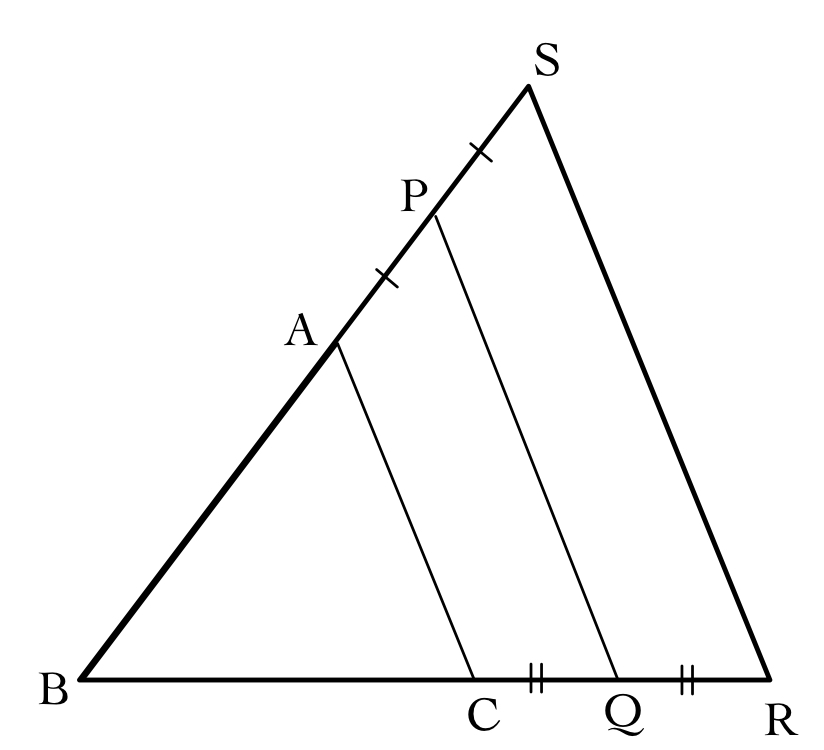
三角形$\mathrm{BRS}$の面積が三角形$\mathrm{ABC}$の面積の4倍であり、台形$\mathrm{PQRS}$の面積は三角形$\mathrm{BRS}$の$\frac{7}{16}$倍であることより、点Xが動く領域の面積は、

\[1\cdot 4\cdot \frac{7}{16}=\frac{7}{4}\]

となる。

 

対称性から、線分AXが線分BCと交わるとき、線分CXが線分ABと交わるときも同様に点Xの動く領域の面積は$\frac{7}{4}$となる。

(iii)線分AXを点A側に延長すると線分BCと交わる下図のようなとき、

\[\triangle\mathrm{ABX}+\triangle\mathrm{BCX}+\triangle\mathrm{CAX}=\triangle\mathrm{ABC}+2\triangle\mathrm{CAX}+2\triangle\mathrm{BAX}\]

よって、点Xが満たす条件は、

\[\frac{1}{2}\leqq \triangle\mathrm{CAX}+\triangle\mathrm{BAX}\leqq 1\]

ここで、線分XAを点A側に延長したときに線分BCと交わる点をDとすると、この条件を満たすのは、$\mathrm{XA}:\mathrm{AD}=r:1(\frac{1}{2}\leqq r\leqq 1)$となるとき。

よって、点Xは下図の台形EFGHの内部および周上を動く。

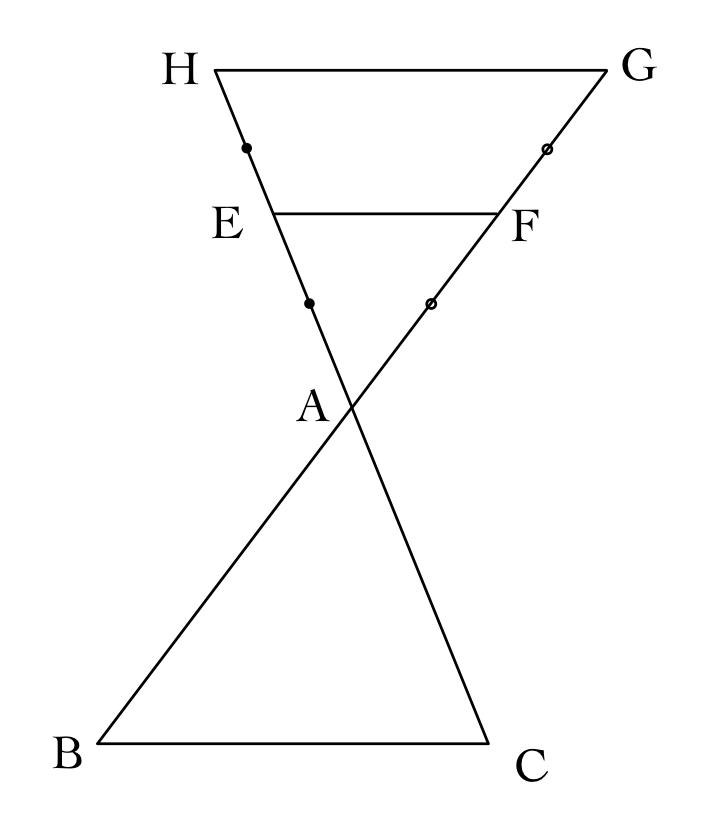
この面積は、三角形ABCの面積の$\frac{3}{4}$倍であるので、

 

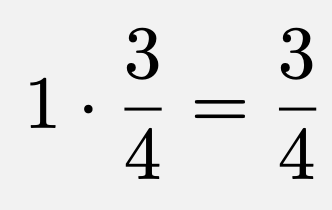
ここで、対称性から、線分XBを点B側に延長したときに線分CAと交わるとき、線分XCを点C側に延長したときに線分ABと交わるときも同様に点Xの動く領域の面積は$\frac{3}{4}$となる。

 

以上より、求める面積は、それぞれの領域がその周以外で互いに重なることがないことに注意して、

\[\frac{7}{4}\cdot 3+\frac{3}{4}\cdot 3=\boldsymbol{\frac{15}{2}}\]

第三問

第三問は以下のような出題でした。

第三問の難易度分析

微分積分に関する標準的な問題です。

(3)における軌跡$C$についての必要な情報を(1)と(2)で求めさせる丁寧な誘導がついており、計算量は少し多めですが完答するのは難しくないでしょう。

第三問(1)を解く上での考え方・ポイント

ただの微分の問題です。分母の$x(t)$は$t=-1$のときに0になってしまうので、この問題では$-1<t\leqq 1$の範囲で議論するようになっています。

以下、解答例です。

\[\frac{y(t)}{x(t)}=\frac{3\sqrt{1-t}}{\sqrt{1+t}}\]

$-1< t< 1$の範囲において、これを$t$で微分すると、

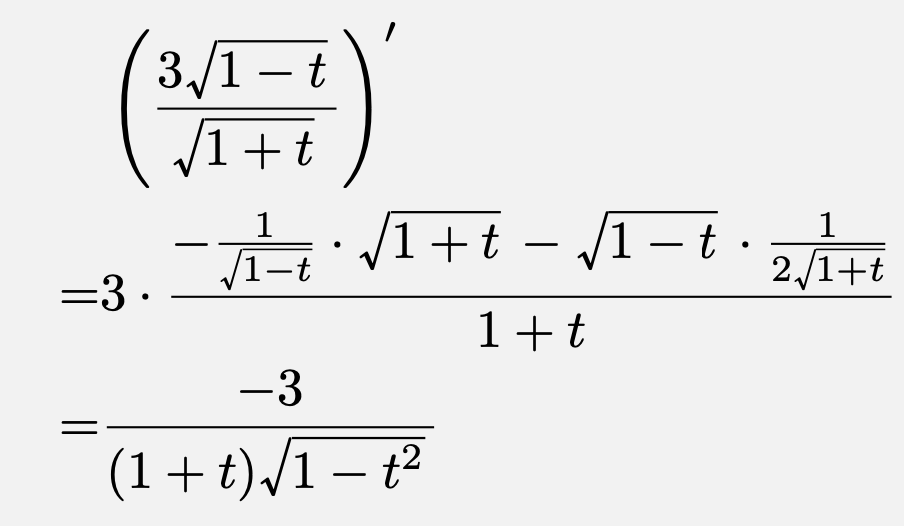
\begin{align*}&\left(\frac{3\sqrt{1-t}}{\sqrt{1+t}}\right)'\\=&3\cdot\frac{-\frac{1}{\sqrt{1-t}}\cdot\sqrt{1+t}-\sqrt{1-t}\cdot\frac{1}{2\sqrt{1+t}}}{1+t}\\=&\frac{-3}{(1+t)\sqrt{1-t^2}}\end{align*}

これは$-1< t< 1$の範囲で常に負であるので、$\frac{y(t)}{x(t)}$は単調に減少することが示された。

$t=1$のときは微分係数が定義できませんが、$t=1$において連続であることも考えると、上の議論で単調に減少することは言ってしまってよいですね。

第三問(2)を解く上での考え方・ポイント

原点と点Pとの間の距離を表す$f(t)$を求めてあげてからまた微分するだけです。$\sqrt{2(1+t)^2(5-4t)}$が最大になるときを求めることになりますが、このままの形で微分しないように気をつけましょう。

$-1\leqq t\leqq 1$において、ルートの中身は常に正になっているので、距離が最大になるときとルートの中身が最大になるときは等しいです。よって、ルートの中身である3次関数の微分をしてあげれば十分であり、ルートの微分をする必要性はありません。

以下、解答例です。

\[f(t)=\sqrt{\{x(t)\}^2+\{y(t)\}^2}=\sqrt{2(1+t)^2(5-4t)}\]

$-1\leqq t\leqq 1$において常に$2(1+t)^2(5-4t)>0$であることより$f(t)$が最大になるときと$2(1+t)^2(5-4t)$が最大になるときは等しい。

\[g(t)=2(1+t)^2(5-4t)\]

とおくと、

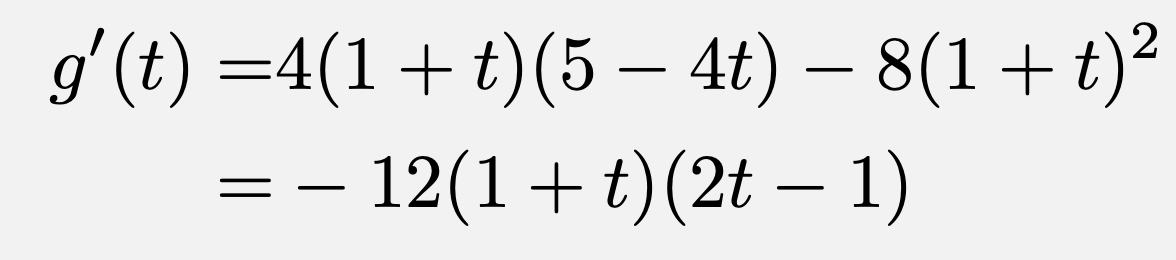
\begin{align*}g'(t)=&4(1+t)(5-4t)-8(1+t)^2\\=&-12(1+t)(2t-1)\end{align*}

よって、増減表は以下のようになる。

\[\begin{array}{|c||c|c|c|c|c|} \hline t&-1&\cdots&\frac{1}{2}&\cdots&1\\\hline g'(x)&&+&&-&\\\hline g(x)&0&\nearrow&\frac{27}{2}&\searrow&8\\\hline\end{array}\]

したがって、求める最大値は、

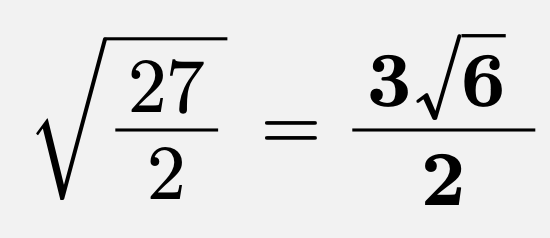
第三問(3)を解く上での考え方・ポイント

あとは積分計算をするだけなので、難しくありません。(1)と(2)から、下図のような図が描けて、求めるべき面積は、オレンジ色の扇形の面積と、赤色の図形のうち扇形の外側にある部分と青色の図形のうち扇形の外側にある部分の面積の和(これは赤色の図形1個の面積と等しい)の合計です。

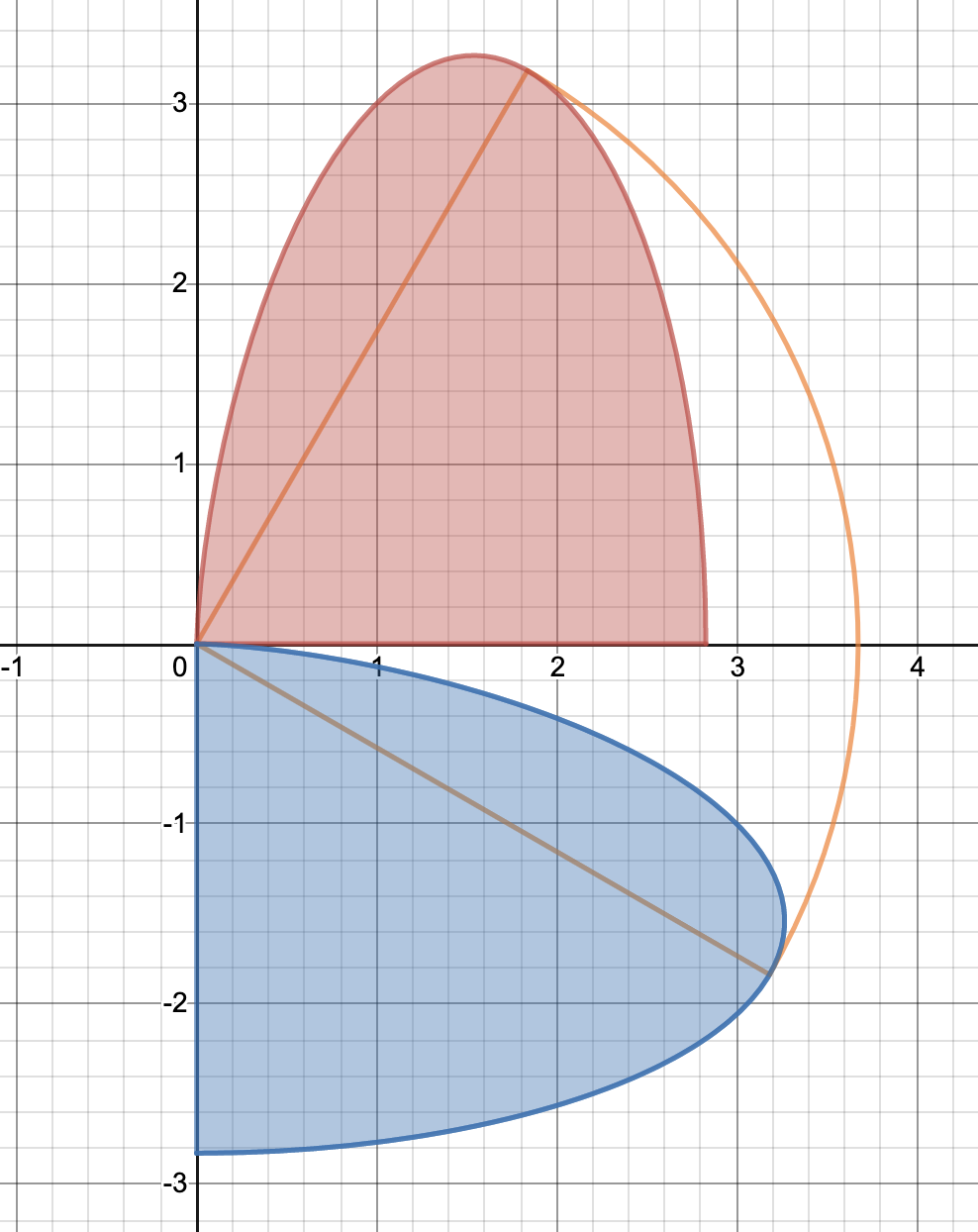
したがって、扇形の面積を計算することと、$D$の面積を計算してあげればOKです。

以下解答例です。

(1)、(2)より、$D$を$90^{\circ}$回転させると上図のようになるので、求めるべき面積は、$D$の面積と、半径$\frac{3\sqrt{6}}{2}$で中心角$\frac{\pi}{2}$の扇形の面積の和である。

$D$の面積は、$x(t)$が$t$についての単調増加な関数であることに注意すると、

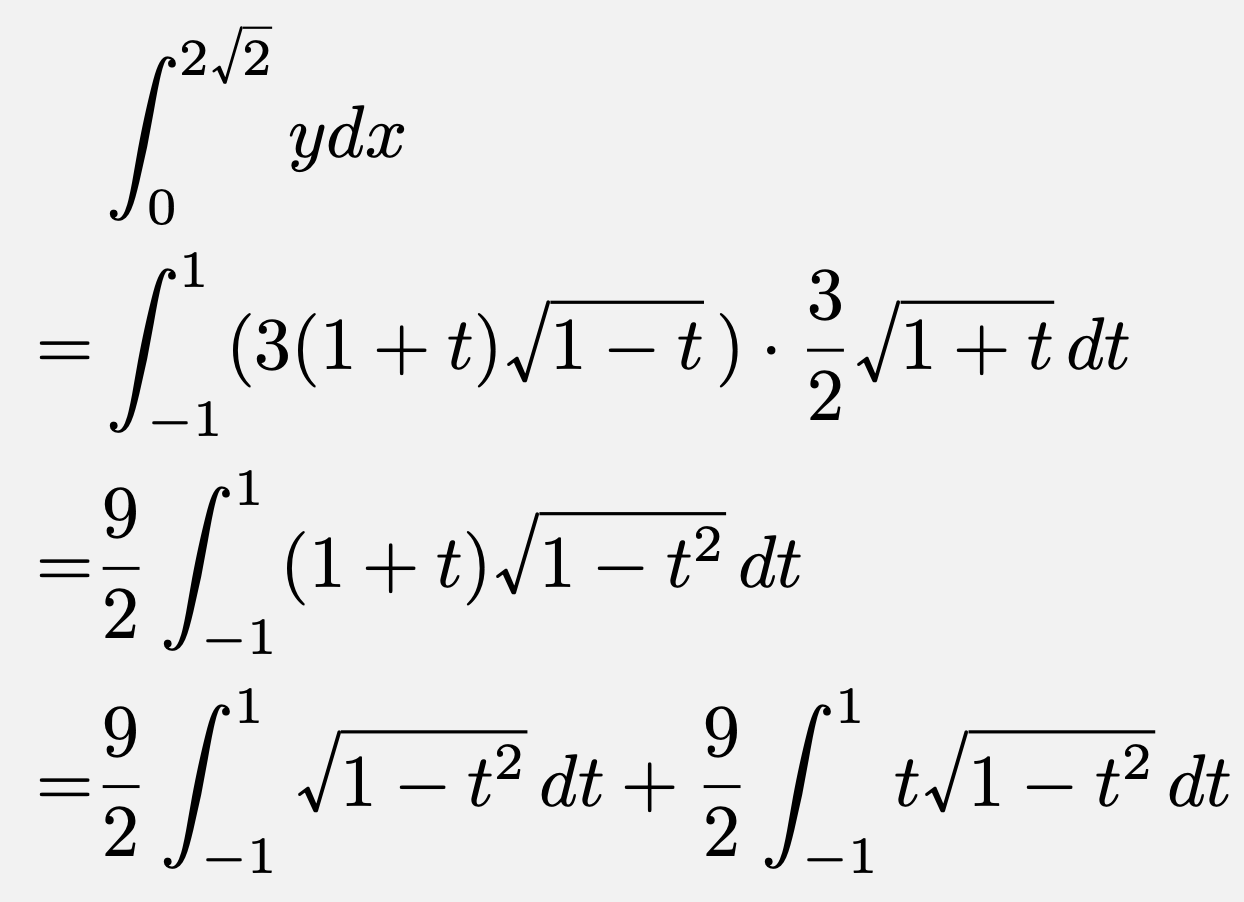
\begin{align*}&\int_{0}^{2\sqrt{2}}ydx\\=&\int_{-1}^{1}(3(1+t)\sqrt{1-t})\cdot \frac{3}{2}\sqrt{1+t}dt\\=&\frac{9}{2}\int_{-1}^{1}(1+t)\sqrt{1-t^2}dt\\=&\frac{9}{2}\int_{-1}^{1}\sqrt{1-t^2}dt+\frac{9}{2}\int_{-1}^{1}t\sqrt{1-t^2}dt\end{align*}

ここで、$t\sqrt{1-t^2}$は奇関数であるから、

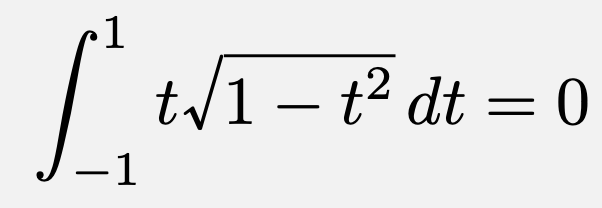
であり、$\int_{-1}^{1}\sqrt{1-t^2}dt$は半径1の半円の面積に等しいので、

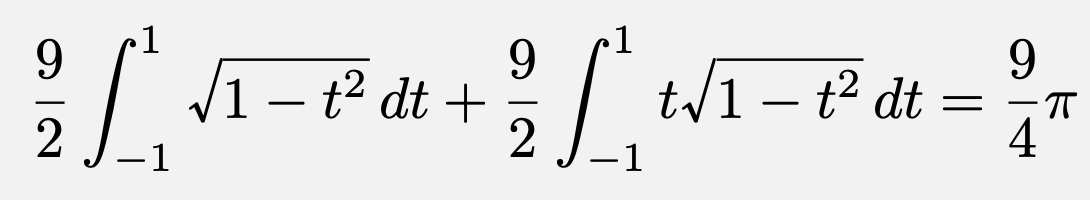
また、半径$\frac{3\sqrt{6}}{2}$で中心角$\frac{\pi}{2}$の扇形の面積は$\frac{27}{8}\pi$であるから、求める面積は、

\[\frac{9}{4}\pi+\frac{27}{8}\pi=\boldsymbol{\frac{45}{8}\pi}\]

第四問

第四問は以下のような出題でした。

第四問の難易度分析

やや難しい組み合わせや整数についての問題です。

(2)において、$a_{n+1,\,k+1}$を$a_{n,\,k}$を用いて表すやり方を2種類思い付けるかどうかが完答できるかどうかの分かれ目になったと思われます。(2)ができれば(3)はボーナス問題です。

第四問(1)を解く上での考え方・ポイント

異なる2つを選んでかけ合わせたものの総和を求めればよいのですが、これはやったことのある受験生も多いのではないかと思います。

\[(2^0+2^1+\cdots +2^{n-1})^2\]

を展開してあげると、同じものをかけ合わせたもの(つまりそれぞれの要素の平方)と、異なる2つをかけ合わせたものが2セット出てきます。よって、平方の和を除いてあげてから$\frac{1}{2}$倍してあげれば求めたいものが得られますね。

以下、解答例です。

\[a_{n,\,2}=\frac{1}{2}\left\{\left(\sum_{k=0}^{n-1}2^k\right)^2-\sum_{k=0}^{n-1}2^{2k}\right\}\]

であり、

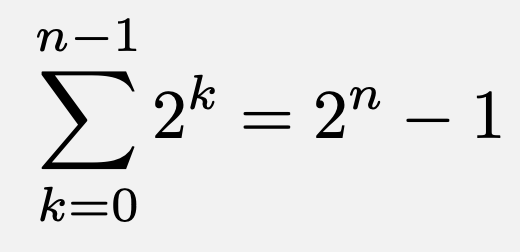
\[\sum_{k=0}^{n-1}2^{2k}=\frac{4^n-1}{4-1}=\frac{4^n-1}{3}\]

であるから、

\[a_{n,\,2}=\frac{1}{2}\left\{(2^n-1)^2-\frac{4^n-1}{3}\right\}=\boldsymbol{\frac{4^n}{3}-2^n+\frac{2}{3}}\]

第四問(2)を解く上での考え方・ポイント

求めるべき式は$\frac{(n+1次式)}{(n次式)}$となっているので、求めるべき整式は1次式になっているはずです。

よって、最高次の係数と定数項に着目すれば、$\frac{f_{n+1}(x)}{f_{n}(x)}=\frac{a_{n+1,\,n+1}}{a_{n,\,n}}x+1=2^nx+1$、$\frac{f_{n+1}(x)}{f_{n}(2x)}=\frac{a_{n+1,\,n+1}}{2^n\cdot a_{n,\,n}}+1=x+1$となることはすぐに分かってしまいますね。

ただ、本当に割り切れるかどうかまで議論しなければ解答にはならないので、$a_{n+1,\,k+1}$を$a_{n,\,k}$で表すことを試みます。この表し方が2通り考えられるというのがこの問題の肝になってきます。

以下、解答例です。

$1\leqq k\leqq n-1$の範囲において、$a_{n+1,\,k+1}$について、$2^n$を選ぶときは、残りの$n$個の中から$k$個を選ぶことになり、$2^n$を選ばないときは、残りの$n$個の中から$k+1$個を選ぶことになる。これらは排反なので、

\[a_{n+1,\,k+1}=2^na_{n,\,k}+a_{n,\,k+1}\]

が言える。これを用いると、

\[f_{n+1}(x)=1+(2^n+a_{n,\,1})x+(2^na_{n,\,1}+a_{n,\,2})x^2+\cdots+2^na_{n,\,n}x^n\]

となるので、

\[f_{n+1}(x)=(2^nx+1)f_n(x)\]

が言える。よって、

 

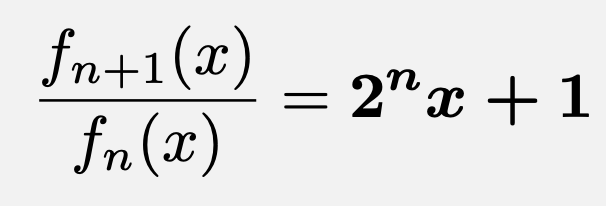
また、$1\leqq k\leqq n-1$の範囲において、$a_{n+1,\,k+1}$について、$2^0$を選ぶときは、残りの$n$個の中から$k$個を選ぶことになり、$2^0$を選ばないときは、残りの$n$個の中から$k+1$個を選ぶことになる。これらは排反なので、

が言える。これを用いると、

\[f_{n+1}(x)=1+(1+2^1a_{n,\,1})x+(2^1a_{n,\,1}+2^2a_{n,\,2})x^2+\cdots+2^na_{n,\,n}x^n\]

となるので、

\[f_n(2x)=1+2^1a_{n,\,1}x+2^2a_{n,\,2}+\cdots+2^na_{n,\,n}\]

であることから、

\[f_{n+1}(x)=(x+1)f_n(2x)\]

が言える。よって、

\[\frac{f_{n+1}(x)}{f_n(2x)}=\boldsymbol{x+1}\]

第四問(3)を解く上での考え方・ポイント

(2)が良い誘導になっています。$a_{n+1,\,k+1}$と$a_{n,\,k}$を結ぶ式を2種類立てたので、これを連立して不要な$a_{n,\,k+1}$を消してやれば求めたい式が得られます。

ただし、(2)で導いた式は$1\leqq k\leqq n-1$の範囲でしか成り立たないことに注意しましょう。$k=n$のときは分けて議論する必要があります。

以下、解答例です。

(2)より、$1\leqq k\leqq n-1$の範囲において、

\[a_{n+1,\,k+1}=2^na_{n,\,k}+a_{n,\,k+1}=2^ka_{n,\,k}+2^{k+1}a_{n,\,k+1}\]

が成り立つ。ここから、$a_{n,\,k+1}$を消去して、

\[(2^{k+1}-1)a_{n+1,\,k+1}=(2^{n+k+1}-2^k)a_{n,\,k}\]

\[\therefore \frac{a_{n+1,\,k+1}}{a_{n,\,k}}=\frac{2^k(2^{n+1}-1)}{2^{k+1}-1}\]

これは、$k=n$のときも成り立つ。したがって、

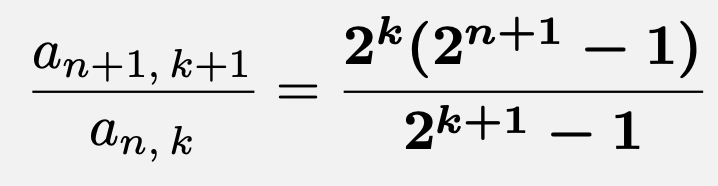
第五問

第五問は以下のような出題でした。

第五問の難易度分析

易しい立体図形の求積問題です。

立体図形の求積問題は適切な切断面を考えることが重要です。今回は(1)で切断面を考えさせる誘導がついているのでかなり取り組みやすくなっていますね。

第五問(1)を解く上での考え方・ポイント

$t$を$z=1$で切断すると線分APの中点の集まりが出てきますね。中点の座標を計算したいので、点Pの座標を$(\cos \theta,\,\sin\theta,\,0)(0\leqq \theta<2\pi)$のように書き表すのがよいでしょう。

以下、解答例です。

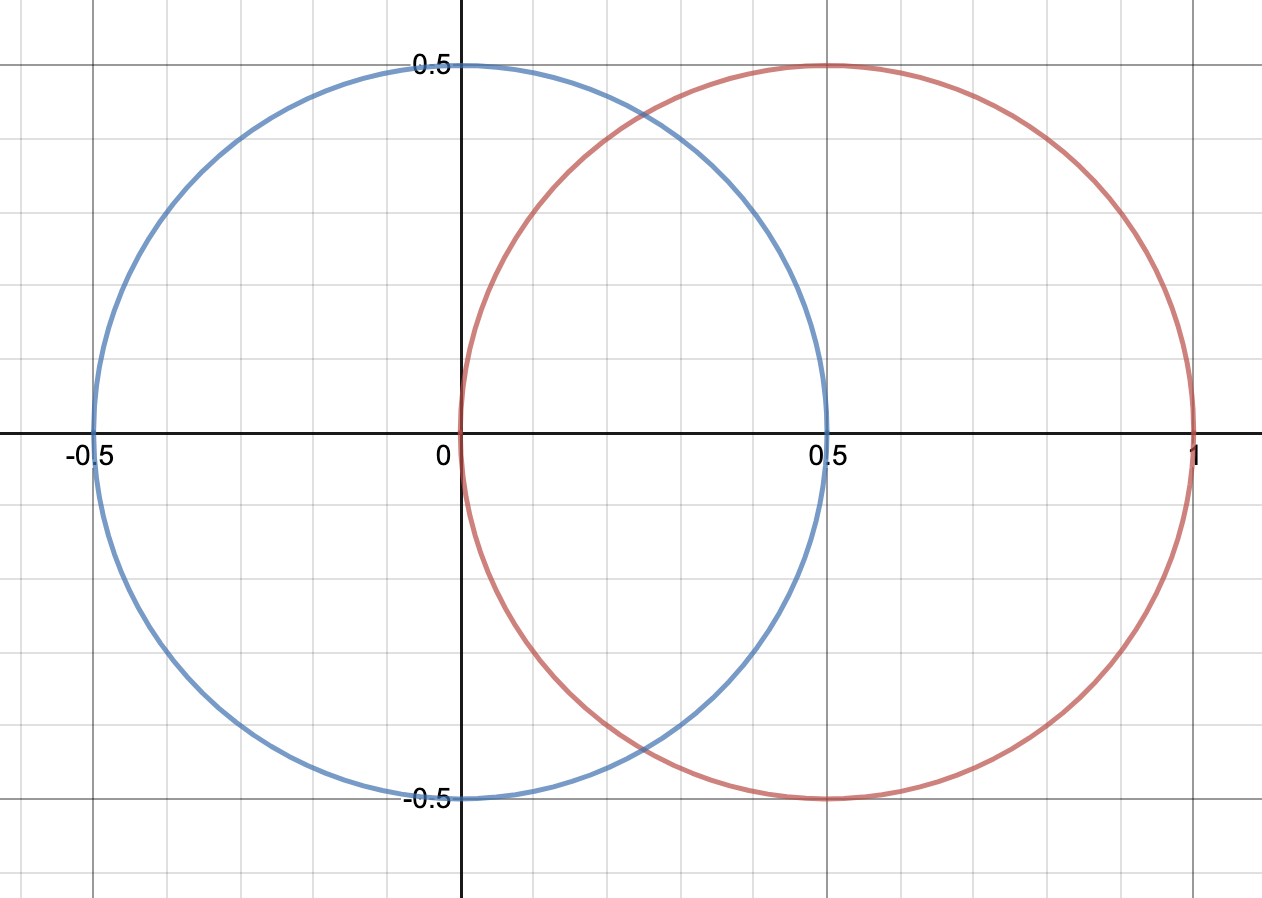
点Pの座標は$(\cos \theta,\,\sin\theta,\,0)(0\leqq \theta<2\pi)$のように書ける。線分APの中点をMとすると、

\[\mathrm{M}\left(\frac{1}{2}+\frac{1}{2}\cos\theta,\,\frac{1}{2}\sin\theta,\,1\right)\]

となるので、点Mは$(\frac{1}{2},\,0,\,1)$を中心とする、半径$\frac{1}{2}$の円周上を動く。

また、円錐の頂点$(0,\,0,\,2)$をBと名付け、線分BPの中点をNとする。同様にして、

\[\mathrm{N}\left(\frac{1}{2}\cos\theta,\,\frac{1}{2}\sin\theta,\,1\right)\]

となるので、点Nは$(0,\,0,\,1)$を中心とする、半径$\frac{1}{2}$の円周上を動く。

したがって、切り口を同一平面上に図示すると以下のようになる。

第五問(2)を解く上での考え方・ポイント

(1)が誘導になっています。

点Pの$z$座標が固定されている状態であれば、高さによらず同じ半径の円が切り口として出てくることが(1)の結果から想像できます。よって、切り口として出てくる円の中心がどの範囲を動くか考えるのが大事で、これは、Tの切断面の中心とSの切断面の中心を結んだ線分となることがわかります。

結局の所、円が動いてできる面積を$z$軸方向に積分して体積を求めるだけの作業です。

以下、解答例です。

$z=t(0\leqq t\leqq 2)$で切断して考える。点Pが$z=k$上にあるときを考えると、線分APが$z=t$と交点を持つのは、$0\leqq k\leqq t$を満たすときだけである。

点Pが$z=k$上にあるとき、点Pの座標は$(r\cos \theta,\,r\sin\theta,\,0)(0\leqq \theta<2\pi,\,0\leqq r\leqq \frac{2-k}{2})$と表すことができて、このとき、線分APと$z=t$との共有点は、

\[\left(\frac{2-t}{2-k}r\cos \theta+\frac{t-k}{2-k},\,\frac{2-t}{2-k}r\sin\theta,\,t\right)\]

となる。よって、これが動く範囲は、点$\left(\frac{t-k}{2-k},\,0\right)$を中心とする半径$\frac{2-t}{2}$の円板。$k$を$0\leqq k\leqq t$の範囲で動かすと、円の中心は長さ$\frac{t}{2}$の線分上を動くことになり、求める図形の断面図は下図のような領域となる。

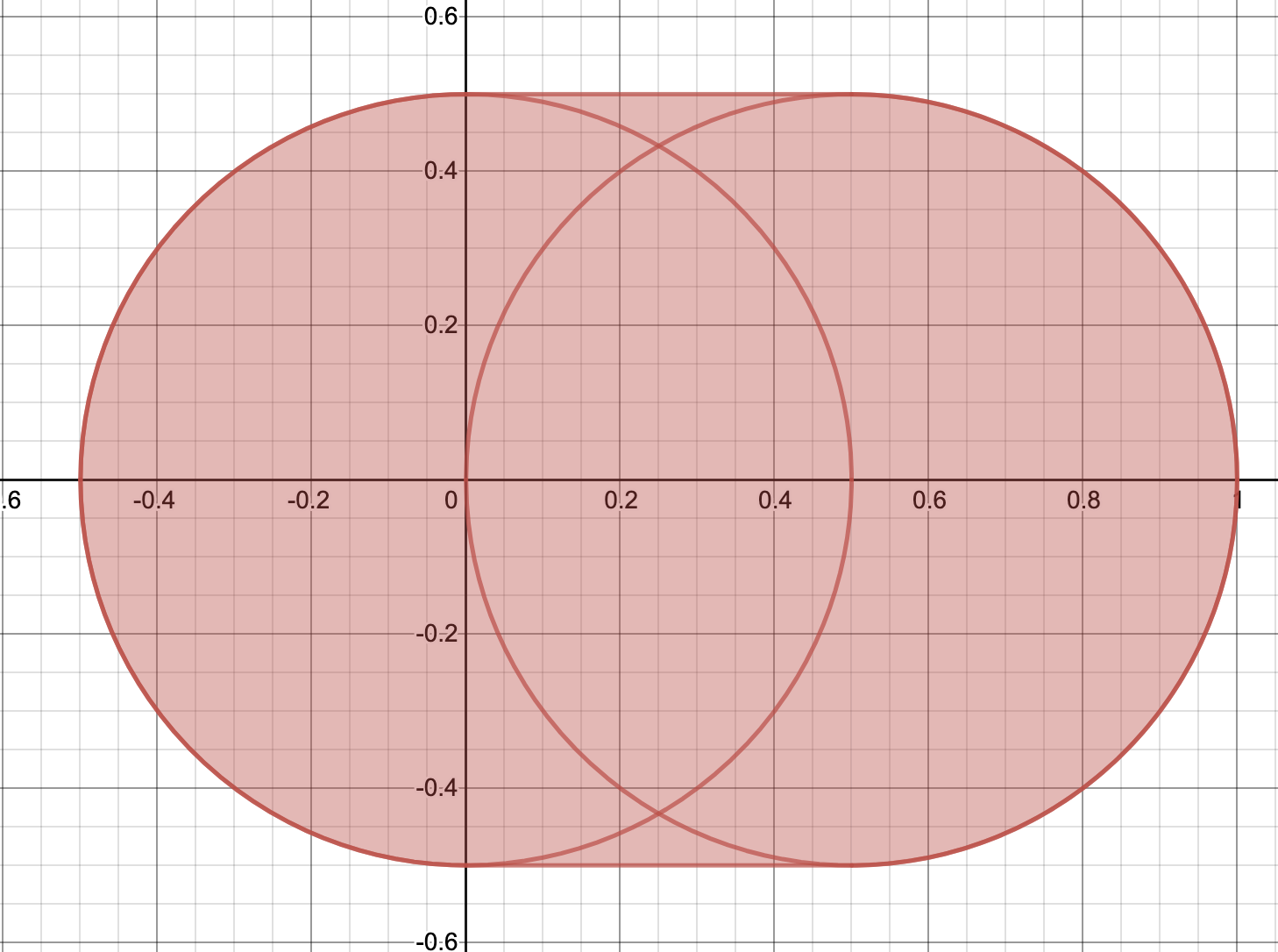
したがって、求める体積は、

\begin{align*}&\int_{0}^{2}\left\{\left(\frac{2-t}{2}\right)^2\pi+\frac{t}{2}(2-t)\right\}dt\\=&\left[\frac{\pi(t-2)^3}{12}\right]_{0}^{2}+\frac{1}{12}(2-0)^2\\=&\boldsymbol{\frac{2}{3}(\pi+1)}\end{align*}

第六問

第六問は以下のような出題でした。

第六問の難易度分析

やや難しい2次曲線に関する問題です。

(1)の「少なくとも4個の解を持つ」と(2)の「少なくとも4個ある」がどうつながるのかを意識しながら解いていくことが重要です。(1)の証明問題はかなりシンプルなのですが、難しく考えてしまって混乱してしまった受験生も多いかと思います。

第六問(1)を解く上での考え方・ポイント

$A>1$という条件は何かというと、「$\sin(\theta+\alpha)$がどんな値を取ろうが、$\sin\2\theta$が最大値になれば正になるし、最小値になれば負になる」ための条件です。

これを踏まえると、中間値の定理を用いて、解の存在を示すことができます。

以下、解答例です。

与えられた$\theta$の方程式の左辺を$f(\theta)$とおくと、$A>1$のとき、

\[f\left(\frac{\pi}{4}\right)=A-\sin(\theta+\alpha)>0\]

\[f\left(\frac{3\pi}{4}\right)=-A-\sin(\theta+\alpha)<0\]

\[f\left(\frac{5\pi}{4}\right)=A-\sin(\theta+\alpha)>0\]

\[f\left(\frac{7\pi}{4}\right)=-A-\sin(\theta+\alpha)<0\]

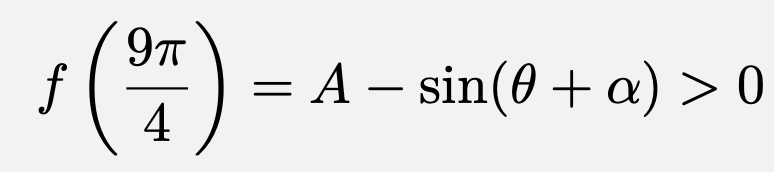
が成り立つので、中間値の定理から$\frac{\pi}{4}<\theta<\frac{3\pi}{4}$、$\frac{3\pi}{4}<\theta<\frac{5\pi}{4}$、$\frac{5\pi}{4}<\theta<\frac{7\pi}{4}$、$\frac{7\pi}{4}<\theta<\frac{9\pi}{4}$の範囲に少なくとも1つずつ実数解を持つことが言える。

$\frac{7\pi}{4}<\theta<\frac{9\pi}{4}$の範囲にある解については、$2\pi\leqq \theta<\frac{9\pi}{4}$を満たす解しか存在しないとき、その$\theta$から$2\pi$を引いた値も解になるので、$0\leqq \theta<\frac{\pi}{4}$の範囲に実数解を持つことになる。

したがって、$0\leqq \theta<2\pi$の範囲に少なくとも4個の解を持つことが示された。

第六問(2)を解く上での考え方・ポイント

問題文の条件が理解しにくく、かなり難しい問題だと思います。

問題文を言い換えると、「楕円$C$上を点Qが1周動くときに、点Qにおける法線がある点$(x,\,y)$を通るというのが、$2x^2+y^2<r^2$という領域内の点ならば少なくとも4回以上起こる」という感じです。

そこで、とりあえず法線の式を立ててみて、どうにか(1)で出てきた式につながらないかな〜と考えながら変形を進めていきます。

点Qの座標は$(\sqrt{2}\cos\theta,\,\sin\theta)$と表すことができる。接線の法線ベクトルの1つに$(\frac{1}{\sqrt{2}}\cos\theta,\,\sin\theta)$があるので、点Qを通る楕円$C$に対する法線の方程式は、

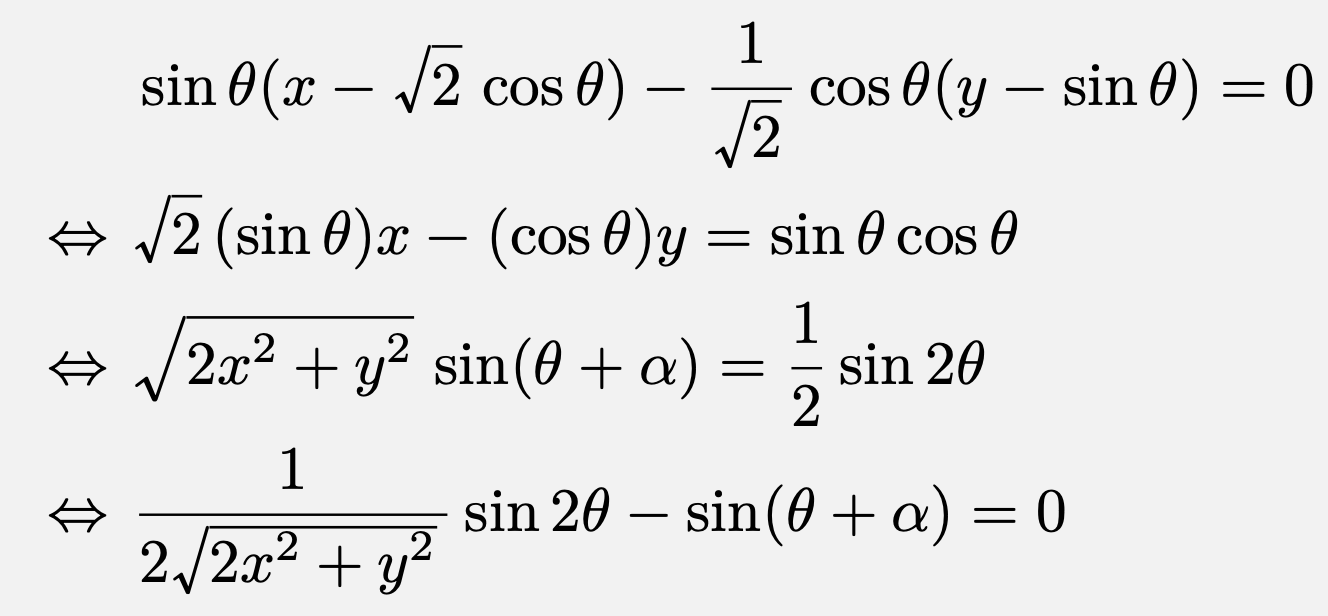
\begin{align*}&\sin\theta (x-\sqrt{2}\cos\theta)-\frac{1}{\sqrt{2}}\cos\theta(y-\sin\theta)=0\\\Leftrightarrow &\sqrt{2}(\sin\theta) x-(\cos\theta)y=\sin\theta\cos\theta\\\Leftrightarrow &\sqrt{2x^2+y^2}\sin(\theta+\alpha)=\frac{1}{2}\sin2\theta\\\Leftrightarrow &\frac{1}{2\sqrt{2x^2+y^2}}\sin2\theta-\sin(\theta+\alpha)=0\end{align*}

ただし、$\alpha$は、$0\leqq \alpha<2\pi$、$\cos\alpha=\frac{\sqrt{2}x}{\sqrt{2x^2+y^2}}$、$\sin\alpha=\frac{-y}{\sqrt{2x^2+y^2}}$を満たす実数。

法線の式を立てて合成を行うと(1)の式や$2x^2+y^2$の形が出てきました！(1)の結果から、$\frac{1}{2\sqrt{2x^2+y^2}}>1$すなわち$0\geqq 2x^2+y^2<\frac{1}{4}$を満たしているときにはこの方程式を満たすような$\theta$が少なくとも4個あるので、OKです。

これでとりあえず題意を満たすような$r$が存在することは示せます。

(1)の結果より、

\[\frac{1}{2\sqrt{2x^2+y^2}}>1\Leftrightarrow 0< 2x^2+y^2<\frac{1}{4}\]

を満たす点$(x,\,y)$は$\theta$の解を少なくとも4個持つので、$0<r\leqq \frac{1}{2}$の範囲にある実数$r$は条件を満たす。よって、題意を満たす$r$が存在することは示された。

最後に$r$の最大値を考えなければなりませんが、$0<r\leqq \frac{1}{2}$ならOKという情報が突然無駄になるはずもないので、「どうせ最大値は$\frac{1}{2}$になるんだろう」と考えるのが自然です。

よって、$r>\frac{1}{2}$となったとき、すなわち、点Pが$2x^2+y^2=\frac{1}{4}$上にあることを許したときに何か不都合が生じることを言えれば良さそうですね。

さて、生じる不都合というのはもちろん、$2x^2+y^2=\frac{1}{4}$を代入したときに出てくる、

\[\sin2\theta -\sin\left(\theta+\alpha\right)=0\]

という方程式が$0\leqq \theta<2\pi$の範囲に4個以上の解を持たなくなることであるわけですが、$\alpha$がどういう値になるときに解の個数が少なくなるでしょうか？

(1)の証明を思い出すと、$\theta=\frac{\pi}{4},\,\frac{3\pi}{4},\,\cdots$のときに正負が切り替わっていることが解の個数に重要であるので、例えば$\theta=\frac{\pi}{4}$を代入した値が$0$になったりすると解の個数が少なくなってしまうことが想像できます。

 

そこで、$\theta=\frac{\pi}{4}$を代入して、

\[1-\sin\left(\alpha+\frac{\pi}{4}\right)=0\]

となるとき、例えば$\alpha=\frac{\pi}{4}$のときに解の個数が少なくなっていると予想してそのときの方程式を解いていってあげるとよいでしょう。

$2x^2+y^2=\frac{1}{4}$かつ$\alpha=\frac{\pi}{4}$のとき、すなわち、$(x,\,y)=\left(\frac{1}{4},\,-\frac{1}{2\sqrt{2}}\right)$のときの法線は、

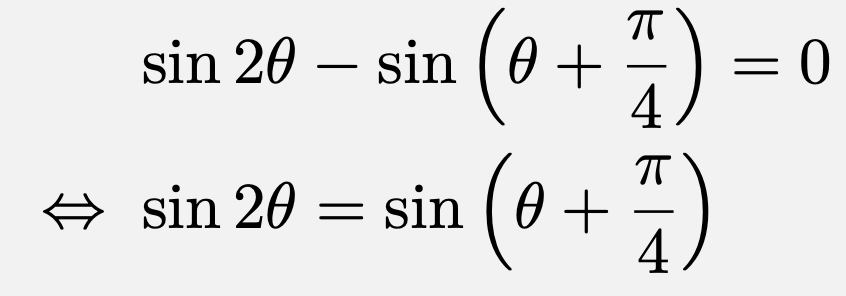
\begin{align*}&\sin2\theta-\sin\left(\theta+\frac{\pi}{4}\right)=0\\\Leftrightarrow &\sin2\theta=\sin\left(\theta+\frac{\pi}{4}\right)\end{align*}

$0\leqq \theta\leqq 2\pi$の範囲でこれを満たすのは、$\theta=\frac{\pi}{4},\,\frac{\pi}{12},\,\frac{19}{12}\pi$の3つのみなので、4個以上の解を持たない。

したがって、$2x^2+y^2=\frac{1}{4}$上に存在する点$(x,\,y)=\left(\frac{1}{4},\,-\frac{1}{2\sqrt{2}}\right)$は条件を満たさないので、領域$D$はこれを含んではいけない。つまり、$r\leqq \frac{1}{2}$が必要。

以上より、条件を満たす$r$の最大値は$\boldsymbol{\frac{1}{2}}$

まとめ

第四問や第六問が難しく、2019年度と比べると2020年度は難化していると思います。また、出題分野については、東大が好んで出す確率や複素数平面などが一切出てこなかったため、いつもと変わった出題の年だと言えるでしょう。第五問のような断面を考えて体積を求めさせる問題はよく出題されるので、出来なかった場合にはよく復習しておくべきです。

 

第一問、第二問、第五問など、易しい問題も含まれているので、これらの問題から取り組み始められたかどうかが合否を左右したと思われます。

理三志望であれば、第四問の(2)以降と第六問(2)以外を取りきって、80〜90点くらいを狙いたい内容です。理一理二志望であれば、第一問、第二問、第五問をほぼ完答して、残りで部分点を取って60〜70点を狙えるとよいでしょう。

東大数学過去問カテゴリの最新記事