「東大数学の対策をする上で、まず何からやればいいんだろう…」
と悩んでいませんか?
大学受験の対策をし始めるときには、過去問を解いたり、基礎固めをすることも重要ですが、まずは、頻出分野が何なのかを把握しておくことが最も重要です。
そこで、近年の出題傾向から、東大受験生なら絶対に重点的に学んでおいた方がいい数学の3分野を現役東大医学部生の私が教えたいと思います!
また、それぞれの頻出分野で出された東大模試の問題を1題ずつピックアップして、それぞれの問題について私が解説をしていきます!
これを読めば、東大入試の傾向を把握できるはずです!
東大受験直前期に対策すべき数学の3分野
東大受験で絶対に対策しておくべき数学の3分野は以下の3つです。
1.確率(特に確率漸化式)
2.複素数平面(理系のみ)
3.空間図形の求積問題
それぞれについて解説していきます!
【対策すべき分野1】確率
東大数学ではほぼ毎年確率の問題が出ているのは東大受験生ならよく知っているでしょう。2018年度は確率の問題が出題されないという非常に稀な年でしたが、基本的には東大は確率の問題を出すのが好きだと思っておいた方がよいでしょう。
確率の中でもよく出題されるのは、確率漸化式の分野です。確率漸化式は確率と数列を絡めた問題であり、2分野の知識をまとめて問うことができるので、過去に何度も出題されています。
理系は6問、文系は4問しか出題できない入試問題で、複数の分野の理解をまとめて問うことができるのは、東大としても数学の総合力を見るのに便利ですよね。
確率の分野を学び、さらに確率漸化式は重点的に学んでおくとよいでしょう。
2018年の東大模試では秋の東大実戦で確率漸化式の問題が出題されていました。まだ解いたことがない人は取り組んでみるとよいでしょう。
$n$は$2$以上の整数とする。サイコロを$n$回振り、出た目の数を順に$a_1,\,a_2,\,\cdots,\,a_n$とする。$1\leqq k\leqq n-1$を満たすすべての整数$k$に対して$a_ka_{k+1}$が$3$の倍数となる確率$p_n$を求めよ。
ただし、サイコロは1から6までの目が等確率で出るものとする。
簡単に解説をしていきます。
「『2連続で$3$の倍数が出ない』ことがない」確率を求めればいいわけですが、$n$個ある数字のどの2つを取っても2連続で$3$の倍数でないことがないように並べるのは難しいですよね。
「もともと条件を満たしていている数列があってそこに新たに数字を付け加えるなら簡単なのにな…」と思いたくなるところですが、そういうときは漸化式を立ててあげればいいんでしたね!
数字を付け加えるときに、末尾が$3$の倍数ならどんな数を付け加えても条件を満たしていますが、$3$の倍数でないときは$3$の倍数を付け加えないと条件を満たさなくなってしまいますよね。
そこで、「$a_n$が$3$の倍数であって、『2連続で$3$の倍数が出ない』ことがない確率」を$q_n$、「$a_n$が$3$の倍数でなくて、『2連続で$3$の倍数が出ない』ことがない確率」を$r_n$とおくことにしましょう。そうすると、推移図は以下のようになります。

よって、上図より、
\[\left\{\begin{array}{l}q_{n+1}=\frac{1}{3}q_n+\frac{1}{3}r_n\\r_{n+1}=\frac{2}{3}q_n\end{array}\right.\]
となります。連立漸化式が出てきたので、これを解くだけですね。連立漸化式の解き方を復習すると、
連立漸化式の解法
- 数列が対称になっている場合には2式を足し引きをする
- 対称でない時には、1つ目の式+2つ目の式×$\alpha$が等比数列の形になるような$\alpha$を求める
無理矢理等比数列の形に変形するのがポイントでしたね。連立漸化式の解き方を忘れてしまったという人にはこちらの記事がおすすめです。
今回の問題では、$\alpha =\frac{1}{2},\,-1$と求まるので、先程の漸化式は、
\[\left\{\begin{array}{l}q_{n+1}+\frac{1}{2}r_{n+1}=\frac{2}{3}\left(q_n+\frac{1}{2}r_n\right)\\q_{n+1}-r_{n+1}=-\frac{1}{3}\left(q_n-r_n\right)\end{array}\right.\]
と変形することができますね。$q_1=\frac{1}{3},\,r_1=\frac{2}{3}$であることから、
\[\begin{align*}&\left\{\begin{array}{l}q_n+\frac{1}{2}r_n=\left(\frac{2}{3}\right)^n\\q_n-r_n=\left(-\frac{1}{3}\right)^n\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}q_n=\left(\frac{2}{3}\right)^{n+1}-\left(-\frac{1}{3}\right)^{n+1}\\r_n=\left(\frac{2}{3}\right)^{n+1}+2\left(-\frac{1}{3}\right)^{n+1}\end{array}\right.\end{align*}\]
したがって、$p_n=q_n+r_n$であることから、
\[\boldsymbol{p_n=2\left(\frac{2}{3}\right)^{n+1}+\left(-\frac{1}{3}\right)^{n+1}}\]
となります。
【対策すべき分野2】複素数平面
これは理系だけの話になってしまいますが、複素数平面も近年頻出になっています。複素数平面が理系の出題範囲に含まれるようになったのは2015年からですが、2015年は複素数平面を学校で教えられていない浪人生を考慮して複素数平面の出題は控えられました。
その後、2016年以降、2016年第4問、2017年第3問、2018年第5問、と立て続けに出題されており、東大側が複素数平面の出題をいかに好んでいるかが分かると思います。
複素数平面では、複素数に関する知識だけではなく、軌跡・領域の問題と絡めたり、図形の相似と絡めたりと、分野横断型の出題を簡単にすることができます。
近年では、複素数の軌跡・領域の問題ばかりが出されており、2019年も同様の出題がなされるのではないかと予想されます。
2018年に4回行われた東大模試でも、複素数平面の出題は毎回されています。秋の東大実戦に出された複素数平面の問題は、複素数平面で考えることを明示しておらず、自分で複素数平面を設定しなければならないやや難しい問題でした。
$\mathrm{OA}=\mathrm{OB}$である二等辺三角形$\mathrm{OAB}$と$\mathrm{OC}=\mathrm{OD}$である二等辺三角形$\mathrm{OCD}$は相似であり、合同ではないとする。ただし、3点$\mathrm{O},\,\mathrm{A},\,\mathrm{B}$はこの順に反時計回りにあり、3点$\mathrm{O},\,\mathrm{C},\,\mathrm{D}$もこの順に反時計回りにある。
点$\mathrm{E}$を三角形$\mathrm{BCE}$が$\mathrm{EB}=\mathrm{EC}$の直角二等辺三角形であり、3点$\mathrm{B},\,\mathrm{C},\,\mathrm{E}$がこの順に反時計回りにあるようにとる。また、点$\mathrm{M}$を線分$\mathrm{AD}$の中点とする。
3点$\mathrm{O},\,\mathrm{E},\,\mathrm{M}$が同一直線上にあるとき、$\angle{\mathrm{AOB}}$の大きさを求めよ。
このように自分で複素数平面を設定しなければならないタイプの問題がそろそろ出題されてもよいのではないかと考えています。
この問題について簡単に解説をしていきます。
まずは、二等辺三角形をなす、直角二等辺三角形をなすなどの条件が複素数の回転を用いれば簡単に表せることに注目して点$\mathrm{O}$を原点とする複素数平面上で考えることにします。
さらに、原点を中心として適切に回転、拡大縮小すれば、点$\mathrm{A}$に対応する複素数を$1$に持ってくることができます。(このとき回転と拡大縮小をしても求める角度は変わりません)
ここまで来れば、問題を解く準備はバッチリです。点$\mathrm{B}$、$\mathrm{C}$に対応する複素数をそれぞれ$b,\,c(bは実軸の上側になるようにする)$とすれば、$b$をかけることは点$\mathrm{A}$を原点を中心に$\angle\mathrm{A}\mathrm{O}\mathrm{B}$だけ回転する操作に対応するので、題意より、点$\mathrm{D}$に対応する複素数は$bc$となることがわかります。
よって、点$\mathrm{M}$に対応する複素数は$\frac{1+bc}{2}$だと分かりますね。
また、点$\mathrm{E}$についての条件から、点$\mathrm{E}$に対応する複素数を$e$とすれば、
\[\frac{c-e}{b-e}=i\]
が成り立ちます。
最後に、3点$\mathrm{O},\,\mathrm{M},\,\mathrm{E}$が一直線上になるための条件を考えれば、問題文にある条件をすべて表せたことになります。この条件は、
\[e=k\frac{1+bc}{2}\]
を満たすような実数$k$が存在する。という条件になりますが、このままでは扱いづらいです。
そこで、複素数について、実数や純虚数を数式で表す方法を復習しましょう。
ある複素数$\beta$について、
\[\beta が純虚数\Leftrightarrow \beta+\overline{\beta}=0\]
\[\beta が実数\Leftrightarrow \beta-\overline{\beta}=0\]
この知識を使えば、$|b|=1,\,|c|\ne1$であることから$bc\ne -1$である点にも注意して、
\[e=k\frac{1+bc}{2}\Leftrightarrow \frac{k}{2}=\frac{e}{1+bc}\]
と変形できるので、先ほどの条件は、
\[\frac{e}{1+bc}-\overline{\left(\frac{e}{1+bc}\right)}=0\]
とできます。文字3つあるのに、条件式はこれと$\frac{c-e}{b-e}=i$の2つしかない点が非常に気になりますが、とりあえず問題文に与えられた条件はすべて数式化することに成功しているので、このまま進めていきましょう。
文字の対称性を考えると$e$を消去するのが良さそうなので、$e$を消去してみます。
\[\frac{c-e}{b-e}=i\Leftrightarrow c-e=(b-e)i\Leftrightarrow e=\frac{c-bi}{1-i}\]
となるので、これをもう一つの式に代入して、$|b|=1$であることに注意して変形していくと、
ここで、$|c|\ne 1$であることから、
\[\begin{align*}&(b-\bar{b}i)=0\\\Leftrightarrow &b^2-|b|^2i=0\\\Leftrightarrow &b^2=i\\\Leftrightarrow &b=\pm\frac{1+i}{\sqrt{2}}\end{align*}\]
$b$は実軸の上側の点であることから$b=\frac{1+i}{\sqrt{2}}$と分かるので、求める角度は、
\[\boldsymbol{\angle{\mathrm{AOB}}=45^{\circ}}\]
とわかります。
【対策すべき分野3】空間図形の求積問題
東大では空間図形の求積問題も頻出です。近年では、2016年第6問、2017年第6問、2018年第6問、と毎年出題されています。(空間図形の問題は図を描かなければいけないことが多いので、解答用紙の大きさが他の2倍ある第6問に出題されていることが多いです。)
空間図形の問題は、求積問題にすることで文字固定の考え方をしっかりと運用できるかどうかについても問うことができます。体積を求めるときには例えば$x=k$などの適切な断面を取ってから、その図形を図示するなりして面積を求め、それを積分によって求めることがほとんどですよね。
文字固定は多変数関数の最大最小問題や、軌跡・領域の順像法の考え方にも出てくる数学の中でも非常に大切な手法であることから求積問題の出題頻度は高くなっているのだと思われます。
さて、2018年の東大模試ではやはり空間図形の問題は出されており、夏に1題、秋に1題出題されています。秋の東大実戦の問題は空間図形を切断して最後に体積を求めさせるという実に東大っぽい問題になっていました。
$\mathrm{O}$を原点とする$xyz$空間において、
を頂点とする立方体の内部および表面を$C$とし、表面を$D$とする。また、$\mathrm{O}$を頂点とし、正方形$\mathrm{A_1A_2A_3A_4}$を底面とする正四角錐の内部および表面を$E$とする。
$xyz$空間の2点$\mathrm{P},\,\mathrm{Q}$に対して、$\mathrm{P}$と$\mathrm{Q}$を$x$軸または$y$軸または$z$軸に平行な線分からなる折れ線で結ぶときの経路の長さの最小値を$d(\mathrm{P},\,\mathrm{Q})$で表す。
$C$に含まれる点$\mathrm{P}$に対して、$\mathrm{Q}$を$D$上で動かしたときの$d(\mathrm{P},\,\mathrm{Q})$の最小値を$m(\mathrm{P})$で表す。このとき、$m(\mathrm{P})\geqq d(\mathrm{O},\,\mathrm{P})$を満たす点$\mathrm{P}$全体の作る立体を$F$とする。
(1)$E$に含まれる点$\mathrm{P}(x,\,y,\,z)$に対して、$m(\mathrm{P})$を$\mathrm{P}$の座標を用いて表わせ。
(2)$0\leqq t\leqq 1$を満たす実数$t$に対して、平面$z=t$による$E$と$F$の共通部分の切り口の面積を$S(t)$とおく。ただし、切り口が空集合のときは、$S(t)=0$と定める。$S(t)$を求めよ。
(3)$F$の体積を求めよ。
この問題について簡単に解説をしていきます。
まず、(1)について。
座標空間にある立方体についての問題なので、空間の図を描きたくなるところですが、立体の図を描いても大した情報が得られず余計ややこしくなってしまうことが多いので、あくまで断面で考えたり、代数的に考えることにつとめましょう。
まずは、問題文の中に出てくる$d(\mathrm{P},\,\mathrm{Q})$というものの定義についてですが、結局これは、2点を対角線とする直方体の3辺の長さの和ということですよね。ややこしく書いているのは、$x,\,y,\,z$成分のどれかが一致してしまったときに直方体にはならないことなどが理由でしょう。以下のように数式で書けばわかりやすいと思います。
$xyz$空間の2点$\mathrm{P}(x_1,\,y_1,\,z_1),\,\mathrm{Q}(x_2,\,y_2,\,z_2)$に対して、$\mathrm{P}$と$\mathrm{Q}$を$x$軸または$y$軸または$z$軸に平行な線分からなる折れ線で結ぶときの経路の長さの最小値を$d(\mathrm{P},\,\mathrm{Q})$とすると、
\[d(\mathrm{P},\,\mathrm{Q})=|x_1-x_2|+|y_1-y_2|+|z_1-z_2|\]
さて、$d(\mathrm{P},\,\mathrm{Q})$の定義が数式でしっかりと解釈できればあとは簡単です。ある$C$に含まれる点$\mathrm{P}(x,\,y,\,z)$が与えられたときに、点$\mathrm{Q}$は立方体の面上を動くことから、どれか1つの座標が$\pm 1$になっており、それ以外の座標は$-1$から$1$までを自由に動くことができます。
よって、たとえば$x$座標を$1$と固定したときは、$y,\,z$座標は点$\mathrm{P}$と同じときに最小値を取るので、$|1-x|$が最小値だとわかりますね。これを他の場合でも同様に議論していけば、最小値の候補は、
\[|1-x|,\,|1+x|,\,|1-y|,\,|1+y|,\,|1-z|,\,|1+z|\]
の6つだとわかります。さらに、$x,\,y,\,z$の正負で場合分けして考えてみると、
\[1-|x|,\,1-|y,|\,1-|z|\]
が最小値の候補だとわかります。このうち最も小さいものの1つが最小値になるので、
\[m(\mathrm{P})=\mathrm{min}\{1-|x|,\,1-|y,|\,1-|z|\}\]
と非常にシンプルに表すことができました!
さて、今回の問題では、点$\mathrm{P}$は$E$に含まれる点という条件になっているので、
\[z\geqq |x|,\,z\geqq |y|\]
という条件が付いていますね。よって、
\[\boldsymbol{m(\mathrm{P})=1-z}\]
となります。
次に(2)について。
$E$と$F$の共通部分の断面を考えるのはそれぞれの方程式に$z=t$を代入するだけでOKですね。何度も言っていますが、こういうときに立体ではなく断面や代数で考えることがポイントになります。
実際に$z=t$を代入してみると、
\[\begin{align*}&1-t\geqq |x|+|y|+t ,\, t\geqq |x|,\,t\geqq |y|\\\Leftrightarrow &|x|+|y|\leqq 1-2t,\,|x|\leqq t,\,|y|\leqq t\end{align*}\]
というのが条件になります。平面上に図示してみると、正方形とひし形の共通部分になっていることがわかりますね。さらに、$t$が増加するとひし形は小さくなっていき、正方形は大きくなっていくので、場合分けが生じることはすぐにわかります。動画で見てみると以下のようになります。
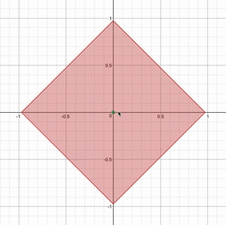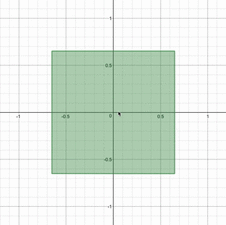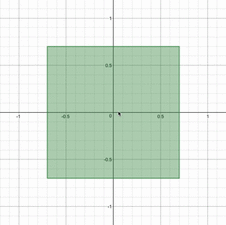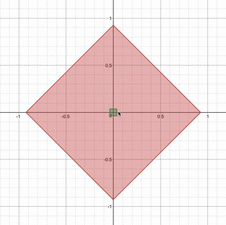
さて、実際に場合分けをして議論していきましょう。(i)正方形がひし形の中に含まれるとき(ii)共有点をもつ時、(iii)ひし形が正方形の中に含まれる時、の3つで場合分けをすれば良さそうです。答案例を示すと以下のようになります。
(i)$\frac{1-2t}{2}\geqq t$すなわち$0\leqq t\leqq\frac{1}{4}$のとき、断面は以下の斜線部のようになる。
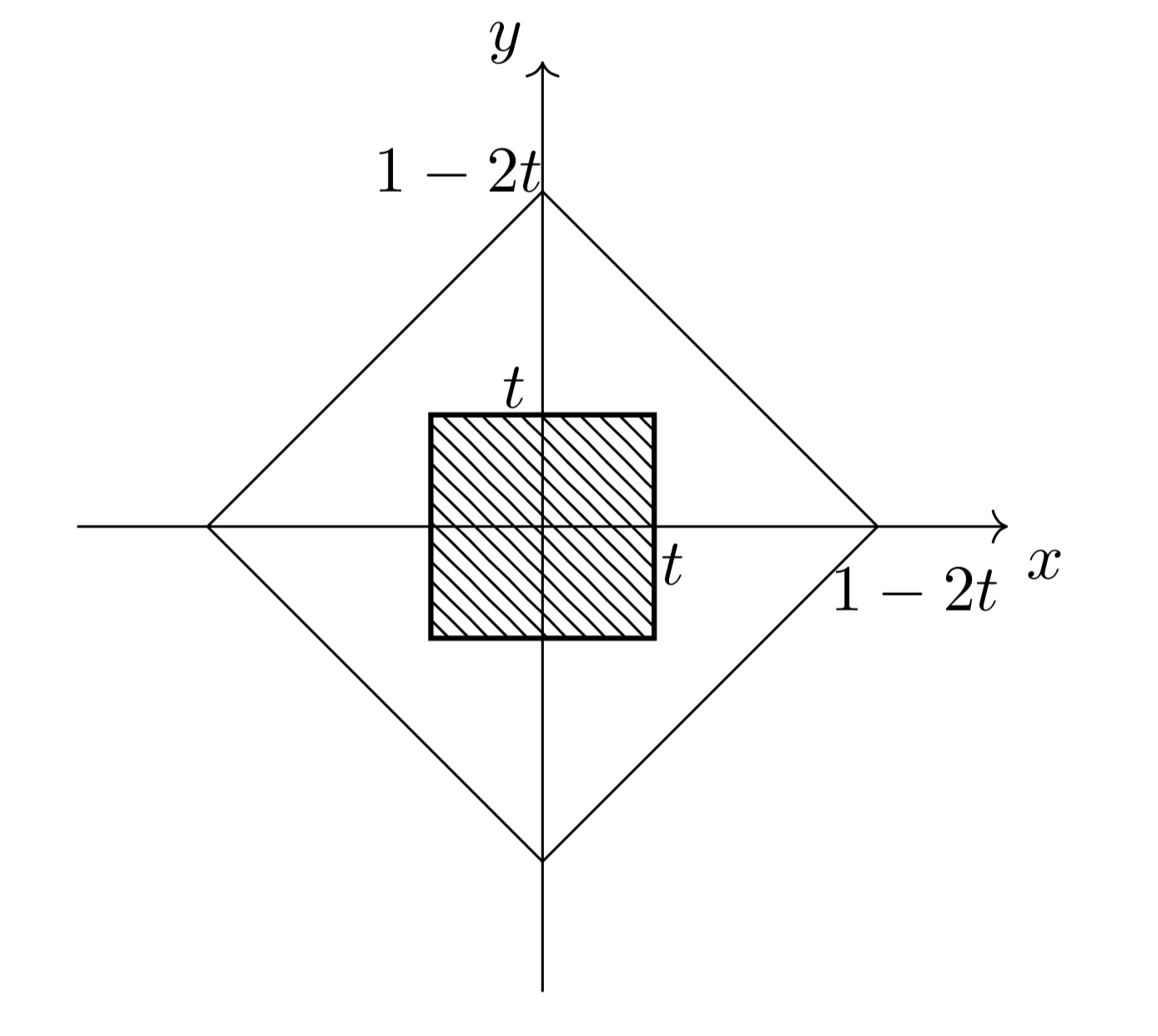
このとき、$S(t)=4t^2$である。
(ii)$\frac{1-2t}{2}\leqq t\leqq 1-2t$すなわち$\frac{1}{4}\leqq t\leqq\frac{1}{3}$のとき、断面は以下の斜線部のようになる。
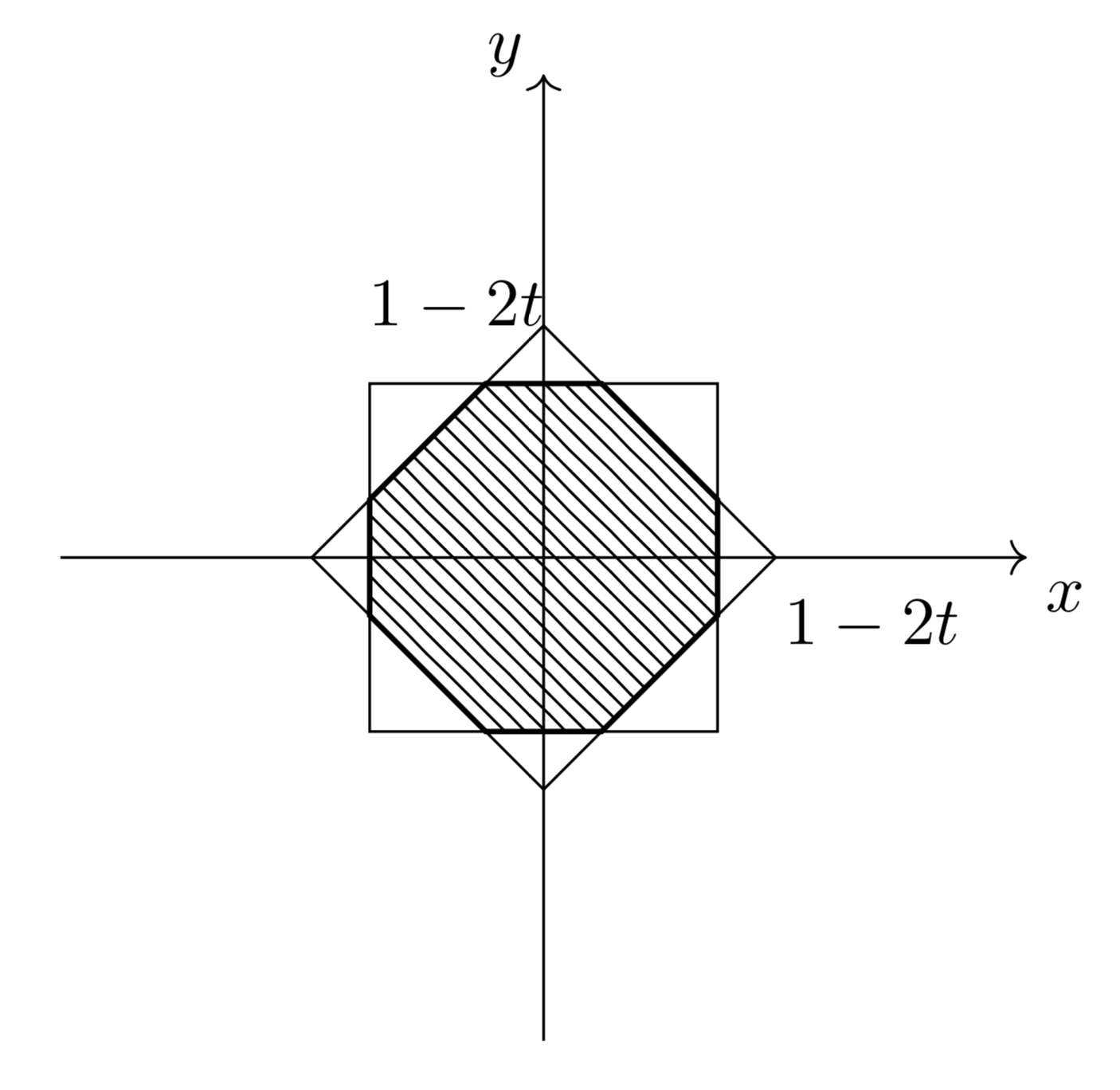
このとき、
\[S(t)=4t^2-2(4t-1)^2=-28t^2+16t-2\]
である。
(iii)$0\leqq 1-2t\leqq t$すなわち$\frac{1}{3}\leqq t\leqq\frac{1}{2}$のとき、断面は以下の斜線部のようになる。
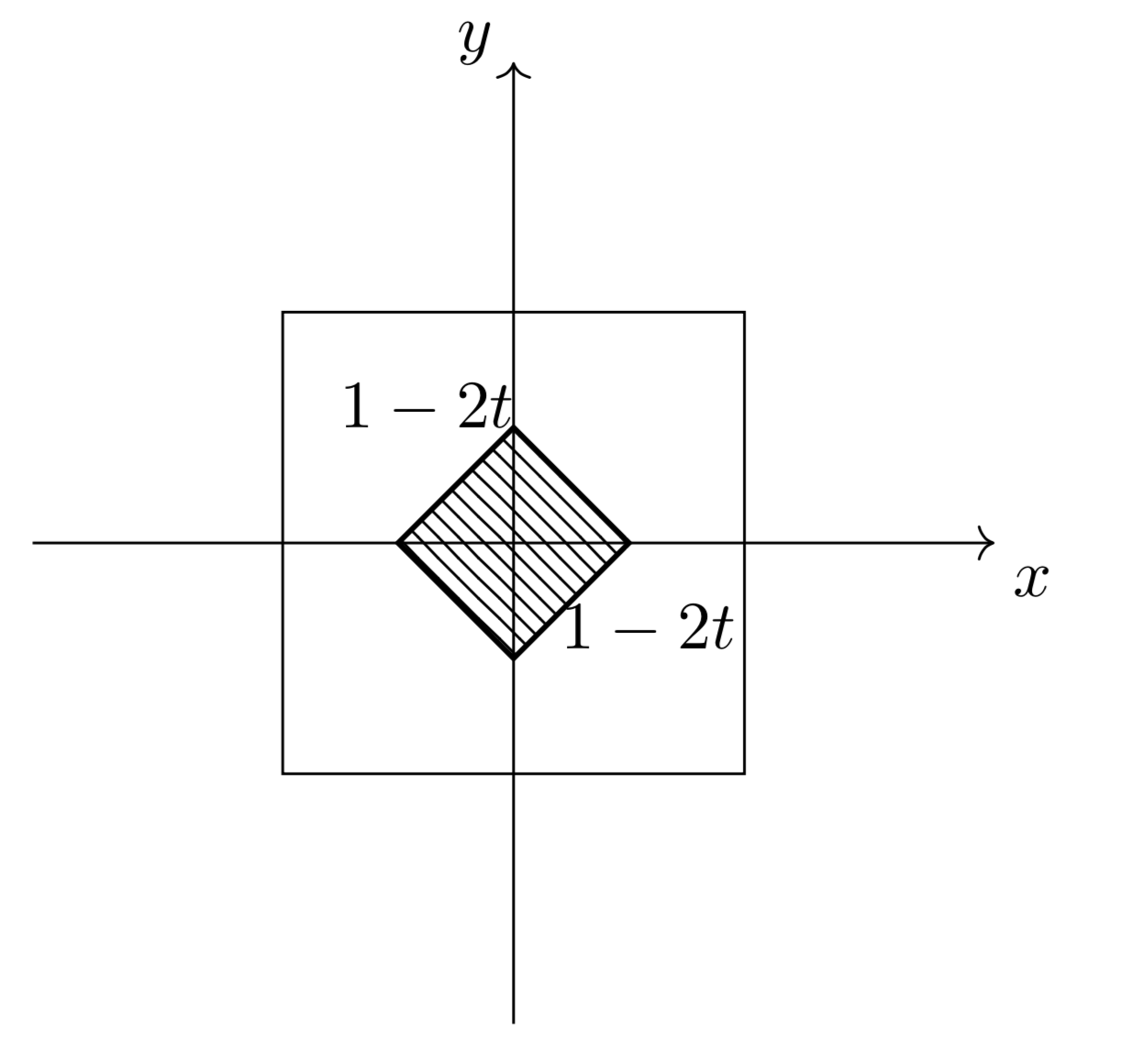
このとき、$S(t)=2(1-2t)^2$である。
(iv)$\frac{1}{2}\leqq t\leqq 1$のとき、$S(t)=0$である。
以上より、
\[\left\{\begin{array}{l}\boldsymbol{S(t)=4t^2\left(0\leqq t\leqq\frac{1}{4}のとき\right)}\\\boldsymbol{S(t)=-28t^2+16t-2\left(\frac{1}{4}\leqq t\leqq\frac{1}{3}のとき\right)}\\\boldsymbol{S(t)=2(2t-1)^2\left(\frac{1}{3}\leqq t\leqq\frac{1}{2}のとき\right)}\\\boldsymbol{S(t)=0\left(\frac{1}{2}\leqq t\leqq 1のとき\right)}\end{array}\right.\]
場合分けがしっかりできれば難しくない問題ですが、図を3つも描かなければならないので記述が少々面倒でしたね。
最後に(3)について。
あとは(2)で求めた$S(t)$を$t$で積分するだけです!ただし注意したいのが、積分して求まる体積は求めたい体積の$\frac{1}{6}$倍であるということです。体積を求めたい図形の対称性からその$\frac{1}{6}$倍の図形を求めさせる誘導になっているので、最後に$6$倍し忘れないように気をつけましょう。
(2)の結果より、$E$と$F$の共通部分の体積は、
まとめ
・直前期に東大数学で対策すべきは確率、複素数平面、空間図形の3分野
・確率は特に確率漸化式を対策すべき
・複素数平面は軌跡・領域や図形の相似と絡めた出題に注意
・空間図形は求積問題が頻出





