※以下の解答・解説は当ブログのオリジナルのものであり東京大学が公表しているものではありません。
私がおすすめする過去問題集について説明した記事はこちら↓
第一問
第一問は以下のような出題でした。

第一問の難易度分析
三角関数と微分に関する非常に易しい問題です。
(1)は三角関数についての基本的な定理を覚えていれば一瞬で解ける問題であり、確実に得点したいところです。
(2)も微分ができれば何も難しいところはありません。
短い時間で完答したい問題でしょう。
第一問(1)を解く上での考え方・ポイント
$x=\cos\theta$の整式で表わすためには、三角関数に関する基本的な公式を知っている必要がありますが、受験生が忘れている可能性が高いのは3倍角の公式だけでしょう。
3倍角の公式
\[\left\{\begin{array}{l}\cos3\theta=4\cos^3\theta-3\cos\theta\\\sin3\theta=-4\sin^3\theta+3\sin\theta\end{array}\right.\]
これは覚えずに毎回導出している受験生の方が多いかと思いますが、私としては覚えておいた方がよいと思っています。
語呂合わせでコサインの3倍角の公式を覚えておいて、「コサインとサインを入れ替えて符号を逆にするとサインの3倍角の公式になる」という風に2つの公式を暗記しています。
以下、解答例を示しておきます。
\[\begin{align*}&\cos 3\theta+a\cos 2\theta+b\cos \theta\\=&4\cos^3\theta-3\cos\theta+a(2\cos^2\theta -1)+b\cos\theta\\=&4\cos^3\theta+2a\cos^2\theta+(b-3)\cos\theta-a\end{align*}\]
であるから、
\[\boldsymbol{f(\theta)=4x^3+2ax^2+(b-3)x-a}\]
また、
\[\begin{align*}&\frac{f(\theta)-f(0)}{\cos\theta-1}\\=&\frac{4(x^3-1)+2a(x^2-1)+(b-3)(x-1)}{x-1}\\=&4(x^2+x+1)+2a(x+1)+b-3\\=&4x^2+2(a+2)x+2a+b+1\end{align*}\]
であるから、
\[\boldsymbol{g(\theta)=4x^2+2(a+2)x+2a+b+1}\]
第一問(2)を解く上での考え方・ポイント
最小値についての考察なので反射的に微分をしてしまいそうになりますが、$g(\theta)$は2次関数なので平方完成をしてあげればOKです。軸の位置と頂点の$y$座標の値が$0$になるという2つの条件を考えることになります。
\[\begin{align*}&4x^2+2(a+2)x+b+1\\=&4\left(x+\frac{a+2}{4}\right)^2-\frac{(a+2)^2}{4}+2a+b+1\\=&4\left(x+\frac{a+2}{4}\right)^2-\frac{(a-2)^2}{4}+b+1\end{align*}\]
であるから、$0<\theta<\pi$のとき、$-1<x<1$であることも考えると、求める条件は、
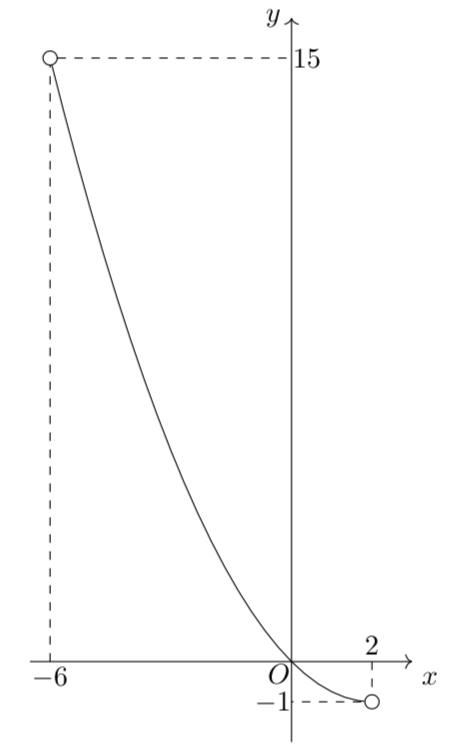
\[\begin{align*}&-1<-\frac{a+2}{4}<1,\,-\frac{(a-2)^2}{4}+b+1=0\\\Leftrightarrow &\boldsymbol{-6<a<2,\,b=\frac{(a-2)^2}{4}-1}\end{align*}\]
これを図示すると、以下の実線部。(ただし、白丸は含まない)
第二問
第二問は以下のような出題でした。

第二問の難易度分析
確率に関する非常に易しい問題です。
東大の出題意図を汲み取りながら解くとなると、少し発想力が必要となりますが、ただただシンプルに計算をしていくだけで答えが求まる問題なので、多くの人が完答したものと思われます。
第二問(1)を解く上での考え方・ポイント
「6秒後に直線$y=x$上にある」という状態の中で場合分けを行ってあげて、それぞれの確率を求めてから足してあげれば良さそうです。
6秒後に点$\mathrm{P}$が存在しうる$y=x$上の点は、$(0,\,0),\,(\pm1,\,\pm1),\,(\pm2,\,\pm2),\,(\pm3,\,\pm3)$(複号同順)の7つの点だけで、また、対称性から、$(1,\,1)$にいる確率と$(-1,\,-1)$にいる確率、$(2,\,2)$にいる確率と$(-2,\,-2)$にいる確率、$(3,\,3)$にいる確率と$(-3,\,-3)$にいる確率はそれぞれ等しいので、4パターンの確率を計算してあげれば十分だとわかります。
以下、解答例を示しておきます。
6秒後に点$\mathrm{P}$が存在しうる$y=x$上の点は、$(0,\,0),\,(\pm1,\,\pm1),\,(\pm2,\,\pm2),\,(\pm3,\,\pm3)$(複号同順)の7つの点だけある。
(i)$(0,\,0)$にある場合
右に移動する回数と左に移動する回数が等しく、上に移動する回数と下に移動する回数が等しければいいので、確率は、
\[\begin{align*}&2\cdot_6\mathrm{C}_3\left(\frac{1}{4}\right)^6+2\cdot_6\mathrm{C}_2\cdot_4\mathrm{C}_2\cdot_2\mathrm{C}_1\left(\frac{1}{6}\right)^6\\=&\frac{25}{256}\end{align*}\]
(ii)$(1,\,1)$にある場合
左に移動する回数よりも右に移動する回数が1回多く、下に移動する回数よりも上に移動する回数が1回多ければよいので、確率は、
\[\begin{align*}&2\cdot_6\mathrm{C}_3\cdot_3\mathrm{C}_2\left(\frac{1}{4}\right)^6+_6\mathrm{C}_2\cdot_4\mathrm{C}_2\cdot_2\mathrm{C}_1\left(\frac{1}{4}\right)^6\\=&\frac{75}{1024}\end{align*}\]
対称性より、$(-1,\,-1)$にある場合もこの確率に等しい。
(iii)$(2,\,2)$にある場合
左に移動する回数よりも右に移動する回数が2回多く、下に移動する回数よりも上に移動する回数が2回多ければよいので、確率は、
\[\begin{align*}&2\cdot_6\mathrm{C}_3\cdot_3\mathrm{C}_2\left(\frac{1}{4}\right)^6\\=&\frac{15}{512}\end{align*}\]
対称性より、$(-2,\,-2)$にある場合もこの確率に等しい。
(iv)$(3,\,3)$にある場合
右に3回移動し、上3回移動すればよいので、確率は、
\[\begin{align*}&_6\mathrm{C}_3\left(\frac{1}{4}\right)^6\\=&\frac{5}{1024}\end{align*}\]
対称性より、$(-3,\,-3)$にある場合もこの確率に等しい。
以上より、求める確率は、
\[\frac{25}{256}+2\cdot\frac{75}{1024}+2\cdot\frac{15}{512}+2\cdot\frac{5}{1024}=\boldsymbol{\frac{5}{16}}\]
このように、対称性を意識して計算量を減らしつつ、場合分けをしていってしまうという解法でも悪くないでしょう。この解法の場合は、(2)の答えが計算過程で求まっているので、一瞬で(2)が終わるのが良い点です。
しかしながら、東大が求めている解法は上の解法ではないと思われます。$y=x$という直線に意識を向けさせていることから、点$\mathrm{P}$がどの直線上に乗っているのかというのを意識すると以下のような解法が思いつくはずです。
別解
点$\mathrm{P}$は、直線$y=x+k(kは整数)$上に存在し、右もしくは下に移動すると$k$の値は1だけ小さくなり、上もしくは左に移動すると$k$の値は1だけ大きくなる。
よって、6秒後に点$\mathrm{P}$が直線$y=x$上に存在することは、「右または下に移動した回数」と「上または左に移動に移動した回数」が等しいことと同値である。
したがって、求める確率は、
\[_6\mathrm{C}_3\left(\frac{1}{2}\right)^6=\boldsymbol{\frac{5}{16}}\]
この別解で解くと、非常に短い時間で(1)の答えを得ることができますね!
第二問(2)を解く上での考え方・ポイント
本解で解いた場合にはすでに答えが求まっているので、それを書くだけで終わりですね。
(1)の過程より、$\boldsymbol{\frac{25}{256}}$
別解で解いた場合にはどうすればよいでしょうか?
別解では「どの直線上にあるか」ということを意識していたので、原点$O$にあるというのは、「$y=x$上にあり、かつ、$y=-x$上にある」と言い換えることができますね。
対称性を考えれば、6秒後に$y=-x$にある確率は(1)で求めた確率に等しいです。よって、2つの事象が独立であることを考えれば、以下のような解答が作れます。
別解
6秒後に$y=-x$にある確率は対称性より(1)で求めた確率に等しく、$\frac{5}{16}$。原点$O$にあるとき「$y=x$上にあり、かつ、$y=-x$上にある」から、求める確率は、
\[\left(\frac{5}{16}\right)^2=\boldsymbol{\frac{25}{256}}\]
あまり深く考えずに解いても本解のようにして解けるので、この設問での点数差はつきにくいものの、全体での時間的な余裕が変わる点では重要な問題だったと言えるでしょう。
第三問
第三問は以下のような出題でした。

第三問の難易度分析
標準的な難易度の複素数平面の問題です。複素数平面の軌跡に関する問題は東大では頻出であり、このレベルの問題は解けないとまずいでしょう。
特に、今回の問題は$w=\frac{1}{z}$という変換を行っており、これは「反転」という有名な変換に非常に似た変換です。反転についての知識があると結果が少し見えていてミスが減ることになったでしょう。
反転について説明した記事はこちら↓
第三問(1)を解く上での考え方・ポイント
反転の性質として、「直線を反転させると円になる」という関係が知られています。今回の問題では円になることが問題文ですでに述べられていますね。
円の方程式になるように平方完成することが最終的な目標だということを考えておくと、垂直二等分線の式を立ててから両辺に$\left|\frac{w}{\alpha}\right|$をかけるだけで円の方程式になることに気づきます。
以下に解答例を示しておきます。
点$z$が直線$L$上を動くとき、
\[|z|=|z-\alpha|\]
をみたす。このとき、$w\ne 0$のもとで、$z=\frac{1}{w}$であるから、これを上の式に代入して、
\[\begin{align*}&\left|\frac{1}{w}\right|=\left|\frac{1}{w}-\alpha\right|\\\Leftrightarrow &\left|\frac{1}{\alpha}\right|=|w-\frac{1}{\alpha}|\end{align*}\]
よって、
\[\boldsymbol{円の中心は\frac{1}{\alpha},\,半径は\left|\frac{1}{\alpha}\right|}\]
1点を除いたものになると問題文に書かれていますが、除く点は$0$であることがわかりますね。
第三問(2)を解く上での考え方・ポイント
反転の基礎知識を持っていると、原点を通らない直線に対して$w=\frac{1}{z}$の変換を施したものは原点を通る円になることがわかるので、線分を動く場合は軌跡が原点を通る円の一部になることがわかります。
さて、代数的にこれを処理していきましょう。複数平面上において直線を扱うときには垂直二等分線の形で扱うのが最も扱いやすいので、「点$\beta$と点$\beta^2$を結ぶ線分」も何かの線分の垂直二等分線として扱えないか考えてみます。すると、実部がどちらも$-\frac{1}{2}$であることから、$0$と$-1$を結ぶ線分の垂直二等分線だということがわかりますね!
あとは、「線分である」という条件を考えなければなりません。線分という条件は考えにくいので、$z$と$0$の距離が$1$以下であるという条件に言い換えてあげます。そうすると、$|w|\geqq 1$という条件に言い換えることができて、軌跡の範囲を限定できそうです。
\[\beta=\frac{-1+\sqrt{3}i}{2},\,\beta^2=\frac{-1-\sqrt{3}i}{2}\]
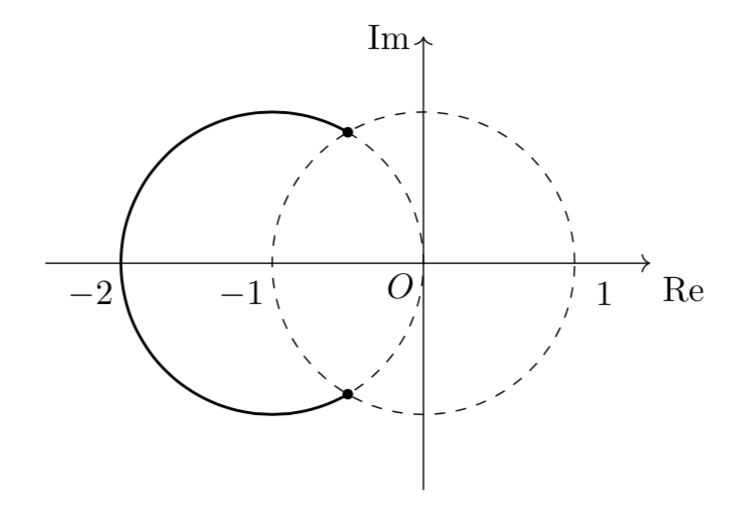
より、点$\beta$と点$\beta^2$を結ぶ線分は、「点$-1$と点$0$を結ぶ線分の垂直二等分線のうち、原点からの距離が1以下の部分」と言い換えることができる。
(1)の結果より、求める軌跡は$-1$を中心とする半径$1$の円上にあり、また、
\[|w|=\frac{1}{|z|}\]
であるから、
\[0<|z|\leqq 1\Leftrightarrow |w|\geqq 1\]
したがって、求める軌跡は以下の図の太線部。(ただし、黒丸は含む)
第四問
第四問は以下のような出題でした。

第四問の難易度分析
易しい整数問題です。$(a+\sqrt{b})^n$の形が出てくる問題を解いたことがあれば、序盤の問題は難なく解けるでしょう。この式の形は以下の性質を持つことで有名であり、入試問題でも頻出なので、押さえておくとよいでしょう。
$a,\,b$を整数、$n$を自然数としたとき、
\[(a+\sqrt{b})^n+(a-\sqrt{b})^n\]
は$n$の値によらず常に偶数となる。
$(a+\sqrt{b})^n+(a-\sqrt{b})^n$の重要な性質やそれに関する入試問題をまとめた記事はこちら↓
後半になるにつれて普通の整数問題になっていきます。やや難しい(4)のために丁寧な誘導がついているので、そこにしっかりと乗れたかどうかが完答できるかどうかの分かれ目となったでしょう。
第四問(1)を解く上での考え方・ポイント
$p=2+\sqrt{5}$、$-\frac{1}{p}=2-\sqrt{5}$であることから、上で述べた性質が使えますね!
ただただ計算していくだけの問題ですが、計算の結果がちゃんと偶数になってるかどうか確かめましょう。さらに、答えだけでよい問題なので、答えを書いておきます。
\[\boldsymbol{a_1=4},\,\boldsymbol{a_2=18}\]
第四問(2)を解く上での考え方・ポイント
$a_1=4$のような具体値を用いずに、$a_1=p-\frac{1}{p}$として処理すれば良いことに気づけばすぐに終わる問題です。
\[\begin{align*}a_1a_n=&\left(p-\frac{1}{p}\right)\left\{p^n-\left(\frac{1}{p}\right)^n\right\}\\=&p^{n+1}+\left(\frac{1}{p}\right)^{n+1}-p^{n-1}-\left(\frac{1}{p}\right)^{n-1}\\=&\boldsymbol{a_{n+1}-a_{n-1}}\end{align*}\]
第四問(3)を解く上での考え方・ポイント
$a_n$が常に自然数になるという性質の示し方は、数学的帰納法によるものと、二項定理によるものの2通りがあります。今回は(2)の結論の式を数学的帰納法に乗せてあげれば上手く示せそうですね。
$a_n$が自然数であることを数学的帰納法によって示す。
(i)$n=1,\,2$のとき、
(1)より、たしかに自然数となる。
(ii)$n=k,\,k+1(kは自然数)$のときに成立すると仮定する、すなわち、$a_k,\,a_{k+1}$が自然数であると仮定すると、(2)の式より、
\[a_{k+2}=4a_k+a_{k+1}\]
が成り立つので、$a_{k+2}$も自然数となる。
以上より、題意は示された。
別解
誘導にうまく乗れなくても、二項定理を用いれば証明可能です。
二項定理より、
\[\begin{align*}p^n=&(2^n+_nC_22^{n-2}\cdot5+\cdots)\\&+(_nC_12^{n-1}+_nC_32^{n-3}+\cdots)\sqrt{5}\end{align*}\]
であるので、自然数$b_n,\,c_n$を用いて、$p_n=b_n+c_n\sqrt{5}$と表せる。
同様にして、
\[\begin{align*}\left(-\frac{1}{p}\right)^n=&(2^n+_nC_22^{n-2}\cdot5+\cdots)\\&+(_nC_12^{n-1}+_nC_32^{n-3}+\cdots)\sqrt{5}\end{align*}\]
より、$\left(-\frac{1}{p}\right)^n=b_n+c_n\sqrt{5}$となる。
したがって、$a_n=2b_n$が分かるので、$a_n$は自然数であることが示された。
第四問(4)を解く上での考え方・ポイント
(2)の誘導が使えそうです。
\[a_{n+1}=4a_n+a_{n-1}\]
より、$a_{n+1}$と$a_n$の最大公約数は$a_n$と$a_{n-1}$の最大公約数でもあることが言えますね!(ユークリッドの互除法とかと同じです。)
この議論を繰り返していけば、$a_{n+1}$と$a_n$の最大公約数は$a_2$と$a_1$の公約数であることも言えます。あとは簡単でしょう。
以下に解答例を示しておきます。
(1)(2)より、
\[a_{n+1}=4a_n+a_{n-1}\]
であるので、$a_{n+1}$と$a_n$の最大公約数は$a_n$と$a_{n-1}$の最大公約数に等しいと言えるので、これを繰り返し用いれば、$a_{n+1}$と$a_n$の最大公約数は$a_2$と$a_1$の公約数でもあることが分かる。
(1)より、$a_1$と$a_2$の公約数は$2$であるから、求める最大公約数は$\boldsymbol{2}$
第五問
第五問は以下のような出題でした。

第五問の難易度分析
共通接線が関わる非常に易しい問題です。
まず、共通接線の求め方は、以下のように覚えておきましょう。
共通接線の求め方!
一方が2次関数のとき→微分によってもう一方における接線の式を立ててそれが接することを重解条件によって考える
両方が3次以上の関数のとき→微分によって両方において接線の式を立てて2式が一致する条件を考える
そして、(2)については解として出てこない接線が何なのか考えることができれば容易に解ける問題となっており、大問全体として簡単だったでしょう。
共通接線についてまとめられた記事はこちら。
第五問(1)を解く上での考え方・ポイント
今回の問題では、両方とも2次関数であることから、片方から微分によって接線の式を立てて、もう一方に接するための条件を考えるのがオーソドックスですが、問題文中に接線の式を$y=ax+b$とおくように指示されているので、重解条件を2度考えるのがよいでしょう。
以下、解答例を示しておきます。
直線$y=ax+b$が共通接線であるとき、$x=y^2+k$から$y$を消去した方程式
\[\begin{align*}&x=(ax+b)^2+k\\\Leftrightarrow &a^2x^2+(2ab-1)x+b^2+k=0\end{align*}\]
が重解を持つので、
\[a\ne0かつ(2ab-1)^2-4a^2(b^2+k)=0\]
また、$y=ax+b$と$y=x^2+k$から$y$を消去した方程式
\[x^2-ax+k-b=0\]
も重解を持つので、
\[a^2-4(k-b)=0\]
2式より、$a\ne0,\,-1$のもとで、
\[\begin{align*}&\left\{\begin{array}{l}-4ab+1-4a^2k=0\\a^2-4(k-b)=0\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}\boldsymbol{b=\frac{-a^3+a^2-a+1}{4a}}\\\boldsymbol{k=\frac{a^2-a+1}{4a}}\end{array}\right.\end{align*}\]
第五問(2)を解く上での考え方・ポイント
傾きが$2$の共通接線が存在するような$k$の値は、(1)で求めた式に$a=2$を代入すれば求まりますね。そのような$k$の値を元に、$a,\,b$の組を求めると、2組しかありません。
共通接線の3本目はどこに存在するのでしょうか?
(1)では$a\ne1$という条件がついていたことを思い出しましょう。$x,\,y$の対称性を考えると、常に下図のような傾き$-1$の共通接線が存在することがわかります。
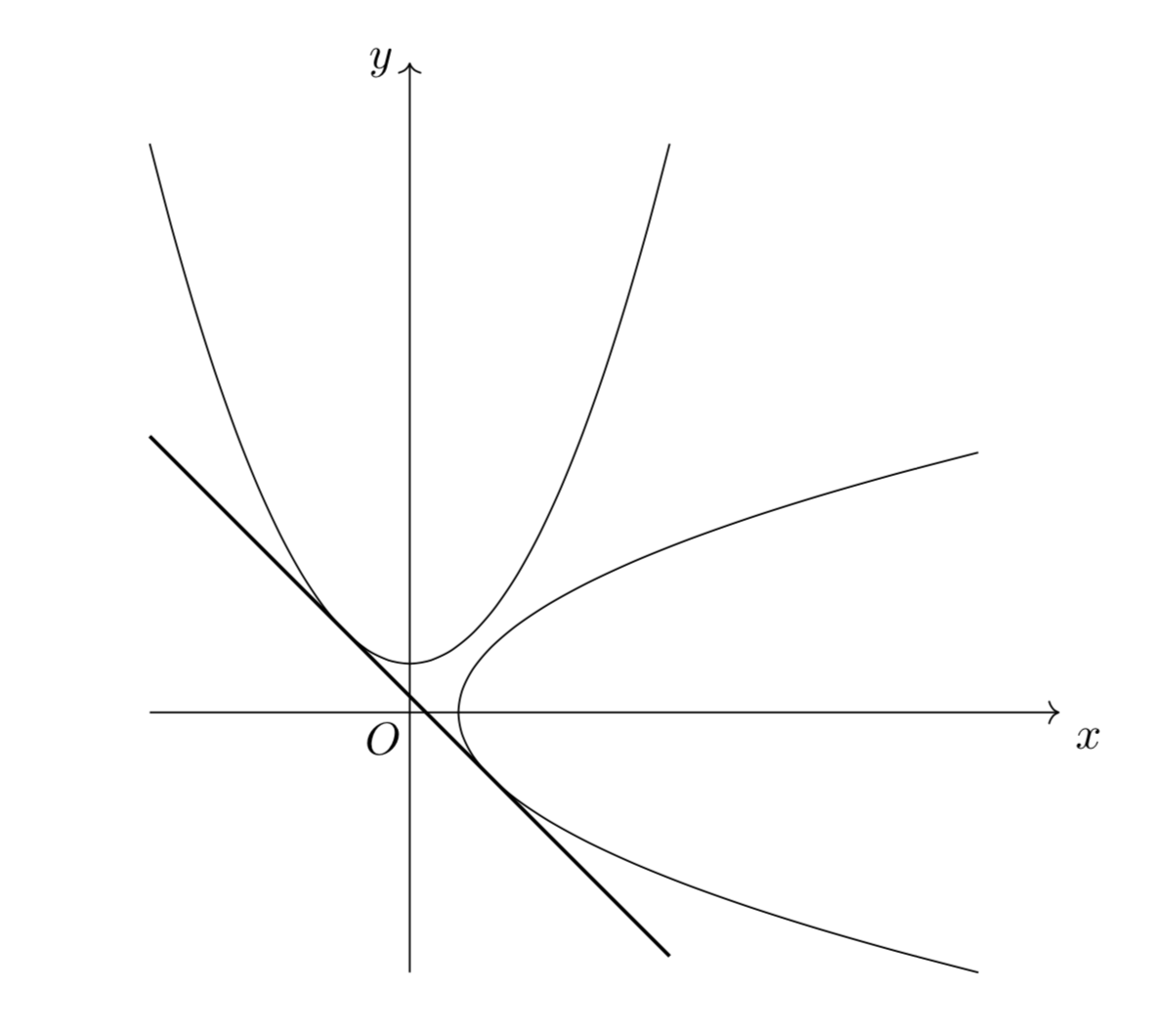
この存在を示し、接線の方程式をそれぞれ求めてあげればOKです。
傾きが$2$の共通接線が存在するとき、(1)の結果より、
\[k=\frac{2^2-2+1}{4\cdot2}=\frac{3}{8}\]
だと分かる。このとき、$a\ne 0$のもとで、
\[\frac{a^2-a+1}{4a}=\frac{3}{8}\Leftrightarrow a=\frac{1}{2},\,2\]
であるから、これをそれぞれ$b=\frac{-a^3+a^2-a+1}{4a}$に代入して、
\[(a,\,b)=\left(\frac{1}{2},\,\frac{5}{16}\right),\,\left(2,\,-\frac{5}{8}\right)\]
を満たすとき、共通接線になることがわかる。
また、$a=-1$のときについて考える。$y=-x+b$が共通接線だとすると、$y=x^2+\frac{3}{8}$から$y$を消去した2次方程式
\[x^2+x+\frac{3}{8}-b=0\]
が重解を持つので、
\[1-4\left(\frac{3}{8}-b\right)=0\Leftrightarrow b=\frac{1}{8}\]
が分かる。$y=-x+\frac{1}{8}$と$x=y^2+\frac{3}{8}$から$x$を消去した2次方程式
\[y^2+y+\frac{1}{4}=0\]
は重解として$y=-\frac{1}{2}$を持つので、$y=-x+\frac{1}{8}$も共通接線である。
以上の議論から、共通接線が3本存在することは示された。また、その共通接線の傾き$a$と$y$切片$b$は、
\[\boldsymbol{(a,\,b)=\left(\frac{1}{2},\,\frac{5}{16}\right),\,\left(2,\,-\frac{5}{8}\right),\,\left(-1,\,\frac{1}{8}\right)}\]
第六問
第六問は以下のような出題でした。

第六問の難易度分析
標準的な難易度の立体図形と体積に関する問題です。(2)だけで出題された場合には正答率がかなり低くなることが予想されますが、文字固定のしかたの誘導が付いているのでかなり解きやすくなっています。
ただ、(1)の誘導の意図を完璧に捉えるのは難しく、誘導にしっかり乗れればかなり短時間で正答を得ることができますが、そうでないと少し時間がかかってしまいます。
いずれにせよ、断面積を積分して体積を求めるという作業に慣れていれば完答は必ずできる問題です。
第六問(1)を解く上での考え方・ポイント
(2)では点$\mathrm{Q}$が平面$x=0$上を自由に動く場合について考えますが、それは難しいので、まずは$x=0$上の点である$(0,\,0,\,1)$に固定した場合にどうなるか考察する問題となっています。
点$\mathrm{P}$は線分$\mathrm{OQ}$を軸として回転し、回転半径は$\frac{\sqrt{3}}{2}$なので、$x$座標の取りうる値の範囲はすぐにわかります。
また、$\angle\mathrm{AOP}$については、計算によって動く範囲を求めるのは面倒ですが、図を描けば、点$\mathrm{A}$に点$\mathrm{P}$が最も近くなるときに角度が最小になり、最も遠くなるときに最大になることがわかるので、最大値と最小値を求めてからその間を連続的に変化することを述べてあげればよいでしょう。
点$\mathrm{Q}$が$(0,\,0,\,1)$にあるとき、点$\mathrm{P}$の動く範囲は下図の太線部になる。
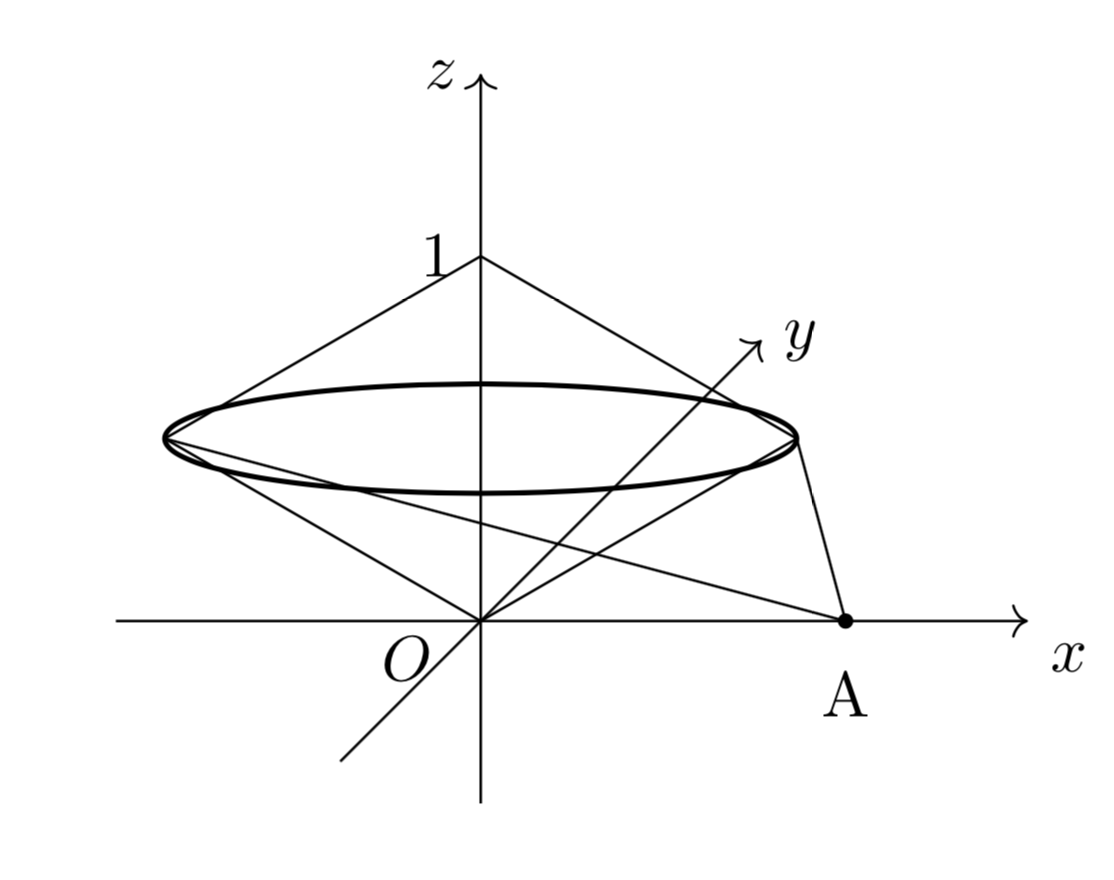
よって、点$\mathrm{P}$の$x$座標がとりうる値の範囲は、
\[\boldsymbol{-\frac{\sqrt{3}}{2}\leqq x\leqq\frac{\sqrt{3}}{2}}\]
また、上図より、$\angle\mathrm{AOP}$は、点$\mathrm{P}$が$\left(\frac{\sqrt{3}}{2},\,0,\,\frac{1}{2}\right)$にあるときに最小、$\left(-\frac{\sqrt{3}}{2},\,0,\,\frac{1}{2}\right)$にあるときに最大となり、その間を連続的に変化するので、求める$\theta$の範囲は、
\[\boldsymbol{30^{\circ}\leqq \theta \leqq 150^{\circ}}\]
第六問(2)を解く上での考え方・ポイント
誘導を意識しましょう。(1)の図から点$\mathrm{Q}$を固定したときに線分$\mathrm{OP}$が動いてできる図形は円錐であり、円錐を回転させてできる図形の体積を求めることになります。
そこで、まず思いつくのは円錐を$x$軸に垂直な平面によって切断して出てくる図形を$x$軸を中心に回転させた面積を$x$軸方向に積分するという解法です。しかし、そうすると、(1)で$\theta$の動く範囲を求めさせられた意味がよくわからなくなってしまいます…
$\theta$は点$\mathrm{P}$が自由に動ける範囲を表していることに気づきましょう。基本的には、点$\mathrm{P}$は$\mathrm{OP}=1$を満たしながら動くので、半径$1$の球の内部を動くことになりますが、$30^{\circ}\leqq \theta \leqq 150^{\circ}$をみたさない範囲は絶対に動くことができないのです。
そのため、点$\mathrm{P}$の動く範囲は、球の内側のうち、下図のような円錐の外側しか動けないことがわかります。
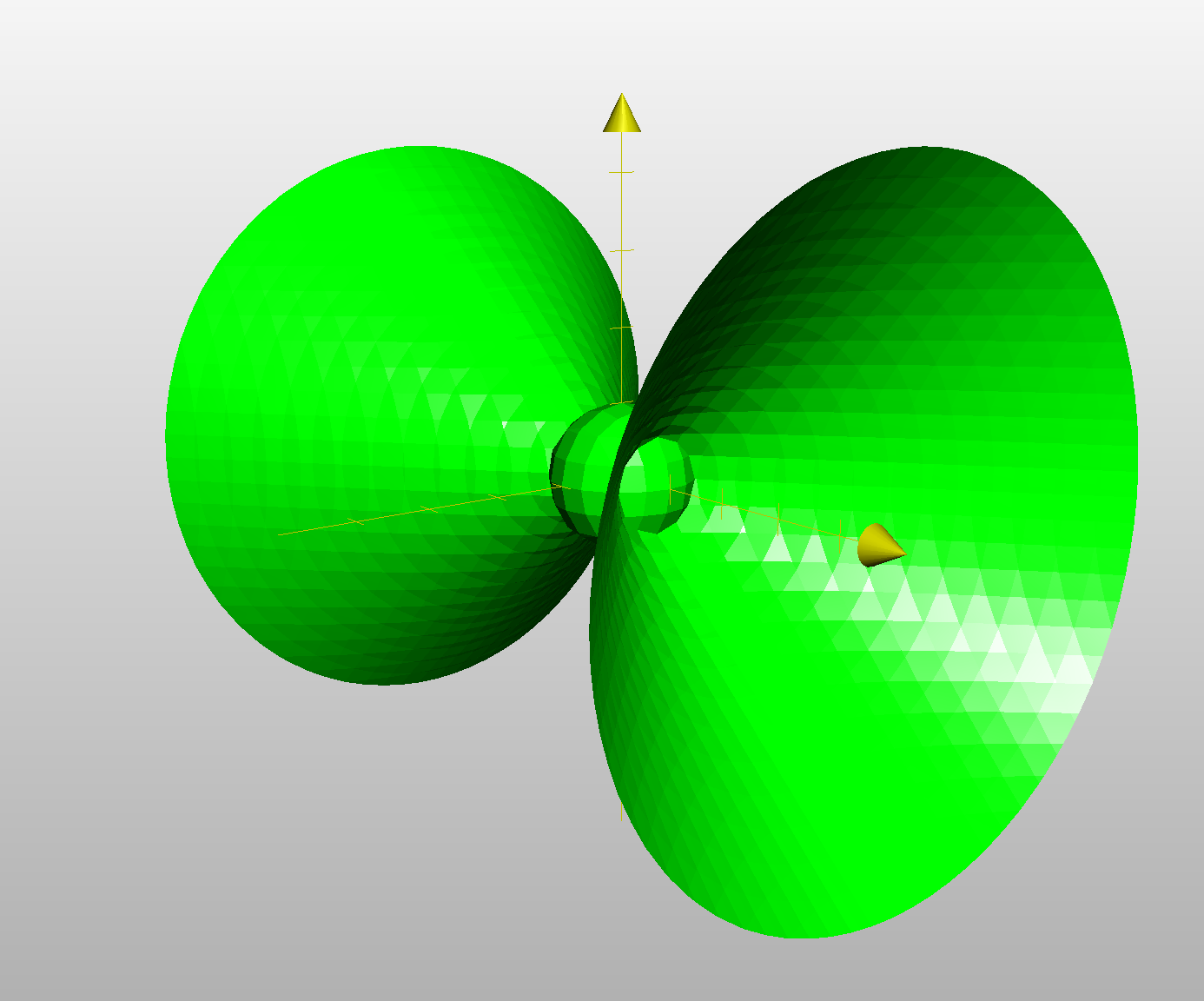
これを踏まえれば簡単に答えが出せますね。
$30^{\circ}\leqq \theta \leqq 150^{\circ}$より、$K$は、球$x^2+y^2+z^2=1$のうち、$\angle\mathrm{AOP}\leqq 30^{\circ}$、$\angle\mathrm{AOP}\geqq 150^{\circ}$を満たす範囲にある円錐面の外側の部分に等しい。
点$\mathrm{P}$の$x$座標がとりうる値の範囲が$-\frac{\sqrt{3}}{2}\leqq x\leqq\frac{\sqrt{3}}{2}$であることも考慮すると、求める体積は、球のうち$-\frac{\sqrt{3}}{2}\leqq x\leqq\frac{\sqrt{3}}{2}$の体積から、底面の半径が$\frac{1}{2}$で高さが$\frac{\sqrt{3}}{2}$の円錐2つ分の体積を除いたものになるので、
\[\begin{align*}&\int_{-\frac{\sqrt{3}}{2}}^{\frac{\sqrt{3}}{2}}\pi(1-x^2)dx-2\cdot \frac{\pi}{4}\cdot \frac{\sqrt{3}}{2}\cdot \frac{1}{3}\\=&\boldsymbol{\frac{2\sqrt{3}}{3}\pi}\end{align*}\]
(1)の誘導が見えにくく、この解法で解いた人は少ないかと思います。いつも通り、$x$軸に垂直な平面によって切断して出てくる図形を$x$軸を中心に回転させた面積を$x$軸方向に積分するという解法で解いてしまっても問題ないでしょう。
別解
点$\mathrm{Q}$が$(0,\,0,\,1)$にあるとき、線分$\mathrm{OP}$の動く範囲は(1)の図より円錐の側面になる。この方程式は、
\[x^2+y^2=3z^2(0\leqq z\leqq \frac{1}{2})\]
である。これと$x=k\left(-\frac{\sqrt{3}}{2}\leqq k\leqq\frac{\sqrt{3}}{2}\right)$の交線は、
\[3z^2-y^2=k^2(0\leqq z\leqq \frac{1}{2})\]
という双曲線になる。これを$x$軸を中心に回転させたときに通過する部分の面積を求めよう。
$x$軸に最も近い点は双曲線の頂点である$(y,z)=\left(0,\,\frac{k}{\sqrt{3}}\right)$であり、$x$軸から最も遠い点は、$(y,z)=\left(\pm\sqrt{\frac{3}{4}-k^2},\,\frac{1}{2}\right)$であるから、回転させた時に通過する部分の面積は、
\[\pi\left(1-k^2\right)-\pi\cdot\frac{k^2}{3}\]
であるから、求める体積は、これを$-\frac{\sqrt{3}}{2}\leqq k\leqq\frac{\sqrt{3}}{2}$の範囲で積分して、
\[\begin{align*}&\int_{-\frac{\sqrt{3}}{2}}^{\frac{\sqrt{3}}{2}}\pi\left(1-\frac{4}{3}k^2\right)dk\\=&2\pi\int_{0}^{\frac{\sqrt{3}}{2}}\left(1-\frac{4}{3}k^2\right)dk\\=&2\pi\left[k-\frac{4}{9}k^3\right]_{0}^{\frac{\sqrt{3}}{2}}\\=&\boldsymbol{\frac{2\sqrt{3}}{3}\pi}\end{align*}\]
誘導に気づけなくても、いつもどおりの方法で積分して求められる力は重要でしょう。
まとめ
近年稀に見る簡単な問題ばかりのセットであり、2017年は合格点が軒並み上がりました。
理三志望であれば、全問完答して110〜120点を狙いたい内容です。理一・理二志望であれば、白紙の問題は一つもない状態を作り、6問トータルでの失点を30〜40点にとどめ、80点〜90点を狙いたい内容です。
できなかった問題があれば基礎力の欠如の現れと言えるので、その問題に関連する分野の問題にたくさん触れると良いでしょう。





