※以下の解答・解説は当ブログのオリジナルのものであり東京大学が公表しているものではありません。
私がおすすめする過去問題集について説明した記事はこちら↓
第一問
第一問は以下のような出題でした。
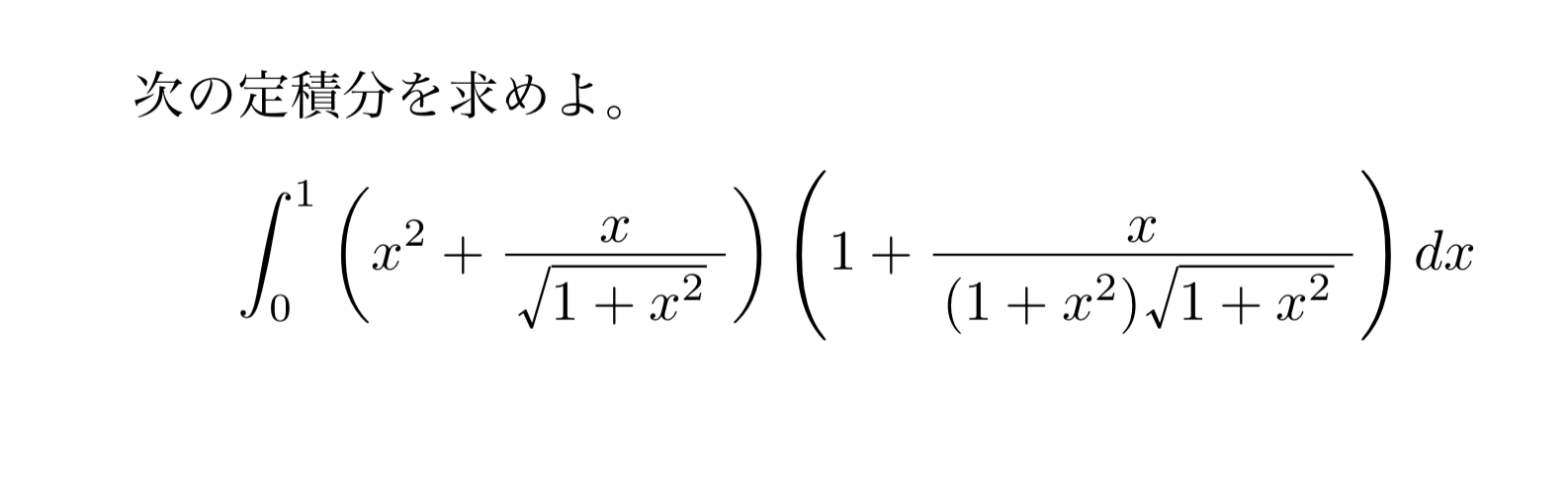
第一問の難易度分析
ただの定積分を求めさせる問題です。東大の数学の問題では初めてこのような形式の問題が出題されたのではないでしょうか。
非常に易しい問題で10〜15分程度で完答したいでしょう。
第一問を解く上での考え方・ポイント
ただただ展開して積分計算をしていくだけです。ただし、そのままうまく積分計算できないものは、$x=\tan \theta$と置換することになります。これは、積分における置換積分の鉄則のようなものですね。
積分で$a^2+x^2$の形が出てきたら$x=a\tan\theta$と置換する
シンプルに計算していけば簡単に答えは出るんですが、それではつまらないので、式の特徴を捉えて簡単に計算できる方法がないか考えてみましょう。
式を見てみると、右側のかっこの中身は、
\[x-\frac{1}{\sqrt{1+x^2}}\]
を微分した形になっているので、部分積分を狙えそうですよね。ただ、このままでは部分積分を実行しても計算は簡単になりません。この部分について、もし仮に真ん中の符号がプラスだったら、
\[x\left\{\frac{1}{2}\left(x+\frac{1}{\sqrt{1+x^2}}\right)^2\right\}^{\prime}\]
として、部分積分することでかなりきれいな形になりますよね。この発想から、被積分関数を
と変形すれば、部分積分によってきれいな形になります。第二項はそのまま積分できる関数ですよね。
これで計算が簡単になったかというと微妙なところですが、この方針で記述を書いてみると以下のようになります。
この第一項については、部分積分を用いて、
ここで、$x=\tan\theta$とすれば、
\[\frac{1}{2}\int_{0}^{1}\frac{1}{1+x^2}dx=\frac{1}{2}\int_{0}^{\frac{\pi}{4}}d\theta=\frac{\pi}{8}\]
である。
さらに、
\[\begin{align*}&2\int_{0}^{1}x\left(x+\frac{1}{\sqrt{1+x^2}}\right)dx\\=&2\left[\frac{x^3}{3}+\sqrt{1+x^2}\right]_{0}^{1}\\=&-\frac{4}{3}+2\sqrt{2}&\end{align*}\]
以上より、求める値は、
\[\begin{align*}&-\frac{19}{12}+\frac{\sqrt{2}}{2}+\frac{\pi}{8}+-\frac{4}{3}+2\sqrt{2}\\=&\boldsymbol{-\frac{35}{12}+\frac{5\sqrt{2}}{2}+\frac{\pi}{8}}\end{align*}\]
第二問
第二問は以下のような出題でした。

第二問の難易度分析
図形と絡めた最大最小問題です。難易度としては標準的でしょう。
自分でどこかの辺の長さを文字でおいてから、条件を数式化していくことになりますが、等式を用いて適切に文字消去を行っていくことによって、最終的に求めたい関数は1変数関数となります。(そのため文字固定などの議論は必要ありません。)
1変数までになったら、あとは微分によって簡単に最大値最小値が求まりますよね。
設定した文字の動く範囲がどうなるのかをしっかりと考えられれば難しくない問題でしょう。
第二問を解く上での考え方・ポイント
まず、どこの長さを文字でおくかに迷うかと思いますが、$\frac{\mathrm{DR}}{\mathrm{AQ}}$の変域について最終的に考えたいので、$\mathrm{AQ}=x,\,\mathrm{DR}=y$とおいてしまえばよいでしょう。
このときに、文字の変域も設定することを忘れてはいけません。ひとまずは、$0< x\leqq 1,\,0\leqq y\leq1$が必要ですね。($x=0$のときは三角形$\mathrm{APQ}$の面積が$\frac{1}{3}$になりえません。)
あとは面積についての条件が2つ与えられているので、それを$x,\,y$の条件として数式化していくことになります。その条件から、$\mathrm{AP}=\frac{2}{3x}$がわかりますが、$\mathrm{AP}$にも$0< \mathrm{AP}\leqq 1$の制約がつくので、
\[0< \frac{2}{3x}\leqq 1\Leftrightarrow \frac{2}{3}\leqq x\]
が得られます。この変域の条件を考え忘れていなければ、正しく最大値・最小値が求められます。
以下、解答例を示しておきます。
$\mathrm{AQ}=x,\,\mathrm{DR}=y$とおくと、$0< x\leqq 1,\,0\leqq y\leq1$である。
また、三角形$\mathrm{APQ}$の面積が$\frac{1}{3}$であることから、$\mathrm{AP}=\frac{2}{3x}$であるので、$0< \mathrm{AP}\leqq 1$より、
\[0<\frac{2}{3x}\leqq 1\]
である。$0< x\leqq 1$と合わせて、$\frac{2}{3}\leqq x\leqq 1$がわかる。
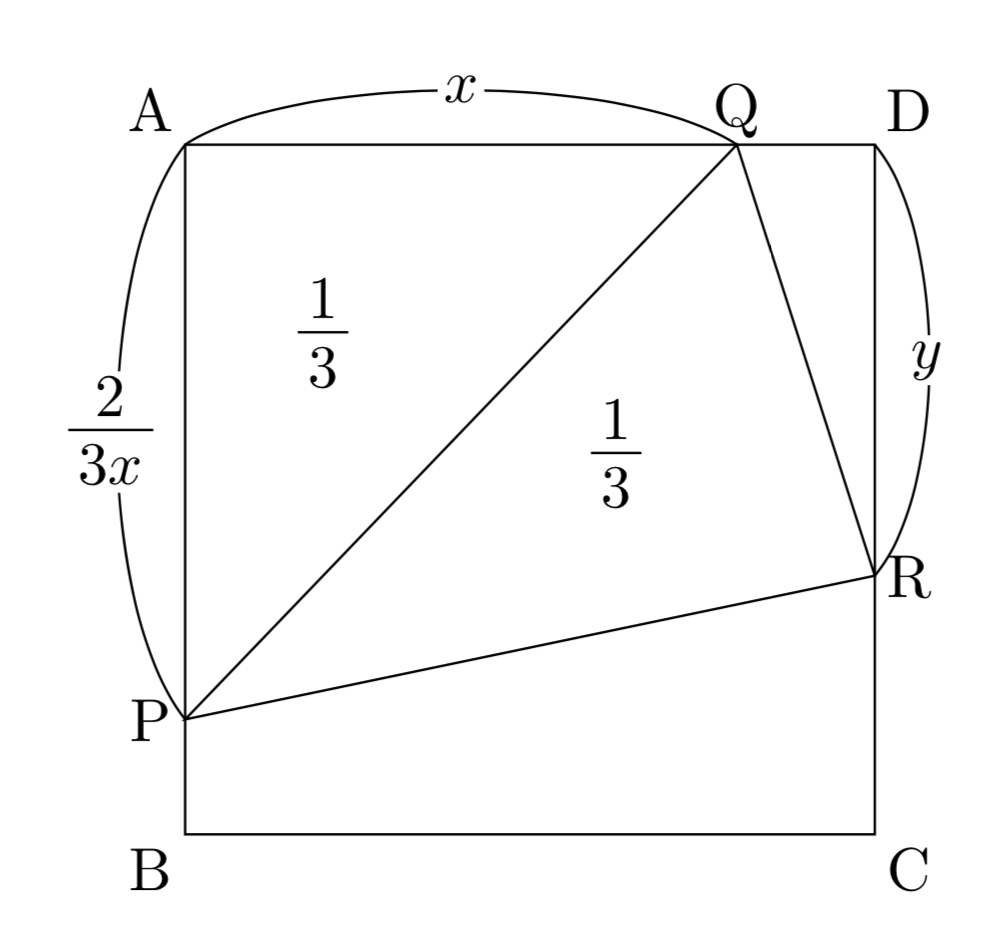
また、三角形$\mathrm{PQR}$の面積も$\frac{1}{3}$であることから、
\[\begin{align*}& \frac{1}{2}\left(\frac{2}{3x}+y\right)-\frac{1}{2}(1-x)y=\frac{2}{3}\\\Leftrightarrow &\frac{y}{x}=\frac{4}{3x^2}-\frac{2}{3x^3}\end{align*}\]
したがって、この右辺を$f(x)$とすれば、$\frac{2}{3}\leqq x\leqq 1$の範囲における$f(x)$の最大値・最小値を求めればよい。
\[f'(x)=\frac{6-8x}{3x^4}\]
であるから、増減表は以下のようになる。
\[\begin{array}{|c||c|c|c|c|c|} \hline x&\frac{2}{3}&\cdots&\frac{3}{4}&\cdots&1\\\hline f'(x)&&+&0&-&\\\hline
f(x)&\frac{3}{4}&\nearrow&\frac{64}{81}&\searrow&\frac{2}{3}\\\hline\end{array}\]
したがって、最大値$\boldsymbol{\frac{64}{81}}$、最小値$\boldsymbol{\frac{2}{3}}$
第三問
第三問は以下のような出題でした。

第三問の難易度分析
標準的な難易度の空間図形の問題です。空間図形を切り口で捉えるように丁寧な誘導がついていますが、ある程度は空間のイメージを持っていないと解きづらい問題になっているように思います。
(2)では、八角形である条件とは結局何なのか、という点について考えたいところです。
また、(3)では、やや長い問題文になっていますが、結局は$y\geqq 0,\,z\geqq 0$の範囲にある八角形の頂点がどれなのかを把握して、それらの$y$座標と$z$座標を知ることが課題です。
このように、「結局何を問われているのか」という点に注目することができれば完答できる内容の問題だったでしょう。
第三問(1)を解く上での考え方・ポイント
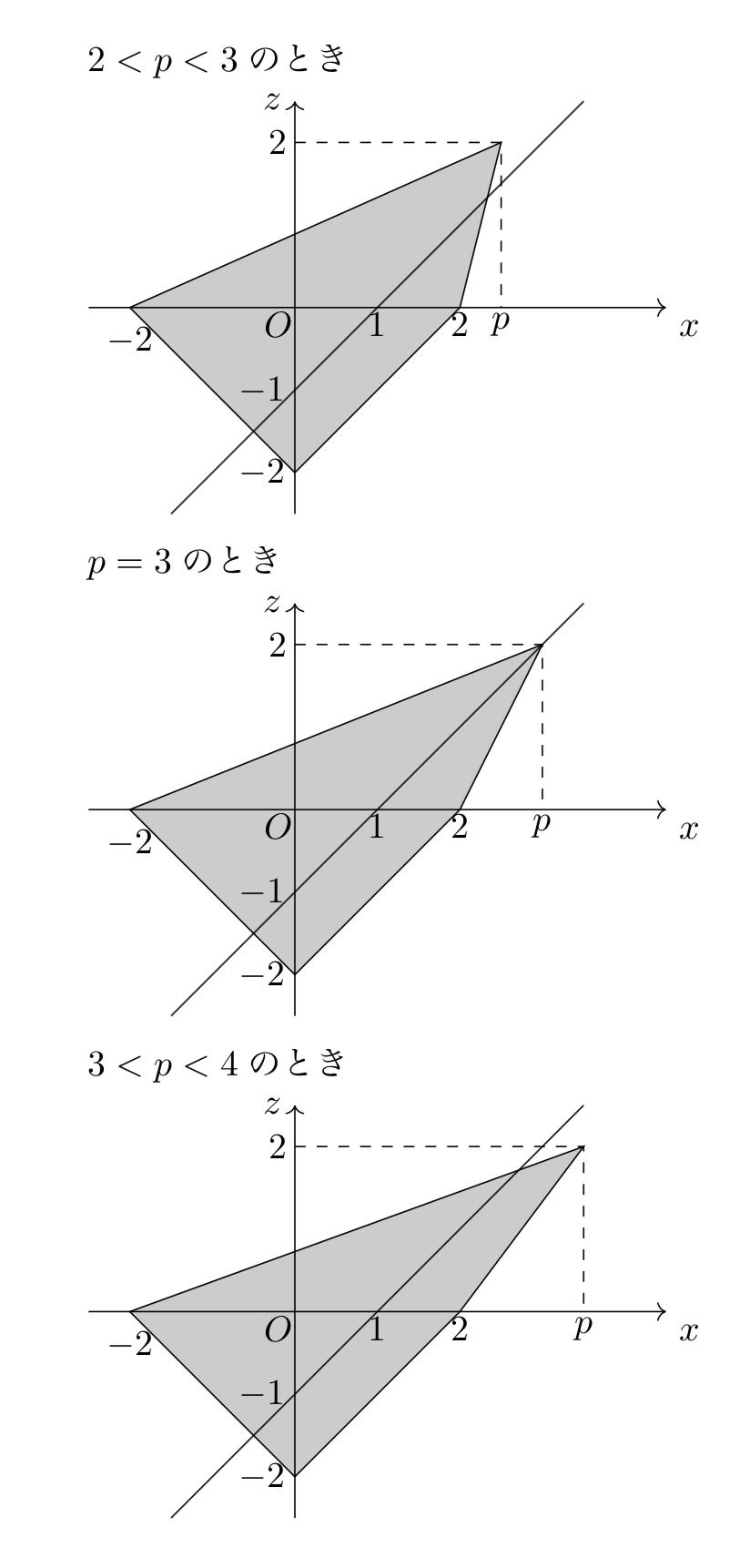
八面体$\mathrm{PABCDE}$を$y=0$で切断すると、四角形$\mathrm{PCEA}$が断面として出てくるのはすぐに分かると思います。
平面$\alpha$については、点$\mathrm{P}$、線分$\mathrm{MN}$の中点である$(1,\,0,\,0)$が$\alpha$上にも$y=0$上にもある点なので、切り口は$(1,\,0,\,0)$と点$\mathrm{P}$を結ぶ直線になります。
点$\mathrm{P}$の位置によって共有点を持つ部分は変化していくので、3通りの図を描いておく必要があります。
図を描くまでの記述はかなりあっさりしていて大丈夫でしょう。
八面体$\mathrm{PABCDE}$の切り口は四角形$\mathrm{PCEA}$である。また、線分$\mathrm{MN}$の中点である$(1,\,0,\,0)$は$\alpha$上にも$y=0$上にもある点より、平面$\alpha$の切り口は$(1,\,0,\,0)$と点$\mathrm{P}$を結ぶ直線になる。したがって、これらを$xz$平面上に図示すると下図のようになる。
第三問(2)を解く上での考え方・ポイント
(1)で図を描かされたのが大きなヒントになっています。図を見てみると、$p$の値によって、平面$\alpha$と四角形$\mathrm{PCEA}$の交わる部分が変化することに気が付きます。
具体的には、(1)の図で点$\mathrm{P}$が$\alpha$の切り口よりも右側に来たときには、線分$\mathrm{PC}$が$\alpha$と交わることがわかります。このとき、線分$\mathrm{PB}$と$\mathrm{PD}$も$\alpha$と交わることになりますよね。
すると、共有点の個数が8つになって、断面が八角形になります。これを記述すればよいでしょう。
$z\leqq 0$の部分について、八面体$\mathrm{PABCDE}$と平面$\alpha$は、線分$\mathrm{AB}$、$\mathrm{AD}$、$\mathrm{BE}$、$\mathrm{CE}$、$\mathrm{DE}$と交わるので、$\alpha$による切り口が八角形になるには、$z>0$において、八面体$\mathrm{PABCDE}$が平面$\alpha$と3つの辺で共有点を持てばよい。
(1)の図より、$xz$平面において、点$\mathrm{P}$が$z< x-1$の領域にあるとき、線分$\mathrm{PB}$、$\mathrm{PC}$、$\mathrm{PD}$の3つが$\alpha$と交わることになるから、求める$p$の条件は、
\[2<p-1かつ2<p<4\Leftrightarrow \boldsymbol{3<p<4}\]
第三問(3)を解く上での考え方・ポイント
結局、$y\geqq 0,\,z\geqq 0$の範囲にある八角形の頂点の座標を求めるのがやるべきことですね。少し立体図の想像が必要になりますが、この領域内にある八角形の頂点は、線分$\mathrm{AB}$、$\mathrm{PB}$、$\mathrm{PC}$と平面$\alpha$の交点です。
この3つの頂点の座標を求めて$yz$平面への射影を図示し、面積を求めるだけです。3点の座標を求めればいい、ということに気づけば難なく解ける問題でしょう。
最後の面積を求めるところでは、三角形2つに分割して計算するのが楽です。
以下、解答例を示しておきます。
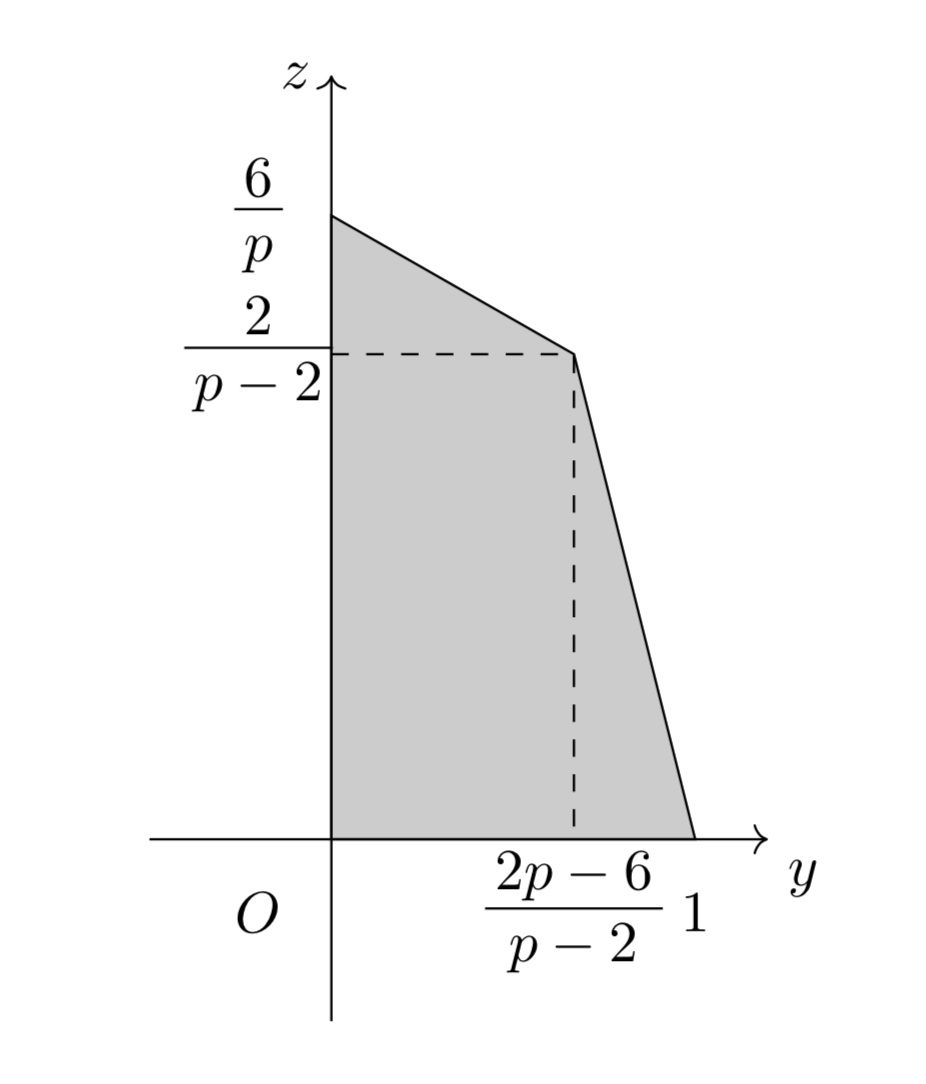
$\mathrm{PB}$、$\mathrm{PC}$と平面$\alpha$の交点をそれぞれ$\mathrm{F}$、$\mathrm{G}$と名付けると、切り口の八角形の頂点のうち、$y\geqq 0,\,z\geqq 0$の範囲にあるのは$\mathrm{M}$、$\mathrm{F}$、$\mathrm{G}$の3点。
まず、点$\mathrm{F}$について、線分$\mathrm{BF}$の$xz$平面への正射影は$z=\frac{2}{p}x(0\leqq x\leqq p)$であるから、これと直線$z=x-1$から$x$を消去して、
\[z=\frac{p}{2}z-1\Leftrightarrow z=\frac{2}{p-2}\]
よって、点$\mathrm{F}$は線分$\mathrm{BP}$を$\frac{2}{p-2}:2-\frac{2}{p-2}$に内分する点だとわかるので、点$\mathrm{F}$の$y$座標は、
\[2-\frac{2}{p-2}=\frac{2p-6}{p-2}\]
となる。
また、点$\mathrm{G}$について、線分$\mathrm{PC}$は$z=\frac{2}{p+2}(x+2)(-2\leqq x\leqq p)$であるから、これと直線$z=x-1$から$x$を消去して、
\[z=\frac{2}{p+2}(z+3)\Leftrightarrow z=\frac{6}{p}\]
したがって、3点$\mathrm{M}$、$\mathrm{F}$、$\mathrm{G}$の$yz$平面への正射影は以下の図のようになる。
したがって、求める面積は、
\[\begin{align*}&\frac{1}{2}\cdot1\cdot\frac{2}{p-2}+\frac{1}{2}\cdot\frac{6}{p}\cdot\frac{2p-6}{p-2}\\=&\boldsymbol{\frac{7p-18}{p(p-2)}}\end{align*}\]
第四問
第四問は以下のような出題でした。

第四問の難易度分析
易しい整数問題です。整数問題で平方数が絡んだ問題では法を4とした合同式を扱うことが多いという話を以下の記事でしていますが、そのあたりの知識があると(1)はかなりスムーズに解けるかと思います。
整数問題の解法については以下の記事にまとめています。
(2)は2通りの場合分けをすることになりますが、思考停止で法を4とした合同式だけを考えていると苦しい展開になります。冷静に今の状況を見て適切に方針を切り替えることを考えましょう。
第四問(1)を解く上での考え方・ポイント
「最大公約数」と言われれば、真っ先に思いつくのがユークリッドの互除法ですよね。今回の問題でも、「互除法だけで解決するかはわからないけど、課題を簡単にするために一度互除法を使おう」くらいの気持ちで互除法を試してみるべきです。
実行してみると、
\[5n^2+9=5(n^2+1)+4\]
となり、$d_n$は$n^2+1$と$4$の最大公約数に等しいことがわかります。ここで、整数問題で頻出の以下の事項を思い出しましょう。
平方数が出てくるときには4で割ったあまり・3で割ったあまりに注目することが多い!
今回は、$n^2$という平方数の形が出てきて、かつ、$4$で割ったあまりに注目することになっており、納得の展開となっていますね。
$n$が奇数のときは$4$で割ったときのあまりが$1$になり、偶数のときはあまりが$0$になることを述べてあげればよいでしょう。
以下、記述例になります。
ユークリッドの互除法を用いると、
\[5n^2+9=5(n^2+1)+4\]
であるから、$d_n$は$n^2+1$と$4$の最大公約数に等しいことがわかる。
ここで、ある整数$n$について、$n^2$を$4$で割ったあまりは$n$が奇数のとき$1$、$n$が偶数のとき$0$となるので、$n$が奇数のとき$n^2+1$は$4$で割って$2$余る数、$n$が偶数のとき$n^2+1$と$4$は互いに素である。したがって、
\[\left\{\begin{array}{l}\boldsymbol{d_n=1(nが偶数のとき)}\\\boldsymbol{d_n=2(nが奇数のとき)}\end{array}\right.\]
第四問(2)を解く上での考え方・ポイント
(1)が誘導になっていることを意識しましょう。$(n^2+1)(5n^2+9)$が平方数になるときは、$k,\,l$を互いに素でかつ、$d_n$とも互いに素な自然数として、
\[\left\{\begin{array}{l}n^2+1=d_nk^2\\5n^2+9=d_nl^2\end{array}\right.\]
と表せることと等しいですよね。これを満たすような$k,\,l$が存在しないことを$d_n=1,\,2$のそれぞれの場合で示せばよいわけです。
$d_n=1$のときは、
\[n^2+1=k^2\Leftrightarrow (k-n)(k+n)=1\]
と因数分解できて、これを満たすような自然数$k,\,n$の組がないことを示してあげればOKです。これは簡単ですね。
受験生が苦戦したと思われるのが$d_n=2$のときです。
このときは、
\[\left\{\begin{array}{l}n^2+1=2k^2\\5n^2+9=2l^2\end{array}\right.\]
となり、2式とも先ほどのように因数分解はできないので、別の解法を考えることになります。整数問題の解法は主に以下の3つでした。
整数問題の解法3パターン!
1.因数分解
2.合同式
3.範囲の絞り込み
平方数が出てきているので、合同式による解法を次に考えましょう。(1)で法を$4$とした合同式を考えますが、$n,\,k,\,l$がすべて$1$と合同であれば2式を満たしており、うまくいきません。
「他の解法を考えようかな…」となってしまいそうですが、ちょっと考えてみてください。合同式の法を$4$として考えたときは、$n^2+1\equiv 5n^2+9$が成り立つことから、せっかく2式あるのに1つしか条件を考えていないことになってしまいます。
実はこういうときには、合同式の法は$4$ではなく、$8$を選ぶとさらに細かく条件を考えることができます。
以上を踏まえて答案を書くと以下のようになります。
$(n^2+1)(5n^2+9)$が平方数であると仮定する。
(i)$d_n=1$のとき、$k,\,l$を互いに素な自然数として、
\[\left\{\begin{array}{l}n^2+1=k^2\\5n^2+9=l^2\end{array}\right.\]
が成立する。
\[n^2+1=k^2\Leftrightarrow (k-n)(k+n)=1\]
であり、$k,\,n$は自然数で$k+n>0$より、$k+n=1$かつ$k-n=1$が必要であるが、これを解くと$(k,\,n)=\left(\frac{1}{2},\,0\right)$となり、$k$が自然数でないので不適。
(ii)$d_n=2$のとき、$k,\,l$を奇数である互いに素な自然数として、
\[\left\{\begin{array}{l}n^2+1=2k^2\\5n^2+9=2l^2\end{array}\right.\]
が成立する。このとき、(1)より$n$は奇数であり、以下合同式の法を$8$とすれば、
\[n\equiv \pm 1\Rightarrow n^2\equiv 1\]
\[n\equiv \pm 3\Rightarrow n^2\equiv 1\]
が成立するので、$n^2\equiv 1$がわかる。$l$は奇数だから$l^2$についても同様のことが言えるので、$l^2\equiv 1$がわかる。よって、
\[5n^2+9\equiv 6\]
\[2l^2\equiv 2\]
が言えるので、$5n^2+9=2l^2$は成立しえず不適。
以上(i)(ii)より、$(n^2+1)(5n^2+9)$が平方数となる自然数$n$は存在しないことが示された。
別解
実質的には合同式の法を$8$として考えることと同じですが、2式を足し引きして出来た式の両辺を$2$で割ったあとに法を$4$とする合同式を考えてもうまくいきます。
((i)までは同じ)
(ii)$d_n=2$のとき、$k,\,l$を奇数である互いに素な自然数として、
\[\left\{\begin{array}{l}n^2+1=2k^2\\5n^2+9=2l^2\end{array}\right.\]
が成立する。2式を辺々足すと、
\[6n^2+10=2(k^2+l^2)\Leftrightarrow 3n^2+5=k^2+l^2\]
ここで、(1)より$n$は奇数であり、$3n^2+5$を$4$で割ったあまりは$0$となる。また、$k,\,l$は奇数であるから、$k^2+l^2$を$4$で割ったあまりは$2$となる。
よって、$3n^2+5=k^2+l^2$は成立しえず不適。
(以下略)
第五問
第五問は以下のような出題でした。

第五問の難易度分析
微分と極限が関わるやや難しい問題です。
問題の中では方程式の話になっていますが、与えられた方程式をグラフで考えることによって解答の方針がかなり立ちやすくなると思います。このように、代数と幾何の行き来は難関大の問題を解く上では非常に重要になるので、日頃から意識して練習しておくと良いでしょう。
(2)は(3)を解くための誘導になっていますが、$a$を求めるところまでしか役立たず、その先は少し考察が必要です。特に、$c$を求める議論は思いつかなかったという受験生が多いのではないかと予想します。
第五問(1)を解く上での考え方・ポイント
「ただ1つの実数解を持つ」ことを示すときには、「微分して単調性を示す」というのがあるあるな解法ですよね。しかしながら、今回は$(左辺)-(右辺)$をただただ微分すると、
\[(2n-1)x^{2n-2}+\sin x\]
となり、常に正であるとも常に負であるとも言えません。こういうときには、グラフの概形を描いて状況を整理するのが有効です。例として、$y=x^3$と$y=\cos x$のグラフを描くと以下の図のようになります。
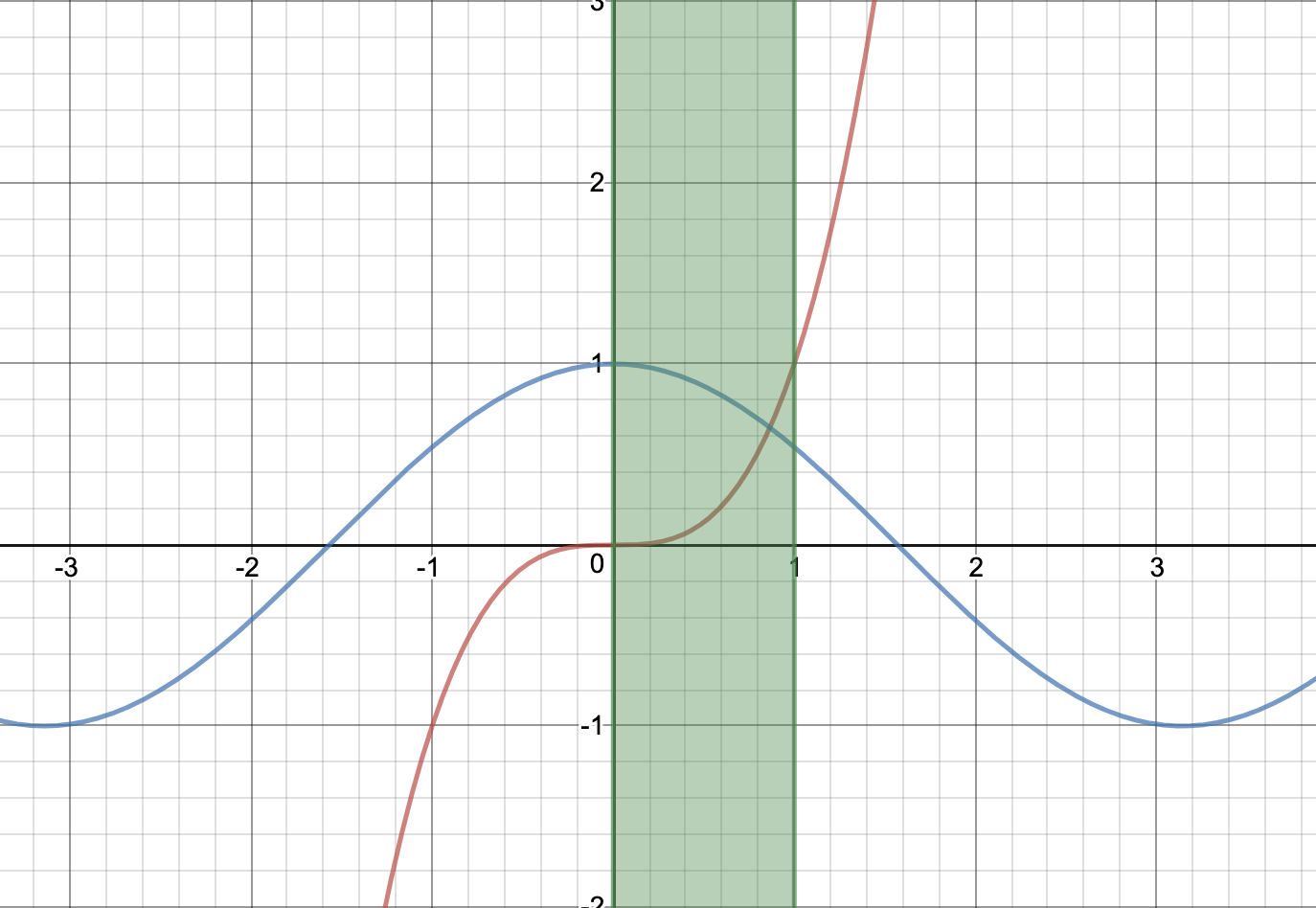
そうすると、$0\leqq x\leqq 1$の範囲で解を持っていて、$-1\leqq x<0$の範囲では正負が異なり、それ以外の範囲では$x^{2n-1}$の絶対値が$1$を超えてしまうので解を持ち得ないことが図からわかります。したがって、これらで場合分けをして議論してあげればよさそうです。
以下、解答例になります。
(i)$0\leqq x\leqq 1$のとき、
$f(x)=x^{2n-1}-\cos x$とすると、
\[f'(x)=(2n-1)x^{2n-2}+\sin x\]
$n\geqq 1$より、$(2n-1)x^{2n-2}\leqq 0$であり、$0\leqq x\leqq 1(< \pi)$より$\sin x\geqq 0$であるから、$f'(x)\geqq 0$がわかる。(ただし、$f'(x)=0$となるのは$x=0$のときのみ)
よって、この区間で$f(x)$は単調増加する。また、$f(0)=-1(<0)$、$f(1)=1-\cos 1>1-\cos 0=0$であるから、中間値の定理より、$f(x)=0$は$0<x<1$においてちょうど1つ実数解を持つ。
(ii)$|x|>1$のとき、
$|x^{2n-1}|>1$かつ$|\cos x|\leqq 1$より、与えられた方程式は実数解を持ちえない。
(iii)$-1\leqq x<0$のとき、
$x^{2n-1}<0$であり、$(-\frac{\pi}{2}<)-1\leqq x<0$において$\cos x>0$であるから、与えられた方程式は実数解を持ちえない。
以上より、$x^{2n-1}=\cos x$は$0<a_n<1$なるただ1つの実数解$a_n$を持つことが示された。
第五問(2)を解く上での考え方・ポイント
(1)が分かればこれは簡単ですね!サービス問題です。
$0<a_n<1(<\frac{\pi}{2})$であり、$\cos{x}$は$0<x<\frac{\pi}{2}$において単調減少するから、
\[\cos {a_n}>\cos 1\]
が成り立つことが示された。
第五問(3)を解く上での考え方・ポイント
(1)(2)までの議論をもとに、極限を3つ求めます。まず、$a$については、(1)の議論を踏まえると$1$が極限値になるのではないかと簡単に予想がつきます。
$a_n<1$はすでに示されているので、あとは$a_n$を下から評価してはさみうちの原理を用いてあげれば良さそうです。$a_n$より常に小さく、極限値が$1$になるようなものはどうやって見つければよいでしょうか?
そこで(2)が誘導になっていないかを考えます。
図を改めて描いてみると、$x^{2n-1}=\cos 1$となる$x$は常に$a_n$よりも左側に位置していることがわかりますよね。よって、$(\cos 1)^{\frac{1}{2n-1}}<a_n<1$としてはさみうちの原理を適用してあげればよさそうです!
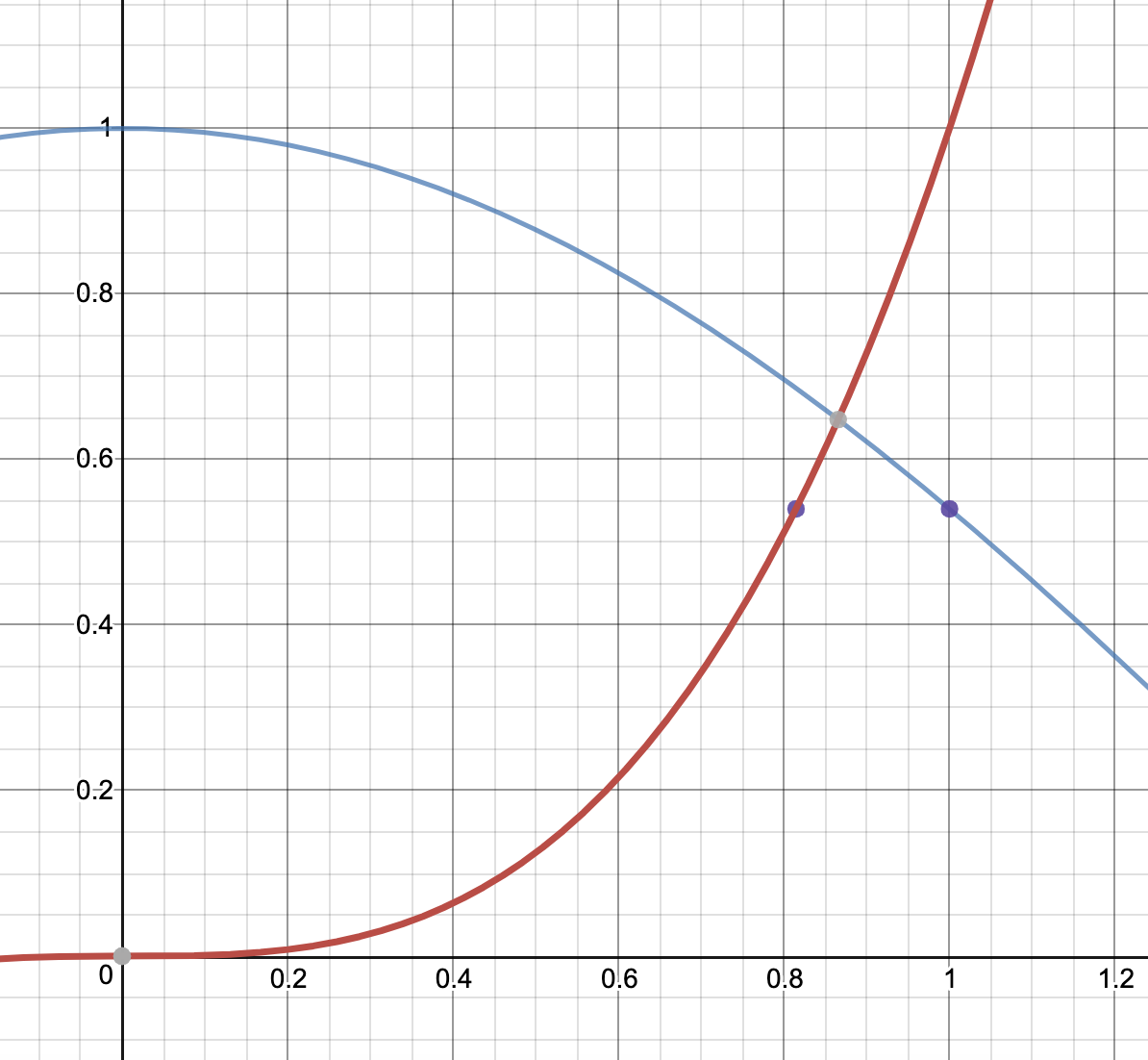
続いて、$b$については、$(\cos 1)^{\frac{1}{2n-1}}<a_n<1$を辺々$n$乗しても、左右で極限値が異なるのではさみうちの原理は使えません。そこで、そもそも$a_n$がどういう数だったかを思い出しましょう。
$a_n$は$x^{2n-1}=\cos x$の解なので、$a_n^n=(\cos a_n)^{\frac{n}{2n-1}}$と変形することができます。こうすれば、極限計算ができる形になりますよね。
こういうタイプの極限の話は2018年の夏の河合塾東大即応オープン模試第四問で出題されていました。

この問題の解説は以下になります。(興味のない方は読み飛ばしてもらって大丈夫です。)
難易度分析
標準的な関数と極限の問題です。
「ただ1つの共有点をもつ」ことを示すためには、微分によって関数の差の単調性を示すことが圧倒的に多いため、微分をする必要性が出てきそうです。
あとは、積分と極限です。共有点の座標が具体的には求まらず、不等式によって評価されているだけなので、積分値を不等式で評価するしかなく、はさみうちの定理を用いる展開が容易に想像がつきます。
ただ、意外とこの問題は難しく、誤答が相次いだのではないかと思います。
(1)を解く上での考え方・ポイント
接線とグラフの共有点を求める問題です。接線の式は、
\[l:y=2nx+2n\]
となるので、あとは$ C $の式と連立して$ y $を消去します。$ y $を消去すると、
\[x^{2n+1}-(2n+1)x-2n=0\]
となります。ここで、左辺を$ g(x) $とおいて微分すると、
\[g'(x)=(2n+1)x^{2n}-(2n+1)\]
となるので、$ x=1 $の前までは単調減少し、$ x=1 $のあとでは単調増加することがわかります。これと、$ g(1)=-4n(<0) $であることから、上の方程式は異なる実数解をちょうど2つもつことが分かり、そのうちの1つが$ x=-1 $なので証明完了ですね。
あとは、$ t_n<1+\sqrt{\frac{2}{n}} $を示すだけです。今までの議論から、これは、$ g\left(1+\sqrt{\frac{2}{n}}\right) $が正であることと同値ですよね。2項展開を考えれば、
という不等式が成り立つので、$ t_n<1+\sqrt{\frac{2}{n}} $であることも証明できました。
(2)を解く上での考え方・ポイント
(2)はあとは、積分してから極限計算をするだけです。$ \boldsymbol{t_n} $の具体的な値を求めることはできないので、はさみうちの定理の利用を考えます。
積分を実行すると、
となります。ここまでは誰でもたどり着けますが、極限計算で以下のような誤答が相次いだのではないかと思います。
【誤答例】
$ 1<t_n<1+\sqrt{\frac{2}{n}} $であるから、
したがって、はさみうちの定理から、\[\lim_{n\to \infty}\frac{S_n}{n}=4\]
この答案はどこが誤っているか分かりますか?
$ \frac{1}{n(2n+2)}\left(1-\left(1+\sqrt{\frac{2}{n}}\right)^{2n+2}\right)+4 $の極限を考える部分が違いますね。上の誤答例では、
\[\lim_{n \to \infty}\left(1+\sqrt{\frac{2}{n}}\right)^{2n+2}=1\]
だと考えてしまっていますが、これはいわゆる$ 1^{\infty} $の不定形の形ですね。この不定形は、ネイピア数$ e $の定義式の形に持っていって極限計算をするのでした。
$ 1^{\infty} $の形の不定形は、ネイピア数$ e $の定義式\[e=\lim_{x\to\infty}\left(1+\frac{1}{x}\right)^x\]
の形に変形して計算する。
よって、正しい極限計算は、
\[\begin{align*}&\lim_{n \to \infty}\left(1+\sqrt{\frac{2}{n}}\right)^{2n+2}\\=&\lim_{n \to \infty}\left(\left(1+\sqrt{\frac{2}{n}}\right)^{\sqrt{\frac{n}{2}}}\right)^{\sqrt{\frac{2(2n+2)^2}{n}}}\\=&\infty\end{align*}\]
となります。したがって、上の方針でははさみうちの定理が使えないわけです。
では、どのように解けばいいのでしょうか?
うまく極限が求まらない原因は、$ \boldsymbol{t_n^{2n+2}} $の項があることですよね。そもそも$ t_n $はどんな数だったかというと、$ g(x)=0 $の解でした。
そこで、$ \boldsymbol{t_n} $について成り立つ式$ \boldsymbol{g(t_n)=0} $を用いて次数下げをしてあげましょう。そうすることで、$ t_n $の指数が無限大に発散する事態を解消できそうです。
$ g(t_n)=0 $より、$ t_n^{2n+1}=2nt_n+2n $が成り立つので、これを代入して、
が成り立ちます。ここで、$ 1<t_n<1+\sqrt{\frac{2}{n}} $であるから、
したがって、はさみうちの定理より、
\[\lim_{n\to \infty}\frac{S_n}{n}=\boldsymbol{4}\]
が分かりました。
最後に$c$については、$\frac{a_nの関数-a_nの関数の極限値}{a_n-a_nの極限値}$の極限の形になっていることから、微分の定義式に非常に似た形をしていることに気づきたいところです。
微分の定義式
\[f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}\]
よって、数式を微分の定義式が使える形まで変形してあげれば極限が求まります。
以下、解答例になります。
(2)より、$\cos a_n>\cos 1$であるから、$x^{2n-1}$が単調増加関数であることを考慮すると、
\[\cos 1<a_n^{2n-1}\Leftrightarrow (\cos 1)^{\frac{1}{2n-1}}<a_n\]
が言える。よって、(1)の議論と合わせて
\[(\cos 1)^{\frac{1}{2n-1}}<a_n<1\]
が言える。ここで、$0<\cos 1<1$より、
\[\lim_{n\to \infty}(\cos 1)^{\frac{1}{2n-1}}=1\]
であるから、はさみうちの原理より、
\[a=\lim_{n\to \infty}a_n=\boldsymbol{1}\]
$a_n$は$x^{2n-1}=\cos x$の解であるから、
\[a_n^n=(\cos a_n)^{\frac{n}{2n-1}}\]
が成り立つ。よって、
\[b=\lim_{n\to \infty}(\cos a_n)^{\frac{1}{2}+\frac{1}{2(2n-1)}}=\boldsymbol{\sqrt{\cos 1}}\]
また、
\[\begin{align*}&\lim_{n\to \infty}\frac{a_n^n-b}{a_n-a}\\=&\lim_{n\to \infty}\frac{(\cos a_n)^{\frac{n}{2n-1}}-\sqrt{\cos 1}}{a_n-1}\\=&\lim_{n\to \infty}\frac{\sqrt{\cos a_n}-\sqrt{\cos 1}}{a_n-1}+\lim_{n\to \infty}\frac{(\cos a_n)^{\frac{n}{2n-1}}-\sqrt{\cos a_n}}{a_n-1}\\=&\lim_{n\to \infty}\frac{\sqrt{\cos a_n}-\sqrt{\cos 1}}{a_n-1}+\lim_{n\to \infty}\sqrt{\cos a_n}\cdot\frac{(\cos a_n)^{\frac{1}{2(2n-1)}}-1}{a_n-1}\\=&\lim_{n\to \infty}\frac{\sqrt{\cos a_n}-\sqrt{\cos 1}}{a_n-1}+\lim_{n\to \infty}\sqrt{\cos a_n}\cdot\frac{a_n^{\frac{1}{2}}-1}{a_n-1}\\=&\lim_{n\to \infty}\frac{\sqrt{\cos a_n}-\sqrt{\cos 1}}{a_n-1}+\lim_{n\to \infty}\sqrt{\cos a_n}\cdot\frac{1}{a_n^{\frac{1}{2}}+1}\end{align*}\]
であるから、$g(x)=\sqrt{\cos x}$とおくと、
\[\begin{align*}c=&g'(1)+\sqrt{\cos 1}\cdot\frac{1}{2}\\=&\boldsymbol{\frac{-\sin 1}{2\sqrt{\cos 1}}+\frac{1}{2}\sqrt{\cos 1}}\end{align*}\]
第六問
第六問は以下のような出題でした。
 お
お
第六問の難易度分析
やや難しい複素数平面に関する問題です。方程式の複素数解に関する問題にどれだけ触れたことがあるかで差がつく問題だったでしょう。
$\alpha,\,\beta,\,\gamma,\,\delta$は実数係数の方程式の解になっているので1つが虚数解であれば、それと共役な複素数解も含まれるというのが有名な話ですね。(この性質や示し方を知らないとかなり厳しい展開になります。)
また、議論がかなり細かく記述もしにくい内容になっているので、30分以上時間を使ってしまったという受験生が多いかと思います。
すべて解き切らずに部分点だけを狙って他の問題に移る判断が賢明でしょう。
第六問(1)を解く上での考え方・ポイント
実数係数の4次方程式の解に関する問題です。まず、「実数係数の$n$次方程式が複素数解を持つならばその共役複素数も解になる」という知識を持っていれば、その証明から入ることで、(i)すべてが実数解(ii)実数解2つ、複素数解2つ(iii)すべて複素数の3パターンしかないということが言えます。あとは、それぞれの場合において条件3をみたすことが必要という条件を考えればよさそうです。
以下、解答例になります。
まず、$z^4-2z^3-2az+b=0$がある複素数解$p$をもつとき、
\[p^4-2p^3-2ap+b=0\]
が成り立つ。両辺の共役複素数をとっても等式は成立するので、
\[\bar{p}^4-2\bar{p}^3-2\bar{a}\bar{p}+\bar{b}=0\]
$a,\,b$は実数であるから、$\bar{a}=a,\,\bar{b}=b$が成り立つので、
\[\bar{p}^4-2\bar{p}^3-2a\bar{p}+b=0\]
よって、$p$の共役複素数である$\bar{p}$も解になる。よって、$\alpha,\,\beta,\,\gamma,\,\delta$は
(i)すべて実数
(ii)2つは実数で、2つは互いに共役な複素数
(iii)互いに共役な複素数2組
の3パターンが考えられる。(i)のとき、$\alpha\beta+\gamma\delta$は実数なので条件3を満たさない。また、(iii)のとき、4解を$\alpha,\,\bar{\alpha},\,\beta,\,\bar{\beta}$とおいてよく、このとき、$\alpha\bar{\alpha}+\beta\bar{\beta}$、$\alpha\bar{\beta}+\beta\bar{\alpha}(=\alpha\bar{\beta}+\overline{(\alpha\bar{\beta})})$、$\alpha\beta+\bar{\alpha}\bar{\beta}$はすべて実数になるので、条件3に反する。
したがって、(ii)の場合であることが必要であるので、示された。
第六問(2)を解く上での考え方・ポイント
(1)より、4解は$s,\,t$を実数、$u$を複素数として$s,\,t,\,u,\,\bar{u}$とおくことができますね。このとき、条件3をみたすのはどのような組み合わせにしたときなのかをまず考えましょう。
$st+u\bar{u}$とすると、これは実数になってしまうので、$su+t\bar{u}$のときだとわかります。
$u=x+yi$とおけば、この実部が$0$になる条件は、
\[(s+t)x=0\]
であるので、$s=-t$または$x=0$のときです。あとはそれぞれの場合について調べれば解決しそうです!
以下、解答例です。
(1)より、4解は$s,\,t$を実数、$u$を複素数として$s,\,t,\,u,\,\bar{u}$とおきなおすことができる。条件3について、$st+u\bar{u}$は実数になることから、
\[su+t\bar{u}\]
が純虚数になることが条件3と同値である。ここで、$x,\,y$を実数として$u=x+yi(y\ne 0)$とおくと、純虚数になる条件は、
\[(s+t)x=0かつ(s-t)y\ne 0\]
である。ただし、$y\ne 0$、条件1より$s\ne t$であるから$(s-t)y\ne 0$は常に満たされる。
(i)$s+t=0$のとき、$t=-s$であるから、$z^4-2z^3-2az+b$は、
\[z^4-2z^3-2az+b=(z^2-s^2)(z-u)(z-\bar{u})\]
と因数分解できる。
であるから、係数を比較して、
\[\left\{\begin{array}{l}2x=2\\x^2+y^2-s^2=0\\2xs^2=-2a\\-(x^2+y^2)s^2=b\end{array}\right.\]
第一式より$x=1$であり、これと第三式から、
\[s^2=-a\]
$s$は$s\ne t$より$0$でない実数であるから$a<0$である。また、これらと第二式より、
\[1+y^2+a=0\Leftrightarrow y^2=-a-1\]
$y$は$0$でない実数であるから$a<-1$である。さらに、第四式に代入して、
\[b=-a^2\]
よって、$b=-a^2(a<-1)$である。
(ii)$x=0$のとき、$z^4-2z^3-2az+b$は、
\[z^4-2z^3-2az+b=(z-s)(z-t)(z^2+y^2)\]
と因数分解できる。
であるから、係数を比較して、
\[\left\{\begin{array}{l}s+t=2\\st+y^2=0\\(s+t)y^2=2a\\sty^2=b\end{array}\right.\]
が成り立つ。第一式と第三式から、
\[2y^2=2a\Leftrightarrow y^2=a\]
が成り立つ。$y$は$0$でない実数であるから、$a>0$が必要で、このもとで、$y=\pm\sqrt{a}$が言える。これと第二式より、
\[st=-a\]
がわかる。また、$s+t=2,\,st=-a$であるから、$s,\,t$は2次方程式$x^2-2-a=0$の2解で、$a>0$も考慮すると、$s,\,t$は、
\[1\pm\sqrt{1+a}\]
である。このとき、$a>0$より、$s\ne t$は常に満たされる。
これらを第四式に代入すると、
\[b=-a^2\]
よって、$b=-a^2(a>0)$である。
以上より、
\[\boldsymbol{b=-a^2(a<-1,\,0<a)}\]
第六問(3)を解く上での考え方・ポイント
ボーナス問題とも言える簡単な軌跡の問題です。
ここまでの議論では$s,\,t,\,u,\,\bar{u}$と$\alpha,\,\beta,\,\gamma,\,\delta$との対応を考えずに議論してきましたが、$\alpha+\beta$の動く範囲を考える上ではどういう対応関係があるかを考える必要があります。
$st+u\bar{u}$という組み合わせでなければ条件3はみたされるので、$\alpha+\beta$は4解のうち実数解と複素数解の和になります。あとは、これの軌跡を求めるだけです!ただし、軌跡を求めるときの注意点として、
軌跡を求めるときには、通らない点がないか気をつけよ
がありましたね!同値性に注意しながら変形していくことに気をつければよいだけなんですが、変形する際に出てきた場合分けなどの条件をすべて軌跡に反映させることを忘れないようにしましょう。
また、2つ出てくる場合分けは実は全く同じ軌跡を表していることにも気づきたいところです。
以下、解答例を示しておきます。
$s,\,t,\,u,\,\bar{u}$について、$st+u\bar{u}$以外の組み合わせであれば条件3はみたすので、対称性も考慮すると、
\[\alpha+\beta=s+u\]
としてよい。
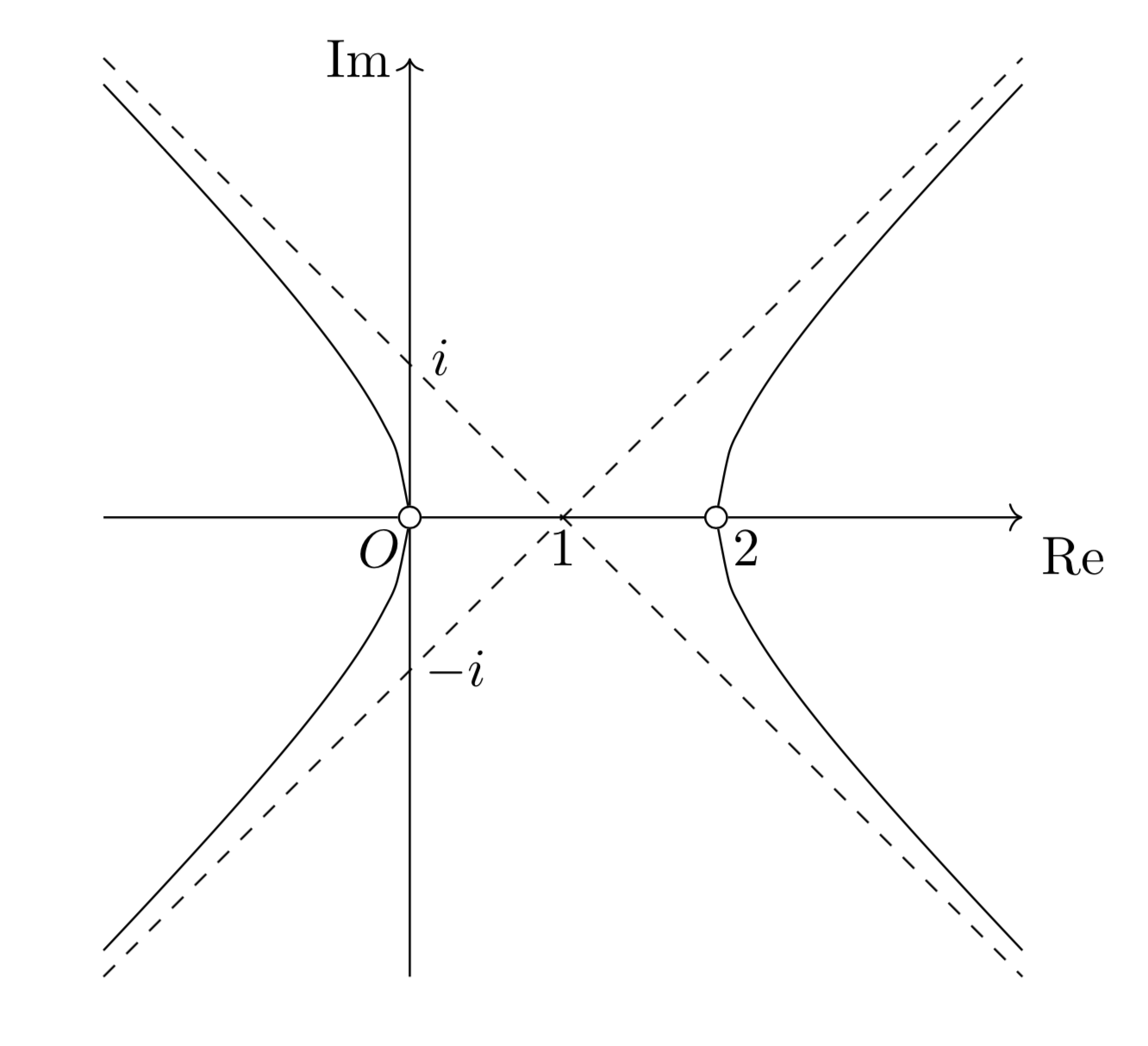
$a<-1$のとき、$s+u=\pm\sqrt{-a}+1+\pm\sqrt{-a-1}i(複合任意)$であり、$a>0$のとき、$s+t=1\pm\sqrt{1+a}\pm\sqrt{a}i(複合任意)$である。
ここで、前者について、$q=-a-1$と置き換えると$q>0$かつ$s+t=1\pm\sqrt{1+q}\pm\sqrt{q}i(複合任意)$となるので、後者と全く同じ範囲を表すことがわかる。
よって、$a>0$のもとでの$1\pm\sqrt{1+a}\pm\sqrt{a}i(複合任意)$の動く範囲を求めればよいとわかる。
$Y=\pm\sqrt{a}$とおくと、$y$は$0$でないすべての実数をとることができて、$X=1\pm\sqrt{1+a}$とすれば、
\[\begin{align*}&X=1\pm\sqrt{1+Y^2}\\\Leftrightarrow &X-1=\pm\sqrt{1+Y^2}\\\Leftrightarrow &(X-1)^2=1+Y^2\\\Leftrightarrow &(X-1)^2-Y^2=1\end{align*}\]
したがって、$Y\ne 0$に注意して、$\alpha+\beta$のとりうる値の範囲は下図の双曲線(ただし、白丸を含まない)。
まとめ
2017年や2018年はかなり易しい年だったため、難しいと感じた受験生が多いかと思いますが、最近の10年間の傾向からすると依然として易しい内容でしょう。
理三志望であれば、第五問、第六問を10点ずつ取って、その他の問題で失点を10点程度に抑えて90点くらいを狙いたい内容です。理一・理二志望であれば、第六問は0点でもよく、第五問、第六問以外の問題で失点を20点程度にとどめ70点くらいを狙いたい内容です。





