確率漸化式とは?
確率を求める過程で数列の漸化式が出てくるもの
確率漸化式とは、確率を求める上で出てくる、数列の分野で習う漸化式のことを指します。確率漸化式の問題では、確率と数列の2分野にまたがった出題をすることができるため、数学の総合力を問いやすく、大学受験ではよく出題されます。
受験生にとっては、確率と数列をどちらもしっかりと理解していないと解けない問題であるため、躓きやすい分野だと言えます。
数ⅠAⅡBの範囲で解けるので文系でも頻出
確率は数ⅠAの範囲、漸化式は数ⅡBの範囲で習うので、確率漸化式は文系や理系に関わらず入試問題で出されます。理系の場合には、求めた確率の極限値を問われることもしばしばあります。
この記事で扱う問題は1つ目は理系で出題された非常に簡単な問題、2つ目は文系でも出題された問題なので、文系の受験生にも必ず習得してほしい問題です。
東大の入試問題の良問を解いて確率漸化式を学ぼう
参考書の中で確率漸化式の問題を探して解いていくのは非効率的です。
この記事では、東大で過去に出題された入試問題の良問を軸にして、確率漸化式の習得を目指します。
以下がその問題です。ある程度確率漸化式について学んでいるという人はこれらの問題を実際に解いてみましょう。
問題1(正四面体と確率漸化式)
平面上に正四面体が置いてある。平面と接している面の3辺のうち、ひとつを任意に選び、これを軸として正四面体をたおす。$n$回の操作の後に、最初に平面と接していた面が再び平面と接する確率を求めよ。(1991年度東大理系第1問)
問題2(正三角形の9個の部屋と確率漸化式)
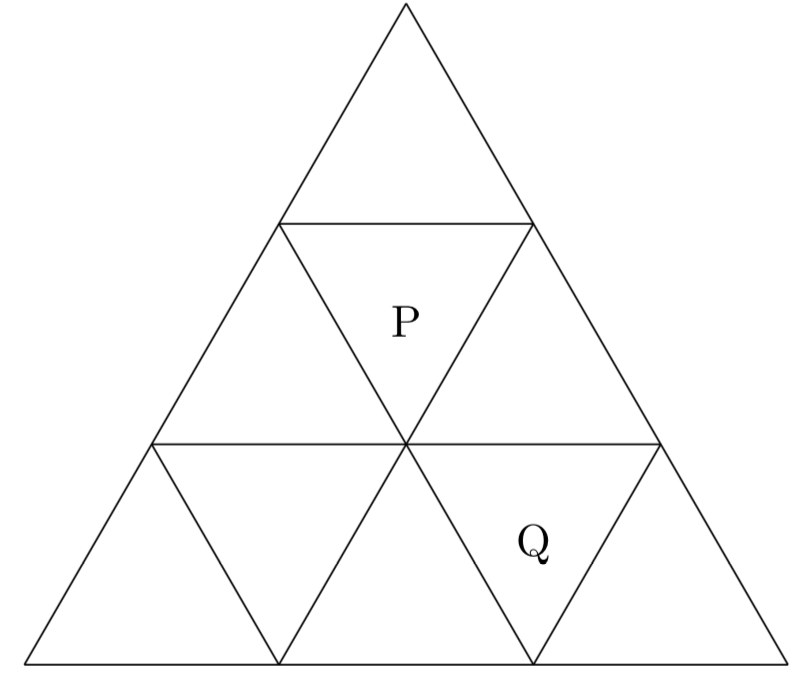
図のように、正三角形を9つの部屋に辺で区切り、部屋$\mathrm{P}$、$\mathrm{Q}$を定める。1つの球が部屋$\mathrm{P}$を出発し、1秒ごとに、そのまま部屋にとどまることなく、辺を共有する隣の部屋に等確率で移動する。球が$n$秒後に部屋$\mathrm{Q}$にいる確率を求めよ。(2012年東大文系第3問、理系第2問)
確率漸化式の解き方は?
まだ確率漸化式についての理解が浅いという人は、これから確率漸化式の解き方について説明していくので、それを元にして、上の例題を考えてみましょう!
n回の操作後の確率を数列として文字で置く
まずは、確率を数列として文字で置くという作業が必要です。これはすでに問題文中で定められていることも多いですが、上の問題1や問題2では定められていないので自分で文字で置く必要があります。
例えば問題1であれば、「最初に平面と接していた面が$n$回の操作後に平面と接している確率を$p_n$とおく」などの作業が必要になります。
遷移図(推移図)をまず描く
文字を置いたあとは、$\boldsymbol{n}$回目の操作のあとの確率と$\boldsymbol{n+1}$回目の操作のあとの確率がどのような関係にあるのかを表す遷移図(推移図)を描きます。
言葉で説明しても上手く伝わらないので、以下で例を挙げてみます。
$n$回の操作後、ある状態Aである確率を$p_n$と表すとします。そして、状態A以外の状態をBと名付けます。すべての状態の確率の和が$1$になることから、このとき状態Bである確率は、$1-p_n$ですね。
「状態Aであるときに、次の操作で再び状態Aとなる確率が$\frac{1}{3}$、状態Bであるときに、次の操作で再び状態Bとなる確率が$\frac{1}{3}$、状態Aであるときに、次の操作で状態Bとなる確率が$\frac{2}{3}$、状態Bであるときに、次の操作で状態Aとなる確率が$\frac{2}{3}$」
ということがわかっているとき、遷移図は以下のように描きます。
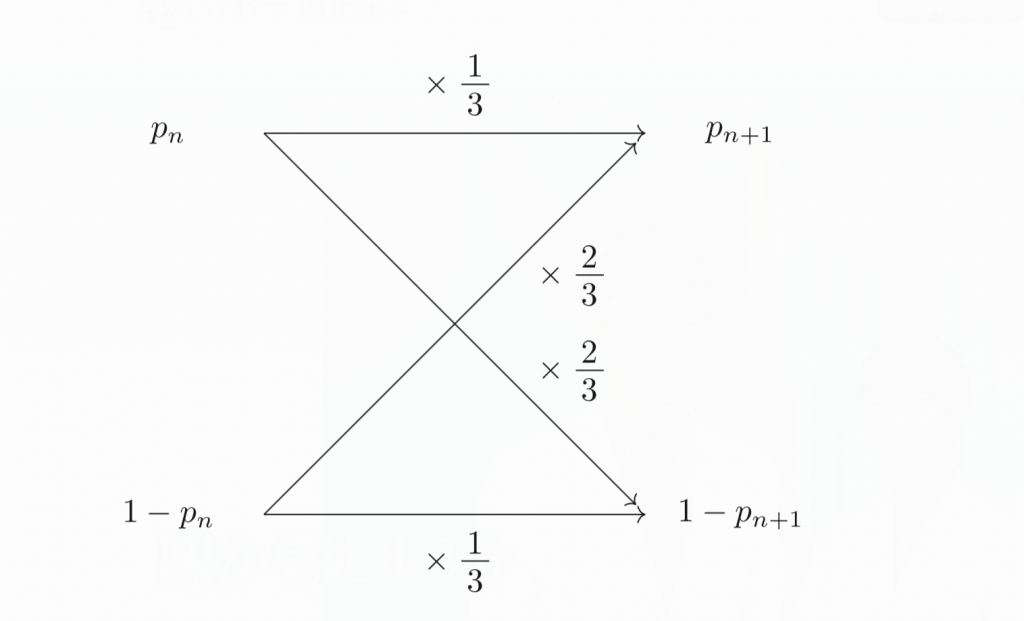
すなわち、遷移図とは毎回の操作によって確率がどのように分配されていくのかを表した図だということです。
遷移図を元に漸化式を立てて解く
遷移図が描けたら、それを元に漸化式を立てます。上の遷移図からは、
\[p_{n+1}=\frac{1}{3}p_n+\frac{2}{3}(1-p_n)\]
という漸化式を立てることができますね。
あとは、漸化式を解くだけです。漸化式を解く際には初項を求める必要があるので、必要に応じて適当な確率計算をして初項を求める必要があります。
漸化式の解き方がまだあやふやだという人はこちらの記事で漸化式の解き方を学んでくださいね。
確率漸化式を解く時の5つのポイント・コツ
確率漸化式を解く流れは上で説明した通りですが、確率漸化式を解くにはいくつかのポイントがあります。また、ちょっとしたコツを知っておくだけで計算量を減らすことができて、結果的に計算ミスの防止に繋がります。
それらのポイントやコツについて説明していきたいと思います。
対称性・偶奇性に注目して文字の数を減らす
確率漸化式を解く上で最も重要なポイントは、文字の数をなるべく減らしておくということです。
例えば、上で挙げた問題1では、正四面体の4面のうち、初めに平面に接していた平面だけを特別視しており、それ以外の3面は対称です。
したがって、対称性に着目すれば、4面を別々に見るのではなく、最初に平面に接していた平面が$n$回の操作のあとに平面に接している確率を$p_n$、それ以外の3面のどれかが平面に接している確率を$q_n$と置いたりすれば十分そうです。つまり、最大でも2文字置けば十分ということですね。
偶奇性というのは、偶数回の操作を行った時、奇数回の操作を行った時をそれぞれ別個に考えると、推移の状況が単純化されるというものです。
例えば、上で挙げた問題2では、奇数秒後には絶対に$\mathrm{Q}$の部屋にはいないことが容易にわかります。そのため、偶数秒後と奇数秒後を分けて考えることによって、存在しうる部屋の数が限定されて、文字の数を減らすことができそうです。
すべての確率を足すと1になる条件を忘れないようにする
これはだいぶ初歩的なことなんですが、確率をすべて足し合わせた時にその確率は1になるという非常に当たり前の条件を忘れてしまって行き詰まるということが、確率漸化式を習いたての人にはしばしば起こるようです。
例えば、問題1において、最初に平面に接していた平面が$n$回の操作のあとに平面に接している確率を$p_n$、それ以外の3面のどれかが平面に接している確率を$q_n$と置いたとすれば、
\[p_n+q_n=1\]
という条件式があることを忘れてはいけないということですね。
そもそもこれを意識していれば、$\boldsymbol{q_n}$という新しい文字を置く必要性すらなく、$\boldsymbol{p_n}$と$\boldsymbol{1-p_n}$という2つの確率について考えていけばよいわけです。
3種類以上の数列の連立漸化式を解くことはほとんどない
対称性と偶奇性、確率を足すと1になるという条件などなどをすべて考慮していけば、連立漸化式を解く状況になったとしても、3種類以上の数列が含まれた連立漸化式を解くことはほとんどありません。(以前は「絶対にない」と断言していたのですが、2018年度東工大第5問で4種類の数列の連立漸化式を解かせる問題が出題されているとの情報をいただきました。)
つまり、
\[\left\{\begin{array}{l}a_{n+1}=pa_n+qb_n\\b_{n+1}=ra_n+sb_n\end{array}\right.\]
という形の連立漸化式を解く状況にはなりえますが、他の数列$c_n$が含まれているような状況には、ほとんどならないということです。
これは、高校の教科書で漸化式の解き方を習う上で3文字以上の連立漸化式を扱わないことが理由だと思われます。
n=0を考えれば初項を求めるのに計算要らずのことが多い
漸化式を解く時に、初項というとついつい$n=1$のときを考えてしまいがちなんですが、これを求めるには簡単ではあるものの確率の計算が必要です。
そこで、$\boldsymbol{n=0}$の時を初項として選ぶことによって、初項を計算せずに求められるというちょっとしたコツがあります。
例えば、上で挙げた問題2を解く上では、偶奇による場合分けが必要なので、$n=2$のときに$\mathrm{Q}$にいる確率を求める必要があるように思ってしまいがちなんですが、 $n=0$のときに、確率が$0$であるという当たり前の事実から初項として$n=0$のときを選べば計算要らずです。
n→∞の極限が正しいかで検算ができるときがある
答えを求められたあとに、この答えって合ってるのかなと気になることがありますよね。確率漸化式も結局は数列の問題なので、$n=1,\,2,\,3$のときなどを調べて、求めた式に代入したものと確率が一致しているか確かめれば検算になりますが、 $\boldsymbol{n\rightarrow\infty}$のときの極限計算によっても検算をすることができます。
例えば問題1であれば、$n\rightarrow\infty$のときの確率はどうなってるでしょうか?何度も何度も転がしていけば、結局正四面体のサイコロを振ってる状況と変わらないですよね。ということは、確率の極限値は$\frac{1}{4}$になることが容易に想像がつきます。
このように、極限値の推定ができるとき、その極限値と一致しているか確かめることによって、検算の一助になるわけです。
以下で、東大の過去問2題を例にして確率漸化式の解き方について学んでいきます。
確率漸化式は、分野横断型の問題であるがゆえに、数学Ⅰ、数学Bなどのように分かれた参考書、問題集では扱われていないことがほとんどです。
東大の過去問では難しすぎる!もっと色んな問題を解きたい!という方には、「解法の探求・確率」という参考書がおすすめです。
確率漸化式はもちろん、確率全般について網羅的に学べる良書です。
問題1(正四面体と確率漸化式)の解答・解説
問題1の解答と解説を始めていきましょう!数学は適切な指針を立てられるようになることが最も重要ですから、まず解説を書いてから、そのあと私が作ってみた模範解答を載せようと思います。
問題1を解く上でのポイント
まずは、文字設定を行っていきましょう。
求めたい確率を文字で置いておきたいので、$n$回の操作のあとに最初に平面に接していた面が平面に接している確率を$p_n$と置いてあげればよいでしょう。
説明を短くするために、以下では、最初に接していた面をAと呼ぶことにします。
また、正四面体なので、対称性に着目すると良さそうです。A以外の3面はすべて対称なので、それぞれについて確率を文字で置くのではなく、「$n$回の操作のあとにA以外の3面が平面に接している確率」を置いてあげれば良さそうです。
さらに、4面の確率をすべて足し合わせると$\boldsymbol{1}$になることも考慮すると、その確率は$\boldsymbol{1-p_n}$となるので、新しい文字を置く必要すらありません。
さて、文字設定ができたら、次は遷移図を書きましょう。
Aが平面に接しているときには、次の操作で必ず他の3面が接する状態に遷移し、A以外の3面が接しているときには、次の操作で$\frac{1}{3}$の確率でAが接する状態に遷移し、$\frac{2}{3}$の確率でそのままの状況になりますよね。
したがって、遷移図は以下のようになります。
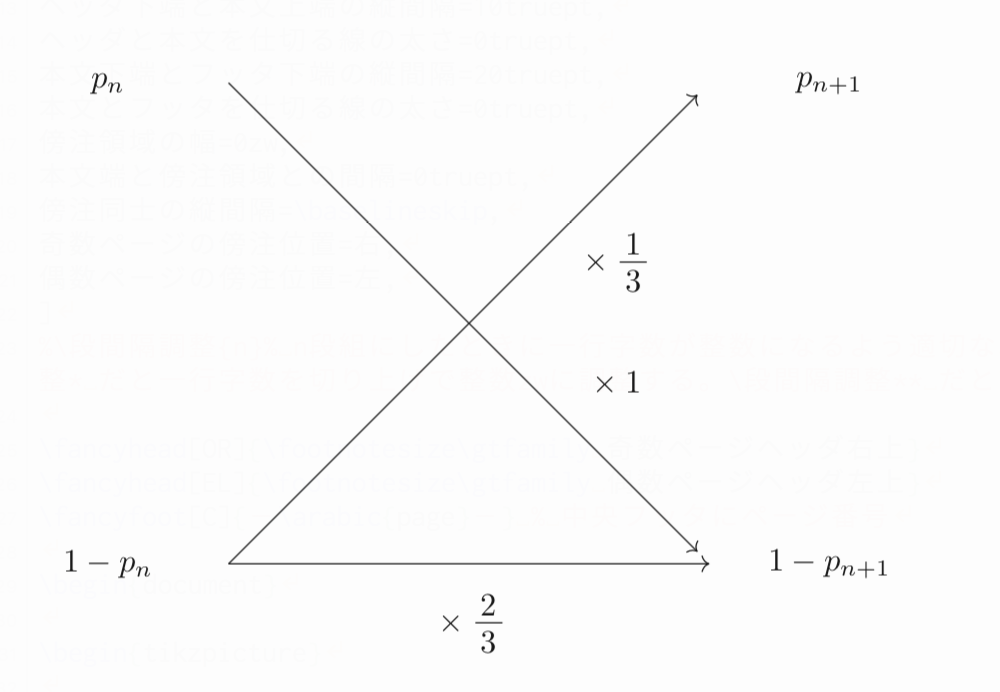
これを元に漸化式を立てることができますね!
\[p_{n+1}=\frac{1}{3}(1-p_n)\]
という漸化式が立つので、これを解いてあげればOKです。
ちなみに当たり前すぎることですが、
\[1-p_{n+1}=p_n+\frac{2}{3}(1-p_n)\]
の方を選んで漸化式を立てたとしても変形すれば全く同じ式になります。どっちで漸化式を立てればいいんだろうとか悩まないでくださいね。
初項は、$p_0=1$を選べばよいでしょう。
問題1の模範解答
私が実際に答案を作るなら、以下のようになります。
はじめに平面に接していた面をAと名付ける。
$n$回の操作のあとにAが平面に接する確率を$p_n$とおけば、遷移図は以下のようになる。

遷移図より、
\[p_{n+1}=\frac{1}{3}(1-p_n)\Leftrightarrow p_{n+1}-\frac{1}{4}=-\frac{1}{3}\left(p_n-\frac{1}{4}\right)\]
$p_0=1$であるので、
\[\boldsymbol{p_n=\frac{1}{4}\left\{1-\left(-\frac{1}{3}\right)^{n-1}\right\}}\]
先ほど述べた、$n\rightarrow\infty$のときの確率について考えてみると、
\[\lim_{n\to\infty}\frac{1}{4}\left\{1-\left(-\frac{1}{3}\right)^n\right\}=\frac{1}{4}\]
となるので、正しそうですね。
問題2(正三角形の10個の部屋と確率漸化式)の解答・解説
問題1はかなり簡単な確率漸化式の問題ですが、問題2はこの記事で述べた解き方、ポイント、コツを集約したような素晴らしい良問です。これをマスターしていれば、確率漸化式の大事な部分はほぼ理解したと言ってよいでしょう。
問題2を解く上でのポイント
まずは、文字設定を行っていきましょう。
部屋が10個あるからといって、10文字も置くようなことはしてはいけませんよね。正三角形は左右対称になっており、その中心にPの部屋があるので、中心軸に関して対称な部屋はまとめて扱うことができます。
よって、下図のようにA〜EとPの6種類の部屋に分けて考えれば良さそうです。
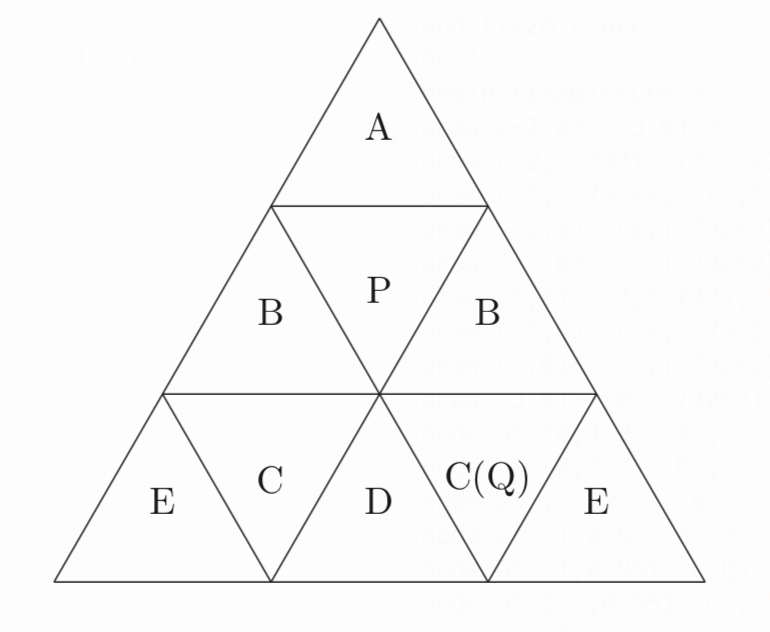
さて、これらそれぞれの部屋にいる確率を文字で置いてしまうと、すべての確率を足したときに1になるということを考慮しても5文字設定する必要が出てきてしまい、「3種類以上の数列の連立漸化式を解くことはほとんどない」という上で述べたポイントに反してしまいます。
そこで、偶奇性に着目すれば、もっと文字数を減らせるのではないかと考えます。
6種類の部屋を「PとC」、「AとBとDとE」の2グループに分けて見てみると始めは球は前者のグループにあり、1秒後には後者のグループ、2秒後は前者のグループ…
というように、球はこの2つのグループを1秒毎に交互に行き来していることが容易にわかります。
よって、Qの部屋にいる確率は、奇数秒後には$0$となっているので、偶数秒後のときしか考えなくて良いと分かります。
偶数秒後について考えるだけであれば、PとCの2つの部屋だけなので、確率の和が$1$になることも考慮すると、置くべき文字は1つだけで済みますね。
このように偶数秒後と奇数秒後で球が存在する部屋が限られているという事実は数学的帰納法によって証明すればよいでしょう。
あとは、遷移図を描いて、漸化式を立てて、それを解いてあげれば確率が求まります。
問題2の模範解答
私が実際に答案を作るなら、以下のようになります。
まず、対称性より、以下のように部屋に名前をつけると、同じ名前の部屋であれば、$n$秒後にその部屋に球がある確率は等しい。

ここで、「偶数秒後はP、Cの部屋にのみ球が存在し、奇数秒後にはA、B、D、Eのみ球が存在すること」を数学的帰納法によって示す。
(i)$n=0$のとき、
たしかに球はPに存在する。
(ii)$n=2k$($k$は$0$以上の整数)のとき、
球が部屋P、Cのどれかにあったと仮定すると、図より、$n=2k+1$秒後には球はA、B、D、Eのどれかにある。
(iii)$n=2k+1$($k$は$0$以上の整数)のとき、
球が部屋A、B、D、Eのどれかにあったと仮定すると、図より、$n=2k+2$秒後には球はP、Cのどれかにある。
以上より、「偶数秒後はP、Cの部屋にのみ球が存在し、奇数秒後にはA、B、D、Eのみ球が存在すること」が示された。
よって、$n$が偶数の時のみ考えればよい。$n$秒後にCのどちらかの部屋に球がある確率を$c_n$とおくと、$n$が偶数のとき、球はP、Cのどちらかにのみ存在し、Cの2つの部屋にある確率は等しいので、Pの部屋にある確率は$1-c_n$求める確率は$\frac{c_n}{2}$となる。
$n$秒後にPの部屋に球があるとき、2秒後は$\frac{1}{3}$の確率でCの部屋に遷移し、$n$秒後にCの部屋に球があるとき、2秒後は$\frac{1}{6}$の確率でPの部屋に遷移するので、遷移図は以下のようになる。
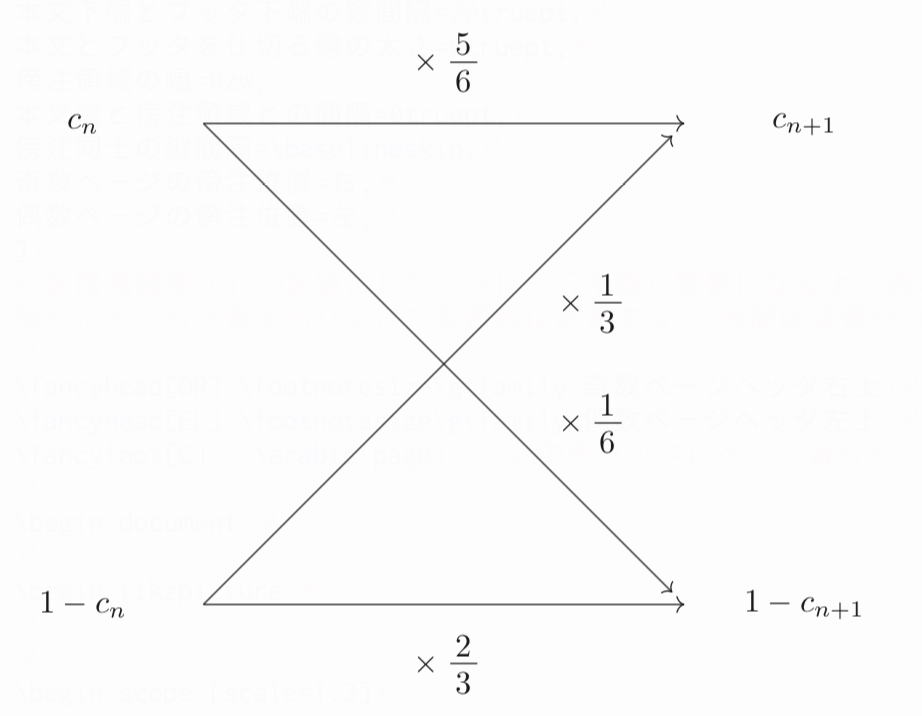
遷移図より、
\[\begin{align*}&c_{n+2}=\frac{5}{6}c_n+\frac{1}{3}(1-c_n)\\\Leftrightarrow &c_{n+2}-\frac{2}{3}=\frac{1}{2}\left(c_n-\frac{2}{3}\right)\end{align*}\]
$c_0=0$であるので、$n$が偶数のとき、
\[c_n=\frac{2}{3}\left\{1-\left(\frac{1}{2}\right)^{\frac{n}{2}}\right\}\]
であるので、求める確率は、
\[\left\{\begin{array}{l}\boldsymbol{0(nが奇数のとき)}\\\boldsymbol{\frac{1}{3}\left\{1-\left(\frac{1}{2}\right)^{\frac{n}{2}}\right\}(nが偶数のとき)}\end{array}\right.\]
$n\rightarrow\infty$のときの確率について考えてみると、
\[\lim_{n\to\infty}\frac{1}{3}\left\{1-\left(\frac{1}{2}\right)^{\frac{n}{2}}\right\}=\frac{1}{3}\]
となり、PとCの計3つの部屋が対称な位置にあることも考慮すると、正しそうですね。
まとめ
確率漸化式は、確率と数列が融合した分野であり、文字を置いて遷移図を描き、漸化式を立てて解くだけですが、対称性や偶奇性に注目するなどのポイント・コツがあることがわかったと思います。
入試でも頻出の確率漸化式ですが、一度慣れてしまえば、どんな確率漸化式の問題にも対応できるようになるので、「お得な分野」だと言えます。ぜひ、たくさん演習問題を解いて慣れていってください。







