この記事を読むと分かること
・漸化式とは何か
・漸化式の全10パターンが何なのか
・漸化式のそれぞれのパターンの関係性
・各パターンの重要度
そもそも漸化式とは?
漸化式(ぜんかしき)とは、数列の各項の関係式を定めることによって、数列全体を定義するための式のことです。たとえば、数列の隣り合った項は等しいという漸化式は、$n$番目の項と$n+1$番目の項が等しいというのを数式化すればよいので、$a_{n+1}=a_n$というように表します。
漸化式の解き方のコツは?
結論から言って、漸化式を解くコツというのは存在せず、それぞれのパターンの解き方を覚えるしか方法がありません。
しかしながら、漸化式の解き方を覚えるコツならあります。
学校で漸化式を習った時に躓いてしまった人の多くは、
1.同じパターンに対して解き方が複数あってどれを使えばいいかわからない
2.パターンが多すぎて解き方を覚えきれない
このどちらかに当てはまるのではないでしょうか?
実は漸化式は、1つのパターンに1つの最も優れた解法だけを覚えて、しかも、それぞれのパターンを覚える順番を工夫するだけで圧倒的に効率的に覚えられるようになります。
漸化式のパターン一覧
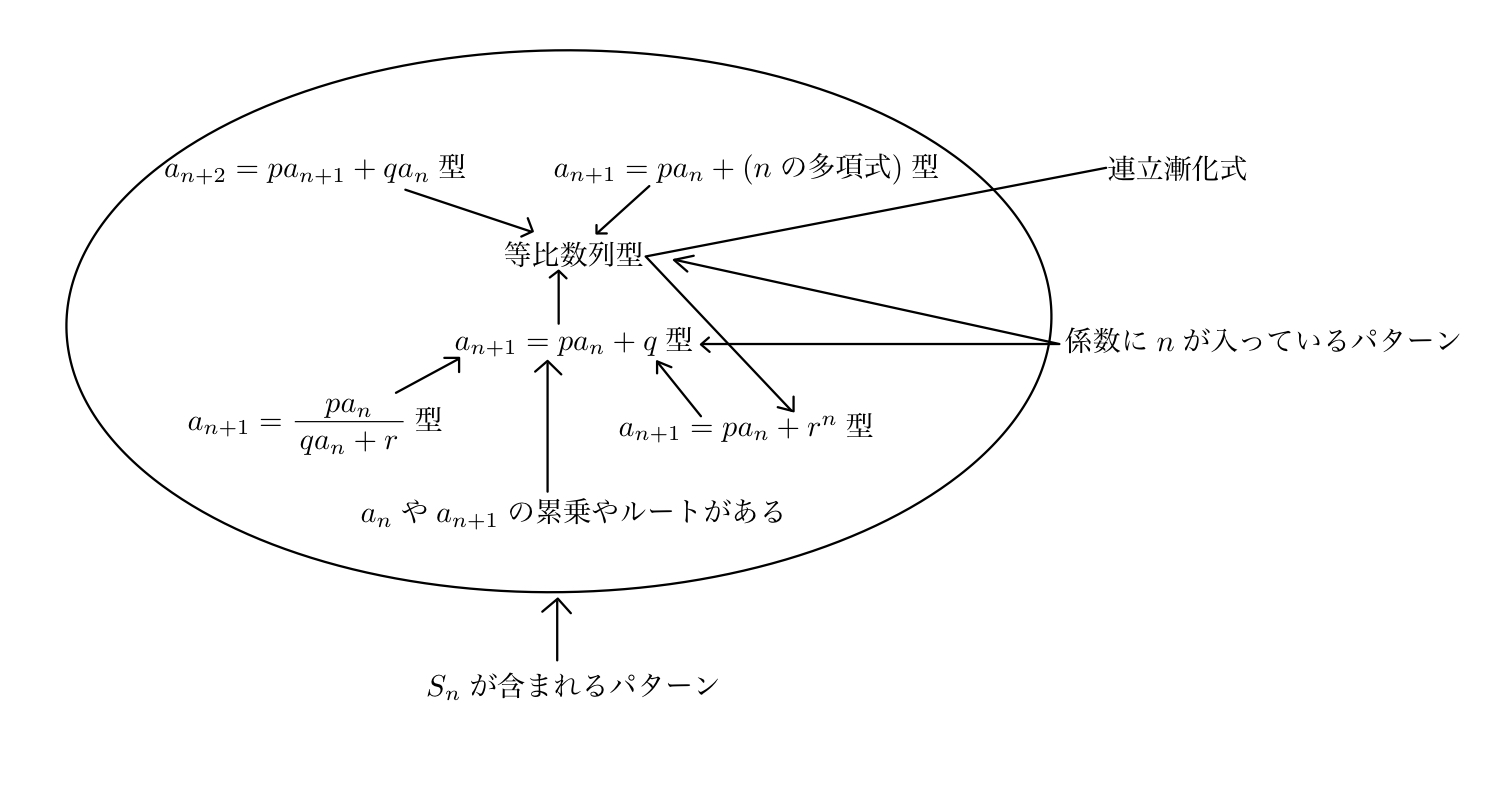
漸化式は全部で10パターンあり、一番最後に説明する、数学的帰納法を用いるパターン以外は上のフローチャートのような関係になっています。
基本的には等比数列型に帰着させるのが最終的な目的になっていることが分かると思います。
この記事では、大学受験で問われる漸化式のすべてのパターンを網羅し、さらに、上図のフローチャートが理解しやすいように関連性の高い順番に並べ替えて書いていきます。また、タイトルのところには大学受験での出題頻度を考慮して重要度を3段階で評価しています。
これを読めばあなたも漸化式マスターになれるはずです!
$a_{n+1}=pa_n+q$型の漸化式の解き方
最も一般的な漸化式の形である$a_{n+1}=pa_n+q$型の漸化式の解き方を学びましょう。他のタイプの漸化式を変形するとこの漸化式に帰着される頻度が非常に高いので、重要度は★★★です。
例題として、以下の問題を考えましょう。
例題
\[a_1=3,\,a_{n+1}=2a_n-1\]
なる数列$\{a_n\}$の一般項を求めよ。
$a_n=a_{n+1}=\alpha$とした特性方程式を解く
まず、$a_{n+1}=pa_n+q$の漸化式を解く時には、$a_{n+1}$と$a_n$を$\alpha$に置き換えてできる方程式を解くことになります。この方程式を特性方程式と呼びます。
上の例題において、特性方程式を考えると、
\[\alpha=2\alpha-1\Leftrightarrow \alpha=1\]
と求めることができました。
$a_{n+1}-\alpha=p(a_n-\alpha)$として等比数列型に帰着
元の方程式から特性方程式を辺々引いてあげれば、
\[a_{n+1}-\alpha=p(a_n-\alpha)\]
となり、数列$\{a_n-\alpha\}$を新しい数列と見ると、公比が$p$の等比数列になっていることがわかります。よって、$\boldsymbol{\alpha}$を求めたあとは$\boldsymbol{a_{n+1}-\alpha=p(a_n-\alpha)}$の形に変形してあげて、あとは計算するだけですね。
上の例題で考えると、先程$\alpha=1$と求まったので、
\[a_{n+1}-1=2(a_n-1)\]
と変形でき、$a_1=3$であることから、
\[a_n-1=2^{n-1}(3-1)\Leftrightarrow \boldsymbol{a_n=2^n+1}\]
となります。
$p=1$の場合はただの等差数列型!
$p=1$のときはただの等差数列型になることに気をつけましょう。
等差数列は、初項を$a$、公差を$d$とすれば、一般項は、
\[a_n=a+(n-1)d\]
と表されるので、上の例で言えば、
\[a_n=3+2(n-1)=2n+1\]
と求まります。
分数型の漸化式の解き方
さて、ここからは、変形を施すと$a_{n+1}=pa_n+q$型に帰着される場合について学んでいきます。
分数型の漸化式は比較的よく出てくる漸化式なので、重要度は★★です。
例題として、以下の問題を考えましょう。
例題
\[a_1=3,\,a_{n+1}=\frac{2a_n}{3a_n+1}\]
なる数列$\{a_n\}$の一般項を求めよ。
帰納的に$a_n\ne 0$を示す
分数型の漸化式では次項で説明するように、逆数を取るという操作を行います。このときに注意したいのが、
逆数を取る時には、0でないことを必ず確認せよ
ということです。
漸化式において逆数を取るという操作ができるのは、$\boldsymbol{a_n}$が常に0でないときのみですから、これを上手く示す必要が出てきます。
$a_n\ne 0$を示す時の記述はほとんど決まりきっており、2パターンの記述のしかたが考えられます。
漸化式において$a_n\ne 0$を示す方法2通り!
1.数学的帰納法
2.背理法
記述が簡単なのは1の方ですね。
実際に上の例題で記述をしてみましょう。
題意の漸化式において、$a_1=3>0$であり、また、$a_n>0$であれば、$a_{n+1}=\frac{2a_n}{3a_n+1}$より$a_{n+1}>0$であるから、帰納的に$a_n>0$が言える。
こんな感じのあっさりした記述で十分です。
数学的帰納法は本来もっと長いんですが、あくまで数列を解くことがメインであり、この記述はおまけであるので、このくらいあっさりした記述で全く問題ありません。
数学的帰納法がわからない方はこちらの記事を読んでください。
ちなみに、2の背理法を用いる方で記述すると、このようになります。
ある自然数$n$で$a_n=0$となると仮定すると、$a_{n+1}=\frac{2a_n}{3a_n+1}$より、$a_{n-1}=0$も言えて、これを繰り返すと$a_1=0$が言えるが、これは$a_1=3$と矛盾する。したがって、元の仮定が誤りであり、$a_n\ne 0$が言える。
漸化式の逆数を取って$a_{n+1}=pa_n+q$型に帰着
$a_n\ne 0$を示せたらあとは逆数を取ると、先ほど説明した$a_{n+1}=pa_n+q$型の漸化式に帰着することができます。例題を解きながら説明していきます。
題意の漸化式は両辺とも常に0でないので、両辺の逆数を取ることができて、
\[\frac{1}{a_{n+1}}=\frac{3a_n+1}{2a_n}\Leftrightarrow \frac{1}{a_{n+1}}=\frac{1}{2}\cdot\frac{1}{a_n}+\frac{3}{2}\]
と変形できます。ここで$\boldsymbol{\left\{\frac{1}{a_n}\right\}}$を新しい数列として考えれば、$\boldsymbol{a_{n+1}=pa_n+q}$の形になっていることがわかりますね。
あとは、同じように解いていくだけです。特性方程式の解は$\alpha=3$なので、
\[\frac{1}{a_{n+1}}=\frac{1}{2}\cdot\frac{1}{a_n}+\frac{3}{2}\Leftrightarrow \frac{1}{a_{n+1}}-3=\frac{1}{2}\left(\frac{1}{a_n}-3\right)\]
と同値変形することができて、$a_1=3$であることから、
\[\begin{align*}&\frac{1}{a_n}=\left(\frac{1}{2}\right)^{n-1}\left(\frac{1}{3}-3\right)+3\\\Leftrightarrow &\boldsymbol{a_n=\frac{3\cdot2^{n-4}}{-1+9\cdot2^{n-4}}}\end{align*}\]
と求めることができました。
逆数を取るために$a_n\ne 0$を示さなければならないという点ができるようになれば簡単に解けますね。
累乗やルートがある漸化式の解き方
次は、ルートや累乗の形が含まれる漸化式について考えていきます。これは先ほどの分数型の漸化式と解法はかなり似ていますが、こちらの漸化式は問題の中で自然に出てくることは少なく、重要度は★です。
例題として、以下の問題を考えましょう。
例題
\[a_1=2,\,a_{n+1}=3{a_n}^2\]
なる数列$\{a_n\}$の一般項を求めよ。
漸化式の両辺が正であることを確認する
$a_n$や$a_{n+1}$のルートや累乗が含まれた漸化式では、両辺の対数を取るという操作を行います。対数を扱う時の注意点として、
対数を扱うときは、まず真数条件と底条件を考えよ
というのがありましたから、真数が正であること、すなわち漸化式において両辺が常に正であることを確かめる必要性があります。
実際に上の例題で記述をしてみましょう。
題意の漸化式において、$a_1=2>0$であり、また、$a_n>0$であれば、$a_{n+1}=3{a_n}^2$より$a_{n+1}>0$であるから、帰納的に$a_n>0$が言える。
漸化式の対数を取って$a_{n+1}=pa_n+q$型に帰着
漸化式の両辺が正であることを示せたら、両辺に対数を取ることができます。
底を3とする対数を取ると、
\[\log_3{a_{n+1}}=1+2\log_3{a_n}\]
となります。ここで、$\boldsymbol{\left\{\log{a_n}\right\}}$を新しい数列として考えれば、$\boldsymbol{a_{n+1}=pa_n+q}$の形になっていることがわかりますね。
あとは、同じように解いていくだけです。特性方程式の解は$\alpha=-1$なので、
\[\log_3{a_{n+1}}+1=2\left(\log_3{a_n}+1\right)\]
と同値変形することができて、$a_1=2$であることから、
\[\begin{align*}&\log_3{a_n}=2^{n-1}\left(\log_3{2}+1\right)-1\\\Leftrightarrow &\boldsymbol{a_n=3^{2^{n-1}\left(\log_3{2}+1\right)-1}}\end{align*}\]
となります。
対数型の漸化式では分数型の漸化式を解くときと同じような記述をすることになるのがわかったと思います。
指数関数型の漸化式の解き方
次は、$a_{n+1}=pa_n+r^n$型(指数関数型)の漸化式の解き方です。このタイプの漸化式は、確率と漸化式を絡めた確率漸化式の問題でよく出てくるタイプの漸化式であり、重要度は★★★です。
例題として、以下の問題を考えましょう。
例題
\[a_1=3,\,a_{n+1}=2a_n-3^n\]
なる数列$\{a_n\}$の一般項を求めよ。
$r^{n+1}$で両辺を割って$a_{n+1}=pa_n+q$型に帰着させる
指数関数型の漸化式の解き方は$\boldsymbol{r^{n+1}}$で両辺を割るという操作を行うだけです。$r^n$の部分の指数が$n+1$や$n-1$になっていたとしても全く同じ操作でOKです。
実際に上の例題でやってみましょう。
$a_{n+1}=2a_n-3^n$の両辺を$3^{n+1}$ で割ると、
\[\frac{a_{n+1}}{3^{n+1}}=\frac{2}{3}\cdot\frac{a_n}{3^n}-\frac{1}{3}\]
となります。ここで、$\left\{\frac{a_n}{3^n}\right\}$を新たな数列として見ればたしかに$a_{n+1}=pa_n+q$型になっていることがわかると思います。
あとは、同じように解くだけです。
特性方程式の解は$\alpha=-1$ですから、
\[\frac{a_{n+1}}{3^{n+1}}=\frac{2}{3}\cdot\frac{a_n}{3^n}-\frac{1}{3}\Leftrightarrow\frac{a_{n+1}}{3^{n+1}}+1=\frac{2}{3}\left(\frac{a_n}{3^n}+1\right)\]
と同値変形することができて、$a_1=3$より、
\[\frac{a_n}{3^n}=\left(\frac{2}{3}\right)^{n-1}(1+1)-1\Leftrightarrow \boldsymbol{a_n=3\cdot 2^n-3^n}\]
と答えが求まりました。
$p=r$のときは等差数列型に帰着されることに注意
$a_{n+1}=pa_n+q$型の漸化式の解き方の説明のときにも注意点として説明しましたが、等差数列型の場合には「特性方程式を解いて〜」という流れではなくなることに注意しましょう。
例題を少し変えて、
\[a_1=3,\,a_{n+1}=3a_n-3^n\]
なる数列$\{a_n\}$の一般項を求めよ。
という問題を考えてみましょう。
$3^{n+1}(>0)$で割ったあとは等差数列型に帰着されるので、
\[\begin{align*}a_{n+1}=3a_n-3^n\Leftrightarrow &\frac{a_{n+1}}{3^{n+1}}=\frac{a_n}{3^n}-\frac{1}{3}\\\Leftrightarrow &\frac{a_{n+1}}{3^{n+1}}-\frac{a_n}{3^n}=-\frac{1}{3}\end{align*}\]
と変形を進めることになります。
$\left\{\frac{a_n}{3^n}\right\}$を新たな数列として見れば等差数列型になっているので、
\[\frac{a_n}{3^n}=1-\frac{1}{3}(n-1)\Leftrightarrow \boldsymbol{a_n=(-n+4)3^{n-1}}\]
と求まります。
三項間漸化式の解き方
今までは$a_{n+1}$と$a_n$のといった隣り合った二項の関係を示した隣接二項間漸化式について説明しましたが、$a_{n+1}$と$a_n$から$a_{n+2}$が決まるものは隣接三項間漸化式と呼ばれます。
これは、場合の数や確率に漸化式が絡むような問題でよく出てくるので、重要度は★★★です。
例題として、以下の問題を考えましょう。
例題
\[a_1=2,\,a_2=3,\,a_{n+2}=2a_{n+1}+3a_n\]
なる数列$\{a_n\}$の一般項を求めよ。
$a_{n+2}$を$t^2$、$a_{n+1}$を$t$、$a_n$を$1$とした特性方程式を解く
$a_{n+1}=pa_n+q$型の解法と同様に、特性方程式を解いて等比数列型への帰着を目指すのが三項間漸化式の最も大事な部分です。
ただし、$a_{n+1}=pa_n+q$型のときとは特性方程式の形が異なることに注意しましょう。
三項間漸化式では、
\[\boldsymbol{a_{n+2}\rightarrow t^2,\,a_{n+1}\rightarrow t,\,a_n\rightarrow 1}\]
とした特性方程式を解く
例題で実際に特性方程式を解いてみましょう。
題意の漸化式において、$a_{n+2}\rightarrow t^2、a_{n+1}\rightarrow t、a_n\rightarrow 1$とすれば、
\[t^2=2t+3\Leftrightarrow (t+1)(t-3)=0\Leftrightarrow t=-1,\,3\]
というように、特性方程式(2次方程式)が出てきて、その解を求めることができました。
$a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$と変形して等比数列型に帰着
先ほど求めた2解に$\alpha,\,\beta$と名前を付けましょう。これはどちらが$\alpha$でどちらが$\beta$でも構いません。特性方程式の解が重解だった場合には$\alpha=\beta$になります。
すると、実は与えられた漸化式は、
\[\begin{align*}&\boldsymbol{a_{n+2}=pa_{n+1}+qa_n}\\\boldsymbol{\Leftrightarrow} &\boldsymbol{a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)}\end{align*}\]
と同値変形することができるんです。
$\{a_{n+1}-\alpha a_n\}$を新しい数列として見れば、等比数列型になっていることがわかると思います。
どうして先ほどの特性方程式の解を用いるとこのような変形ができるのでしょうか?
\[\begin{align*}&a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)\\\Leftrightarrow &a_{n+2}=(\alpha+\beta)a_{n+1}-\alpha\beta a_n\end{align*}\]
という変形を見ればもう分かるでしょう。つまり、上の式を満たすような$\alpha,\,\beta$は、
\[\alpha+\beta=p,\,\alpha\beta=-q\]
を満たすような数であり、解と係数の関係の逆から、$\alpha,\,\beta$は$t$の2次方程式$t^2-pt-q=0$の2解だと言えますね。
これは、漸化式において$a_{n+2}\rightarrow t^2、a_{n+1}\rightarrow t、a_n\rightarrow 1$としたものと等しいので、先ほどの特性方程式の解を用いて等比数列型に変形ができるわけです。
例題においては、特性方程式を解いて求まった解を用いて、$-1$を$\alpha$に、$3$を$\beta$に対応させて考えれば、
\[\begin{align*}&a_{n+2}=2a_{n+1}+3a_n\\\Leftrightarrow &a_{n+2}+a_{n+1}=3(a_{n+1}+a_n)\end{align*}\]
と変形することができて、$a_1=2,\,a_2=3$であるから、
\[a_{n+1}+a_n=3^{n-1}(2+3)\Leftrightarrow a_{n+1}+a_n=5\cdot 3^{n-1}\]
指数関数型の漸化式を解く
$\{a_{n+1}-\alpha a_n\}$の一般項が求まりましたが、これには$\beta ^{n}$の形が含まれているので、$\beta=1$の時以外はすべて、$a_{n+1}=pa_n+r^n$型の漸化式が出てくることになります。
この解き方は前述の通りです。例題を解いてみましょう。
\[a_{n+1}+a_n=5\cdot 3^{n-1}\]
の両辺を$3^{n+1}(>0)$で割って、
\[\frac{a_{n+1}}{3^{n+1}}+\frac{1}{3}\cdot\frac{a_n}{3^n}=\frac{5}{9}\]
と変形すると、$a_{n+1}=pa_n+q$型になります。特性方程式の解は$\frac{5}{12}$なので、
\[\begin{align*}&\frac{a_{n+1}}{3^{n+1}}+\frac{1}{3}\cdot\frac{a_n}{3^n}=\frac{5}{9}\\\Leftrightarrow &\frac{a_{n+1}}{3^{n+1}}-\frac{5}{12}=-\frac{1}{3}\left(\frac{a_n}{3^n}-\frac{5}{12}\right)\end{align*}\]
と変形できます。$a_1=2$より、
\[\begin{align*}&\frac{a_n}{3^n}=\left(-\frac{1}{3}\right)^{n-1}\left(\frac{2}{3}-\frac{5}{12}\right)+\frac{5}{12}\\\Leftrightarrow &\boldsymbol{a_n=\frac{3}{4}\cdot(-1)^{n-1}+\frac{5}{4}\cdot3^{n-1}}\end{align*}\]
と求めることができました。
重解でなければ$\alpha,\,\beta$を入れ替えた2式を立ててもよい
さて、先ほどの解法よりももう少しはやく解く裏技があります。原則として、上の解法で解くべき(というより、上の解法で覚えていると暗記事項が少ない)ですが、特性方程式の解が重解でない場合に限っては以下の解法も有効です。
特性方程式の解はどちらを$\alpha,\,\beta$と見てもよかったわけなので、
\[\begin{align*}&a_{n+2}=pa_{n+1}+qa_n\\\Leftrightarrow &\left\{\begin{array}{l}a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)\\a_{n+2}-\beta a_{n+1}=\alpha(a_{n+1}-\beta a_n)\end{array}\right.\end{align*}\]
の2通りに変形できることがわかります。
したがって、それぞれにおいて、$a_{n+1}-\alpha a_n$と$a_{n+1}-\beta a_n$を求めて、$a_{n+1}$を消去すれば$a_n$を求めることができます。
先ほどの例題をこの解法で解いてみましょう。
\[\begin{align*}&a_{n+2}=2a_{n+1}+3a_n\\\Leftrightarrow &\left\{\begin{array}{l}a_{n+2}+a_{n+1}=3(a_{n+1}+a_n)\\a_{n+2}-a_{n+1}=-(a_{n+1}-3a_n)\end{array}\right.\end{align*}\]
の2通りに変形できるので、それぞれにおいて、$a_1=2,\,a_2=3$から、
\[\left\{\begin{array}{l}a_{n+1}+a_n=5\cdot3^{n-1}\\a_{n+1}-3a_n=-3\cdot(-1)^{n-1}\end{array}\right.\]
と求まるので、辺々引いて$a_{n+1}$を消去して、
\[\begin{align*}&4a_n=5\cdot3^{n-1}+3\cdot(-1)^{n-1}\\\Leftrightarrow &\boldsymbol{a_n=\frac{5}{4}\cdot3^{n-1}+\frac{3}{4}\cdot(-1)^{n-1}}\end{align*}\]
と求まります。
この解法の良いところとして、はやく解けて、計算ミスが起こりにくいことが挙げられますが、この解法だけを覚えていると特性方程式が重解を持つ場合には対応できません。
そこで、覚える事項を最小限にするには、まずは重解の場合にも対応できるはじめに挙げた解法を覚えましょう。余力があればこちらの解法も覚えてください。
$a_{n+1}=pa_n+(nの多項式)$型の解き方
ここからは、上で述べた漸化式の解き方との関連性は低く、個別に覚えなければならない漸化式の解き方を学びます。
まずは、$a_{n+1}=pa_n+q$型の$q$の部分が$n$の多項式になっているパターンについて見ていきます。これは頻出のものではありませんが、和の中抜けという画期的な手法と似た作業をするという点で重要であり、重要度は★★です。
例題として、以下の問題を考えましょう。
例題
\[a_1,\,a_{n+1}=2a_n+3n^2+2n+1\]
なる数列$\{a_n\}$の一般項を求めよ。
多項式を文字でおく
まず、多項式が何次式なのかを確認します。それと同じ次数の多項式を適当な文字を使っておいてください。
例題では2次式になっているので、
\[g(n)=an^2+bn+c\]
を定めてあげればよいです。
$a_{n+1}-g(n+1)=p(a_n-g(n))$を満たす$g(n)$を探して等比数列型に帰着
漸化式を解くための基本は等比数列型に帰着させることでしたが、今回も等比数列型に帰着できるように、
$a_{n+1}-g(n+1)=p(a_n-g(n))$
が満たされるような係数を決定していきます。
例題で実際にやってみましょう。
となるので、
\[-an^2+(2a-b)n+a+b-c=3n^2+2n+1\]
が$n$についての恒等式になるような$a,\,b,\,c$を定めればOKですね。
\[\left\{\begin{array}{l}-a=3\\2a-b=2\\a+b-c=1\end{array}\right.\Leftrightarrow \left\{\begin{array}{l}a=-3\\b=-8\\c=-12\end{array}\right.\]
と求まるので、
と変形できることがわかります。$\{a_n+3n^2+8n+12\}$を新しい数列として見れば、等比数列型になっているので、$a_1=1$から、
\[\begin{align*}&a_n+3n^2+8n+12=24\cdot 2^{n-1}\\\Leftrightarrow &\boldsymbol{a_n=3\cdot 2^{n+2}-3n^2-8n-12}\end{align*}\]
と求まります。
多項式の次数が高くなるほど計算は面倒になりますが、計算内容としては連立方程式を解くだけなので計算ミスさえなければ必ず解けるはずです。
$p=1$の場合は階差数列の公式を用いて求める
$p=1$の場合には、上のような解法で解くことができません。階差数列がわかっているときには、$b_n=a_{n+1}-a_n$とすれば、
\[a_n=a_1+\sum_{k=1}^{n-1}b_k\]
として求めることができるんでしたね。この階差数列の公式を用いるときの注意点としては、
階差数列の公式を適用できるのは$\boldsymbol{n\geqq 2}$のときだけであることに注意せよ
というのがありました。
その点に気をつけて、あとは公式を使えばOKです。公式として、
\[\begin{align*}&\sum_{k=1}^{n}k=\frac{1}{2}n(n+1)\\&\sum_{k=1}^{n}k^2=\frac{1}{6}n(n+1)(2n+1)\\&\sum_{k=1}^{n}k^3=\left\{\frac{1}{2}n(n+1)\right\}^2\end{align*}\]
の3つを覚えていれば十分です。
係数にnが入っている漸化式の解き方
今まで扱ってきた漸化式はどれも、$a_n$や$a_{n+1}$の係数が定数になっていましたが、係数に$n$が含まれている場合にはどうすればよいのでしょうか。
入試問題でこのタイプの漸化式を解くことはほとんどないので、重要度は★です。
例題として、以下の問題を考えましょう。
例題
\[a_1=1,\,na_{n+1}=(n+1)a_n+n^3+3n^2+2n\]
なる数列$\{a_n\}$の一般項を求めよ。
上手く変形して定数係数の新たな数列の漸化式にする
このタイプの漸化式では、「この変形をすれば必ず解ける!」という定石があるわけではなく、上手い変形をすることによって係数が定数になっているような数列の漸化式と見れる形にしなければなりません。
例題の漸化式では、両辺を$(n+1)n(>0)$で割ると、
\[\begin{align*}&na_{n+1}=(n+1)a_n+n^3+3n^2+2n\\\Leftrightarrow &\frac{a_{n+1}}{n+1}=\frac{a_n}{n}+n+2\end{align*}\]
となるので、$\left\{\frac{a_n}{n}\right\}$を新たな数列と見れば、定数係数の漸化式に帰着できています。形としては、$a_{n+1}=pa_n+(nの多項式)$の形になっていますね。
また、$a_n$の係数が$1$になっているので先ほど説明した、階差数列の公式を用いて一般項を求めるパターンです。
$n\geqq 2$のとき、$a_1=1$なので、
\[\frac{a_n}{n}=1+\sum_{k=1}^{n-1}(k+2)=1+\frac{1}{2}(n-1)(n+4)\]
\[\therefore a_n = \boldsymbol{\frac{n(n^2+3n-2)}{2}}\]
と求まります。これは$n=1$のときも成立していますね。
基本的には、$a_n$や$a_{n+1}$の係数になっているものの積を両辺にかけたり割ったりすれば、上手く変形ができると思っておけばOKです。
$a_n$と$a_{n+1}$以外の項がなければ漸化式を繰り返し用いてもOK
上手い変形が思いつかなかった場合には漸化式を繰り返し用いると上手くいくケースもよくあります。これは、数学的に厳密かというと微妙なところなので、あくまで上手い変形を考えることを最優先するようにしてください。
例題では、$a_n$と$a_{n+1}$以外の項として$n^3+3n^2+2n$があったので、漸化式を繰り返し用いても上手く行きません。
与えられた漸化式が$na_{n+1}=(n+1)a_n$だった場合を考えてみましょう。
\[na_{n+1}=(n+1)a_n\Leftrightarrow a_{n+1}=\frac{n+1}{n}a_n\]
であり、$a_1=1$であるので、漸化式を繰り返し用いれば、
\[a_n=1\cdot \frac{2}{1}\cdot\frac{3}{2}\cdots\frac{n-1}{n-2}\cdot\frac{n}{n-1}=\boldsymbol{n}\]
と求めることができます。
このように、議論がやや曖昧であることと、$a_n$と$a_{n+1}$以外の項がない場合のみしか使えないなどの欠点はありますが、答えを簡単に求めることができるので、この解法も頭に入れておくとよいでしょう。
連立漸化式の解き方
さて、今までは$a_n$という1つの数列のみに関する話でしたが、複数の数列が絡み合うようにして定義されたものも存在します。
2つの数列によって互いを定義する連立漸化式は確率や場合の数の分野で頻出で、東京大学でも過去に何度も確率と連立漸化式を絡めた確率漸化式の問題が出題されています。重要度は★★★です。
例題として、以下の問題を考えましょう。
例題
\[a_1=1,\,b_1=1,\,\ \left\{\begin{array}{l}a_{n+1}=a_n+2b_n\\b_{n+1}=4a_n+3b_n\end{array}\right.\]
なる数列$\{a_n\},\,\{b_n\}$の一般項を求めよ。
1式目+2式目$\times\alpha$が等比数列型になるような$\alpha$を求める
連立漸化式においても、基本的な方針は変わらず、等比数列型に帰着させることを目指します。そこで、1式目+2式目$\times\alpha$という式を立てて、左辺と右辺において、$a_{n+1}$と$b_{n+1}$の係数の比が$a_n$と$b_n$の係数の比になるような$\alpha$を求めてあげれば等比数列型に帰着できます。
例題で実際にやってみましょう。1式目+2式目$\times\alpha$から、
\[a_{n+1}+\alpha b_{n+1}=(1+4\alpha)a_n+(2+3\alpha)b_n\]
となるので、等比数列型となるのは、
\[\begin{align*}&1:\alpha=(1+4\alpha):(2+3\alpha) \\\Leftrightarrow &4\alpha^2+\alpha=2+3\alpha\\\Leftrightarrow &(2\alpha+1)(\alpha-1)=0\\\Leftrightarrow &\alpha=1,\,-\frac{1}{2}\end{align*}\]
のときだと求まります。これを使って、等比数列型になるとき2パターンの式をそれぞれ立てて、解きましょう。
まず、$\alpha=1$のとき、1式目+2式目から、
\[a_{n+1}+b_{n+1}=5(a_n+b_n)\]
となるので、$\{a_n+b_n\}$を新しい数列と見れば等比数列型になっており、$a_1=1,\,b_1=4$より、
\[a_n+b_n=5^{n}\]
また、$\alpha=\frac{1}{2}$のとき、1式目+2式目$\times\left(-\frac{1}{2}\right)$から、
\[a_{n+1}-\frac{1}{2}b_{n+1}=-\left(a_{n+1}-\frac{1}{2}b_n\right)\]
となるので、$\left\{a_n-\frac{1}{2}b_n\right\}$を新しい数列と見れば等比数列型になっており、$a_1=1,\,b_1=4$より、
\[a_n-\frac{1}{2}b_n=(-1)^n\]
$a_n,\,b_n$の連立方程式を解く
$a_n,\,b_n$についての式が2つ求まったので、あとは連立方程式を解くだけで求まりますね。
例題の場合、
\[\left\{\begin{array}{l}a_n+b_n=5^{n}\\a_n-\frac{1}{2}b_n=(-1)^n\end{array}\right.\]
という2式が求まったので、辺々差を取れば、
\[\frac{3}{2}b_n=5^n-(-1)^n\Leftrightarrow \boldsymbol{b_n=\frac{2}{3}\{5^n-(-1)^n\}}\]
となり、また2式目に$2$をかけて辺々足すと、
\[3a_n=5^n+2\cdot(-1)^n\Leftrightarrow \boldsymbol{a_n=\frac{1}{3}\{5^n+2\cdot(-1)^n\}}\]
と求まります。
連立漸化式では、等比数列型になるときを計算して探すという操作ができればあとは非常に簡単ですね。
対称なら2式を足し引きするだけ
上で説明した方針で必ず解けますが$a_n$と$b_n$が対称の時には2式を足し引きすれば等比数列型に帰着できるという事実は覚えておくと得でしょう。
そもそも対称式の扱い方として、
対称な2式は足し引きすると変形が上手く行くことが多い
というコツがありました。それは漸化式においても同様というわけですね。
例えば、与えられた漸化式が
\[\left\{\begin{array}{l}a_{n+1}=a_n+2b_n\\b_{n+1}=2a_n+b_n\end{array}\right.\]
のように対称な形だった場合には、2式を辺々足すと、$a_{n+1}+b_{n+1}=3(a_n+b_n)$、2式を辺々引くと$a_{n+1}-b_{n+1}=-(a_n-b_n)$となり、確かに等比数列型になっていることがわかると思います。
どうしてこうなるのでしょうか?
対称な漸化式は
\[\left\{\begin{array}{l}a_{n+1}=sa_n+tb_n\\b_{n+1}=ta_n+sb_n\end{array}\right.\]
の形で書けるので、1式目+2式目$\times\alpha$は、
\[a_{n+1}+\alpha b_n=(s+\alpha t)a_n+(t+\alpha s)b_n\]
となります。等比数列型になるときは、
\[1:\alpha=s+\alpha t:t+\alpha s=t\alpha^2-t=0\]
となり、今は$t\ne 0$のときを考えているので、$s,\,t$によらず、$\alpha=\pm1$で等比数列型になることがわかります。
$S_n=a_1+\cdots +a_n$を含む漸化式の解き方
複数の漸化式が絡む場合として、$\{a_n\}$の第$n$項までの総和$\{S_n\}$が出てくるパターンもあります。
これは大学入試での出題頻度は低いので重要度は★ですが、学校で数列を習う際には見かけることがあると思うので、一応解説しておこうと思います。
例題として、以下の問題を考えましょう。
例題
\[S_n=a_1+a_2+\cdots+a_n\]
によって定義された数列$\{S_n\}$がある。以下の漸化式を満たすとき、正の項のみからなる数列$\{a_n\}$の一般項を求めよ。
\[a_1=1,\,S_n=\frac{1}{2}a_n^2+\frac{1}{2}a_n\]
$S_n-S_{n-1}=a_n$を使って$S_n$または$a_n$のみの漸化式を作る
このタイプの漸化式の問題におけるポイントはただ1つです。
2つの数列が同じ漸化式の中に混在していては処理のしようがありませんから、一方を消去してしまえばいいわけです。
消去するための式として用いることができるのは、$S_n=a_1+a_2+\cdots +a_n$という$S_n$の定義式だけですよね。しかし、このままでは使い勝手が悪いので、$S_n-S_{n-1}=a_n$という形を用いるわけです。
注意したいのは、$\boldsymbol{S_{n-1}}$が定義されるのは$\boldsymbol{n\geqq 2}$のときであることです。
また、ポイントとして、消去する際には1つだけ数字をずらした漸化式との差を取ると楽な場合が多いです。
さて、今までの説明を使って例題を解いてみましょう。
まず、今回求めたいのは$S_n$ではなく$a_n$なので、$S_n$を消去したいですね。
$n\geqq 2$において1つだけ数字をずらした漸化式、
\[S_{n-1}=\frac{1}{2}a_{n-1}^2+\frac{1}{2}a_{n-1}\]
を持ち出して2式の差を取りましょう。辺々差を取ると、
\[S_n-S_{n-1}=\frac{1}{2}(a_n^2-a_{n-1}^2+a_n-a_{n-1})\]
$S_n-S_{n-1}=a_n$を用いると、
\[\begin{align*}&a_n=\frac{1}{2}(a_n^2-a_{n-1}^2+a_n-a_{n-1})\\\Leftrightarrow &a_n^2-a_n-a_{n-1}^2-a_{n-1}=0\\\Leftrightarrow &(a_n-a_{n-1}-1)(a_n+a_{n-1})=0\\\Leftrightarrow &a_n=a_{n-1}+1,\,-a_{n-1}\end{align*}\]
求まった漸化式を解く
$a_n$だけが含まれた漸化式が求まれば、あとは解くだけです。例題においては2つの漸化式が出てきましたが、問題文には「正の項のみからなる」と書いてあるので、$a_n=-a_{n-1}$となることはありえないですね。
よって、$a_n=a_{n-1}+1$であって、これは等差数列型になっているので、$a_1=1$から、
\[a_n=n\]
と求めることができます。
見慣れていないと難しく感じてしまいますが、覚えておくべき事項も少なく、簡単に解けますね。
上のどのパターンにも当てはまらない漸化式の解き方
ここまでたくさん漸化式の解き方を説明してきましたが、これらすべての解き方を暗記していたとしても解けないパターンの漸化式があります。
大学受験において、知らないパターンの漸化式の解き方はただ1つです。この手法は、単に漸化式の解き方を忘れてしまった場合においても有効な手段となることがあるので、覚えておくべきでしょう。重要度は★★★です。
例題として、以下の問題を考えましょう。
例題
\[a_n>0,\,a_1=1,\,a_{n+1}=\sqrt{a_na_{n+1}+n+1}\]
なる数列$\{a_n\}$の一般項を求めよ。
はじめのいくつかの項を求めてみる
まず、よくわからない漸化式に遭遇したときにやるべきことは、$\boldsymbol{a_1,\,a_2,\,a_3}$などのはじめのいくつかの項がどのような値になるのか調べることです。
例題の漸化式を見てみると、$a_na_{n+1}$の項などがあり、今まで上で説明してきたどのパターンにも当てはまらないのがすぐに分かると思います。
そこで、例題で実際に$a_2$や$a_3$を求めてみましょう。
与えられた漸化式に$n=1,\,a_1=1$を代入して、
\[a_2=\sqrt{a_2+2}\]
題意より、$a_2>0$であるから、両辺2乗しても同値で、
\[{a_2}^2=a_2+2\Leftrightarrow a_2=-1,2\]
$a_2>0$なので、
\[a_2=2\]
と求まります。
同様にして、
\[a_3=3\]
も求まります。
一般項を予想して数学的帰納法!!
はじめの数項を実際に見てみると、一般項がどのようになるか想像がつく場合があります。今回の例題では、「$a_n=n$になるんじゃないか…?」となんとなく予想がつきそうですよね。
数学では単なる予想を示すだけでは意味がありません。そこで、この予想が正しいことを示しましょう!
証明に使うのは数学的帰納法という手法です。数学的帰納法については以下の記事で詳しく説明しているので、まだ数学的帰納法を理解していない人や、数学的帰納法を使った入試問題に興味のある方は読んでみてください。
例題において記述を作った場合の例を以下に示しておきます。
$a_n=n$であることを数学的帰納法によって示す。
(i)$n=1$のとき、
$a_1=1$よりたしかに$a_n=n$が成り立つ。
(ii)$n=k$($k$は自然数)のとき、$a_n=n$が成立すると仮定すると、題意の漸化式より、
\[a_{k+1}=\sqrt{ka_{k+1}+k+1}\]
題意より、$a_{k+1}>0$であるから、両辺2乗しても同値で、
\[a_{k+1}^2=ka_{k+1}+k+1\Leftrightarrow a_{k+1}=-1,\,k\]
$a_{k+1}>0$より、
\[a_{k+1}=k+1\]
よって、$k=n+1$のときも成り立つ。
したがって、題意成立。
以上のように、予想ができたあとは簡単に示せます。
今まで説明してきた漸化式はすべて、一般項がどうなるか予想できるのであればこの手法で解くことができます。漸化式の解き方を忘れてしまった場合には、最悪この手法で解けないか一度試してみるとよいでしょう。
まとめ
大学受験で問われる漸化式の解き方には上で説明した10パターンがありますが、それぞれの関連性に注目して覚えていけばそれほど多くの手法を覚えずに済むことがわかったと思います。
漸化式は確率や場合の数と絡んでよくでてくるので、漸化式が解けないせいで点数を落としてしまったということのないようにしっかり覚えましょう。






