「液体で大さじ1/2は深さ2/3」と多くの料理本で言われます。実は私は最近料理教室に通っていて、そこでも同じことを言われました。
これって2/3で本当に正しいのでしょうか…?
こういうときは数学の力を借りれば解決しそうですね!
積分の知識を使って、「『大さじ1/2は深さ2/3』は数学的に正しいのか?」を証明してみたいと思います!
この記事を読むとわかること
・積分による、「大さじ1/2は深さ2/3」が正しいのかどうかの検証結果
・三角関数を用いた、大さじ1/2となるときの厳密な深さ
大さじ1/2はどのくらいの深さまで入れるべきか計算してみる
積分の知識を使えば、大さじ1/2がどのくらいの深さまで入れた時なのかは簡単に計算することができそうです。
大さじのスプーンを完全な半球だと仮定する
まずは、大さじのスプーンを数学の世界に引きずり込まなければいけません。そこで、大さじのスプーンを完全な半球だと仮定し、
\[x^2+y^2+z^2=1,\,z\geqq 0\]
で表される以下のような図形だとします。(ちょうど、スプーンを上下ひっくり返したような形になっています。)
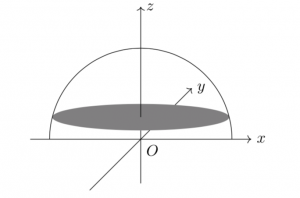
そして、$z=t(0<t<1)$という平面で切断したときに、ちょうどこの半球の体積が2等分されるような$t$を求めてあげればOKですね。さらに、$\boldsymbol{1-t}$がちょうど$\boldsymbol{\frac{2}{3}}$になったとすれば、料理の世界で言われていることは数学的にも正しいことになります。
半球の体積が2等分されるときの$\boldsymbol{t}$を積分によって求める
あとは、実際に積分計算を実行して、体積が2等分されるときの$t$を求めるだけです!半球の体積は、
\[\frac{1}{2}\cdot\frac{4}{3}\pi\cdot1^3=\frac{2}{3}\pi\]
なので、$z=t$によって分けられた下側の部分の体積がその半分の$\frac{1}{3}\pi$に一致するときを求めればOKです。
$z=t$によって切断したときの断面は半径が$\sqrt{1-t^2}$の円板になっているので、分けられた下側の部分の体積は、積分によって、
\[\int_{0}^{t}\pi(1-s^2)ds\]
と表されます。これを計算していくと、
\[\begin{align*}\int_{0}^{t}\pi(1-s^2)ds=&\pi\left[s-\frac{1}{3}s^3\right]^{t}_{0}\\=&\pi\left(t-\frac{1}{3}t^3\right)\end{align*}\]
となります。
これが、$\frac{1}{3}\pi$となるのは、
\[\pi\left(t-\frac{1}{3}t^3\right)=\frac{1}{3}\pi\Leftrightarrow t^3-3t+1=0\]
のときですね。
整数係数の方程式になっているので、有理数解の候補は、
\[\pm\frac{t^3の係数の約数}{定数項の約数}\]
となるため、$\pm1$しか有理数解の候補はありません。また、これらを代入してみても解でないことは容易にわかります。
よって、この3次方程式は有理数解を持たないので、厳密には深さ2/3まで入れても大さじ1/2にはならないことが示されました。
大さじ1/2は厳密にはどの深さまで入れればいい?
上の3次方程式の解は厳密にはどのような値になるのでしょうか?有理数解を持たないので、高校範囲の数学では上手く解けないのですが、結論を先に知っていれば以下のように解くことが可能です。
$f(t)=t^3-3t+1$とおくと、
\[f'(t)=3(t-1)(t+1)\]
であるので、増減表は以下のようになる。
\[\begin{array}{|C{2zw}||C{2zw}|C{2zw}|C{2zw}|C{2zw}|C{2zw}|} \hline
t&\cdots&-1&\cdots&1&\cdots\\
\hline f'(t)&+&0&-&0&+\\
\hline f(t)&\nearrow&3&\searrow&-1&\nearrow\\
\hline \end{array}\]
また、$f(-2)=-1<0$、$f(2)=3>0$であるので、$t^3-3t+1=0$の解はすべて実数解であり、しかも$-2< t< 2$の範囲にあることがわかる。
よって、$t^3-3t+1=0$の解は$t=2\cos{\theta}(0<\theta<\pi)$とおくことができて、これを元の方程式に代入すると、
\[\begin{align*}&(2\cos{\theta})^3-6\cos{\theta}+1=0\\\Leftrightarrow &2(4\cos^3{\theta}-3\cos{\theta})=-1\end{align*}\]
となる。
ここで、3倍角の公式より、
\[\cos{3\theta}=4\cos^3{\theta}-3\cos{\theta}\]
であるから、
\[2\cos{3\theta}=-1\Leftrightarrow\cos{3\theta}=-\frac{1}{2}\]
となる。$0<\theta<\pi$より、$0<3\theta<3\pi$であることも考慮すると、
\[3\theta=\frac{2}{3}\pi,\,\frac{4}{3}\pi,\,\frac{8}{3}\pi\Leftrightarrow\theta=\frac{2}{9}\pi,\,\frac{4}{9}\pi,\,\frac{8}{9}\pi\]
と求まる。
したがって、$t^3-3t+1=0$の3解は、
\[\boldsymbol{t=2\cos{\frac{2}{9}\pi},\,2\cos{\frac{4}{9}\pi},\,2\cos{\frac{8}{9}\pi}}\]
求めたかった値は0以上1未満の数なので、$2\cos{\frac{4}{9}\pi}$のみが該当します。
大さじの底から図った高さは1からこれを除いたものなので、
\[1-2\cos{\frac{4}{9}\pi}\]
が大さじ1/2にちょうどなる時の深さとなります。
結論
以上の議論から、数学的に厳密に考えた場合、大さじ1/2に対応する深さは2/3ではありません。正しくは、三角関数を用いることが許されるとすれば、
「深さ$\boldsymbol{1-2\cos{\frac{4}{9}\pi}}$のときが大さじ1/2」
ということになります。
しかしながら、関数電卓で、この値の近似値を算出すると、
\[0.65270\cdots\]
となるので、$\frac{2}{3}=0.66666\cdots$に非常に近い値になっていることがわかると思います。料理において、この程度の差は全く問題ないので、よって、
「料理をするときに大さじ1/2をはかりたいとき、目安にする深さは2/3で正しい」
という結論も得られました。
料理の本を読んで、この話題が出てきたら、ぜひ積分を思い出してくださいね。






