この記事を読むとわかること
・数学の軌跡の問題の解き方2通り
・それぞれの解き方における注意点
・軌跡に関する入試問題3つ
そもそも軌跡とは?
軌跡とは点が描く曲線または直線のこと
数学における『軌跡』とは、ある動く点が描く曲線または直線のことを指します。描く図形が面積が0でない図形となる場合は軌跡ではなく『領域』と呼ばれます。
数ⅠAⅡBの範囲では、この軌跡や領域を求めさせる分野を「軌跡と領域」とひとまとまりにして扱うことが多いです。
領域に比べて軌跡は簡単
領域を求める問題はまず手法自体の理解が難しく、また難問も多いのですが、それに比べて軌跡は解法や注意すべきポイントが決まりきっていて習得は簡単です。
この記事では軌跡の問題の解き方をはじめに解説していって、最後に軌跡を求める入試問題を3つ紹介したいと思います!
軌跡の問題の解き方は?
軌跡の問題の解き方は以下のたった2通りです!
軌跡の問題の解き方2通り
1.パラメータを消去する
2.図形的な考察をする
パラメータを消去する
軌跡の問題は、ある範囲を動く数(これを媒介変数やパラメータと呼びます)を用いて、
\[\left\{\begin{array}{l}x=(パラメータの式)\\y=(パラメータの式)\end{array}\right.\]
と表された点$(x,\,y)$がどのような図形上を動くのか調べる問題であることがほとんどです。
この2式からパラメータを消去すれば、$x,\,y$だけで表された式が出てきますよね。これはパラメータの値によらず常に成り立つ関係式であるので、すなわち、これが求めたい軌跡の方程式となります。
パラメータを消去して軌跡を求めるときに気をつけたいのは、パラメータの条件を$x,\,y$に反映させるということです。例えば、以下の問題を考えましょう。
$t$が$-1\leqq t\leqq 1$を動くとき、
\[\left\{\begin{array}{l}x=\frac{1}{2}t-1\\y=t^2-3t+1\end{array}\right.\]
を満たす点$\mathrm{P}(x,\,y)$が描く曲線を図示せよ。
このパラメータを消去するときには、
\[t=2x+2\]
と変形して$y=t^2-3t+1$に代入することになりますが、このときに必ず$-1\leqq t\leqq 1$にも代入して、$t$についていた条件を$x,\,y$に反映させないと正しい条件となりません。
以下の記事では、媒介変数表示された曲線を図示する方法を数Ⅲの範囲も含めて書いています。興味のある方は読んでみてください。
図形的考察をする
軌跡の問題は先ほどのように代数的に求めるべき軌跡が表されたものばかりではなく、図形的に定義された曲線の方程式を求めることがほとんどです。
このとき、その図形的関係を数式化して、上で説明したようにパラメータを消去するという方法で解くことはもちろんできます。しかし、代数の世界に持ち込まずに図形的考察をして軌跡を求めることができる場合も実はあります。
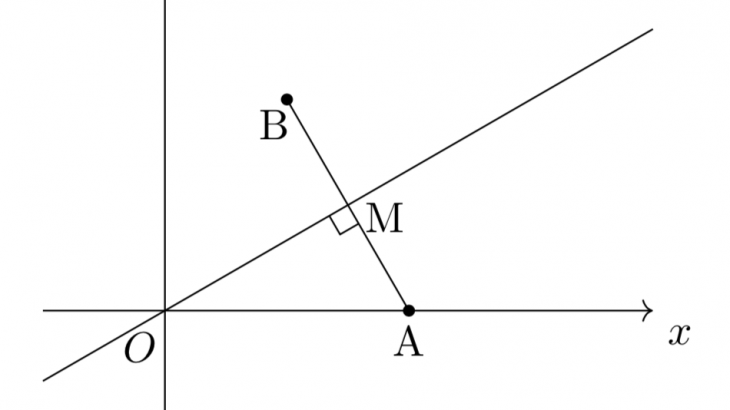
特に、直角が出てくるときに、動点が円を描くという場合が非常に多いです。例えば、$y=mx$($m$は任意の実数)という直線に$(2,\,0)$という点から下ろした垂線の足は以下の図のように変化します。

これを代数的に考えようとすると、原点から垂線の足に向かうベクトルは、ベクトル$(2,\,0)$の$(1,\,m)$の上への正射影ベクトルになるので、垂線の足の座標は、
\[\left(\frac{2}{1+m^2},\,\frac{2m}{1+m^2}\right)\]
となるので、ここから$m$を消去して…という流れになるはずです。これだと議論が長いですよね。
そこで、図形的な性質に着目しましょう。
円の直径に対する円周角は必ず$90^{\circ}$であり、逆に、ある2点から見て常に$90^{\circ}$をなす点の集合は、その2点を結ぶ線分が直径となる円になるということを考えると、求める軌跡は原点と$(2,\,0)$を結ぶ線分を直径とする円になることが分かります。
図形的考察によって軌跡を求めるときには計算要らずという利点がありますが、通らない範囲がないかには細心の注意を払わなければなりません。
上の例で言えば、原点と$(2,\,0)$を結ぶ線分を直径とする円が答えになると思って、
\[(x-1)^2+y^2=1\]
と書いてしまっては、不正解になってしまいます。
上の動画を見てみると、垂線の足は$m$の値がどんなに大きくなっても小さくなっても原点だけは通過しないことがわかります。
したがって、正しい答えは、
\[(x-1)^2+y^2=1(ただし(x,\,y)\ne(0,\,0))\]
となります。
パラメータ消去による解法の場合には、パラメータの条件を反映させるということを怠らなければ必ず正しい答えが出ますが、図形的考察は通過しない範囲についての考察を正確にしなければ正しい答えを得られません。
図形的考察を用いるときにはこの点に必ず注意しましょう。
軌跡に関する入試問題3つ
軌跡の求め方を学んだら、実際に軌跡に関する入試問題を解いていきましょう!
問題1
点$\mathrm{P}(x,\,y)$が$x^2+y^2=1$上を動くとき、点$\mathrm{Q}(x+2y+1,\,2x-y-1)$の軌跡を求めよ。
解答・解説
軌跡の問題では、1つのパラメータを消去する問題は非常に簡単に解くことができますが、今回の問題のように2文字のパラメータによって、動点が表されていることはよくあります。
今回の問題で言えば$x,\,y$の2文字がパラメータになっていますね。これらを消去するには、$x,\,y$について解いてあげてから、条件式に代入するだけでOKです。
以下、解答例です。
とおく。このとき、$x,\,y$について解くと、
\[\left\{\begin{array}{l}x=\frac{X+2Y+1}{5}\\y=\frac{2X-Y-3}{5}\end{array}\right.\]
となる。これを$x^2+y^2=1$に代入して、
\[\begin{align*}&\left(\frac{X+2Y+1}{5}\right)^2+\left(\frac{2X-Y-3}{5}\right)^2=1\\\Leftrightarrow & 5X^2+5Y^2-10X+10Y+10=25\\\Leftrightarrow & X^2+y^2-2X+2Y-3=0\\\Leftrightarrow & (X-1)^2+(Y+1)^2=5 \end{align*}\]
したがって求める軌跡は、
\[\boldsymbol{(x-1)^2+(y+1)^2=5}\]
単位円周上を点Pが動くときに点Qがどのように動くかを動画にすると以下のようになります。

問題2
$xy$平面上において、直線$y=mx$に関して点$\mathrm{A}$と対称な点を$\mathrm{B}$とする。$m$が任意の実数を動くとき、点$\mathrm{B}$の軌跡を求めよ。
解答・解説
まずは、図を描いてみると以下のような状況になっています。
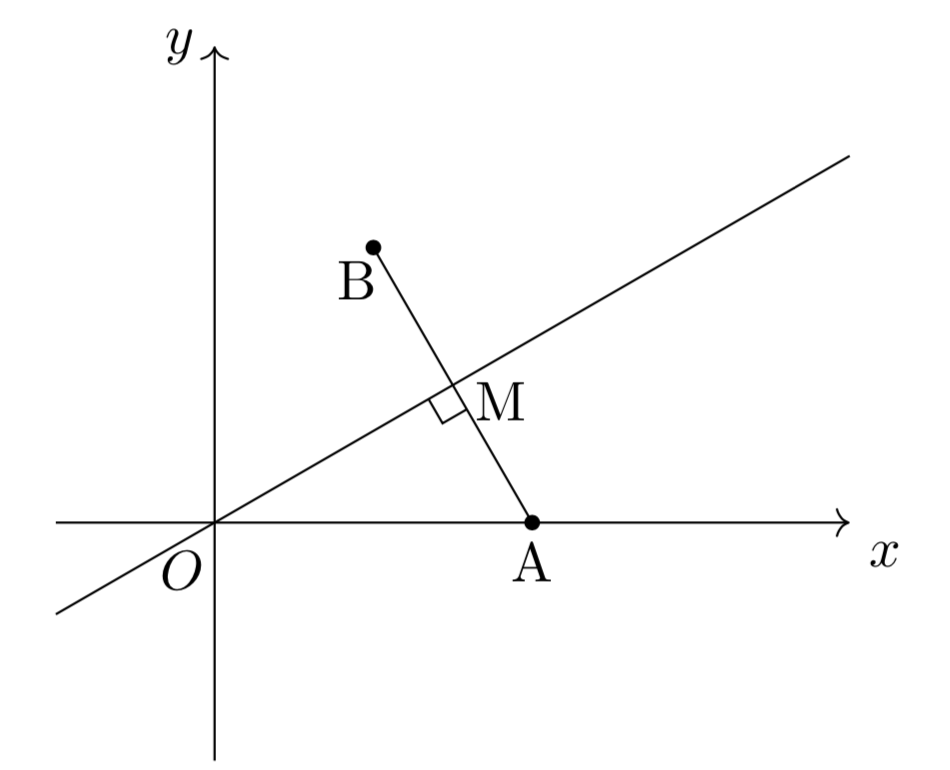
線分ABの中点をMとすれば、$\angle\mathrm{OMA}=\frac{\pi}{2}$が常に成り立っているので、上でも用いた図形的考察から点Mは線分OAを直径とする円のうち、原点Oを除いた部分を動くことがわかります。
今求めたいのは点Bの軌跡なので、「線分ABの中点が線分OAを直径とする円のうち、原点Oを除いた部分を動く」という条件を考えることで答えにたどり着けます。
以下、解答例です。
線分ABの中点をMとすれば、$\angle\mathrm{OMA}=\frac{\pi}{2}$が常に成り立っていることから、点Mは線分OAを直径とする円周上を動く。
ただし、$y=mx$が$y$軸に平行になることはないので、点Mの軌跡は、
\[(x-1)^2+y^2=1 ((x,\,y)\ne (0,\,0))\]
となる。ここで、点B$(X,\,Y)$とすれば、線分ABの中点は、
\[\left(\frac{X+2}{2},\,\frac{Y}{2}\right)\]
となるので、$x=\frac{X+2}{2},\,y=\frac{Y}{2}$を上の軌跡の式に代入して、
\[\begin{align*}&\left(\frac{X+2}{2}-1\right)^2+\left(\frac{Y}{2}\right)^2=1\\\Leftrightarrow & X^2+Y^2=4\end{align*}\]
\[\left(\frac{X+2}{2},\,\frac{Y}{2}\right)\ne (0,\,0)\Leftrightarrow (X,\,Y)\ne(-2,\,0)\]
したがって、求める軌跡は、
\[\boldsymbol{x^2+y^2=4 ((x,\,y)\ne (-2,\,0))}\]
中点Mの軌跡を求めるときには図形的考察を用いて、そのあと点Bの軌跡を求めるときには代数的に処理しているのがこの問題の特徴でしょう。
動画にすると以下のように動いているのが見えます。

問題3
点$\mathrm{O}$を原点とし、放物線$C:y=\sqrt{3}x^2$上に2点$\mathrm{P},\,\mathrm{Q}$を$\angle\mathrm{POQ}=\frac{\pi}{2}$となるようにとる。$\mathrm{P},\,\mathrm{Q}$が$C$上を自由に動くとき、線分$\mathrm{PQ}$の中点$\mathrm{R}$の軌跡を求めよ。
解答・解説
P、Qの対称性を意識すると、2点P、Qの$x$座標をパラメータとして、点Rの座標を表すことになります。
あとは、$\angle\mathrm{POQ}=\frac{\pi}{2}$という条件を数式で表し、パラメータの消去をするだけです。
また、2つのパラメータは対称になっているので、基本対称式の置き換えをすると見通しがよくなります。$s,\,t$の実数条件を反映させ忘れないように気をつけましょう。
以下、解答例になります。
題意より、実数$s,t(s\ne0,\,t\ne 0)$を用いて、$\mathrm{P}(s,\,\sqrt{3}s^2)$、$\mathrm{Q}(t,\,\sqrt{3}t^2)$と表せる。このとき、点$\mathrm{R}(X,\,Y)$は、
\[\left\{\begin{array}{l}X=\frac{s+t}{2}\\Y=\frac{\sqrt{3}(s^2+t^2)}{2}\end{array}\right.\]
と表せる。
また、$\angle\mathrm{POQ}=\frac{\pi}{2}$が成り立つから、
\[\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}=0\Leftrightarrow st+3s^2t^2=0\]
が言える。
ここで、$u=s+t,\,v=st$とおくと、$s,\,t$は$p$の2次方程式$p^2-up+v=0$の2解であるから、$s,\,t$が0でない実数であることは、この2次方程式が0でない2実数解(重解を含む)を持つことと同値で、
\[v\ne 0かつu^2-4v\geqq 0\]
また、$u=s+t,\,v=st$より、
\[\begin{align*}&\left\{\begin{array}{l}X=\frac{u}{2}\\Y=\frac{\sqrt{3}(u^2-2v)}{2}\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}u=2X\\Y=\sqrt{3}(2X^2-v)\end{array}\right.\end{align*}\]
となる。さらに、$st+3s^2t^2=0$は、$v\ne 0$も考慮すると、
\[v+3v^2=0\Leftrightarrow v=-\frac{1}{3}\]
と変形できる。
$Y=\sqrt{3}(2X^2-v)$に$v=-\frac{1}{3}$を代入して、
\[Y=2\sqrt{3}X^2+\frac{\sqrt{3}}{3}\]
また、$u^2-4v\geqq 0$に$u=2X$と$v=-\frac{1}{3}$をそれぞれ代入して、
\[4X^2+\frac{4}{3}\geqq 0\]
これは常に成立する。以上より、求める軌跡は、
\[\boldsymbol{y=2\sqrt{3}x^2+\frac{\sqrt{3}}{3}}\]
今回は、自分で座標設定をして、それが消去すべきパラメータとなります。基本対称式を文字でおいたときには、元の文字の実数条件を反映させなければいけないことに注意しましょう。
まとめ
・軌跡の問題の解き方はパラメータの消去と図形的考察の2パターン
・パラメータを消去するときにはすべての条件に代入することを忘れない!
・図形的考察では「ある線分の両端から見て常に直角ならばその線分を直径とする円周上を動く」というのを使うことが多い
・図形的考察では、軌跡のうち通らない範囲がないかに細心の注意を払う!