この記事を読むとわかること
・正射影ベクトルがどういうものか
・平面における直線の上への正射影ベクトルの公式
\[\frac{\vec{a}\cdot\vec{l}}{|\vec{l}^2|}\vec{l}\]
・空間における平面の上への正射影ベクトルの公式
\[\vec{a}-\frac{\vec{a}\cdot\vec{n}}{|\vec{n}|^2}\vec{n}\]
・ 正射影ベクトルを知っていると簡単に解ける入試問題
正射影ベクトルとは?
正射影ベクトルとはベクトルに光を当てた時の影のベクトル
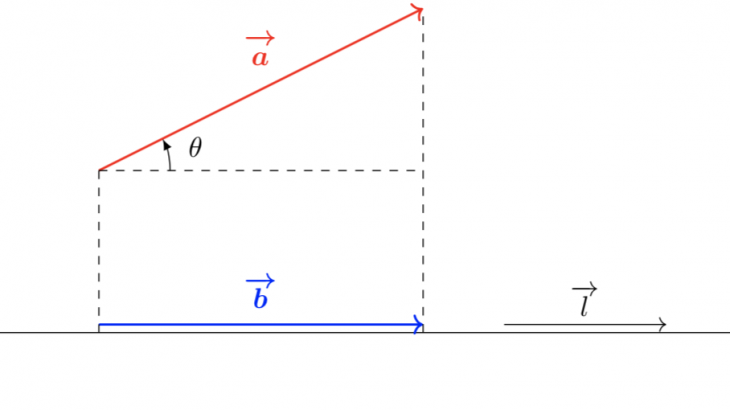
正射影ベクトルとは、簡単に言えば、「ベクトルに対して光を当てた時に出てくる、影となるベクトルのこと」を指します。
影ができるときには、物体も必要ですが、それが映るスクリーンも必要ですよね。よって、正射影ベクトルを定義するには、元のベクトルと、スクリーンになるベクトルの2つを指定する必要があります。
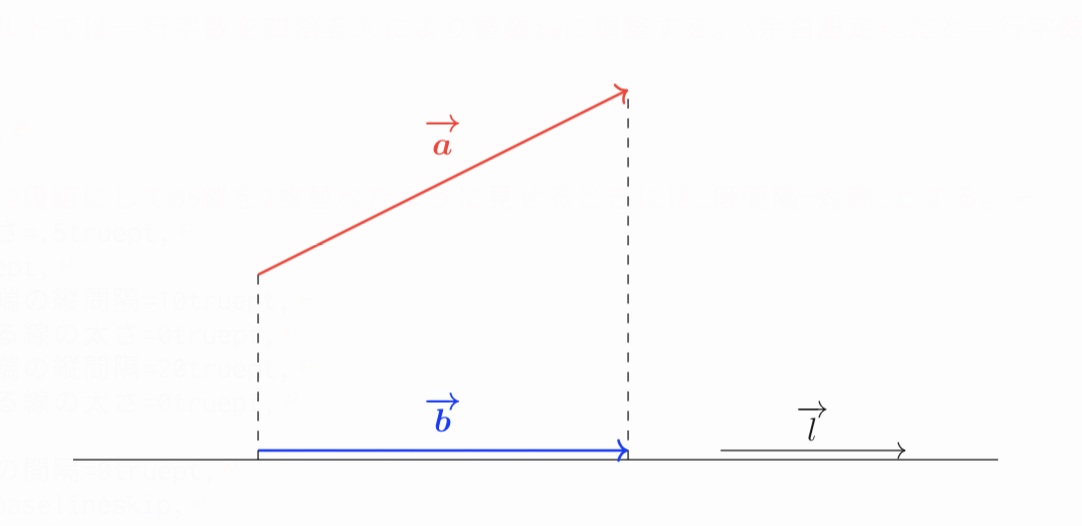
下図では$\vec{a}$が元のベクトル、$\vec{l}$がスクリーンとなるベクトルに対応し、$\vec{b}$は「$\vec{a}$の$\vec{l}$の上への正射影ベクトル」を表しています。
正射影ベクトルは高校では習わないが便利な道具
正射影ベクトルは、実は高校では習わないことが多いんですが、公式を知っておくだけで入試問題を解くのに非常に役立つ便利な道具です。
そこで、この記事では、平面における正射影ベクトルの公式、空間における正射影ベクトルの公式の2つを紹介してから、正射影ベクトルの公式の使い方・便利さを確かめるべく、公式を使うことによって解くのが楽になる問題を2題紹介したいと思います。
正射影ベクトルの公式は?
正射影ベクトルの公式をまずは学びましょう!正射影ベクトルの公式には実は2種類あって、平面の正射影ベクトルの公式と空間での正射影ベクトルの公式があります。
前者の方が重要度は圧倒的に高いんですが、後者も覚えておいて損はないでしょう。
平面の正射影ベクトルの公式(直線への正射影ベクトル)
$\vec{a}$の$\vec{l}$の上への正射影ベクトルは、
\[\frac{\vec{a}\cdot\vec{l}}{|\vec{l}^2|}\vec{l}\]
で表される。
この公式を証明していきましょう。
平面の正射影ベクトルの公式の証明
正射影ベクトルの公式の証明は難しくありません。よって、公式を万が一忘れてしまった場合でも、その場で導出することによって対応が可能です。
下図のように向き付きの角度$\theta$を定めると、内積の定義より、
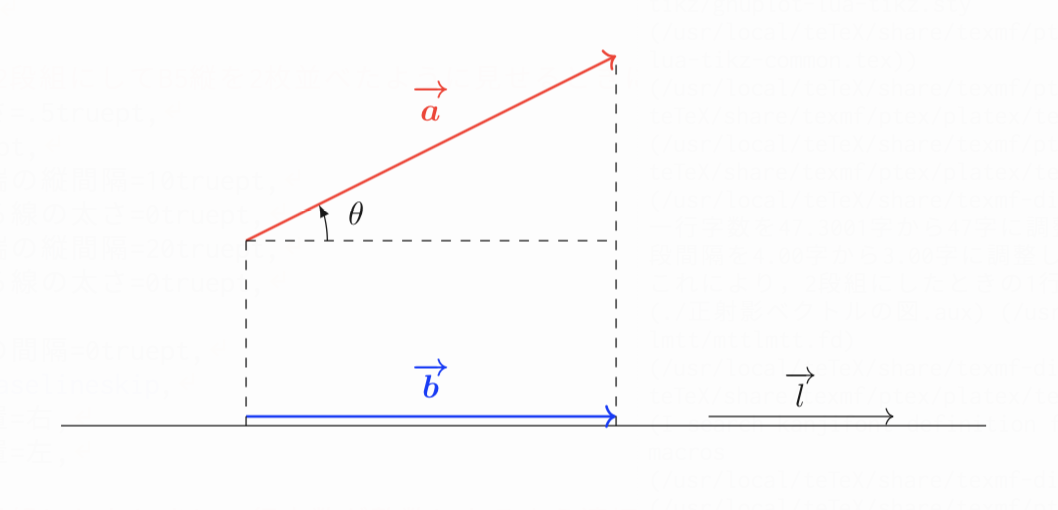
\[ \cos{\theta}=\frac{\vec{a}\cdot\vec{l}}{|\vec{a}||\vec{l}|}\]
なので、正射影ベクトルの長さ(正射影ベクトルの向きが$\vec{l}$と逆向きのときはマイナスの値を取る)は、
\[\vec{a}\cos{\theta}=\frac{\vec{a}\cdot\vec{l}}{|\vec{l}|}\]
となる。求める$\vec{l}$に平行な単位ベクトルは$\frac{\vec{l}}{|\vec{l}|}$であるので、求める正射影ベクトルは、
\[\frac{\vec{a}\cdot\vec{l}}{|\vec{l}|}\cdot\frac{\vec{l}}{|\vec{l}|}=\frac{\vec{a}\cdot\vec{l}}{|\vec{l}|^2}\vec{l}\]
となる。
単位ベクトルの上への正射影の場合の公式
もし、$\vec{l}$が単位ベクトル(長さが1のベクトル)$\vec{e}$だった場合には正射影ベクトルの公式は、
\[(\vec{a}\cdot\vec{e})\vec{e}\]
となり、非常にシンプルな式になります。
空間の(平面への)正射影ベクトルの公式
先ほどは、平面における正射影ベクトルの公式について扱いましたが、当然空間における公式も存在します。
$\vec{a}$の、「$\vec{n}$を法線ベクトルとする平面」の上への正射影ベクトルは、
\[\vec{a}-\frac{\vec{a}\cdot\vec{n}}{|\vec{n}|^2}\vec{n}\]
こちらは、高校数学で全く扱わない事項であるため、説明なしに大学受験の答案で使用するのは控えておいた方がよいでしょう。
空間の正射影ベクトルの公式の証明
こちらの証明は、平面での正射影ベクトルの公式がすでにわかっていれば一瞬で証明できます。解答で使うときには以下のように説明をしてから使うとよいでしょう。
$\vec{a}$の$\vec{n}$への正射影ベクトルは、
\[\frac{\vec{a}\cdot\vec{n}}{|\vec{n}|^2}\vec{n}\]
であるから、求めるベクトルは下図より、
\[\vec{a}-\frac{\vec{a}\cdot\vec{n}}{|\vec{n}|^2}\vec{n}\]
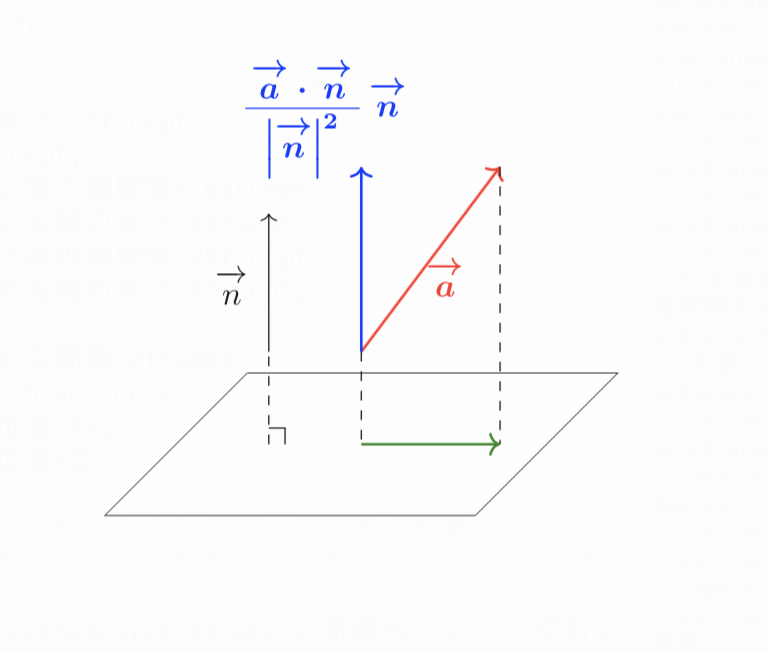
平面での正射影ベクトルの公式を使って、$\vec{a}$の平面に垂直な成分を求めてそれを除いてあげれば求めたいベクトルが求まるというわけですね!
正射影ベクトルを使う入試問題
公式を覚えたら実際に正射影ベクトルを使う入試問題を解いてみましょう。ここでは、正射影ベクトルを用いる基本問題を1題、入試問題を1題紹介しようと思います。
正射影ベクトルを用いる基本問題
$\mathrm{OA}=4,\,\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=3$を満たす三角形$\mathrm{OAB}$において、点$\mathrm{B}$から直線$\mathrm{OA}$に下ろした垂線の足を$\mathrm{P}$とする。
$\overrightarrow{\mathrm{OP}}$を$k\overrightarrow{\mathrm{OA}}$($k$は実数)の形で表せ。
解答
$\overrightarrow{\mathrm{OP}}$は、$\overrightarrow{\mathrm{OB}}$の$\overrightarrow{\mathrm{OA}}$の上への正射影ベクトルに等しいから、
\[\overrightarrow{\mathrm{OP}}=\frac{\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}}{\left|\overrightarrow{\mathrm{OA}}\right|^2}\overrightarrow{\mathrm{OA}}=\frac{3}{16}\overrightarrow{\mathrm{OA}}\]
$\mathrm{OB}$の長さが与えられていないので、三角形の形を決定できないものの、その正射影は一定であるので、答えを求めることができるのが面白いですね。
正射影ベクトルを用いる応用問題
空間において、$\mathrm{O}$を原点、$\mathrm{P}$を平面$\pi$上の点、$\vec{a}$を$\pi$に垂直な零でないベクトルとする。空間の任意の点を$\mathrm{Q}$とする。$\pi$に関して$\mathrm{Q}$と対称な点を$\mathrm{Q’}$とするとき、$\overrightarrow{\mathrm{OQ’}}$を$\overrightarrow{\mathrm{OP}},\,\overrightarrow{\mathrm{OQ}},\,\vec{a}$を用いて表せ。(関西学院大学・商学部)
解答
線分$\mathrm{QQ’}$の中点を$\mathrm{M}$とすると、$\overrightarrow{\mathrm{QM}}$は$\overrightarrow{\mathrm{OP}}$の$\vec{a}$の上への正射影ベクトルに等しいから、
\[\overrightarrow{\mathrm{QM}}=\frac{\overrightarrow{\mathrm{QP}}\cdot\vec{a}}{|\vec{a}|^2}\vec{a}=\frac{\left(\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OQ}}\right)\cdot\vec{a}}{|\vec{a}|^2}\vec{a}\]
また、$\overrightarrow{\mathrm{QQ’}}=2\overrightarrow{\mathrm{QM}}$であるので、
\[\overrightarrow{\mathrm{OQ’}}=\overrightarrow{\mathrm{OQ}}+2\overrightarrow{\mathrm{QM}}=\overrightarrow{\mathrm{OQ}}+2\frac{\left(\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OQ}}\right)\cdot\vec{a}}{|\vec{a}|^2}\vec{a}\]
空間図形の問題であり、少し戸惑う人も多いと思いますが、平面において直線に関して対称な点を求める際に正射影ベクトルの公式を用いるのと何ら変わりません。
これは、平面も空間もほとんど同様に扱えるというベクトルの強みがわかるところですね。
まとめ
正射影ベクトルは、それを知っておくだけで、入試問題を解くスピードが非常にはやくなることがわかったと思います。公式を覚えておいて、他の受験生と差をつけましょう!