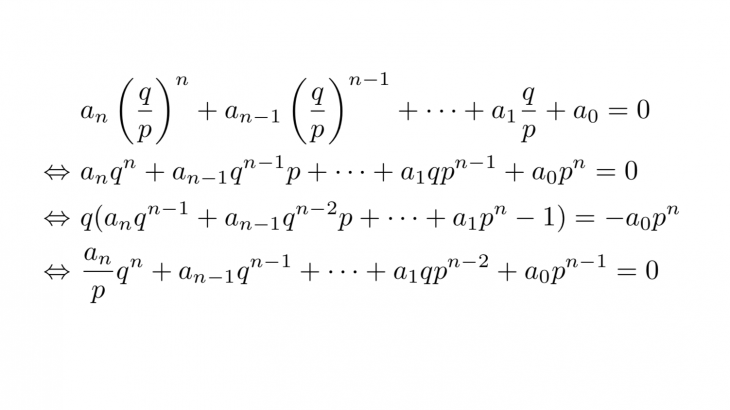この記事を読むとわかること
・有理数解とはそもそも何か
・有理数解や整数解に関わる定理
・有理数解を持つ/持たないが関わる入試問題
方程式の有理数解
そもそも有理数解とは
有理数解とは、方程式の解のうち、2つの整数の分数の形で表せるようなもののことです。
入試問題ではしばしば、「この方程式が有理数解を持つような条件を求めよ」というような形式の問題が出題されることがあります。
こういった問題を解くためには、有理数解についての定理を知っておく必要があります。この記事では有理数解についての重要な定理について書いてから、その定理を用いて解ける問題をいくつか紹介したいと思います。
有理数解や整数解に関わる重要な定理
高校数学において、有理数解に関わる重要な定理はこの1つだけです。
整数係数の$n$次方程式$a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0=0(a_n\ne 0,\,a_0\ne 0)$が有理数解を持つとすれば、それは、
\[\frac{a_0の約数}{a_nの約数}\]
の形のものに限られる。
例えば、3次方程式$3x^3+2x^2+x+4=0$があったとすれば、有理数解は、
\[x=\pm1,\,\pm2,\,\pm4,\,\pm\frac{1}{3},\,\pm\frac{2}{3},\,\pm\frac{4}{3}\]
の12個に限られるということですね!
さらに、有理数解ではなく、整数解を持つ場合にはさらに強い条件が言えます。
整数係数の$n$次方程式$a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0=0(a_n\ne 0,\,a_0\ne 0)$が整数解を持つとすれば、それは、$a_0$の約数に限られる。
整数解があるとすれば、$x$を含む項はすべてその整数解で割り切れるので、定数項がその整数解で割り切れる必要があることからすぐにわかりますね。先ほどの定理で分母が$1$になると思っておけば覚えやすいでしょう。
定理の証明
さて、有理数解の候補がこのように限られるのはどのように証明すればよいのでしょうか?この定理は、高校数学では一応示してから使うことになるので、証明の流れは必ず覚えておきましょう。
整数係数の$n$次方程式$a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0=0(a_n\ne 0,\,a_0\ne 0)$が有理数解を持つとき、その有理数解は$\frac{q}{p}(pは自然数、qはpと互いに素な整数)$とおける。これを代入すると、
\[\begin{align*}&a_n\left(\frac{q}{p}\right)^n+a_{n-1}\left(\frac{q}{p}\right)^{n-1}+\cdots +a_1\frac{q}{p}+a_0=0\\\Leftrightarrow &a_nq^n+a_{n-1}q^{n-1}p+\cdots +a_1qp^{n-1}+a_0p^n=0\\\Leftrightarrow &q(a_nq^{n-1}+a_{n-1}q^{n-2}p+\cdots +a_1p^n-1)=-a_0p^n\end{align*}\]
ここで、$p$と$q$は互いに素であるから、$q$は$a_0$の約数であることが分かる。
また、
\[\frac{a_n}{p}q^n+a_{n-1}q^{n-1}+\cdots +a_1qp^{n-2}+a_0p^{n-1}=0\]
と変形することもできるので、$p$と$q$は互いに素であることも考慮すると、$\frac{a_n}{p}$が整数である必要がある。つまり$p$は$a_n$の約数。
以上より、有理数解は
\[\frac{a_0の約数}{a_nの約数}\]
の形のものに限られることが示された。
$p$や$q$を1個だけ残すような操作をすれば簡単に証明ができるわけですね。
有理数解を持つ/持たないが出てくる入試問題3選
この定理を用いて、「有理数を持つ/持たない」が関わるような入試問題を3つ紹介したいと思います!
問題1
$x^3+kx^2+7=0(kは整数)$が有理数解を持つときそれは整数解に限られることを示せ。また、正の整数解をもつときの$k$をすべて求めよ。
解答・解説
有理数解に関する定理において、分母が$\pm 1$に限られるパターンです。定理の証明を具体的な方程式に適用してあげるだけで良さそうです。あとは、正の整数解の候補をすべて代入していけば答えが求まります。
有理数解は$\frac{q}{p}(pは自然数、qはpと互いに素な整数)$とおける。これを代入すると、
\[\begin{align*}&\left(\frac{q}{p}\right)^3+\left(\frac{q}{p}\right)^2+7=0\\\Leftrightarrow &\frac{q^3}{p}+kq^2+7p^2=0\end{align*}\]
右辺は整数で、$kq^2+7p^2$も整数であるから、$\frac{q^3}{p}$も整数である必要がある。$p,\,q$が互いに素であることも考慮すると、$p=1$
したがって、有理数解を持つならば整数解しかありえないことが示された。
正の有理数解を持つとすると、それは正の整数解であり、それを$\alpha$とおくと、
\[\alpha^3+k\alpha^2+7=0\Leftrightarrow \alpha(\alpha^2+k\alpha)=-7\]
より、$\alpha$は$7$の約数であることがわかる。よって、$\alpha=1,\,7$
$\alpha=1$のとき、
\[1+k+7=0\Leftrightarrow k=-8\]
$\alpha=7$のとき、
\[343+49k+7=0\Leftrightarrow k=\frac{50}{7}\]
これは整数でないので不適。
以上より、
\[\boldsymbol{k=-8}\]
問題2
$3x^3+2x+4=0$が有理数解を持たないことを示せ。
解答
「有理数解を持たないこと」を示すには、有理数解の候補をすべて代入して成り立たないことが言えればOKです。有理数解を持つと仮定して矛盾を導く背理法になっています。まずは、定理の証明と同じ流れを辿って有理数解の候補をすべて調べあげましょう。
$3x^3+2x+4=0$が有理数解を持つと仮定すると、それは$\frac{q}{p}(pは自然数、qはpと互いに素な整数)$とおける。これを代入すると、
\[\begin{align*}&3\left(\frac{q}{p}\right)^3+2\frac{q}{p}+4=0\\\Leftrightarrow &q(3q^2+2p^2)=-4p^3\end{align*}\]
$p,\,q$は互いに素であるから、$q$は$4$の約数である必要があり、$q=\pm 1,\,\pm 2,\,\pm 4$
また、
\[\begin{align*}&3\left(\frac{q}{p}\right)^3+2\frac{q}{p}+4=0\\\Leftrightarrow &\frac{3}{p}q^3+2qp+4p^2=0\end{align*}\]
と変形することもできて、$2qp+4p^2$は整数であるから、$\frac{3}{p}q^3$も整数であり、$p,\,q$は互いに素であることも考慮すると、$p$は$3$の約数となる。よって、$p=1,\,3$
したがって、与えられた方程式の有理数解の候補は、
\[\pm 1,\,\pm 2,\,\pm 4,\,\pm\frac{1}{3},\,\pm\frac{2}{3},\,\pm\frac{4}{3}\]
の12個に限られるが、これらはすべて与えられた方程式を満たさない。
以上より、与えられた方程式は有理数解を持たないことが示された。
代入する個数が多いですが、有理数解を持たないことを示す問題なので、実際に計算しなくても、「与えられた方程式を満たさない」とだけ書いておけば大丈夫ですね。
問題3
$5x^3+8x^2-14x+4=0$を解け。
解答
ただ3次方程式を解くだけじゃん!と思われてしまいますが、これが意外と難しいんです。3次方程式を解くときは整数解がないか探して因数分解をするのが基本ですが、いろんな整数を代入してもどれも成り立ちません。
そこで、今回習った定理を活かして整数解ではなく可能性のある有理数解をいろいろ代入してみることになります。そうすると、$\frac{2}{5}$が解の1つとなることがわかり、あとは因数分解をするだけです!
解答を書くのは非常に短いですが、整数解でない有理数解を探す作業は意外と骨の折れる作業です…!
\[\begin{align*}&5x^3+8x^2-14x+4=0\\\Leftrightarrow &(5x-2)(x^2+2x-2)=0\\\Leftrightarrow &\boldsymbol{x=\frac{2}{5},\,-1\pm\sqrt{3}}\end{align*}\]
まとめ
・整数係数の方程式の有理数解は、
\[\frac{a_0の約数}{a_nの約数}\]
の形のものに限られる
・整数解の場合は定数項の約数に限られる
・有理数解を文字で置いて、それぞれ1文字を残すような式変形をすると証明できる