※以下の解答・解説は当ブログのオリジナルのものであり東京大学が公表しているものではありません。
私がおすすめする過去問題集について説明した記事はこちら↓
第一問
第一問は以下のような問題でした。
第一問の難易度分析
微分をして増減表を描き、極限を調べる問題です。
微分したあとに式を整理していくと符号のよくわからない因数がでてきます。そこで、その部分だけもう一度微分して、符号の変化がどうなるかを調べることになります。
微分と極限の基礎知識が身についていれば容易に満点が取れる非常に易しい問題だと言えるでしょう。ぜひとも完答したいところです。
第一問を解く上での考え方・ポイント
三角関数や分数関数の微分公式を覚えていれば微分できますね。忘れがちな分数関数の微分について復習しておきましょう。
分数関数の微分公式
\[\left\{\frac{f(x)}{g(x)}\right\}’=\frac{f'(x)g(x)-g'(x)f(x)}{\{g(x)\}^2}\]
そのあと整理していくと、符号のわからない因数が出てくるので、その部分だけ取り出してもう一度微分することになります。
微分して符号のわからない因数が出てきたらその部分をもう一度微分する!
\[\begin{align*}f'(x)=&\frac{\sin x-x\cos x}{\sin^2 x}-\sin x\\=&\frac{\sin x-\sin^3 x-x\cos x}{\sin^2 x}\\=&\frac{\sin x(1-\sin^2x)-x\cos x}{\sin^2 x}\\=&\frac{\sin x\cos^2x-x\cos x}{\sin^2 x}\\=&\frac{\cos x(\sin x\cos x-x)}{\sin^2 x}\end{align*}\]
ここで、$g(x)=\sin x\cos x-x=\frac{1}{2}\sin 2x-x$とおくと、
\[g'(x)=\cos 2x -1<0\]
よって$g(x)$は単調減少するので、
\[g(x)<g(0)=0\]
がわかる。つまり、$f'(x)$の符号は$\frac{-\cos x}{\sin^2 x}$の符号に一致する。したがって、増減表は以下のようになる。
\[ \begin{array}{|c||c|c|c|c|c|} \hline x & (0) & \cdots & \frac{\pi}{2} & \cdots & (\pi) \\ \hline f'(x) & & – & 0 & + & \\ \hline f(x) & & \searrow & \frac{\pi}{2} & \nearrow & \\ \hline \end{array} \]
増減表が描けたらあとは極限を求めるだけです!
高校数学では極限公式は以下の3つを覚えていれば他のどの公式も簡単に導くことができます。
高校数学で覚えておくべき極限公式3つ!
\[\lim_{x\to 0}\frac{\sin x}{x}=1\]
\[\lim_{x\to 0}\frac{e^x-1}{x}=1\]
\[\lim_{x\to \infty}\left(1+\frac{1}{x}\right)^x=e\]
これらの極限公式のどれを使えばいいか考えながら解けば極限も簡単に求まります。
極限公式で使えそうなのは\[\lim_{x\to 0}\frac{\sin x}{x}=1\]なので、$x\rightarrow \pi-0$のときは、変数の置き換えをして$x\rightarrow +0$としてあげればよさそうです。解答例は以下のようになります。
\[\lim_{x\to 0}\frac{\sin x}{x}=1\]であることから、
\[\lim_{x\to +0}\left(\frac{x}{\sin x}+\cos x\right)=\boldsymbol{2}\]
また、$x\rightarrow \pi-0$のとき、$t=\pi -x$とすれば、
\[\begin{align*}&\lim_{x\to\pi-0}\frac{x}{\sin x}+\cos x\\=&\lim_{t\to +0}\frac{\pi-t}{\sin (\pi-t)}+\cos(\pi-t)\\=&\lim_{t\to +0}\frac{t}{\sin t}-\frac{t}{\sin t}-\cos t\rightarrow \boldsymbol{\infty}\end{align*}\]
特に躓くところなく解ける問題でしょう。
第二問
第二問は以下のような問題でした。

第二問の難易度分析
非常に易しい整数問題です。コンビネーションの定義、ユークリッドの互除法を覚えていれば解けるようになっています。東大ではこれほど易しい整数問題が出ることはなかなかないのではないかと思います。必ず完答したいところでしょう。
第二問(1)を解く上での考え方・ポイント
まずは、コンビネーションの定義
\[_nC_r=\frac{n!}{(n-r)!r!}\]
を覚えていれば、$\frac{a_n}{a_{n-1}}$を求めることができます。
約分をすると、
\[\frac{a_n}{a_{n-1}}=\frac{2(2n+1)}{n(n+1)}\]
となりますが、これが既約分数なのかどうか判定する必要が出てきます。そこで、ユークリッドの互除法を思い出しましょう。
ユークリッドの互除法
2つの自然数$a,\,b(a\geqq b)$に対して、$a$と$b$の最大公約数は$a$を$b$で割ったときのあまりを$r$とすれば$b$と$r$の最大公約数に等しい。
\[2n+1=2\cdot n+1\]
に着目すれば、2数の最大公約数が1、つまり2数が互いに素であることが示せます。同様にして、
\[2n+1=1\cdot(n+1)+n\]
\[n+1=1\cdot n+1\]
となるので、こちらも互いに素であることが示せます。あとは簡単ですね。以下に解答例を示しておきます。
\[\begin{align*}\frac{a_n}{a_{n-1}}=&\frac{\frac{_{2n+1}C_{n}}{n!}}{\frac{_{2n-1}C_{n-1}}{(n-1)!}}\\=&\frac{1}{n}\cdot\frac{(2n+1)!}{(n+1)!n!}\cdot\frac{(n-1)!n!}{(2n-1)!}\\=&\frac{2(2n+1)}{n(n+1)}\end{align*}\]
ここで、
\[2n+1=2\cdot n+1\]
より、ユークリッドの互除法から$2n+1$と$n$は互いに素であることが分かる。同様にして、
\[2n+1=1\cdot(n+1)+n\]
\[n+1=1\cdot n+1\]
より、$2n+1$と$n+1$も互いに素である。
また、連続整数の積は常に2の倍数であることから、$n(n+1)$は$2$で約分できる。したがって、
\[\left\{\begin{array}{l}\boldsymbol{p_n=\frac{1}{2}n(n+1)}\\\boldsymbol{q_n=2n+1}\end{array}\right.\]
第二問(2)を解く上での考え方・ポイント
(1)が解けたら、$\frac{q_n}{p_n}$が整数でないときに、$a_n$が整数でなくなるのではないかと予想が少しつきます。しかしながら、
\[a_n=\frac{q_n}{p_n}\cdot\frac{q_{n-1}}{p_{n-1}}\cdot\cdots\cdot\frac{q_2}{p_2}a_1\]
において、$p_n$が$\frac{q_{n-1}}{p_{n-1}}\cdot\cdots\cdot\frac{q_2}{p_2}a_1$で約分できる可能性を排除できないので、その論理ではダメですよね。
そこで、既約分数にしたことによって、分子が常に奇数であることに注目します。よって、分母に偶数が一定数以上出てくれば、整数でないことが簡単に示せそうです。
これを踏まえて、解答例を以下に示します。
$a_1=3,\,a_2=5$であるので、$a_1,\,a_2$は整数である。
ここで、$n\geqq 3$のとき、
\[a_n=\frac{q_n}{p_n}\cdot\frac{q_{n-1}}{p_{n-1}}\cdot\cdots\cdot\frac{q_2}{p_2}a_1\]
が成り立ち、(1)より$q_2,\,\cdots,\,q_n$は奇数、$a_1$も奇数、$p_3(=6)$は偶数であるから、これは整数になりえない。
したがって、$a_n$が整数になるのは、$\boldsymbol{n=1,\,2}$のとき。
第三問
第三問は以下のような問題でした。

第三問の難易度分析
軌跡・領域を面積と絡めた問題です。後半では極限についても問われています。
点が動くのでそれぞれをパラメータで表してから、領域を求めることになります。今回は領域自体を求める必要はなく、面積だけを求めればよいので、$x$か$y$で固定すればよいだけなんですが、受験生は文字固定の議論が苦手な人が多いので、難しく感じる人が多いのではないでしょうか。
そのため、難易度評価としてはやや難としておきます。
第三問を解く上での考え方・ポイント
まずは、与えられた点をそれぞれパラメータを用いて表しておきます。$\mathrm{P}(t,\,t^2)(-1\leqq t\leqq 1)$、$\mathrm{Q}(u,\,0)(0\leqq u\leqq 1)$とおけば、
\[\overrightarrow{\mathrm{OR}}=\left(\begin{array}{c}ku+\frac{t}{k}\\\frac{t^2}{k}\end{array}\right)\]
と表すことができます。領域を求める必要はなく、面積だけを求めればよいので、$x,\,y$のどちらかを固定したときの線分の長さを求めて、それを積分してあげればよさそうです。今回は$x$の方がパラメータの数が多く、固定をしてからの議論に行き詰まってしまうので、$y$の方を固定することになります。
\[\frac{t^2}{k}=p(0\leqq p\leqq \frac{1}{k})\]
と固定してあげれば、$t=\pm\sqrt{kp}$となるので、$x$の方が$u$の1変数関数になって、取りうる値の範囲を求められますね。$S(k)$を求めるところまでの答案は以下のようになります。
題意より、$\mathrm{P}(t,\,t^2)(-1\leqq t\leqq 1)$、$\mathrm{Q}(u,\,0)(0\leqq u\leqq 1)$とおける。このとき、
\[\overrightarrow{\mathrm{OR}}=\left(\begin{array}{c}ku+\frac{t}{k}\\\frac{t^2}{k}\end{array}\right)\]
となる。
\[\frac{t^2}{k}=p(0\leqq p\leqq \frac{1}{k})\]
と固定すると、
\[t=\pm\sqrt{pk}\]
となる。これを代入して、
\[ku+\frac{t}{k}=ku\pm\sqrt{\frac{p}{k}}\]
つまり、$\overrightarrow{\mathrm{OR}}$の$x$成分の取りうる値の範囲は
\[-\sqrt{\frac{p}{k}}\leqq x\leqq k-\sqrt{\frac{p}{k}},\,\sqrt{\frac{p}{k}}\leqq x\leqq k+\sqrt{\frac{p}{k}}\]
となる。ここで、
\[k-\sqrt{\frac{p}{k}}\geq\sqrt{\frac{p}{k}}\Leftrightarrow \frac{k\sqrt{k}}{2}\geq\sqrt{p}\]
両辺$0$以上なので、$2$乗しても同値で、
\[\frac{k^3}{4}\geqq p\]
したがって、$\frac{k^3}{4}\geqq p$ のときは、$x$の取りうる値の範囲は、
\[-\frac{\sqrt{p}}{k\sqrt{k}}\leqq x\leqq k+\frac{\sqrt{p}}{k\sqrt{k}}\]
となり、$\frac{k^3}{4}\leqq p$のときは、$x$の取りうる値の範囲は、
\[-\sqrt{\frac{p}{k}}\leqq x\leqq k-\sqrt{\frac{p}{k}},\,\sqrt{\frac{p}{k}}\leqq x\leqq k+\sqrt{\frac{p}{k}}\]
となる。
$k>0$であることより、
\[\frac{k^3}{4}\geqq \frac{1}{k}\Leftrightarrow k\geqq \sqrt{2}\]
であるので、
(i)$0<k\leqq \sqrt{2}$のとき、
\[\begin{align*}S(k)=&\int_{0}^{\frac{k^3}{4}}\left(k+2\sqrt{\frac{p}{k}}\right)dp+\int_{\frac{k^3}{4}}^{\frac{1}{k}}2kdp\\=&\left[kp+\frac{4}{3}\sqrt{\frac{p^3}{k}}\right]_{0}^{\frac{k^3}{4}}+[2kp]_{\frac{k^3}{4}}^{\frac{1}{k}}\\=&2-\frac{k^4}{12}\end{align*}\]
(ii)$\sqrt{2}\leqq k$のとき、
\[\begin{align*}S(k)=&\int_{0}^{\frac{1}{k}}\left(k+2\sqrt{\frac{p}{k}}\right)dp\\=&\left[kp+\frac{4}{3}\sqrt{\frac{p^3}{k}}\right]_{0}^{\frac{1}{k}}\\=&1-\frac{4}{3k^2}\end{align*}\]
以上より、
\[S(k)=\left\{\begin{array}{l}\boldsymbol{2-\frac{k^4}{12}(0<k\leqq \sqrt{2}のとき)}\\\boldsymbol{1-\frac{4}{3k^2}(\sqrt{2}\leqq kのとき)}\end{array}\right.\]
場合分けがされているので、極限を取るときはどちらの式を用いればよいのかという点に注意しましょう。極限の部分の解答は以下のようになります。
$k\rightarrow +0$のとき、$0<k\leqq \sqrt{2}$としてよいので、
\[\lim_{k\to +0}S(k)=\lim_{k\to +0}\left(2-\frac{k^4}{12}\right)=\boldsymbol{2}\]
$k\rightarrow \infty$のとき、$\sqrt{2}\leqq k$としてよいので、
\[\lim_{k\to \infty}S(k)=\lim_{k\to \infty}\left(1-\frac{4}{3k^2}\right)=\boldsymbol{1}\]
さて、極限計算をしたら図形的に考えて、検算をしてあげましょう。
$k\overrightarrow{\mathrm{OQ}}$は$y=\frac{1}{k}x^2$の$-k\leqq x\leqq k$の部分を動き、それを$x$軸方向に$\frac{1}{k}$だけ平行移動したものが$\overrightarrow{\mathrm{OR}}$の動く領域なので、$k\to +0$のとき、下図のように、長さ$\frac{1}{k}$の線分が高さ$k$まで積み上げられてできた図形が2つあると見ることができます。
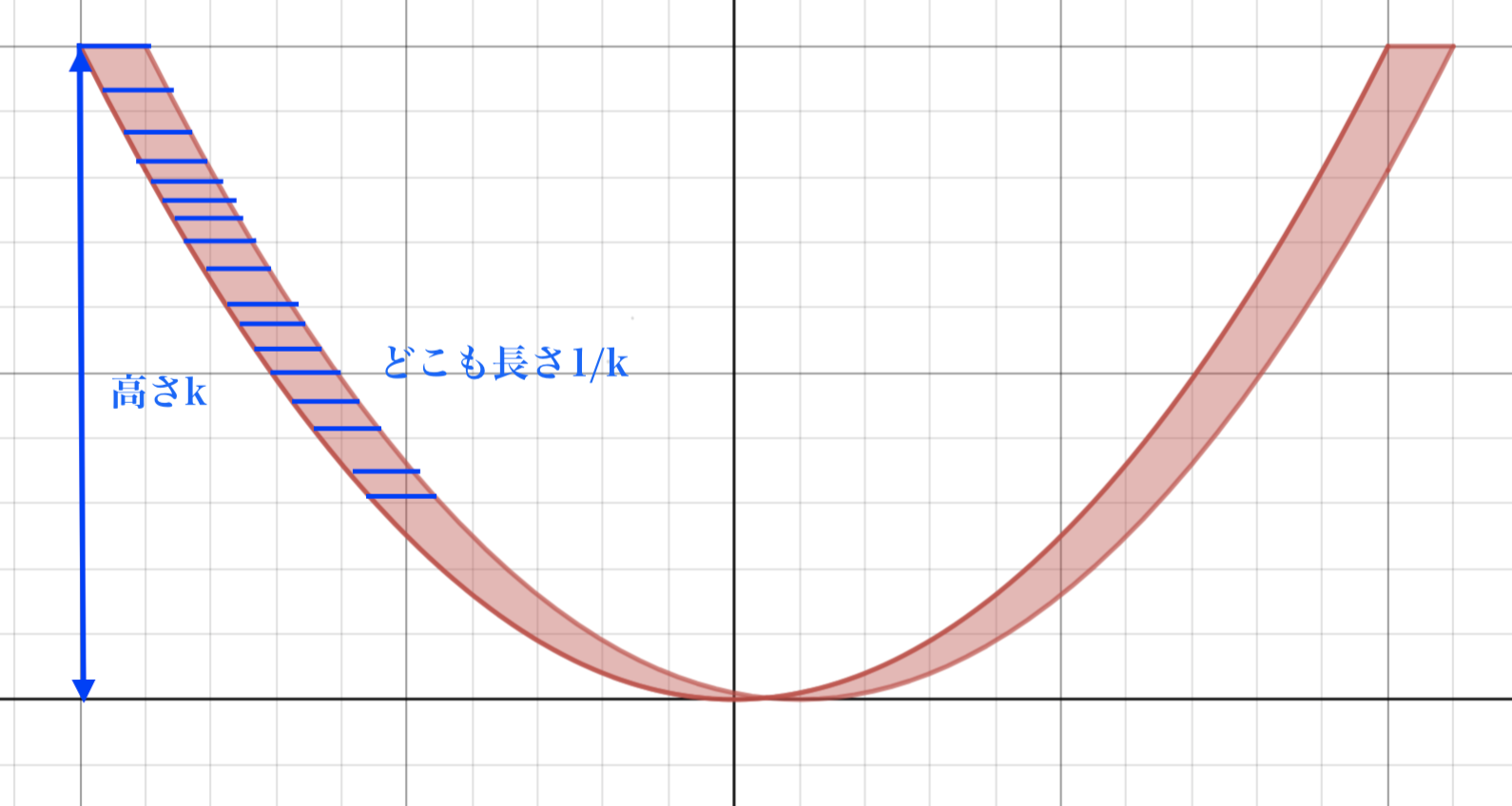
よって、これは面積1の平行四辺形2つの面積に等しいので、極限は$2$になるとわかります。
$k\to\infty$のときは、底辺の長さが$\frac{1}{k}$、高さが$k$の長方形と見ることができます。
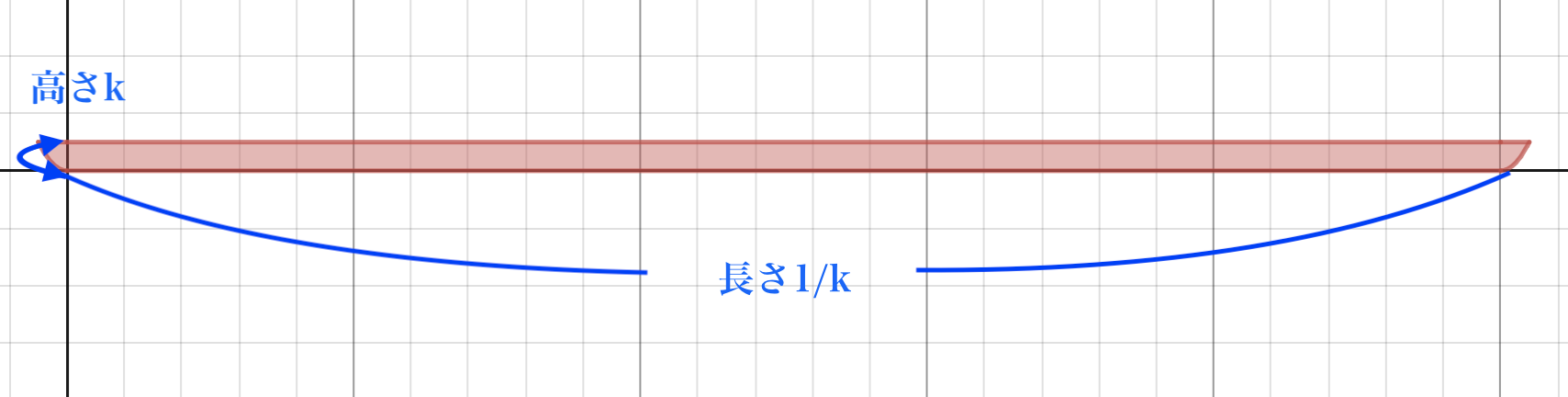
この面積は$1$になるので、極限値は$1$だとわかります。
このようにして、図形的に極限値を予想しておき、それが実際に計算していって求めた極限値と一致しているか確かめることによって、そのまえの計算が正しいかどうかの確認をすることができます。今回の問題のように極限値が問われていない場合でも、極限計算をして積分計算が正しいかどうか確かめる癖をつけておくとよいでしょう。
第四問
第四問は以下のような問題でした。

第四問の難易度分析
非常に易しい解の配置の問題です。3次関数の解の配置のときは、定数分離をして、3次関数が動かないようにするのが基本という点をしっかりと覚えていれば難なく解けたでしょう。
第四問を解く上での考え方・ポイント
解の配置問題の解法は、以下の記事にまとめられています。
今回は、3次以上の関数の解の配置問題なので、定数$b$を分離して、$y=f(x)$と$y=b$の共有点の変化をグラフで考えればいけますね。
2つ目の$\beta>1$という条件は、グラフを見れば、「$1<a$かつ$f(1)>b$」と言い換えられます。特に難しいところはないでしょう。
以下に解答例を示しておきます。
\[f'(x)=3(x-a)(x+a)\]
より、$f(x)$の増減表は以下のようになる。
\[\begin{array}{|c||c|c|c|c|c|}\hline x & \cdots & -a & \cdots & a & \cdots \\\hline f'(x) & + & 0 & – & 0 & + \\\hline f(x) & \nearrow & 2a^3 & \searrow & -2a^3 & \nearrow \\\hline\end{array}\]
よって、グラフは以下。
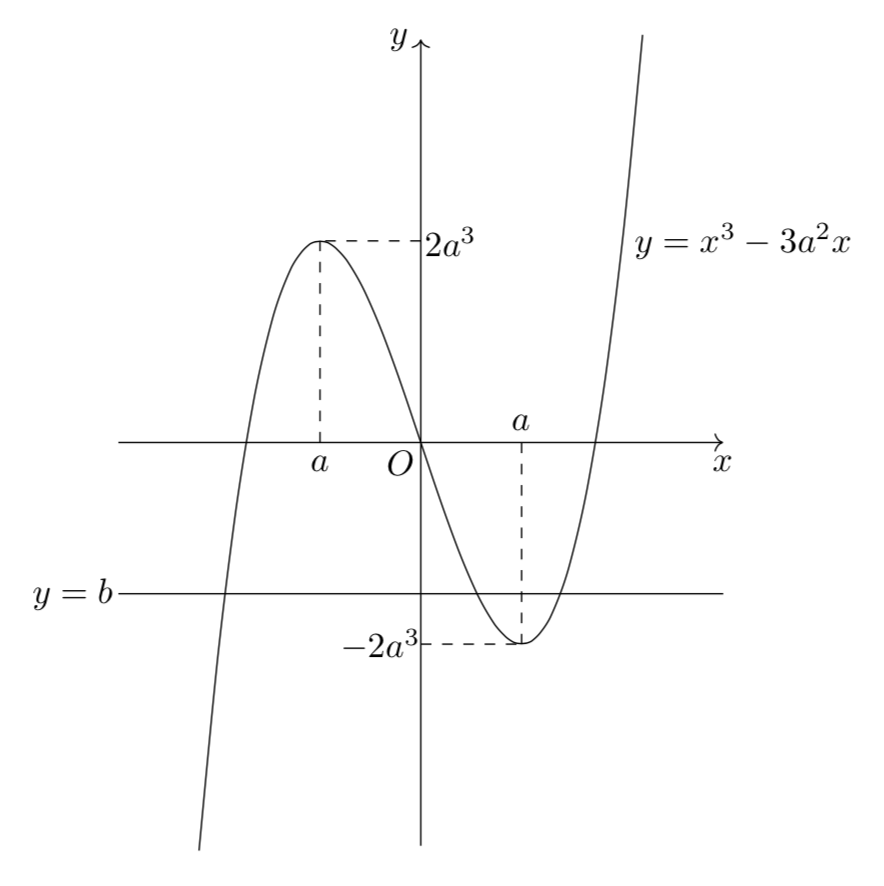
方程式$f(x)=b$は相異なる3実数解をもつことは、$y=f(x)$と$y=b$が相異なる共有点を3つ持つことと同値であるから、
\[条件1\Leftrightarrow -2a^3<b<2a^3\]
また、$\beta>1$となることは、上図より、
\[1<a,\,f(1)>b\Leftrightarrow 1<a,\,1-3a^2>b\]
と同値である。以上より、求める領域は以下のようになる。(ただし境界はすべて含まない)
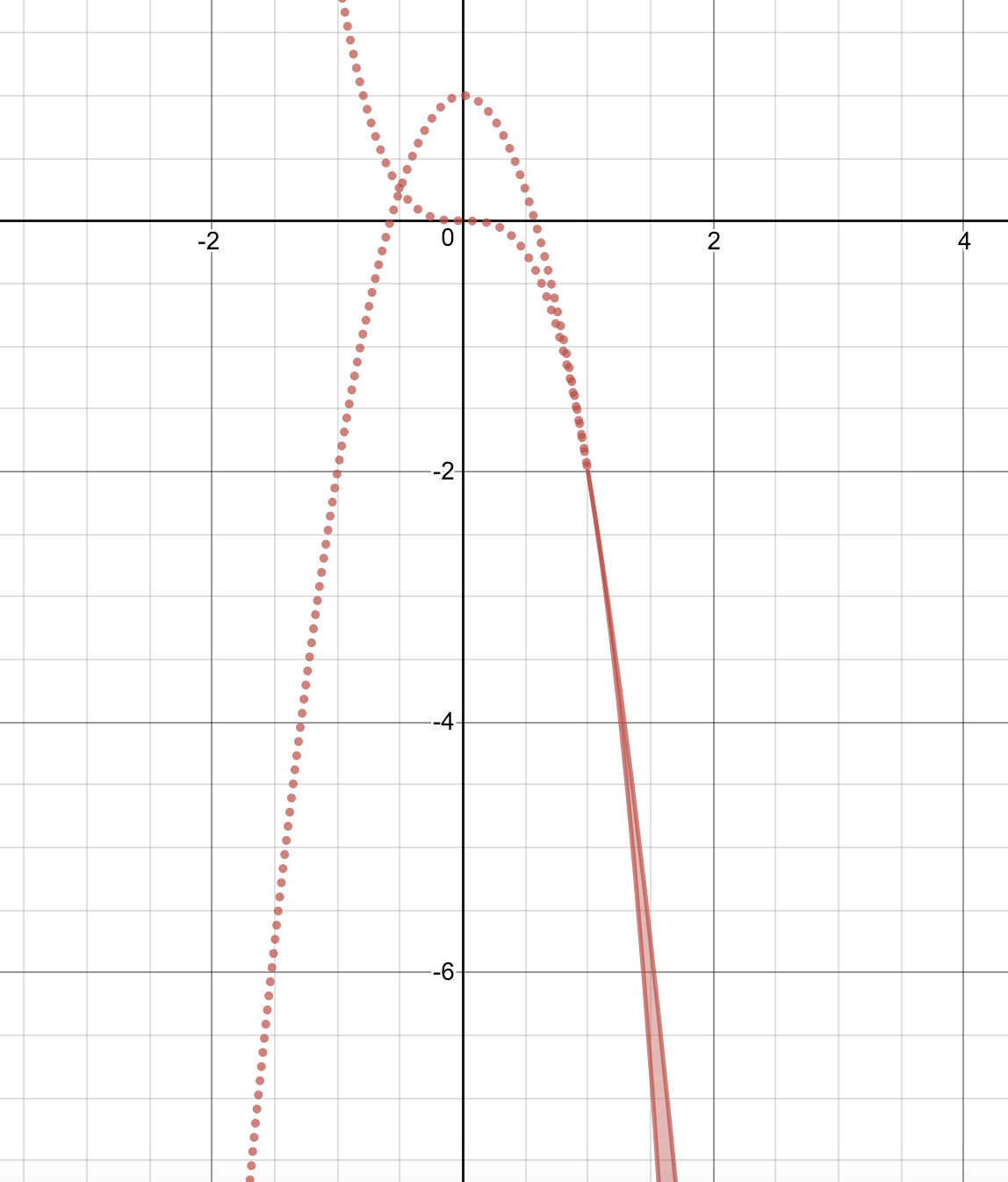
$y=-2x^3$と$y=1-3x^2$は$x=1$で接していることに注意しましょう。
第五問
第五問は以下のような問題でした。

第五問の難易度分析
複素数平面における軌跡の問題です。(1)は易しいものの、どのような誘導になっているのかが少し見抜きにくく、全体としての難易度は標準的でしょう。複素数平面上で図形の位置関係が与えられたときに、それを数式で表す手段を覚えているか、そして、逆に数式で与えられた条件がどのような図形的関係を表すかを覚えているかが鍵になったでしょう。
第五問(1)を解く上での考え方・ポイント
まずは、与えられた条件を数式として立てましょう!
図を描いてみると、点$\mathrm{Q}(u)$が満たすべき関係は、
1.$\mathrm{OP}$と$\mathrm{AQ}$が平行
2.$\mathrm{PA}=\mathrm{PQ}$
の2つだということがわかります。複素数平面における平行は、一方の実数倍がもう一方になるという式で表せますね。$|z|=1$であるので、$\bar{z}=\frac{1}{z}$が成り立つのも使って式変形をしていきます。
以下に解答例を示しておきます。
題意より、
1.$\mathrm{OP}$と$\mathrm{AQ}$が平行
2.$\mathrm{PA}=\mathrm{PQ}$
が成り立つので、$z\ne0$であることにも注意して、1つ目の条件は、
\[u-1=kz\]
をみたす実数$k(\ne 0)$が存在することと同値。
また、2つ目の条件は、
\[|z-1|=|z-u|\]
と表せるので、この式に$u=kz+1$を代入して、
\[\begin{align*}&|z-1|=|z-u|\\\Leftrightarrow&|z-1|=|(1-k)z-1|\\\Leftrightarrow&|z-1|^2=|(1-k)z-1|^2\\\Leftrightarrow&k^2-2k+kz+k\bar{z}=0\end{align*}\]
$k(\ne 0)$であるから、両辺$k$で割って、
\[k=2-z-\bar{z}\]
これを$u=kz+1$に代入して、$|z|=1$も考慮すると、
\[\boldsymbol{u=-z^2+2z}\]
$w=\frac{1}{1-u}$より、
\[w=\frac{1}{(z-1)^2}\]
であるから、$|z|=1$に注意して変形していくと、
\[\frac{\bar{w}}{w}=\frac{(z-1)^2}{(\bar{z}-1)^2}=\frac{z^2(z-1)^2}{(1-z)^2}=\boldsymbol{z^2}\]
さらに、
\[\begin{align*}\frac{|w+\bar{w}-1|}{|w|}=&\left|1+\frac{\bar{w}}{w}-\frac{1}{w}\right|\\=&|1+z^2-(z-1)^2|\\=&|2z|\\=&\boldsymbol{2}\end{align*}\]
計算していくだけなので、特に問題ないでしょう。
第五問(2)を解く上での考え方・ポイント
(2)は苦戦した受験生が多いのではないかと思います。(1)で、$\frac{|w+\bar{w}-1|}{|w|}=2$を求めたのが(2)にどのように活きてくるのかが見えにくいです。
ただ、複素数平面における軌跡を求めるときには、最終手段として$x+yi$とおいてしまう、というのがあるので、分からなければ単なる座標の問題として置き換えて進めてしまってもよいでしょう。
実際、$w=x+yi$とおけば、
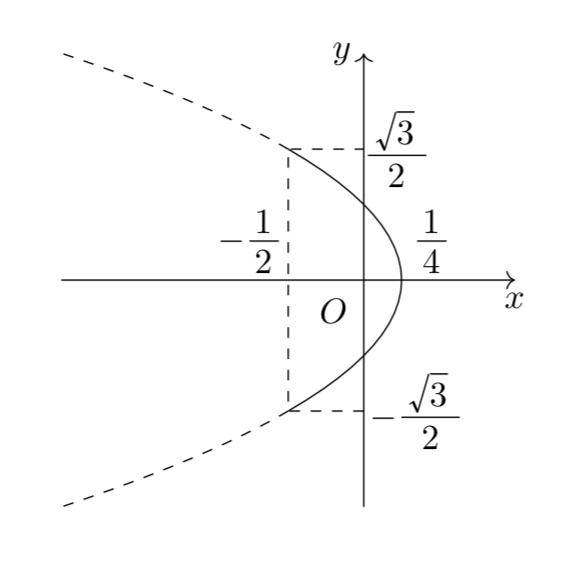
\[\frac{|2x-1|}{\sqrt{x^2+y^2}}=2\Leftrightarrow x=-y^2+\frac{1}{4}\]
となり、$w$の軌跡を簡単に求めることができます。つまり、横向きの放物線になるというわけですね。
これを上手く複素数のままで示すには、
\[\frac{|w+\bar{w}-1|}{|w|}=2\Leftrightarrow \left|\frac{w+\bar{w}}{2}-\frac{1}{2}\right|=|w|\]
と変形します。そうすると、$\frac{w+\bar{w}}{2}=Re(w)$であることから、$x=\frac{1}{2}$を準線、原点を焦点とする放物線を描くことがわかります。
今回は$x+yi$とおいてしまった方が答案が書きやすいでしょう。
また、$z$の実部が$\frac{1}{2}$以下であるという条件は、$|z|=1$を満たすことから$z=\cos \theta+i\sin \theta$とおいてしまえば、実部の条件を角度の条件に言い換えることができて、$w$の条件に繋げることができます。
以下、解答例を示しておきます。
$w=x+yi$とおくと、(1)より$\frac{|w+\bar{w}-1|}{|w|}=2$を満たすので、代入して、
\[\frac{|2x-1|}{\sqrt{x^2+y^2}}=2\]
両辺常に0以上なので、2乗して整理すると、
\[x=-y^2+\frac{1}{4}\]
また、$z=\cos \theta+i\sin \theta(0\leqq \theta< 2\pi)$とおくと、$z$の実部が$\frac{1}{2}$以下であるという条件は、$\frac{\pi}{3}\leqq\theta\leqq\frac{5}{3}\pi$と言い換えることができて、このとき、
\[\begin{align*}w=&\frac{1}{(z-1)^2}\\=&\frac{1}{(\cos \theta+i\sin \theta-1)^2}\\=&\frac{1}{(1-2\sin^2\frac{\theta}{2}+2i\sin\frac{\theta}{2}\cos\frac{\theta}{2}-1)^2}\\=&\frac{1}{\{2i\sin\frac{\theta}{2}(\cos \frac{\theta}{2}+i\sin \frac{\theta}{2})\}^2}\\=&\frac{-1}{4\sin^2\frac{\theta}{2}(\cos\theta+i\sin\theta)}\\=&\frac{-1}{4\sin^2\frac{\theta}{2}}\{\cos(-\theta)+i\sin(-\theta)\}\\=&\frac{1}{4\sin^2\frac{\theta}{2}}\{\cos(\pi-\theta)+i\sin(\pi-\theta)\}\end{align*}\]
となるので、$w$の偏角は$-\frac{2}{3}\pi\leqq\theta\leqq\frac{2}{3}\pi$を動くことになる。
以上より、求める軌跡を$xy$平面上に図示すると、以下の実線部。(ただし端点を含む)
第六問
第六問は以下のような問題でした。

第六問の難易度分析
立体図形の問題です。かなり丁寧に誘導がついているものの、立体や断面がどのような図形になるのかイメージがしにくく、解くのに時間がかかった受験生が多いのではないかと思われます。。よって、難易度としてはやや難くらいだと思われます。
とにかく、立体図形の問題の鉄則である
立体図形は適切な断面を取って考えよ
にしたがって、なるべく平面だけで考えるように意識することが大切でしょう。
第六問(1)を解く上での考え方・ポイント
$V_1,\,V_3$双方と共有点をもつという条件は、それぞれと共有点をもつ条件を「かつ」で結ぶだけでよいので、これは簡単でしょう。
図示するときには注意が必要です。$y=t$が$V_1$側に寄っているときと$V_3$側に寄っているときで形が変わるので気をつけましょう。
以下、解答例です。
$y=t$が$V_1,\,V_3$と共有点を持つための条件は、それぞれ、
\[-r\leqq t\leqq r,\,1-r\leqq t\leqq 1+r\]
であるから、$\frac{1}{2}<r<1$であることも考慮すると、求める条件は、
\[\boldsymbol{1-r\leqq t\leqq r}\]
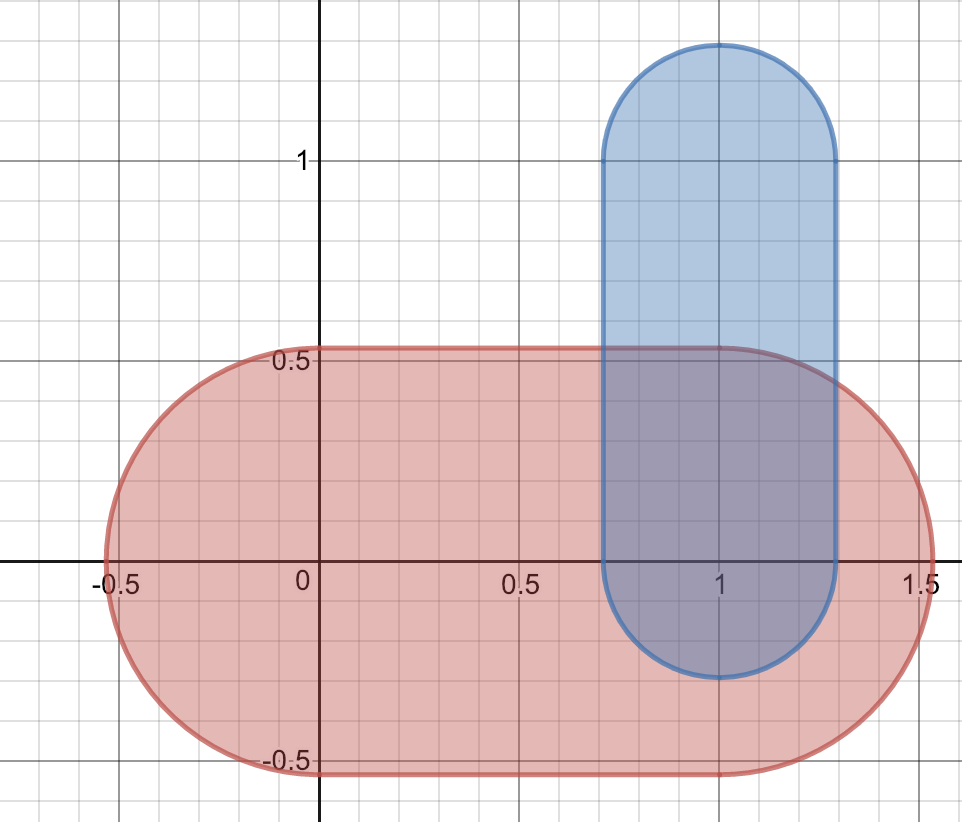
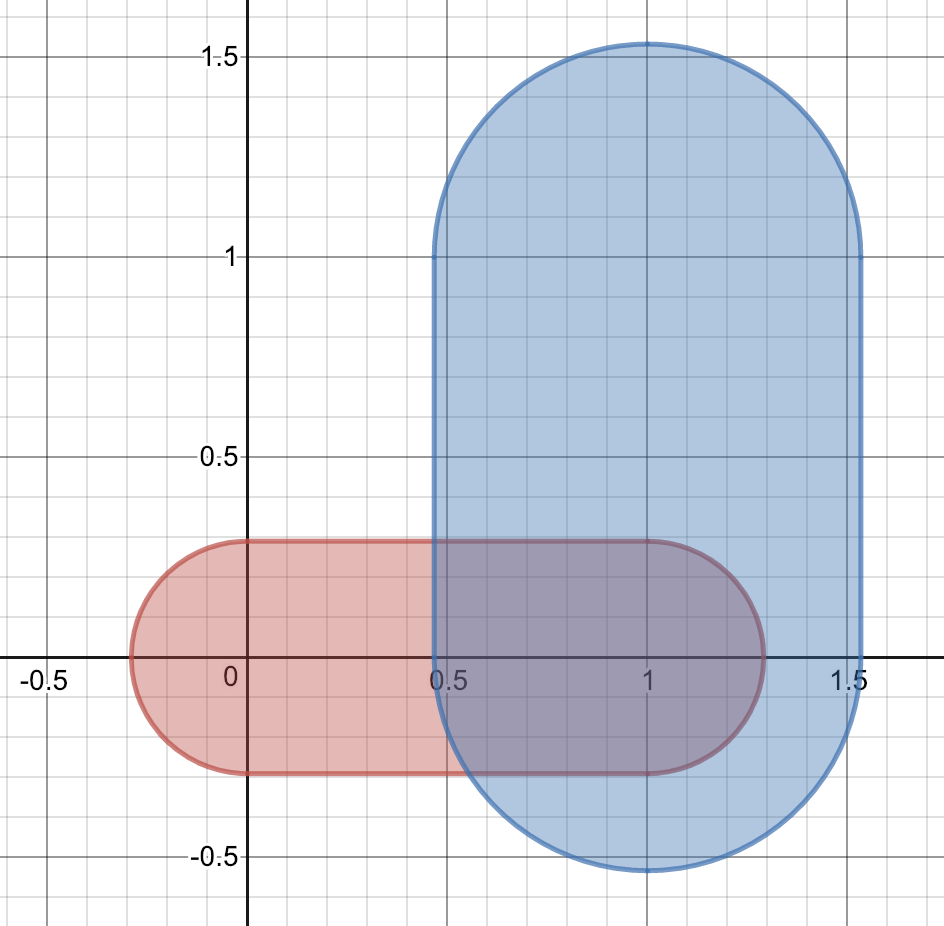
また、平面$y=t$と$V_1$の共通部分および、平面$y=t$と$V_3$の共通部分を図示すると以下のようになる。(境界はすべて含む)
(i)$1-r\leqq t\leqq\frac{1}{2}$のとき、
(ii)$\frac{1}{2}\leqq t\leqq r$のとき、
第六問(2)を解く上での考え方・ポイント
(1)ができていれば、$V_1$と$V_3$の共通部分の中で、最も$(x,\,z)=(1,\,0)$から最も遠い点が$V_2$の断面である円の内部にあればいいとすぐに分かると思います。
点$(x,\,z)=(1,\,0)$から最も遠い点は、$x=1-\sqrt{r^2-(1-t)^2}$と$z=\sqrt{r^2-t^2}$との共有点なので、その点に着目して議論を進めていきましょう。
また、(1)で求めた$1-r\leqq t\leqq r$の範囲においては$V_2$の断面が常に半径$r$の円であることにも注意しましょう。
(1)で求めた$1-r\leqq t\leqq r$の範囲においては、$y=t$上での$V_2$の断面は
\[(x-1)^2+z^2\leqq r^2\]
となる。(1)の図において、点$(x,\,z)=(1,\,0)$から最も遠い点は、$x=1-\sqrt{r^2-(t-1)^2}$と$z=\sqrt{r^2-t^2}$の共通点なので、求める条件は、
\[\begin{align*} &r^2-(t-1)^2+r^2-t^2\leqq r^2\\\Leftrightarrow &r^2\leqq 2\left(t-\frac{1}{2}\right)^2+\frac{1}{2}\end{align*}\]
が$1-r\leqq t\leqq r$をみたす$t$に対して常に成り立つことである。この範囲において、$2\left(t-\frac{1}{2}\right)^2+\frac{1}{2}$の最小値は$\frac{1}{2}$であるから、$\frac{1}{2}<r<1$であることも合わせて、求める条件は、
\[\boldsymbol{\frac{1}{2}<r\leqq \frac{1}{\sqrt{2}}}\]
第六問(3)を解く上での考え方・ポイント
3つの立体を重ねてできる体積について考える問題です。ベン図を考えてあげれば、簡単に解けます。
3つの立体$V_1,\,V_2,\,V_3$を重ねてできる立体の体積は、
\[(V_1の体積)+(V_2の体積)+(V_3の体積)\]
から、
を除いて、最後に、
\[(V_1,\, V_2,\,V_3の共通部分の体積)\]
を足すことによって計算できます。(2)の条件を満たすというのは、$(V_1,\, V_2,\,V_3の共通部分の体積)$が$(V_3,\, V_1共通部分の体積)$に等しいことを意味しているので、$S,\,T$だけで体積を表すことができます。
$V$の体積は、
によって求めることができて、
\[(V_1の体積)=(V_2の体積)=(V_3の体積)=S\]
\[\begin{align*}&(V_1,\, V_2の共通部分の体積)\\=&(V_2,\, V_3の共通部分の体積)\\=&T\end{align*}\]
が成り立ち、また、(2)の条件を満たすとき、
が成り立つので、$V$の体積は、
\[\boldsymbol{3T-2S}\]
第六問(4)を解く上での考え方・ポイント
(3)まで解けたら、$T,\,S$の値は簡単に求められますね!解答例だけを簡単に示しておきます。
$t$は、半径$1$の円を底面とする高さ$1$の直円柱の体積と、半径$1$の球の体積の和であるから、
\[S=\pi+\frac{4}{3}\pi\]
また、$V_1,\,V_2$の共通部分について、$z=p(-r\leqq p\leqq r)$での切り口は以下のようになる。
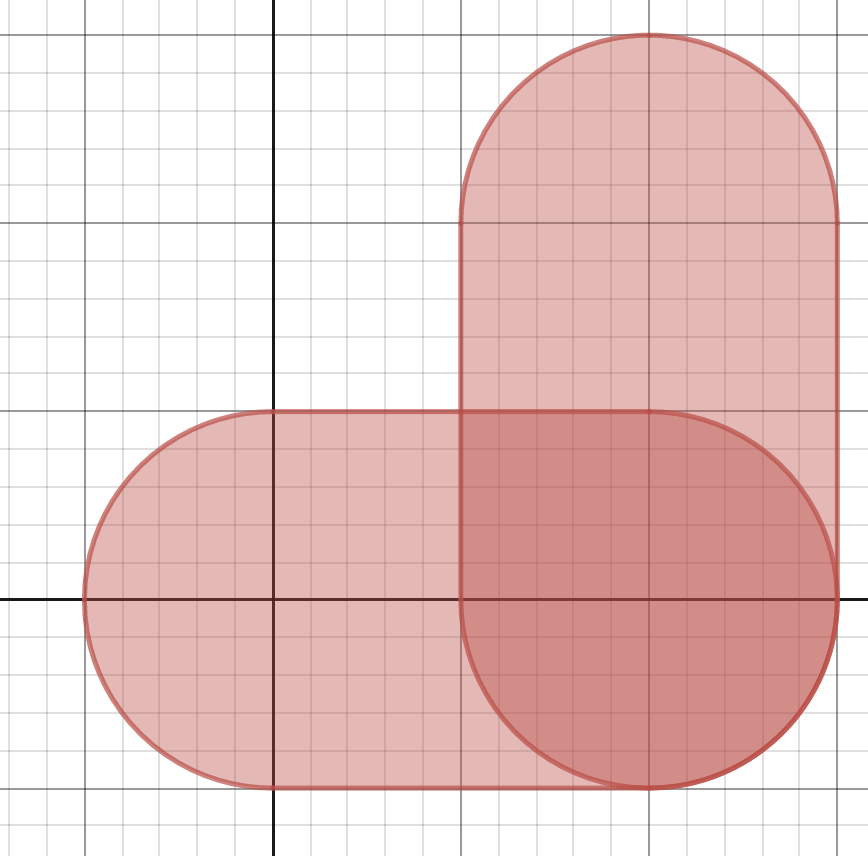
半径$\sqrt{r^2-p^2}$の四分円3つ分と、一辺$\sqrt{r^2-p^2}$の正方形1つ分の面積であるから、
\[T=\int_{-r}^{r}\left(\frac{3\pi}{4}+1\right)(r^2-p^2)dp=\left(\pi+\frac{4}{3}\right)r^3\]
したがって、(3)より、求める体積は、
\[3S-2T=\boldsymbol{3\pi r^2+\left(2\pi-\frac{8}{3}\right)r^3}\]
まとめ
全体として易しい問題が多いですが、第6問などは時間がかかり、満点を取るのはなかなか難しいでしょう。また、複素数平面の問題では、軌跡や動く範囲などを求めるのに苦戦した受験生が多いのではないかと思います。
第一問〜第四問までをしっかり取り切れたかどうかが勝負の分かれ目になったかと思います。
理三志望であれば、第五問、第六問以外は完答して90〜100点程度を狙いたい内容です。理一・理二志望であれば、それ以外の一問を落として70〜80点程度に収めたい内容です。
近年の東京大学の入試問題は数学が易しくなってきている傾向があるので、解けなかった問題がある人は反省してよく復習するべきだと思います。






