この記事を読むとわかること
・定数分離とはどういう手法か
・定数分離の使い方
・定数分離が使える条件
・定数分離が有効なときはいつか
・定数分離を用いる応用問題3つ
定数分離とは?
文字定数を含む項と含まない項に分けること
定数分離とは、方程式や不等式において文字定数を含む項と含まない項に分ける操作のことです。
例えば、
\[x^2-ax+1=0\]
という方程式に対して、
\[x^2+1=ax\]
というように、文字定数$a$を含む項と含まない項に分ける操作はまさに定数分離です。
定数分離したあとはグラフで考える
文字定数を含む項と含まない項に分けるのは、方程式の解を$y=(左辺)$、$y=(右辺)$という2つのグラフの交点の$x$座標として捉えたときに、2つのグラフがシンプルになるからです。
先程の例で言えば、$a$が変化するときに$y=x^2-ax+1$のグラフを考えるのは、放物線が動いてしまうので難しくなりますが、定数分離したあとでは、$y=x^2+1$と$y=ax$という2つのグラフになるので、動くものが直線になって非常に考えやすくなります。
定数分離したあとはグラフで考える!
定数分離するのはグラフで考えるために必要な処理の1つなんだな、という意識を持っておくとよいでしょう。
文字定数分離やパラメータ分離とも呼ばれる
定数分離は、「文字定数分離」や「パラメータ分離」と呼ばれることも多いので、インターネットで検索するときにはこれらの単語での検索も行うとよいでしょう。
この記事の中では、定数分離という呼び方で統一しておきます。
定数分離の使い方
先ほども述べた通り、文字定数を分離するのはグラフで考えるための最初の一歩でしかありません。以下の4つの手順を覚えて初めて定数分離の使い方をマスターしたと言えるでしょう!
定数分離の使い方!
1.文字定数を含む項と含まない項に分ける
2.$y=(左辺)$、$y=(右辺)$の2つのグラフを描く
3.グラフが接する時、端点を通るときを求める
4.グラフを見て条件を満たす時を求める
例題として以下の問題を考えながら、定数分離の使い方について学んでいきましょう。
$x$の2次方程式
\[x^2+2ax-a+1=0\]
が$-1<x<3$の範囲にただ1つの実数解を持つための実数$a$の条件を求めよ。(重解の場合もただ1つの実数解の場合に含む)
文字定数を含む項と含まない項に分ける
まずは、文字定数である$a$を含む項と含まない項に分けましょう。上の例題であれば、
\[x^2+2ax-a+1=0\Leftrightarrow 2ax-a=-x^2-1\]
というように分けられますね!
y=(左辺)、y=(右辺)の2つのグラフを描く
定数分離ができたら、$y=(左辺)$、$y=(右辺)$のグラフを描きます。このときに注意したいのは、文字定数を含んでいる方はグラフの形が定まっていないということです。
上の例題で言えば、$y=-x^2-1$のグラフを描くことはできても、$y=2ax-a$のグラフを描くのは$a$の値によってグラフが変化して描きづらいです。しかし、
\[y=2ax-a\Leftrightarrow y=2a\left(x-\frac{1}{2}\right)\]
と変形することによって、直線が$a$の値によらず常に$(\frac{1}{2},\,0)$という点を通ることに気づきます。
文字定数を含む直線は、常に通る点に着目する!
このポイントを覚えておきましょう。
グラフが接するとき、端点を通るときを求める
実数解の個数について考えていくためには、グラフの共有点の個数が変化するときがいつなのかを知る必要がありますよね。「2つのグラフの共有点の個数が変化するのっていつだろう…?」と考えてみると、それは、2つのグラフが接するときと端点を通るときです。
上の例題で言えば、接する時は以下の2つですね。
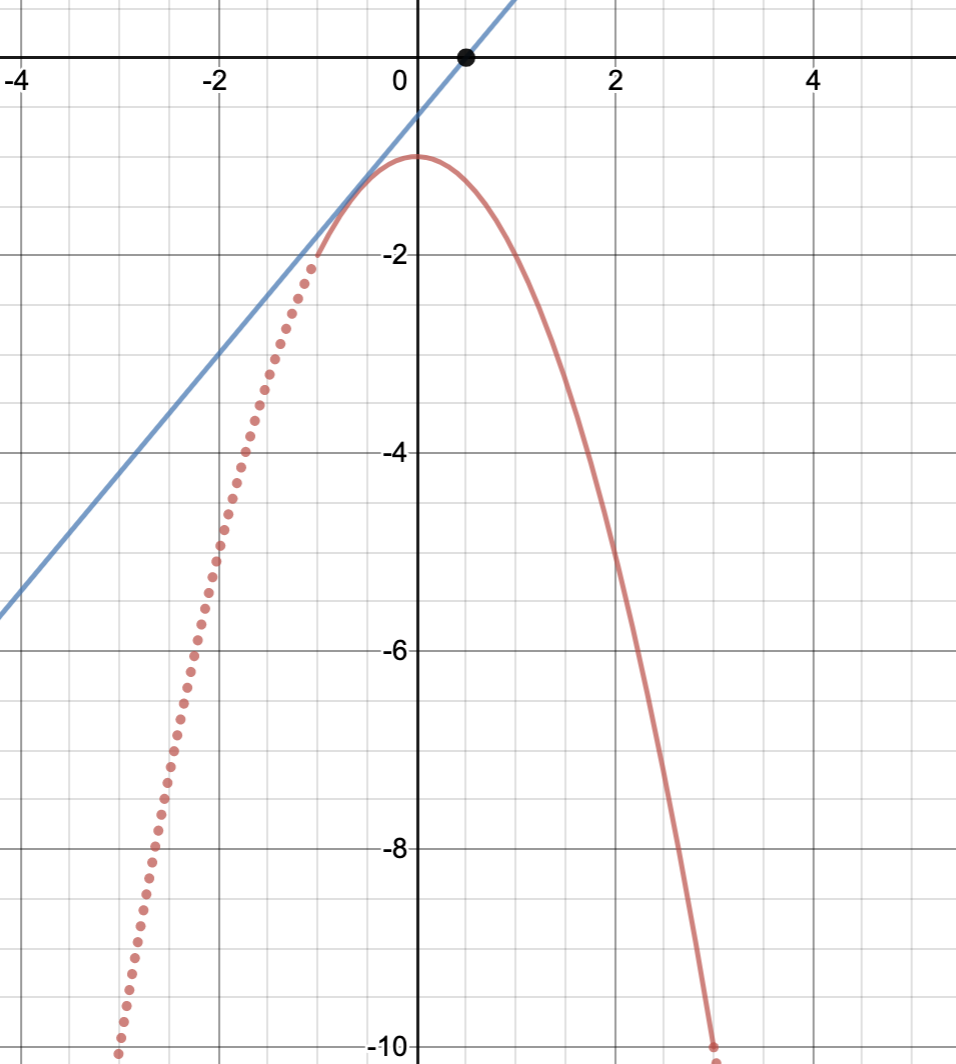
接する時の$a$の値を求めましょう。接する時は方程式が重解を持つ時と等しいので、判別式を考えればOKですね!$x^2+2ax-a+1=0$の判別式を$D$とすると、
\[\frac{D}{4}=0\Leftrightarrow a^2+a-1=0\Leftrightarrow a=\frac{-1\pm\sqrt{5}}{2}\]
となるので、これが接する時の$a$の値となります。このときに気をつけたいのが接する時の$x$座標が本当に与えられた範囲の中にあるかということです。$D=0$を考えていても、重解が$-1<x<3$の範囲の中に入っていなかったら、グラフを使って考察するときに何も意味を持たないですよね。
重解が与えられた範囲に入っているかどうか必ずチェック!
重解は必ず軸の位置なので、今回の例題で言えば、重解を持つ場合には$x=-a$が重解になりますよね。$a=\frac{-1\pm\sqrt{5}}{2}$のどちらの場合も、
\[-1<\frac{1+\sqrt{5}}{2}<3\]
\[-1<\frac{1-\sqrt{5}}{2}<3\]
となるので問題なさそうです!
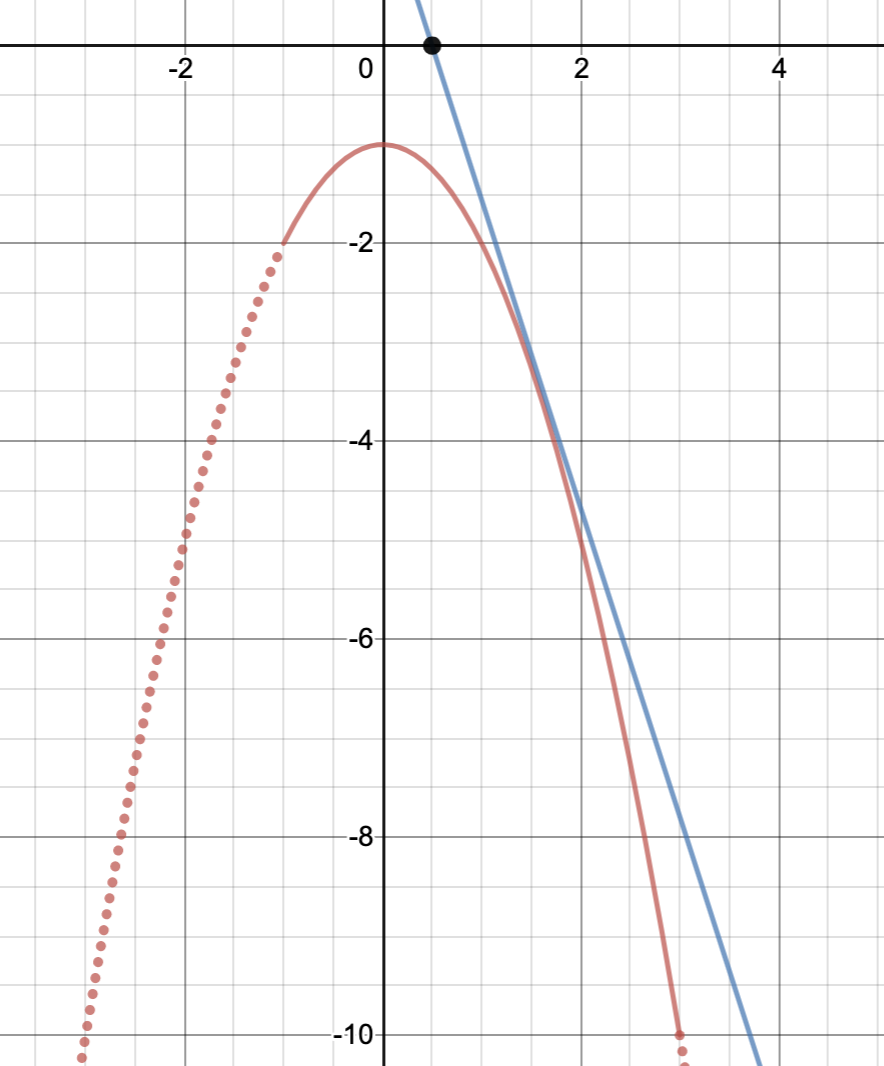
また、端点を通るときもグラフの共有点の個数が変化するときですよね。例題で言えば、下図のように区間の端である$(-1,\,-2),\,(3,\,-10)$を通るときの$a$の値を求めなければなりません。
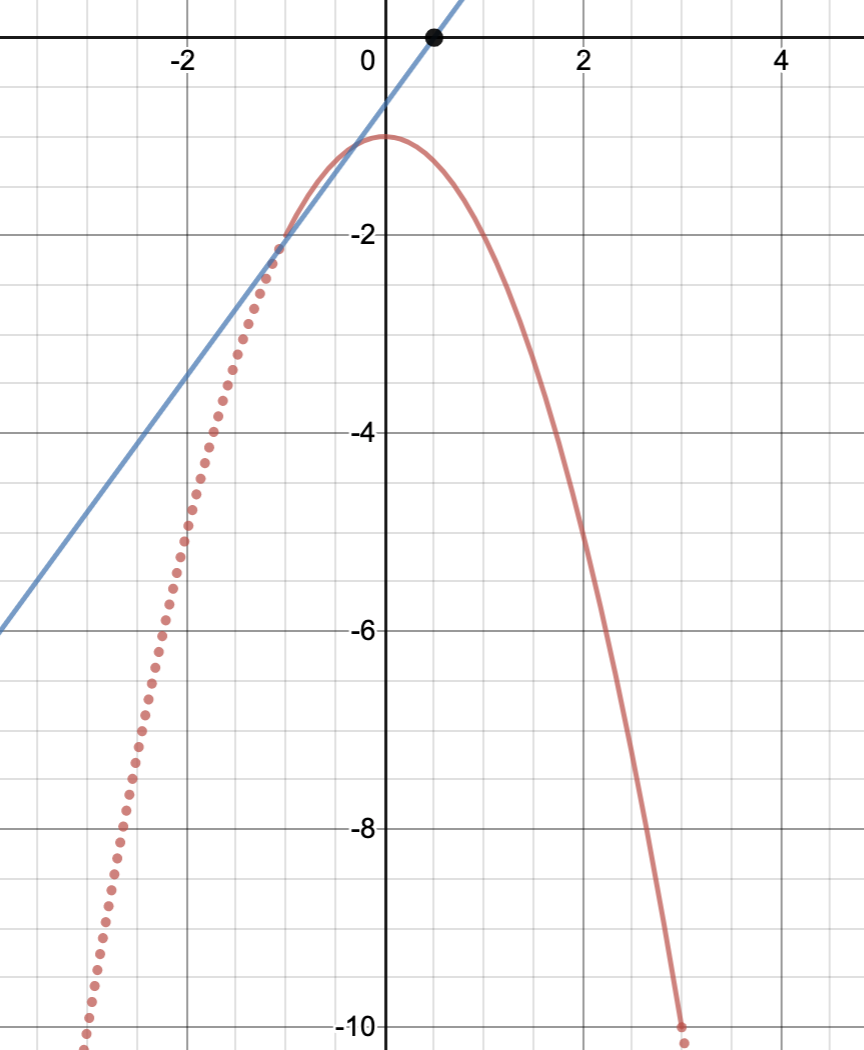
このときの$a$の値はそれぞれ座標の値を代入するだけで求められますね!
\[2=2a(-1)-a\Leftrightarrow a=\frac{2}{3}\]
\[-10=2a\cdot 3-a\Leftrightarrow a=-2\]
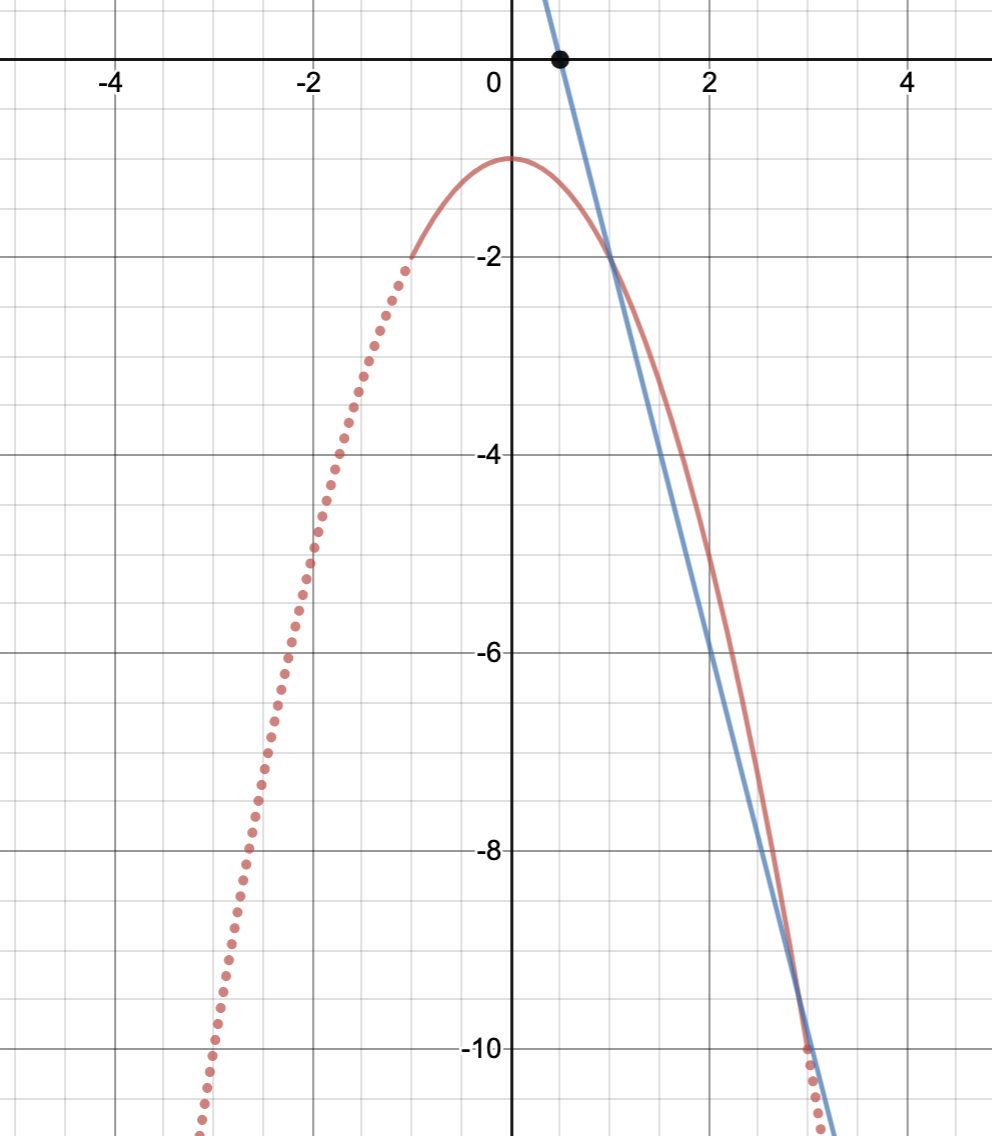
グラフを見て条件を満たすときを考える
共有点の個数が変化するときが分かったので、あとはグラフを見ながら条件を満たすときを考えていくだけです!
共有点がちょうど1つになるのは、もちろん、接するときも考えられますが、下図のように、端点を通るときよりも傾きが急になっているときもありますよね。
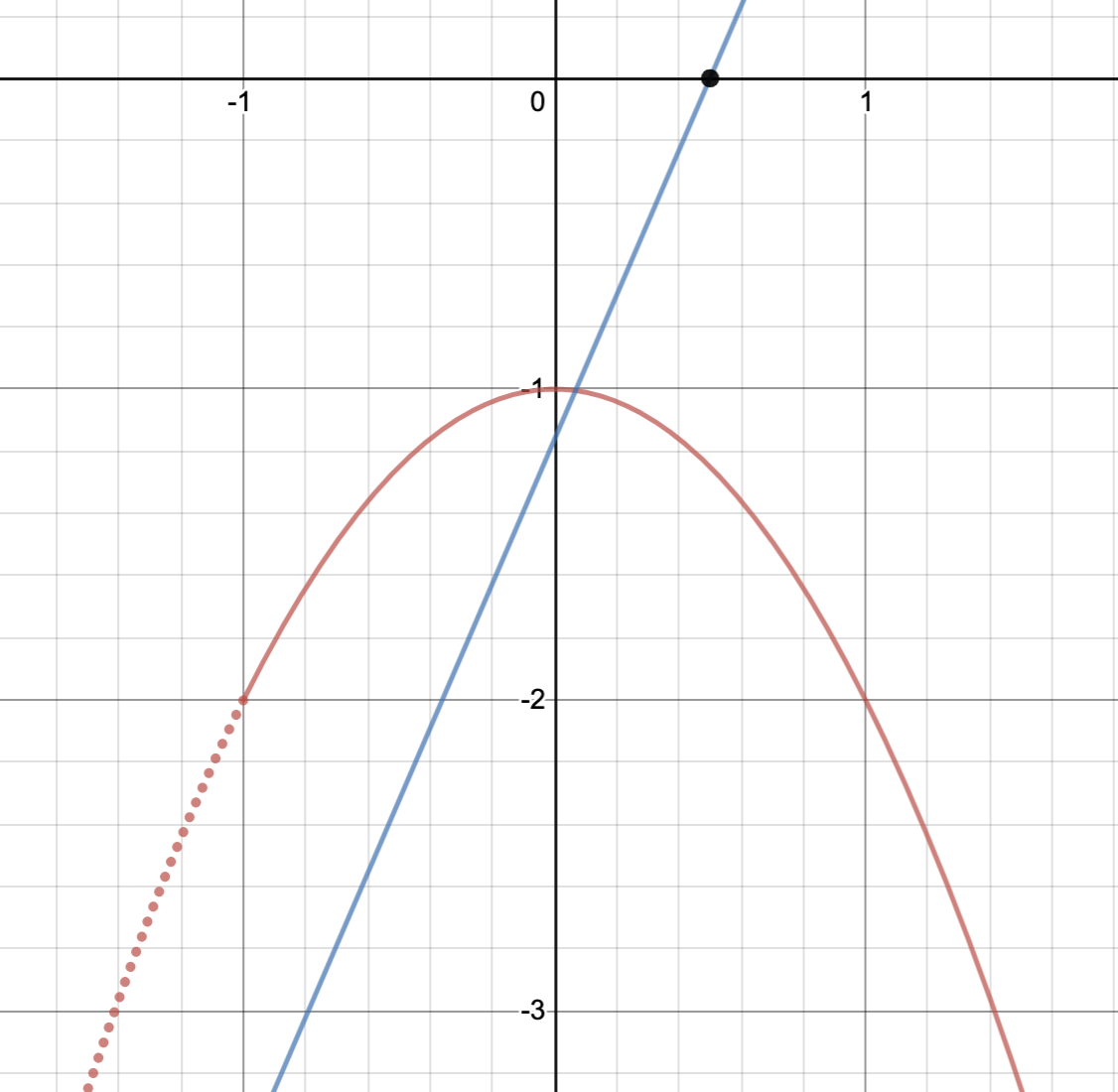
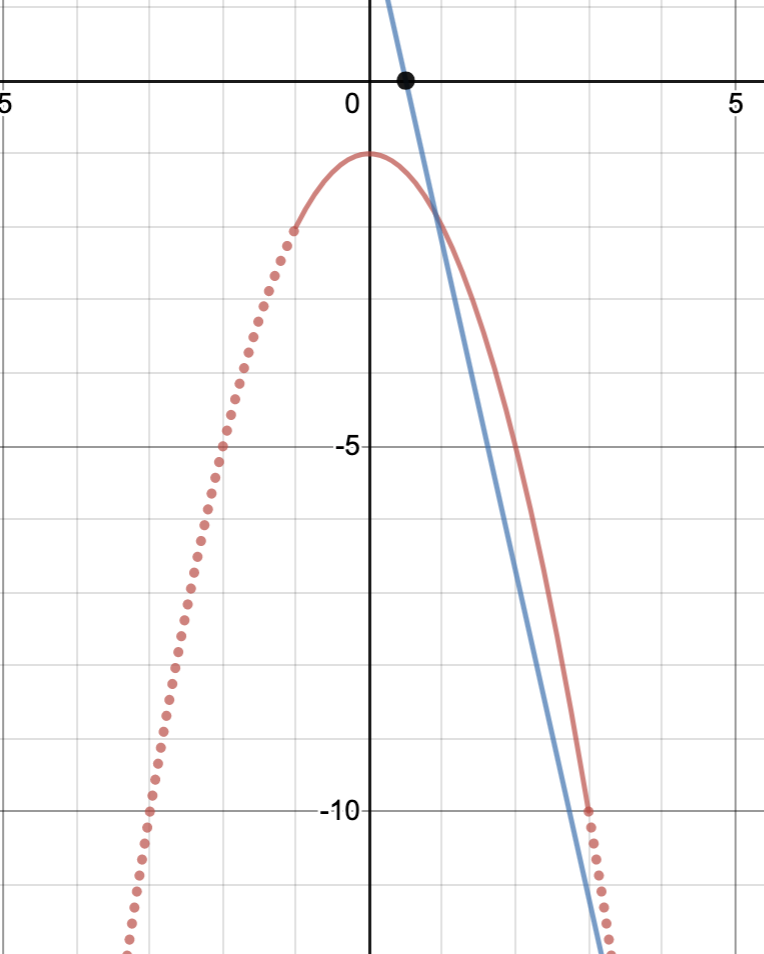
したがって、求める答えは、
\[\boldsymbol{a\leqq-2,\,a=\frac{-1\pm\sqrt{5}}{2},\,\frac{2}{3}\leqq a}\]
となります。今回の問題では与えられた区間が$-1<x<3$となっていうので、ちょうど端点を通っているときも条件を満たしていることに注意しましょう。
定数分離が使える条件は?
定数分離という手法が使える条件って何なんでしょうか。
「文字定数が入ってたらいつでも定数分離って使えるんじゃないの…?」と思いたくなりますが、実はそうでもありません。
文字定数が含まれてる部分が1次以下の式なら使える!
前述の通り、定数分離という手法がそもそもグラフを使って考えるためにあるということを考えると、文字定数が含まれる部分が図示できない場合、定数分離をやってもしょうがないですよね。
2次以上の関数に文字定数が含まれていると、そのグラフの動きを考えるのはかなり難しいですが、直線が動くのは簡単です。よって、文字定数が含まれている部分が1次以下なら定数分離は使えるということになります。
定数分離が使える条件は、文字定数が含まれている式が1次以下であること!
文字定数について1次であることも大事
定数分離は、そもそも文字定数自体が2次以上になっていると使えないケースが多いです。例えば、
\[x^2-a^2x+a=0\]
という方程式を定数分離によって考えようとすると、
\[x^2=a^2x-a\]
と分離することになりますが、$y=a^2x-a$という直線は$a$によらず通る定点が存在しないのでグラフの動きを考えるのは難しそうですよね。結局、文字定数について1次であることも、定数分離が使えるための条件と言って良いでしょう。
文字定数について1次であることも定数分離が使えるための条件!
以上の2つが定数分離が使える条件になります。
定数分離が有効なのはいつ?
定数分離の使える条件をみたしていても、わざわざそれを使わなくてもよいケースというのは多々あります。定数分離という手法が有効なのはどのようなときでしょうか?
文字定数が含まれていない部分が特殊な関数のとき
文字定数が含まれていない部分が特殊な関数のときは、定数分離によって非常に見通しがよくなります。この場合、定数分離をすると、「複雑だが動かないグラフ」と「シンプルな動くグラフ」の2つのグラフの交点を考えることになり、愚直に方程式の解について考えるよりもはるかに考えやすいです。
「特殊な関数」と言ったものとしては、無理関数やガウスの関数、双曲線や絶対値を含む関数など、様々なものが考えられます。記事の後半では定数分離を用いることによって解ける応用問題をたくさん紹介しているので、それを解くことによって、”定数分離のありがたみ“を感じられるでしょう。
2次方程式なら解の配置で十分
市販の参考書や問題集では定数分離を用いる問題の例として2次方程式のケースばかりを挙げがちですが、これは定数分離を学ぶ例としては不適切だと思います。
なぜなら、2次方程式の解の個数や範囲について考えるには解の配置の考え方を使ってしまえば良いからです。先ほど定数分離の使い方を学ぶために挙げた例題もよく考えてみれば、ただの解の配置問題ですよね。
以下の記事に同じ問題を解の配置の考え方によって解いているので、興味がある方は読んでみてください。
定数分離の応用問題3選
定数分離の使い方と使える条件、有効なときを学んだので、あとは問題をたくさん解きましょう!ここでは、定数分離の入試問題や応用問題を3つ紹介したいと思います。
問題1
$a$を実数の定数とする。$x$の方程式
\[\sqrt{x-1}-ax=0\]
の実数解の個数を求めよ。
解答
\[\sqrt{x-1}-ax=0\Leftrightarrow \sqrt{x-1}=ax\]この方程式の解は、$y=\sqrt{x-1}$と$y=ax$の共有点の$x$座標に等しいので、2つのグラフの共有点の個数について調べればよい。
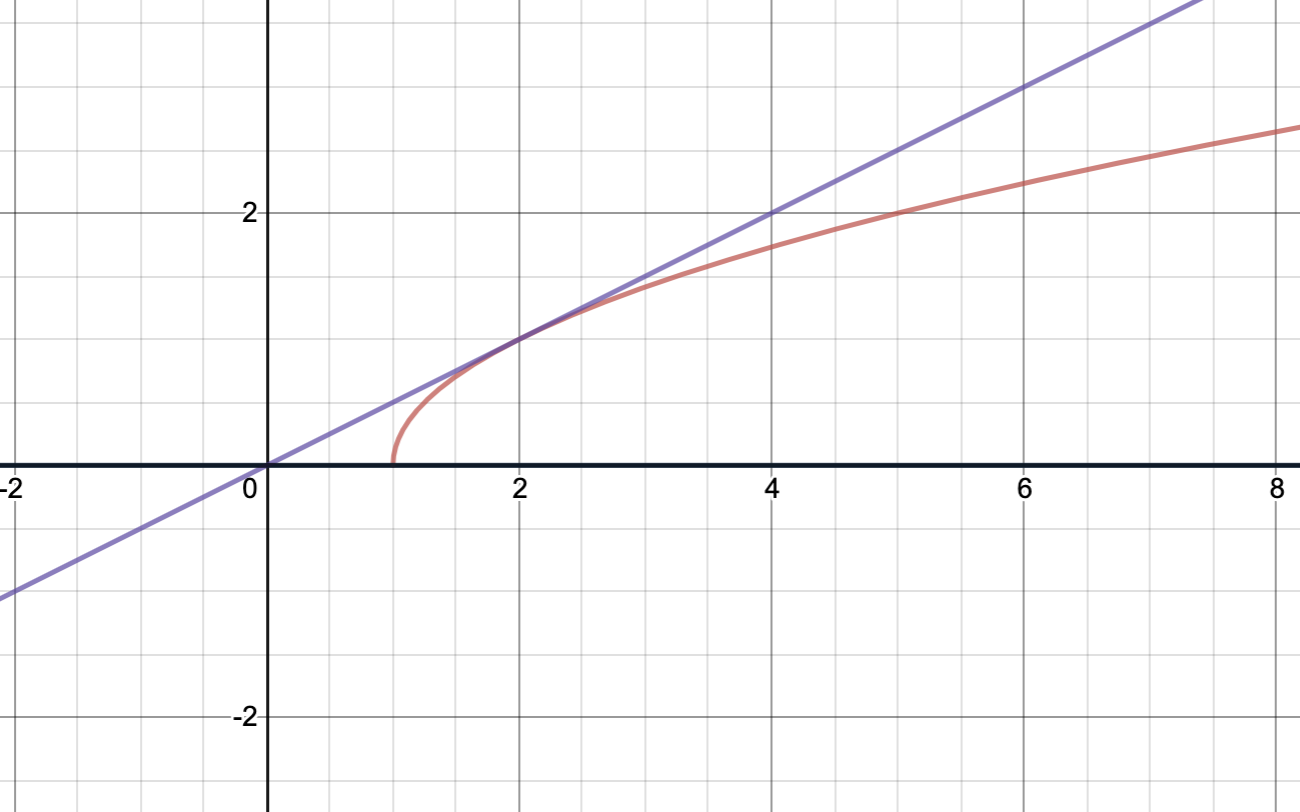
(i)$y=\sqrt{x-1}$と$y=ax$が接するとき、
$\sqrt{x-1}=ax$が重解を持てばよい。よって、
\[\begin{align*}&\sqrt{x-1}=ax\\\Leftrightarrow & x-1=a^2x^2 かつ ax\geqq 0\\\Leftrightarrow &a^2x^2-x+1=0 かつ ax\geqq 0\end{align*}\]
これが重解を持てばよい。$a=0$のときは重解を持ち得ないので、$a\ne 0$としてよく、このとき判別式を$D$とすれば、重解を持つときその重解は$x=\frac{1}{2a^2}$となることより、
\[\begin{align*}&D=0 かつ a\cdot \frac{1}{2a^2}\geqq 0\\\Leftrightarrow &1-4a^2=0 かつ a\geqq 0\\\Leftrightarrow &a=\frac{1}{2}\end{align*}\]
(ii)$y=ax$が点$(1,\,0)$を通るとき、$a=0$である。
以上(i)(ii)より、グラフから、求める実数解の個数は、
\[\left\{\begin{array}{l}\boldsymbol{a<0のとき0個}\\\boldsymbol{a=0のとき1個}\\\boldsymbol{0<a<\frac{1}{2}のとき2個}\\\boldsymbol{a=\frac{1}{2}のとき1個}\\\boldsymbol{a>\frac{1}{2}のとき0個}\end{array}\right.\]
解説
定数分離をすることによって、与えられた無理方程式の実数解の個数を無理関数と直線の共有点の個数と捉え直して解いています。もともとは方程式の問題だったわけですから、グラフで考えることを宣言する必要がありますよね。
そこで、「この方程式の解は、$y=\sqrt{x-1}$と$y=ax$の共有点の$x$座標に等しいので、2つのグラフの共有点の個数について調べればよい。」という記述を書いていることに注意しましょう。
また、両辺を2乗するときには同値性を保つために、$ax\geqq 0$という条件がつくことにも気をつけてください。
問題2
$a$を実数の定数とする。$x$の方程式
\[\sqrt{1-x^2}-ax-2a=0\]
の実数解の個数を求めよ。
解答
\[\sqrt{1-x^2}-ax-2=0\Leftrightarrow \sqrt{1-x^2}=a(x+2)\]この方程式の解は、$y=\sqrt{1-x^2}$と$y=a(x+2)$の共有点の$x$座標に等しいので、2つのグラフの共有点の個数について調べればよい。
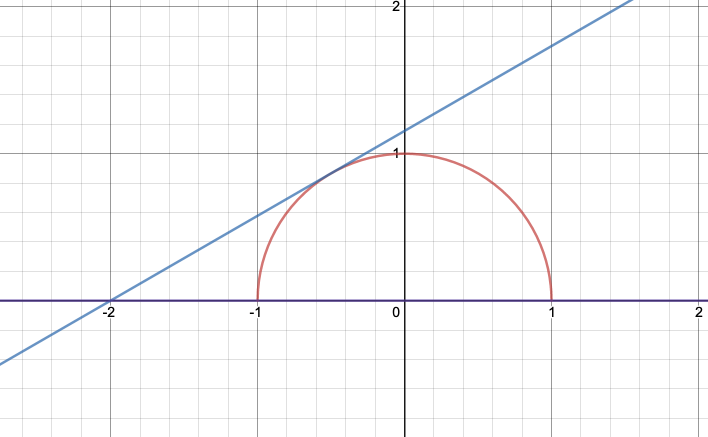
$y=\sqrt{1-x^2}$は上図のような半円を表すので、これと直線$y=a(x+2)$が接するのは、点と直線の距離の公式より、
\[\begin{align*}&\frac{|-2a|}{\sqrt{a^2+1}}=1\\\Leftrightarrow& |-2a|=\sqrt{a^2+1}\\\Leftrightarrow& 4a^2=a^2+1\\\Leftrightarrow &a=\pm\frac{1}{\sqrt{3}}\end{align*}\]
これと図より、接する時の$a$の値は、
\[a=\frac{1}{\sqrt{3}}\]
また、点$(-1,\,0),\,(1,\,0)$を通るときはどちらも$a=0$となるので、上のグラフより、求める解の個数は、
\[\left\{\begin{array}{l}\boldsymbol{a<0のとき0個}\\\boldsymbol{0\leqq a<\frac{1}{\sqrt{3}}のとき2個}\\\boldsymbol{a=\frac{1}{\sqrt{3}}のとき1個}\\\boldsymbol{a>\frac{1}{\sqrt{3}}のとき0個}\end{array}\right.\]
解説
問題1と式の形は似ていますが、今回はグラフが半円の形になることに注意しましょう。円の場合は接する条件を考えるときに点と直線の距離の公式を使えばいいですね!原点(円の中心)と直線までの距離が1(円の半径)に等しい条件を考えています。
また、両辺を2乗するときには同値性に気をつけなければなりませんが、$|-2a|=\sqrt{a^2+1}$は両辺常に0以上になっているので、2乗した式は同値な式になっていることに注意しましょう。
問題3
実数$x$に対して、$x$を越えない最大の整数を$[x]$で表す。このとき、$2\leqq x< 4$の範囲において、$x$の方程式
\[[x]-ax=0\]
は相異なる実数解をいくつ持つか。ただし、$a$は実数の定数とする。
解答
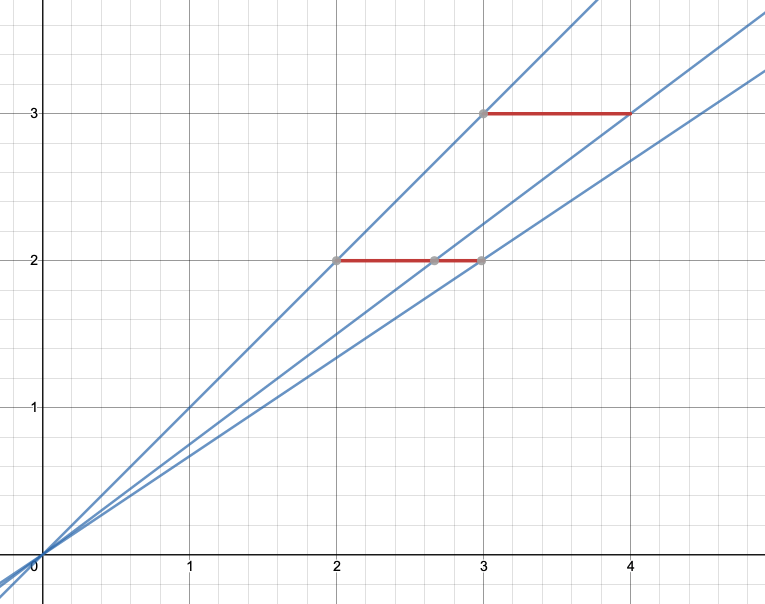
(i)$y=ax$が点$(3,\,2)$を通るとき、
\[2=3a\Leftrightarrow a=\frac{2}{3}\](ii)$y=ax$が点$(4,\,3)$を通るとき、
\[3=4a\Leftrightarrow a=\frac{3}{4}\](ii)$y=ax$が点$(2,\,2),\,(3,\,3)$を通るとき、
\[a=1\]
したがって、上のグラフより、求める実数解の個数は、
\[\left\{\begin{array}{l}\boldsymbol{a\leqq \frac{2}{3}のとき0個}\\\boldsymbol{\frac{2}{3}< a\leqq \frac{3}{4}のとき1個}\\\boldsymbol{\frac{3}{4}<a\leqq 1のとき2個}\\\boldsymbol{a>1のとき0個}\end{array}\right.\]
解説
ガウス記号が絡んだ問題です。ガウス記号の定義を確認しておきましょう!
ガウス記号の定義
実数$x$に対して、
\[k\leqq x<k+1\]
を満たす整数$k$を$[x]$と表す。
よって、$y=[x]$のグラフを描くと階段状のグラフになることが分かると思います。$2\leqq x<4$の区間であれば、
\[[x]=\left\{\begin{array}{l}2(2\leqq x<3のとき)\\3(3\leqq x<4のとき)\end{array}\right.\]
となりますね。各線分の右端は含まれないので、$y=ax$が$(3,\,2)$や$(4,\,3)$を通っても実数解を持たないことに注意してくださいね。
まとめ
・定数分離とは、方程式や不等式で文字定数を含む項と含まない項に分ける操作のこと
・定数分離したあとは$y=(左辺)$、$y=(右辺)$のグラフを描いて、接する時や端点を通る時に注意して実数解について考える
・定数分離が使える条件は文字定数が含まれている部分が1次式で、かつ、文字定数について1次であること
・定数分離が有効になるのは、無理関数やガウス記号の関数などの特殊な関数のとき
・2次方程式なら解の配置で考えれば十分






