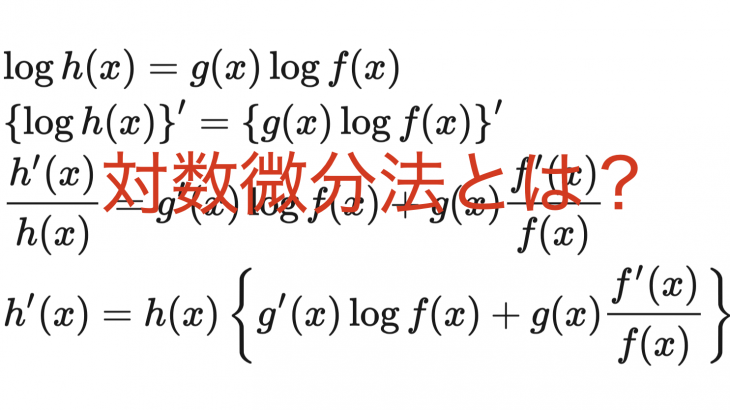この記事を読むとわかること
・媒介変数表示とは
・媒介変数表示されたグラフの描き方3通り
・それぞれのグラフの描き方を練習できる例題
媒介変数表示されたグラフの描き方は?
そもそも媒介変数表示とは
媒介変数表示とは、関数を$x,\,y$の2文字の方程式ではなく、新たな変数を用いて$x,\,y$をそれぞれ書き表すことによって定義する書き方のことを指します。
例えば、
\[\left\{\begin{array}{l}x=f(t)\\y=g(t)\end{array}\right.\]
というように、ある変数$t$の関数として$x,\,y$がそれぞれ書き表されているとき、この$t$のことを媒介変数(パラメータ)と呼びます。この記事では、媒介変数ではパラメータという呼び方で統一しておきます。
グラフの描き方には主に3通りある
媒介変数表示された曲線のグラフの描き方は主に3通りあります。
媒介変数表示された曲線のグラフの描き方
1.パラメータを消去する
2.パラメータで微分して増減表を描く
3.パラメータについてベクトルを整理する
1のやり方が一般的で、2のやり方が最も汎用性が高く、3のやり方は上手く使える時がたまにあるといった感じです。
これら3通りのやり方がどのようなものなのか、それぞれ例題付きで説明していきたいと思います!
パラメータを消去するやり方
一般的なパラメータを消去して関数を求め、グラフを描くやり方を見てみましょう!
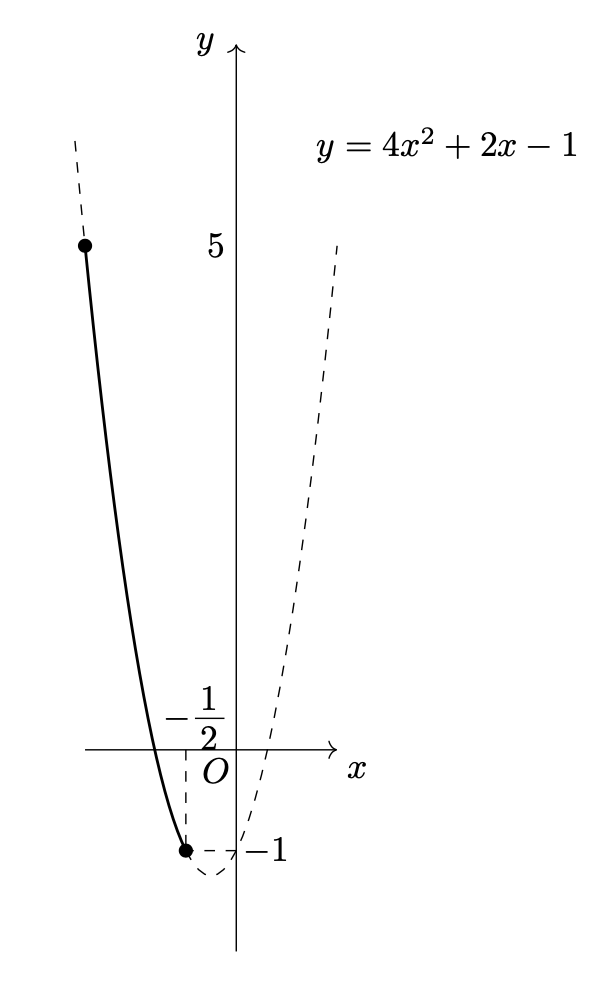
解答
\[x=\frac{1}{2}t-1\Leftrightarrow t=2(x+1)\]
であるから、$y=t^2-3t+1$と$-1\leqq t\leqq 1$に代入して、
\[\begin{align*}&\left\{\begin{array}{l}y=\{2(x+1)\}^2-3\{2(x+1)\}+1\\-1\leqq 2(x+1)\leqq 1\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}y=4x^2+2x-1\\-\frac{3}{2}\leqq x\leqq -\frac{1}{2}\end{array}\right.\end{align*}\]
したがって、点$\mathrm{P}(x,\,y)$が描く曲線は以下の太線部。(ただし黒丸を含む。)
解くときの注意点
パラメータを消去する解法は簡単ですが、パラメータを消去するときに$t$の動く範囲の条件にも代入する、という作業をやり忘れると正しい定義域が求まらないので注意しましょう。
また、この解法はパラメータを消去した結果、簡単に図示のできる関数になった場合には上手くいきますが、どのような関数なのかわからないときには、陰関数の微分を使って図示をすることになります。
そこでよく考えてみると、結局微分をするのであれば、媒介変数表示されているときに微分してしまえばいいんです。パラメータで微分する解法を以下で説明していきます。
パラメータで微分して増減表を描くやり方
パラメータ消去してもよくわからない関数が出てきてしまうときには、媒介変数表示されている状態でパラメータ微分をして増減表を描き、グラフを描きましょう!

解答
\[\left\{\begin{array}{l}x=\frac{\sqrt{3}}{2}t^2-\frac{1}{2}t\\y=\frac{1}{2}t^2+\frac{\sqrt{3}}{2}t\end{array}\right.\]
について、それぞれ$t$で微分すると、
\[\left\{\begin{array}{l}\frac{dx}{dt}=\sqrt{3}t-\frac{1}{2}\\\frac{dy}{dt}=t+\frac{\sqrt{3}}{2}\\\end{array}\right.\]
であるから、増減表は以下のようになる。
また、
\[\begin{align*}\frac{d^2y}{dx^2}=&\frac{dt}{dx}\cdot\frac{d}{dt}\frac{dy}{dx}\\=&\frac{-2}{\left(\sqrt{3}t-\frac{1}{2}\right)^3}\end{align*}\]
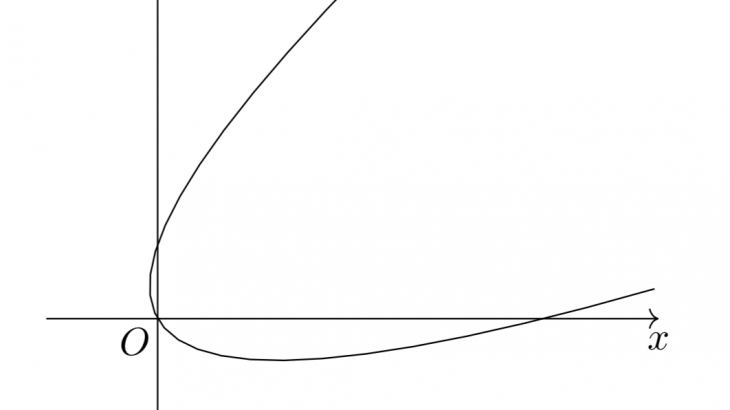
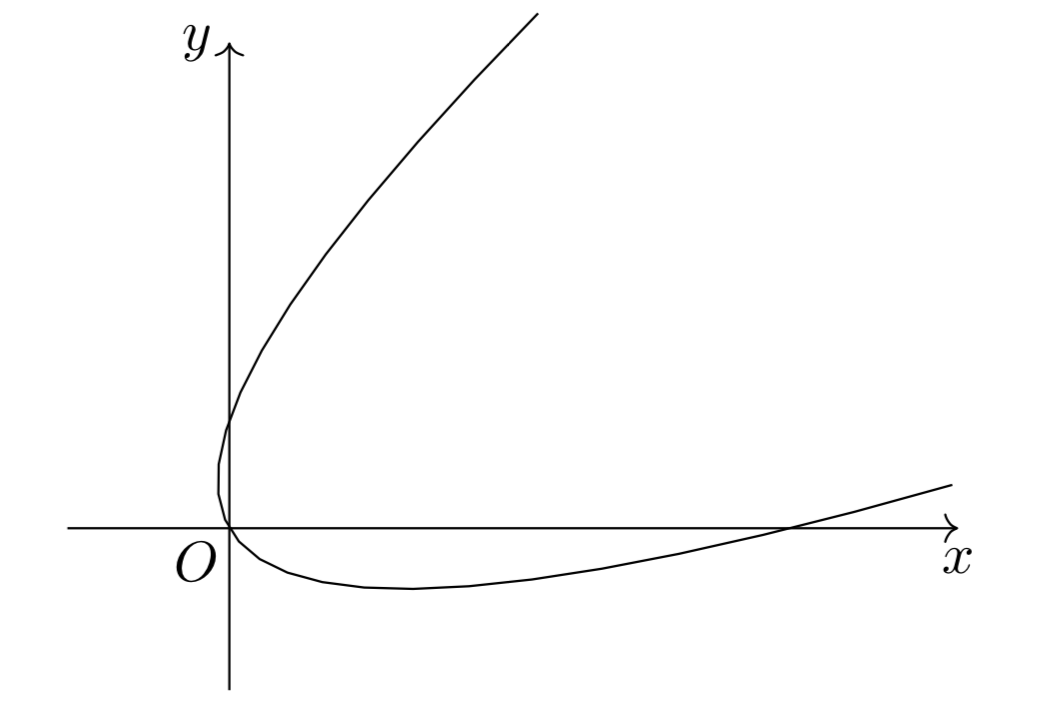
より、$t< \frac{\sqrt{3}}{6}$のとき下に凸、$\frac{\sqrt{3}}{6}<t$のとき上に凸になることも考慮すると、求めるグラフは以下のようになる。
解くときの注意点
今回の問題では、$t$を消去することによって得られる関数が、$x^2-2\sqrt{3}xy+3y^2-2\sqrt{3}x-2y=0$という簡単に図示できないものなので、こういうときにはパラメータの微分をすることによって、グラフの概形を図示することができます。
これは、ほとんどの場合に対して有効な解法であり、覚えておく価値は非常に高いです。
ただし、得られたグラフを見てみると、放物線のような形になっているものの、これが放物線と同じ形かどうかを判別することはこの解法ではできません。このように、あくまで概形を把握することができず、具体的にはどのような関数であるのかどうかを考えることができないことに注意しましょう。
実は、次に紹介するパラメータについてベクトルを整理するという作業を行うとこれが放物線を回転させたものだとわかります。
パラメータについてベクトルを整理するやり方
パラメータについてベクトルを整理をしてあげてから適切な変換を行ってあげることによって、関数がどのようなものなのか詳細に把握できる場合があります。先ほどと同じ例題をこの解き方でやってみましょう!
解答
\[\left\{\begin{array}{l}x=\frac{\sqrt{3}}{2}t^2-\frac{1}{2}t\\y=\frac{1}{2}t^2+\frac{\sqrt{3}}{2}t\end{array}\right.\]
であるので、
\[x+yi=(t^2+ti)\left(\frac{\sqrt{3}}{2}+\frac{1}{2}i\right)\]
が成り立つ。
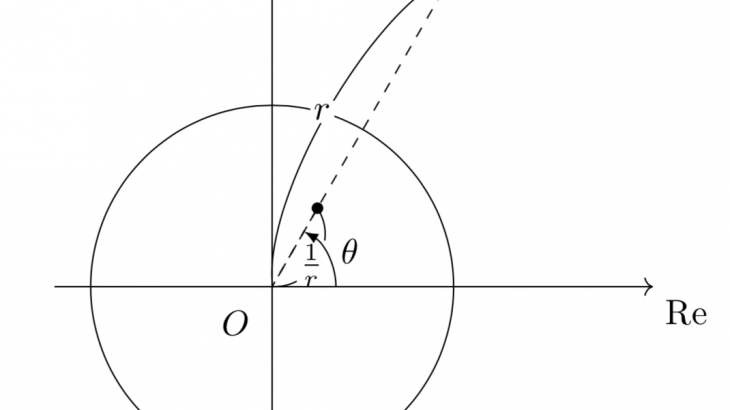
$t$が実数全体を動くとき$(t^2,t)$は$x=y^2$を描くので、求めるグラフはそれを原点を中心として$\frac{\pi}{6}$だけ回転させたものだと分かる。したがって、求めるグラフは以下のようになる。

解くときの注意点
パラメータについてベクトルを整理するというのは、
\[\left\{\begin{array}{l}x=\frac{\sqrt{3}}{2}t^2-\frac{1}{2}t\\y=\frac{1}{2}t^2+\frac{\sqrt{3}}{2}t\end{array}\right.\]
と与えられたものを、
\[\left(\begin{array}{c}x\\y\end{array}\right)=t^2\left(\begin{array}{c}\frac{\sqrt{3}}{2}\\\frac{1}{2}\end{array}\right)+t\left(\begin{array}{c}-\frac{1}{2}\\\frac{\sqrt{3}}{2}\end{array}\right)\]
と見ることを指します。旧課程にあった行列を習ったことがある人なら、
\[\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}\frac{\sqrt{3}}{2}&-\frac{1}{2}\\\frac{1}{2}&\frac{\sqrt{3}}{2}\\\end{array}\right)\left(\begin{array}{c}t^2\\t\end{array}\right)\]
と変形して、回転行列を左からかけて放物線を回転させていることがすぐにわかるはずです。
今の教育課程では行列は習わずに、代わりに複素数平面を用いて回転操作を行うことになっているので、与えられた式を
\[\begin{align*}x+yi=&t^2\left(\frac{\sqrt{3}}{2}+\frac{1}{2}i\right)+t\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\=&(t^2+ti)\left(\frac{\sqrt{3}}{2}+\frac{1}{2}i\right)\end{align*}\]
と見てあげることになります。
このようにして、パラメータによってベクトルを整理してあげることによって放物線を回転させたものが求めるべきグラフだということが一目瞭然ですね。
ただし、この解法は他の2つの解法と違って、特殊な解法であることに注意しましょう。
まとめ
・媒介変数表示とは、$x,\,y$が新たな変数(パラメータ)によって書き表す関数の定義のしかた
・媒介変数表示された関数のグラフの描き方には
1.パラメータを消去する
2.パラメータで微分して増減表を描く
3.パラメータについてベクトルを整理する
の3通りのやり方がある
・1のやり方が基本、2のやり方は万能、3がうまく使えるときは稀