・そもそも共通接線とは
・共通接線を求める問題5パターンとは何か
・それぞれのパターンの解き方
・各パターンに対応する例題とその解答・解説
そもそも共通接線とは?
共通接線とは2つのグラフに接する直線
共通接線とは、2つのグラフに同時に接する直線のことです。このグラフは曲線であれば何でもよく、2次関数や3次関数だけでなく、円や双曲線など様々なグラフがあります。
大学受験に共通接線の問題は頻出
大学受験数学において、共通接線に関する問題は頻出です。中堅校では単に共通接線を求めるだけの問題が出題され、東大をはじめとする難関大では、「共通接線が3本存在するような定数$a$の条件を求めよ」のような出題形式で、共通接線と解の配置問題を絡めた出題がされることが多いです。
近年では、2017年東京大学数学(理科)の第五問で共通接線に関する問題が出題されています。
入試問題に出される共通接線の問題は5パターンしかない
共通接線を求める問題に出てくる曲線は本当はなんでも良いはずなんですが、大学入試問題に出される共通接線の問題は私の経験上、共通接線を求める問題には5パターンしか存在しません。
共通接線を求める問題全パターンを把握しておけば怖いものは何もないですね!
そこで、この記事では、共通接線を求める問題5パターンが何なのかを解説してから、それぞれに対応する例題を出題し、その解答・解説を書いていきたいと思います!
共通接線の問題5パターンの解き方は?
大学入試数学に出される共通接線の問題はこの5パターンです!
共通接線の問題5パターン!
1.片方のグラフが2次関数
2.両方とも3次以上の関数
3.4次関数に2回接する接線
4.2つの円に接する接線
5.共通接線が指定された本数あるような定数の条件を求める
それぞれのパターンについて解き方を見ていきましょう!
片方のグラフが2次関数の場合の解き方
片方のグラフが2次関数だった場合は、
1.もう一方のグラフの接点の座標を設定する
2.微分を使って接線の式を求める
3.接線と2次関数を連立した式が重解を持つ条件を判別式で考える
の手順で解くことができます!
放物線が出てくる場合には、接するという条件を方程式の重解条件に言い換えて、判別式を使ってあげるのが簡単ということですね!
もう一方のグラフというのは2次関数でも3次以上の関数でも構いません。どちらも2次関数だった場合には、どちらの接点を設定しても解けます。
両方とも3次以上の関数の場合の解き方
両方のグラフが3次以上の関数だった場合は、
1.両方のグラフの接点の座標を設定する
2.微分を使って2つの接線の式を求める
3.接線の式の係数を比較して一致するための条件を考える
が解き方になります!
3次以上の関数しかない場合には判別式を使うことができなくなってしまうので、2本の接線の式が一致するという条件で共通接線を考えるんですね。
4次関数に2回接する直線の場合の解き方
厳密には共通接線ではないですが、1つの4次関数に2回接する直線を求めさせられる問題が出題されることもあります。この場合は、
1.接線の式を設定する
2.接点の$x$座標を$\alpha,\,\beta(\alpha<\beta)$と設定する
3.接線の式と4次関数を連立した式が$(x-\alpha)^2(x-\beta)^2$を因数に持つ条件から恒等式を立てる
4.2式の係数を比較する
と解くことになります。
共通接線絡みの問題の中ではこれが一番面倒でしょう。2回接するということで、重解条件を2回考えることになりますが、判別式を用いることはできないので、因数として$(x-\alpha)^2(x-\beta)^2$を持つということを利用しています。
ただし、「共通接線と4次関数によって囲まれた部分の面積を求めよ」という問題の場合には、
\[\int_{\alpha}^{\beta}(x-\alpha)^2(x-\beta)^2dx=\frac{1}{30}(\beta-\alpha)^5\]
によって面積を計算できるので、必要なのは、接線の式ではなく、$\alpha,\,\beta$の値であることに注意しましょう。
2つの円に接する直線の場合の解き方
今までのパターンとは打って変わって、$n$次関数ではなく、円が出てくる共通接線の問題もあります。この場合は、
1.接線の式を設定する
2.円の中心からの接線までの距離が半径に等しいことを点と直線の距離の公式によって立式する
によって解けます。
円では、接するという条件を考えるには、「中心と直線との距離が半径に等しい」という条件で考えるのが一番考えやすいんでしたよね。このとき、点と直線の距離の公式を用いることになります。
点と直線の距離の公式
直線$ax+by+c=0$と点$(x_1,\,y_1)$との距離$d$は、
\[d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\]
で求めることができる。
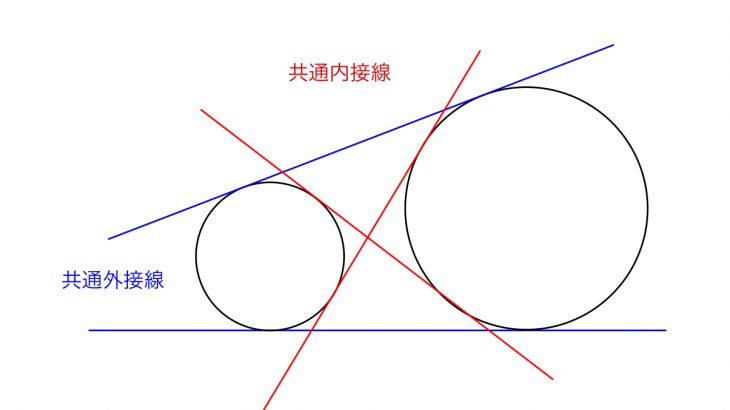
また、接線として出てくる直線は、最大で4本あることにも注意しましょう。(下図参照)
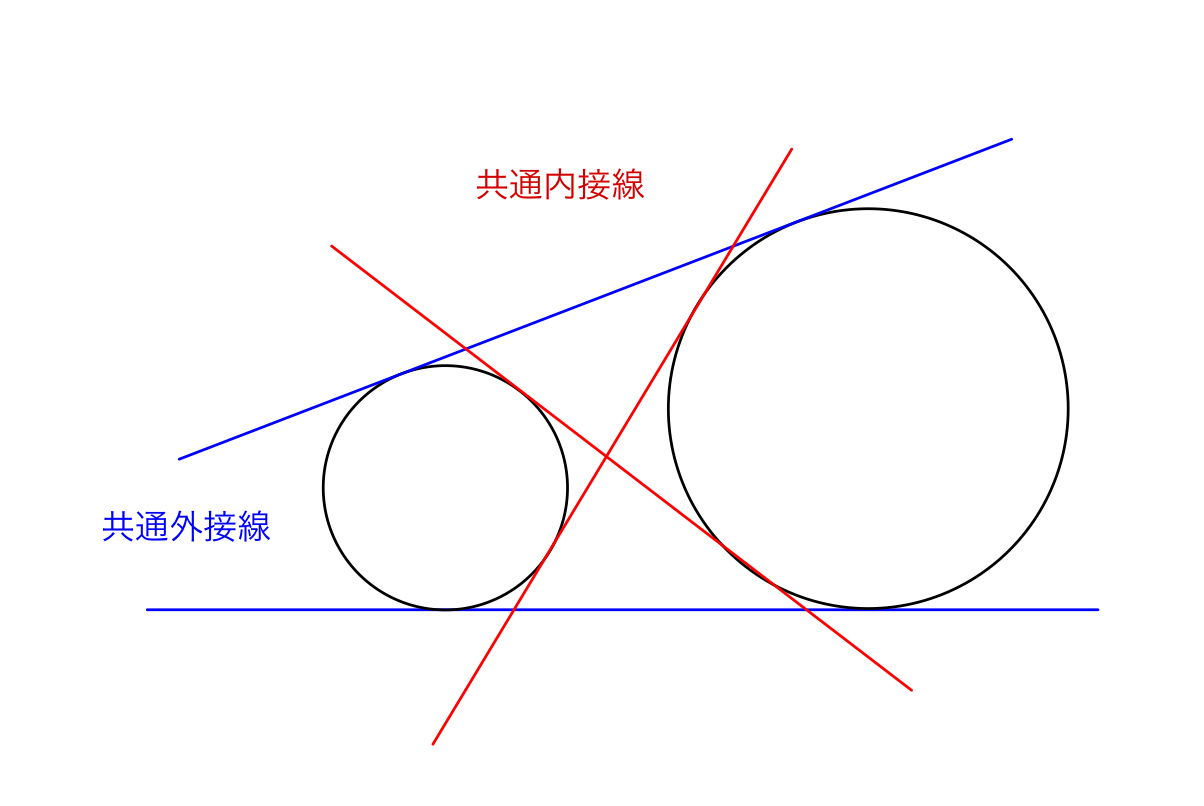
接線の同じ側に2円があるような共通接線を共通外接線、接線の逆側に2円があるような共通接線を共通内接線と呼びます。これらの名称を覚えておく必要はありませんが、4本の接線が出てくることは覚えておきましょう。先程、「最大で」とつけたのは2円が上図のように離れているときには4本の接線が存在しますが、共有点を持っていたりする場合には接線の本数は少なくなり、一方の円が他方の円に含まれている場合には共通接線は存在しなくなるからです。
片方のグラフだけが円で、もう一方のグラフは2次関数や3次関数だった場合には、2次関数や3次関数から微分を用いて接線の式を立てて、点と直線の距離の公式を使えばOKです。
共通接線が指定された本数あるような定数の条件を求める
冒頭でも説明しましたが、今までの説明してきたパターンの応用として、共通接線が指定された本数あるように定数の条件を定める問題もよく出題されます。これは難関大でよく見られる問題です。
この場合は、設定した接点の座標$t$の個数が共通接線の本数に等しいことを述べて、解の配置問題に帰着させることになります。解の配置問題については以下の記事で詳しく説明しています。
このタイプの問題には基本的に2次関数か3次関数しか出てきません。なぜなら、4次関数が出てきた場合には、4次関数に2回接する直線が存在するため、接点の座標$t$の解の個数と接線の本数が1対1に対応しなくなってしまい、議論がややこしくなるからです。
したがって、3次関数における解の配置問題を解く場合がほとんどだと思ってもらえればよいでしょう。
共通接線の問題5パターンの例題
共通接線の問題5パターンとその解き方を理解したら、それぞれに対応する例題を解いていきましょう!
例題1
$y=-2x^2$と$y=x^3-7x+4$の両方に接する直線は何本あるか答えよ。
解答
$f(x)=-2x^2,\,g(x)=x^3-7x+4$と名付ける。
$y=g(x)$上の点を$(t,\,t^3-7t+4)$とおくと、接線の方程式は、$g'(x)=3x^2-7$であることより、
\[\begin{align*}&y=(3t^2-7)(x-t)+t^3-7t+4\\\Leftrightarrow&y=(3t^2-7)x-2t^3+4\end{align*}\]
となる。これが、$y=f(x)$に接するとき、2式から$y$を消去した$x$の2次方程式
\[2x^2+(3t^2-7)x-2t^3+4=0\]
が重解を持つので、この判別式が$0$になることより、
\[\begin{align*}&(3t^2-7)^2-8(-2t^3+4)=0\\\Leftrightarrow&9t^4+16t^3-42t^2+17=0\\\Leftrightarrow&(t-1)^2(9t^2+34t+17)=0\\\Leftrightarrow&t=1,\,\frac{-17\pm2\sqrt{34}}{9}\end{align*}\]
ここで、3次関数に2度接する直線は存在しないので、$t$の解と接線は1対1に対応する。したがって、求める共通接線は、3本
解説
片方が2次関数のパターンなので、3次関数において微分をして接線の式を出してあげてから、2次関数と連立して、重解を持つ条件を考えています。求まった$t$の値が汚いので、代入して接線の式を求めるのは大変ですね。
もし仮に接線の方程式を要求された場合にはそのまま代入せずに、割り算をしてから代入するようにしましょう。
ある方程式$f(x)=0$の解$\alpha$を代入して、$g(\alpha)$を計算するとき、$g(x)$を$f(x)$で割り算してから、そのあまりに代入すると計算が楽になる。
今回の問題で言えば、$\frac{-17\pm2\sqrt{34}}{9}$というのは、$9t^2+34t+17=0$の解になっているので、$-2t^3+4$に代入する前に、
\[-2t^3+4=\left(-\frac{2}{9}t+\frac{68}{81}\right)(9t^2+34t+17)-\frac{2006}{81}t-\frac{832}{81}\]
と割り算を実行してあげてから、あまりの1次式に代入してあげる方が計算を少し楽にできます。
例題2
$y=x^3-x$と$y=x^3-x-4$の両方に接する直線の方程式を求めよ。
解答
$f(x)=x^3-x,\,g(x)=x^3-x-4$と名付ける。
$y=f(x)$上の接点を$(s,\,s^3-s)$、$y=g(x)$上の接点を$(t,\,t^3-t-4)$とおくと、接線の方程式は、それぞれ、
\[\left\{\begin{array}{l}y=(3s^2-1)x-2s^3\\y=(3t^2-1)x-2t^3-4\end{array}\right.\]
となる。共通接線となるとき、これら2式が一致すれば良いので、係数を比較して、
\[\begin{align*}&\left\{\begin{array}{l}3s^2-1=3t^2-1\\-2s^3=-2t^3-4\end{array}\right.\\\Leftrightarrow&\left\{\begin{array}{l}s=\pm t\\s^3=t^3+2\end{array}\right.\\\Leftrightarrow&\left\{\begin{array}{l}s=1\\t=-1\end{array}\right.\end{align*}\]
したがって、求める共通接線の方程式は、
\[\boldsymbol{y=2x-2}\]
解説
どちらも3次以上の関数なので、接線の式を2本立てて、係数が一致する条件を立式します。かなり上手く設定された条件でないと、きれいな接線の式が出てこないため、実際に接線の式を求められる機会は少ないでしょう。
そのため、パターンの5つ目として挙げた、共通接線の本数の議論と絡めた出題などがメインになります。
例題3
4次関数$y=x^4-2x^2-2x+1$に2度接する直線の方程式を求めよ。
解答
求める直線は$y$軸に平行でないので、$y=mx+n$とおくことができる。
$y=x^4-2x^2-2x+1$との接点の$x$座標を$\alpha,\,\beta(\alpha<\beta)$とおくと、2式から$y$を消去した4次方程式は$x=\alpha,\,\beta$において重解をもつので、2式から$y$を消去した4次方程式は、
\[x^4-2x^2-(2+m)x+1-n=(x-\alpha)^2(x-\beta)^2\]
と因数分解できる。
\[(右辺)=x^4-2(\alpha+\beta)x^3+(\alpha^2+\beta^2+4\alpha\beta)x^2\\-2\alpha\beta(\alpha+\beta)x+\alpha^2\beta^2\]
となるから、両辺の係数を比較して、
\[\left\{\begin{array}{l}\alpha+\beta=0\\\alpha^2+\beta^2+4\alpha\beta=-2\\2\alpha\beta(\alpha+\beta)=2+m\\\alpha^2\beta^2=1-n\end{array}\right.\]
第二式を変形して、
\[(\alpha+\beta)^2+2\alpha\beta=-2\]
これに第一式$\alpha+\beta=0$を代入して、
\[\alpha\beta=-1\]
これらを第三式、第四式に代入して、$m=-2,\,n=0$が分かる。
ここで、$\alpha+\beta=0,\,\alpha\beta=-1$より、解と係数の関係から、$\alpha,\,\beta$は$t$の2次方程式$t^2-1=0$の解なので、$\alpha=-1,\,\beta=1$とわかり、たしかに2接点が存在する。
したがって、求める接線は、
\[\boldsymbol{y=-2x}\]
解説
接線の式を設定するときには、$y$軸に平行な直線にならないことを確認し忘れないようにしましょう。直線の式を定めることができたら、上で説明した通りの解き方をしていけばOKです。
$\alpha$と$\beta$の対称性を意識すると、基本対称式の値だけ求めてあげれば接線の式は決定できますが、ここで注意したいのは、$\alpha,\,\beta$がたしかに異なる実数として求まるまで接線が本当に存在するかは保証されないという点です。
たとえば、$\alpha$と$\beta$が共役な複素数である場合には、基本対称式の値は実数値として求まりますが、接点の$x$座標は実数値でないといけないので接点は存在しないことになりますよね。そこで、実際に値を求めるか、$\alpha$と$\beta$を解に持つ2次方程式の判別式を考えるかする必要があります。上の答案では、2次方程式を作ってから実際に解いて接点の存在を確認しています。
例題4
2つの円$x^2+y^2=1,\,(x-2)^2+y^2=1$の両方に接する直線をすべて求めよ。
解答
求める直線は$y$軸に平行ではないので、$y=mx+n$とおくことができる。これが、$x^2+y^2=1$に接するとき、中心$(0,\,0)$からの距離が半径$1$に等しくなるので、点と直線の距離の公式より、
\[\frac{|n|}{\sqrt{m^2+1}}=1\Leftrightarrow n=\pm\sqrt{m^2+1}\]
同様にして、$(x-3)^2+y^2=1$に接する条件は、
\[\frac{|3m+n|}{\sqrt{m^2+1}}=1\Leftrightarrow 9m^2+n^2+6mn=m^2+1\]
$n=\sqrt{m^2+1}$を代入して、
\[\begin{align*}&9m^2+6m\sqrt{m^2+1}=0\\\Leftrightarrow&3m^2=- 2m\sqrt{m^2+1}\\\Leftrightarrow&m\leqq0,\,9m^4=4m^2(m^2+1)\\\Leftrightarrow&m=0,\,m=-\frac{2}{\sqrt{5}}\end{align*}\]
よって、
\[(m,\,n)=(0,\,1),\,\left(-\frac{2}{\sqrt{5}},\,\frac{3}{\sqrt{5}}\right)\]
また、$n=-\sqrt{m^2+1}$のときも同様にして、
\[(m,\,n)=(0,\,-1),\,\left(\frac{2}{\sqrt{5}},\,-\frac{3}{\sqrt{5}}\right)\]
したがって、求める共通接線の方程式は、
\[\boldsymbol{y=\pm1,\,y=\pm\frac{2}{\sqrt{5}}x\mp\frac{3}{\sqrt{5}}(複号同順)}\]
解説
円が出てくるので、接線の方程式をおいてから点と直線の距離の公式を使います。接線をおくときは先ほどと$y$軸に平行でないことを述べないといけません。
2円の中心間の距離は$3$で、半径の和は$2$なので、円同士で共有点は持っておらず、共通接線は4本求まります。
例題5
曲線$y=x^3$と曲線$y=x^2+x+c$との両方に接する直線が4本あるような$c$の範囲を求めよ。(一橋大)
解答
$y=x^3$上の接点の座標を$(t,\,t^3)$とおくと、接線の方程式は、
\[\begin{align*}&y=3t^2(x-t)+t^3\\\Leftrightarrow&y=3t^2x-2t^3\end{align*}\]
となる。これが、$y=x^2+x+c$に接するとき、これらから$y$を消去した2次方程式
\[x^2+(1-3t^2)x+c+2t^3=0\]
が重解を持つので、
\[\begin{align*}&(1-3t^2)^2-4(c+2t^3)=0\\\Leftrightarrow &9t^4-8t^3-6t^2+1=4c\end{align*}\]
となる。3次関数に二度接する直線は存在しないので、$t$の値が異なれば対応する接線も異なる。よって、共通接線が4本あることは、この方程式の実数解が4つあることと同値である。左辺を$f(t)$とおくと、
\[f'(t)=36t^3-24t^2-12t=12t(t-1)(3t+1)\]
であるから、増減表は以下のようになる。
\[\begin{array}{|c||c|c|c|c|c|c|c|} \hline x&\cdots&-\frac{1}{3}&\cdots&0&\cdots&1&\cdots\\\hline f'(x)&-&0&+&0&-&0&+\\\hline f(x)&\searrow&\frac{20}{27}&\nearrow&1&\searrow&-4&\nearrow\\\hline\end{array}\]
したがって、$y=f(t)$のグラフは以下のようになる。
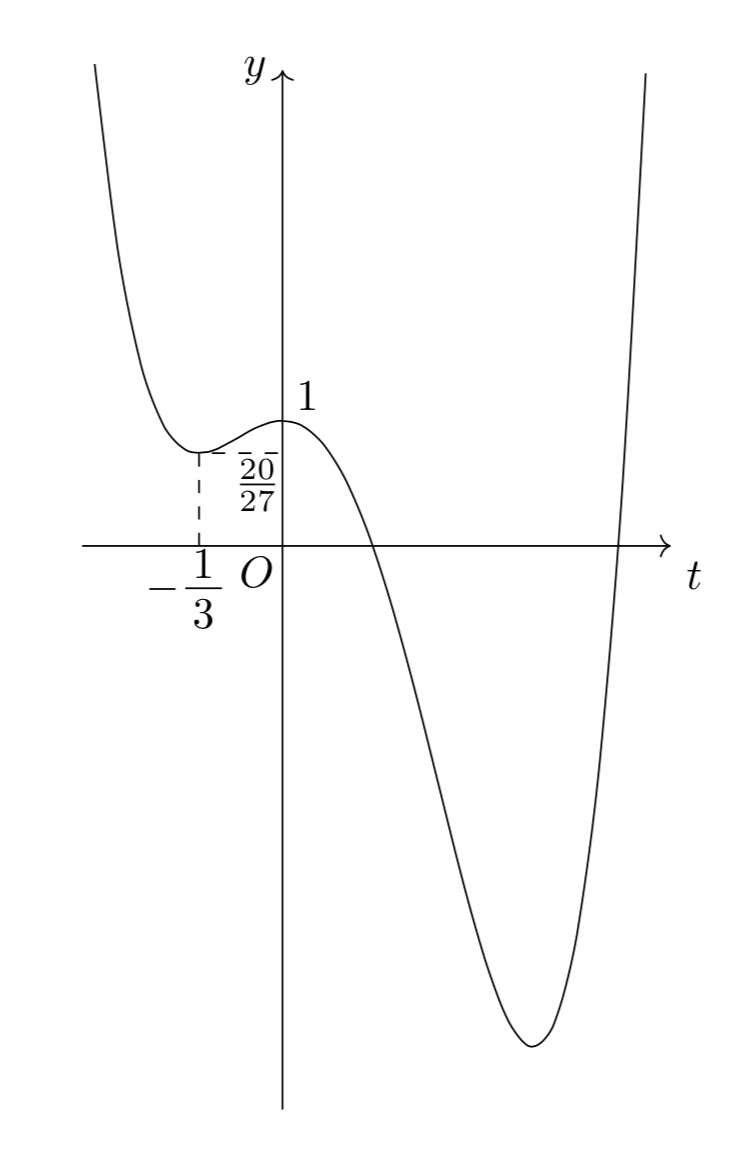
これと$y=4c$が異なる4つの共有点を持つような$c$の範囲は、
\[\frac{20}{27}<4c<1\Leftrightarrow \boldsymbol{\frac{5}{27}<c<\frac{1}{4}}\]
解説
3次関数と2次関数の共通接線の問題の応用です。接線の方程式を求めるときと作業は変わりませんが、判別式=0を考えたあとに出てくる$t$の4次方程式の解の個数が4個になる条件を考えていくことになります。
3次以上の関数の解の配置問題では、定数分離をしてあげてから、グラフを描き、共有点の議論に帰着させるんでしたね。解の個数と接線の本数が1対1に対応することを述べるのも忘れないようにしましょう。
まとめ
・共通接線とは2つのグラフに接する直線のこと
・共通接線の問題は2次関数が含まれるもの、3次以上の関数だけのもの、4次関数に2回接するもの、円が関わるもの、共通接線が決められた本数存在する条件を求めるものの5パターンある
・2次関数があれば重解条件を考える
・3次以上の関数だけのときは2つの接線が等しいことを用いる
・4次関数のときは因数として$(x-\alpha)^2(x-\beta)^2$が出てくることを用いる
・円は点と直線の距離の公式を使う
・接線の本数についての議論は解の配置問題に帰着させる