この記事を読むとわかること
・順像法・逆像法がどのようなものなのか
・順像法・逆像法を使った問題の解き方
・順像法・逆像法の図解
・順像法と逆像法の使い分け
順像法・逆像法とは?
順像法とはスライスして領域を求めるやり方
順像法とは、簡単に言えば、ある軌跡・領域を求めるために、その図形をスライスしたときに現れる線分の集まりとして図形の形を求めるやり方のことを指します。
より具体的には、$x$を固定してパラメータが変化したときの$y$の値域を求めるという操作を行います。
…とは言っても、言葉での説明ではいまいちピンとこないですよね。あとで、実際に問題を通して順像法を使った解き方を学ぶので、その時に理解すれば十分です。
順像法はファクシミリの原理、正像法、自然流とも呼ばれることがあります。
この4つの呼び名の中では、ファクシミリの原理という呼び方が最も順像法が何かを上手く言い表しているでしょう。FAXを送るときは、横に細かい線で区切って少しずつ読み込んでいきますよね。
順像法は、FAXと同じようにある図形を少しずつ区切って、最終的に全体像を把握するという手法です。
逆像法とは点が領域内にあるか判定する手法
逆像法とは、簡単に言えば、ある軌跡・領域を求めたいときに、ある点がその図形の中に含まれているかどうかを判定することによって、図形の形を把握するやり方のことを指します。
逆像法は逆手流とも呼ばれます。軌跡・領域の中で様々な手法の名前があって混乱してしまいそうですが、同じものの呼び方が複数あるだけであって、実際には逆像法と順像法という2つの手法しかありません。
順像法・逆像法を使って領域の問題を解こう!
以下の問題を、順像法・逆像法の2通りの解き方でやって、使い方を学んでいきましょう!
例題
実数$a$が$-1\leqq a\leqq 3$の範囲を動くとき、直線$y=(a-1)x+a^2$が通過する領域を求めよ。
順像法での解き方
順像法ではまずxを固定する
順像法で領域を求めるときには、まず$x$を固定して、$y$を$a$の関数と見ます。
順像法ではまず$x$を固定して$y$をパラメータ$a$の関数と見る
上の問題で、順像法を使うために$x$を固定すると、
\[y=a^2+xa-x\]
という$a$の2次関数として見ることができます。
パラメータaを動かしてyの値域を求める
次に、$a$を$-1\leqq a\leqq 3$の範囲を動かして$y$の値域を求めましょう!2次関数の値域を求める時には、平方完成すればOKですよね。平方完成すると、
\[y=a^2+xa-x=\left(a+\frac{x}{2}\right)^2-\frac{x^2}{4}-x\]
となるので、軸である$a=-\frac{x}{2}$と定義域$-1\leqq a\leqq 3$との位置関係で場合分けが生じます。最大値を取るのが定義域の右端か左端かが切り替わるのは、定義域のちょうど真ん中である$a=1$に対して軸がどちら側にあるか、最小値は、定義域の左にあるか、右にあるか、中にあるか、で場合分けされるので、結局、4通りの場合わけが必要になります。
順像法による解法の答案
では、以上のことを踏まえて実際に答案を書いていきましょう!
$x$を固定して、$y$を$a$の関数と見ると、
\[y=a^2+xa-x=\left(a+\frac{x}{2}\right)^2-\frac{x^2}{4}-x\]
という2次関数になる。
(i)$-\frac{x}{2}\leqq -1\Leftrightarrow x\geqq 2$のとき、
$a=-1$のとき最小値をとり$a=3$のとき最大値をとるから、$y$の動く範囲は、
\[-2x+1\leqq y\leqq 2x+9\]
となる。
(ii)$-1\leqq -\frac{x}{2}\leqq 1\Leftrightarrow -2\leqq x\leqq 2$のとき、
$a=-\frac{x}{2}$のとき最小値をとり$a=3$のとき最大値をとるから、$y$の動く範囲は、
\[-\frac{1}{4}x^2-x\leqq y\leqq 2x+9\]
となる。
(iii)$1\leqq -\frac{x}{2}\leqq 3\Leftrightarrow -6\leqq x\leqq -2$のとき、
$a=-\frac{x}{2}$のとき最小値をとり$a=-1$のとき最大値をとるから、$y$の動く範囲は、
\[-\frac{1}{4}x^2-x\leqq y\leqq -2x+1\]
となる。
(iv)$-\frac{x}{2}\geqq 3\Leftrightarrow x\leqq -6$のとき、
$a=3$のとき最小値をとり$a=-1$のとき最大値をとるから、$y$の動く範囲は、
\[2x+9\leqq y\leqq -2x+1\]
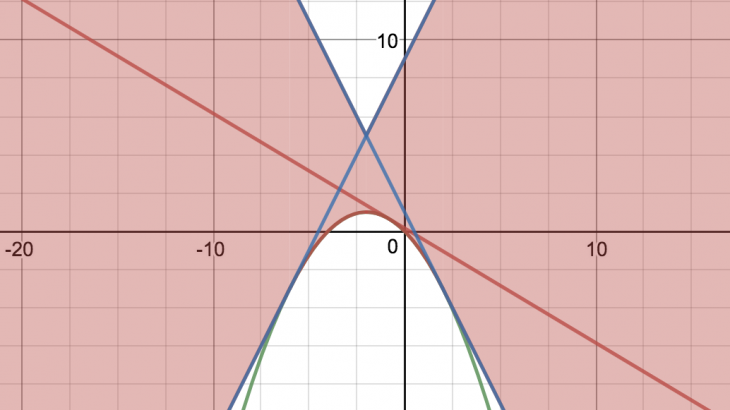
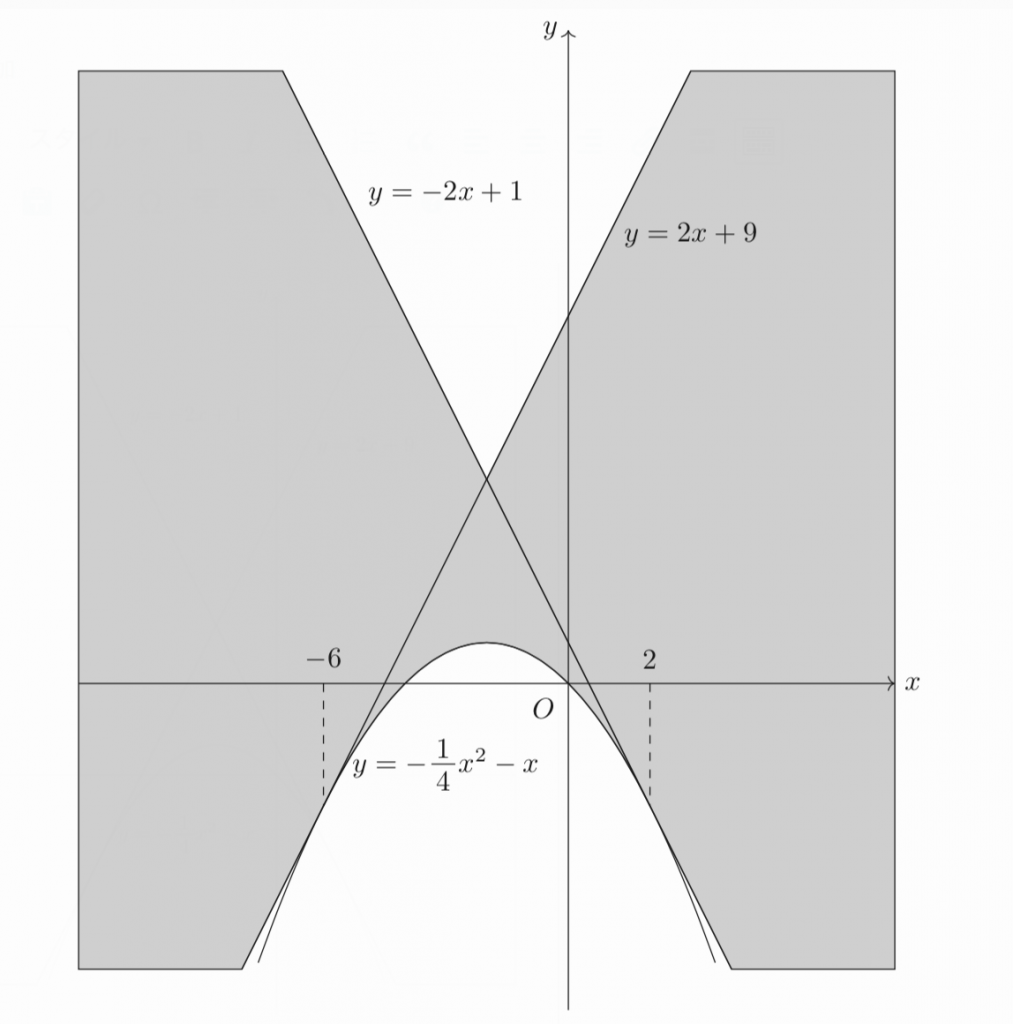
したがって、求める図形は下図の斜線部。(境界はすべて含む。)
逆像法での解き方
逆像法ではまず図形の方程式をパラメータの方程式と見る
逆像法で領域を求めるときには、まず与えられた図形の方程式をパラメータ$a$の方程式と見ます。
逆像法ではまず与えられた図形の方程式をパラメータ$a$の方程式と見る!
今回で言えば、
\[y=(a-1)x+a^2\Leftrightarrow a^2+xa-(x+y)=0\]
と変形して、$a$の2次方程式と見ます。
与えられた範囲に実数解を持つための条件を求める
この2次方程式が与えられた$-1\leqq a\leqq 3$の範囲に実数解を持つような条件を求めてあげれば、それが求めるべき$x,\,y$の条件になります。
決められた範囲に実数解を持つための条件を求めるのは、いわゆる解の配置問題ですね。
パラメータについての解の配置問題を解いて、$x,\,y$の条件を求める!
出てきた$x,\,y$というのがまさに求めたい軌跡・領域になります。
解の配置問題の解き方がわからないという方はこちら。
逆像法による解法の答案
逆像法で解くと以下のような短い答案になります。
これを$a$の2次方程式と見た時、$-1\leqq a\leqq 3$の範囲に少なくとも1つの解を持つ条件を求めればよい。
したがって、求める条件は、$a^2+xa-(x+y)=0$の左辺を$f(a)$、$f(a)=0$の判別式を$D$としたとき、
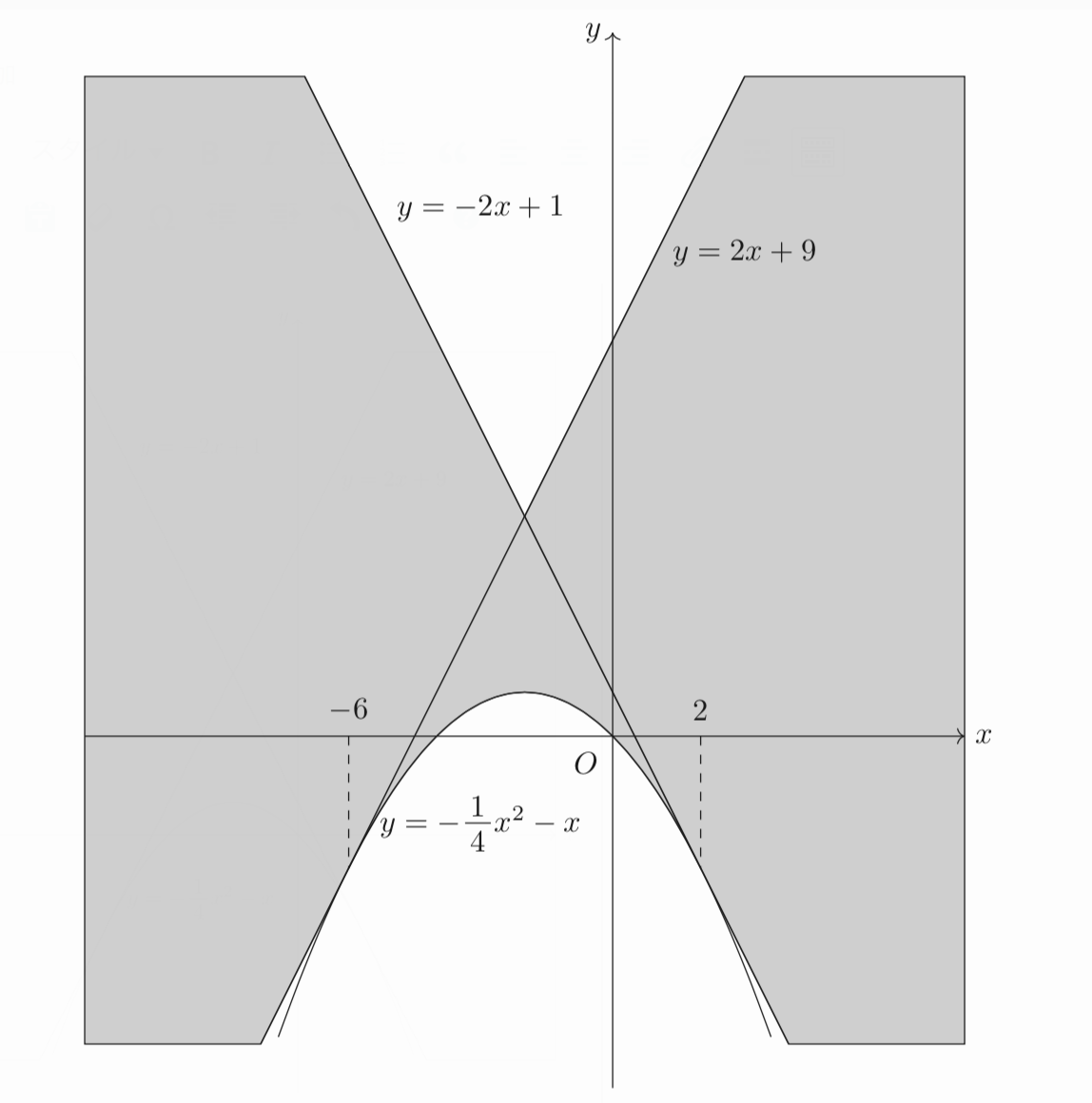
したがって、求める領域は以下の斜線部。(境界はすべて含む。)
【図解】順像法・逆像法は結局何をやっているのか
どちらの手法もいまいちイメージがつかない!という人のために、図で説明をしたいと思います!
順像法の図解
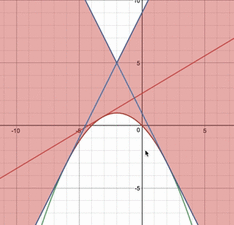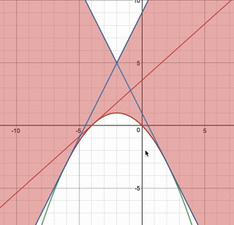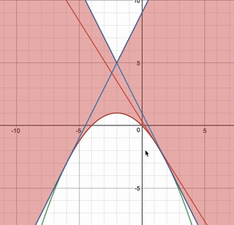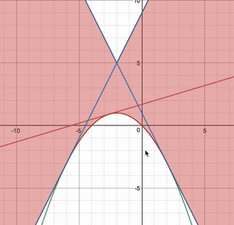
上の問題において、直線のパラメータ$a$を実際に動かすと、上図のように、どのような領域を通るのかは分かります。しかし、$a$をこんなに細かく動かしていくのは人間にはできないですよね。
そこで、順像法、つまり、縦にスライスして、FAXのようにこの領域を求めることを行っているのです。
例えば、$x=-3$で固定して、$y$の値域を求めるというのは、以下の図のようになります。

$x=-3$という直線と題意の直線との共有点の、$y$座標の値が変化し、その最大値が$-2x+1$、最小値が$-\frac{1}{4}x^2-x$となっていることがわかりますよね。
つまり、領域の上の境界と下の境界を$x$の関数として求めていくのが順像法のやり方なのです。
領域の上の境界、下の境界は$x$の値によって変化していきます。

$x=0$で固定した場合には上の図のようになります。この場合では、$y$の最大値が$2x+9$、最小値が$-\frac{1}{4}x^2-x$になっていますね。
このようにして、領域の上の境界、下の境界を場合分けをしつつすべて求めることを行っています。
逆像法の図解
逆像法では、ある点が上の赤い領域の中にあるのかということ判定することによって、領域を求めています。
例えば、$(x,\,y)=(4,\,8)$という点は、求めたい領域に入っているのか、図的に調べてみると、
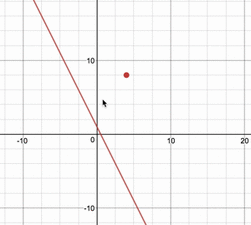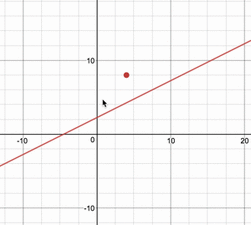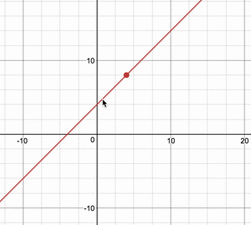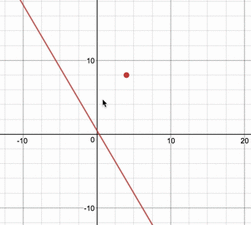
このように、直線が通過するときがあるので、領域の中にあることが分かります。
これは数式的にはどういう意味を持つのでしょうか?
$(x,\,y)=(4,\,8)$を与えられた直線の方程式に代入すると、
\[8=(a-1)4+a^2\Leftrightarrow a=2,\,-6\]
という2つの$a$の解が求まります。
$a=2$というのは$-1\leqq a\leqq 3$という範囲に入っているため、$a=2$となったときに題意の直線が$(4,\,8)$を通ることになるのです。
ちなみに、求める領域外の点である、$(x,\,y)=(-2,\,10)$を代入すると、
\[10=(a-1)\cdot(-2)+a^2\Leftrightarrow a=-2,\,4\]
という2つの解が求まり、たしかに$-1\leqq a\leqq 3$の範囲に解を持ちません。
このように、ある座標に対応する$(x,\,y)$を代入して$a$の方程式を解き、問題文で与えられた範囲に解を少なくとも1つの解を持っていれば、その点は求めたい領域に含まれることになります。
逆に言えば、問題文で与えられた範囲に少なくとも1つの解を持つような$x,\,y$の条件を解の配置問題を解くことによって求めれば、それがまさに求めるべき領域を表したものになるのです。
順像法と逆像法の使い分けは?
以上の説明でそれぞれの手法がどのようなものかはわかったと思いますが、これらの使い分けはどうすればよいのでしょうか?
順像法はすべての軌跡・領域の問題で使える
順像法は場合分けが多くなってしまうことが多く、受験生からは嫌われがちな手法ですが、どんな軌跡・領域の問題であっても順像法を使えば解くことができます。
順像法で解けない軌跡・領域の問題はない!
よって、順像法をマスターしてしまえば、軌跡領域の問題がわからなくて0点になるということはあり得ません。
軌跡・領域の問題は、逆像法によって劇的にはやく答えを求められることがしばしばありますが、そのせいか逆像法ばかり考えてしまって、順像法による解法を覚えてない受験生も多いです。
必ず、順像法をマスターするところから始めるようにしましょう。
逆像法はパラメータが1文字で2次以下、2文字で対称の時しか使えない
逆像法が使えるのはパラメータが2次以下の時に限られます。今回、例として挙げた問題ではパラメータ$a$について2次以下ですから、逆像法によっても解くことができます。
逆像法はいわゆる解の配置問題に帰着することによって、領域を求めるわけですから、3次以上の関数になると、途端に実数解を持つための条件やその範囲などが考えづらくなります。
ちなみに、2次関数のときであっても、パラメータの定義域の端にどちらも等号がついていないと、場合分けが多くなり、順像法よりもはやく解ける可能性が低くなります。
また、パラメータが2文字の場合には、パラメータが対称でない限り逆像法は使えません。これは、実数条件を考える際に、パラメータが対称でないと、同じ方程式の解として統一的に扱えないためです。
2文字の対称なパラメータの場合には、基本対称式の置き換えをして議論していくことになります。
2文字で対称なパラメータが出てくるのは、以下のような問題です。
$y=x^2+1(-1\leqq x\leqq 1)$上に$\mathrm{P}$、$y=x^2-1(-1\leqq x\leqq 1)$上に点$\mathrm{Q}$を取る。2点が与えられた範囲を自由に動くとき、線分$\mathrm{PQ}$の中点$\mathrm{M}$の動く領域を求めよ。
この場合、点$\mathrm{P}$の$x$座標と点$\mathrm{Q}$の$x$座標をパラメータに取ることになりますが、これらは、動く範囲が一緒であり、中点$\mathrm{M}$から見たときに対称であるので、逆像法によって解くことが可能です。
2文字のパラメータがあるのに対称でない場合は、同一の方程式の判別式で実数条件を考えられなくなってしまうので逆像法で解くことは無理になります。
以上をまとめると、
逆像法が使えるのは
・パラメータが1文字で2次以下のとき
・パラメータが2文字で対称なとき
まとめ
・順像法は一方向にスライスして図形を把握する手法のこと
・逆像法は点が領域に入っているかどうかを判定する手法のこと
・順像法は軌跡・領域のどんな問題に対しても使える
・逆像法が使えるのは、パラメータが1文字で2次以下、もしくは、2文字で対称なとき