この記事を読むとわかること
・じゃんけんが関わる確率の問題の解き方
・じゃんけんの確率が関わる入試問題
じゃんけんが関わる確率の問題の解き方は?
場合の数で考えるのが基本!
じゃんけんで勝敗が決まる確率やあいこになる確率を求める問題がありますが、題意の事象の数を、場に出される手のパターン全部が何通りあるかで割ることによって確率を求めるのが基本になります。
非常に簡単な例として、2人でじゃんけんをするときに、勝敗が決まる確率について、場合の数で考えてみましょう。
場に出される手の種類は、各人が3種類の手を出すことから、$3^2=9通り$となります。
勝敗が決まるパターンは、片方が3種類の手を出し、もうひとりがそれに勝つ手もしくは負ける手の2通りの手を出せばいいので、$3\times 2=6通り$あります。
したがって、求める確率は、
\[\frac{6}{9}=\frac{2}{3}\]
となります。
このようにして、場合の数を利用して確率を求めるのが一番考えやすいです。
じゃんけんの確率は
\[\frac{(題意の手のパターン数)}{(場に出される手のパターン数)}\]
によって計算すると良い!
じゃんけんを何度も繰り返すときは数列の知識が必要になる
じゃんけんを何度も繰り返して、勝敗が決まる確率を求める場合には、数列の知識が必要になってきます。特に、等比数列の和の公式や、確率漸化式の知識などが必要になってきます。
確率と数列の分野は相性が良く、2分野を融合した問題が良く出てくるので数列の知識が足りないという人は、もう一度勉強してみると良いでしょう。
じゃんけんの確率が関わる入試問題
習うより慣れろ!ということで、じゃんけんの確率が関わる入試問題をいくつか解いてみましょう。
問題1(n人のじゃんけんであいこになる確率)
$n$人で1回じゃんけんをする。このとき、あいこになる確率を求めよ。
解答
まず、$n$人でじゃんけんをするとき、場に出される手のパターンは、$3^n通り$。
$n$人でじゃんけんをするときに、勝敗が決まるのは、「場に2種類の手しか出ていないとき」であるから、例えば、グーとチョキしか場に出されない場合、各人はその2種類の手のうちのどちらかを出すので、$2^n通り$。
しかし、全員がグー、もしくは全員がチョキを出してしまうとあいこになるので、その場合を除いて$2^n-2通り$。
さらに、場に出される2種類の手の選び方は$_3C_2=3通り$あるので、勝敗が決まる場合の数は、$3(2^n-2)通り$ある。
あいこになる場合はその余事象なので、求める確率は、
\[1-\frac{3(2^n-2)}{3^n}=\boldsymbol{\frac{3^{n-1}-2^n+2}{3^{n-1}}}\]
解説
あいこになる場合というのは、パターンが多すぎて考えにくいです。そこで、その余事象である「勝敗が決まる場合」を考えて、その確率を1から引けば比較的簡単に確率を求めることができます。
勝敗が決まる場合というのは、「場に2種類の手しか出されない場合」であるという言い換えができればかなりスッキリ考えられます。ただし、全員が同じ種類の手を出してしまった場合はあいこになるので除かなければならないことに注意しましょう。
問題2(n回目で勝敗が決まる確率)
3人でじゃんけんをするとき、ちょうど$n$回目で勝敗が決る確率を求めよ。
3人でじゃんけんをするとき、ちょうど$n$回目で勝敗が決まるパターンは、
1.$n$回目で3人→1人になる
2.$k回目(1\leqq k\leqq n-1)$で3人→2人になり、$n$回目で2人→1人になる
の2パターンがある。
3人で一回じゃんけんをするときに誰か1人だけが勝つ確率は、
\[\frac{3\cdot 3}{3^3}=\frac{1}{3}\]
であり、あいこになる確率は、
\[1-2\cdot\frac{1}{3}=\frac{1}{3}\]
であるから、1.の場合の確率は、
\[\left(\frac{1}{3}\right)^{n-1}\cdot\frac{1}{3}=\left(\frac{1}{3}\right)^{n}\]
である。
また、$n\geqq 2$のとき、3人で一回じゃんけんをするときに誰か1人だけが負ける確率は$\frac{1}{3}$であり、また、2人で一回じゃんけんをするときに勝敗が決まる確率は$\frac{2}{3}$であるから、2.の場合の確率は、
\[\begin{align*}&\sum_{k=1}^{n-1}\left(\frac{1}{3}\right)^{k-1}\cdot\frac{1}{3}\cdot\left(\frac{1}{3}\right)^{n-k-1}\cdot\frac{2}{3}\\=&\sum_{k=1}^{n-1}2\left(\frac{1}{3}\right)^n\\=&\frac{2(n-1)}{3^n}\end{align*}\]
したがって、求める確率は、
\[\left(\frac{1}{3}\right)^{n}+\frac{2(n-1)}{3^n}=\boldsymbol{\frac{2n-1}{3^n}}\]
これは、$n=1$のときも成り立つ。
解説
じゃんけんを繰り返す問題のときには、勝敗が決まるまでの流れが複数パターンあることに注意しましょう。3人の場合には、3人→1人となるときもあれば、3人→2人→1人となる場合もありますよね。
そして、さらに気をつけなければならないのは、3人→2人→1人と人数が減っていくときには、$n\geqq 2$という条件が付くという点です!
勝敗が決まるパターンによる場合分けと$n$の値による場合わけをして、答えを求めてから、$n=1$のときも同じ式で表せるかどうか確かめる流れで書いています。
人数が徐々に減っていくパターンのときは、人数が減るタイミングがわからないので、すべての場合を足すときに数列のシグマ公式などを覚えておく必要性があります。今回は、3人のじゃんけんであいこになる確率と2人のじゃんけんであいこになる確率が等しいことから、たまたま等比数列の和の公式を用いる必要性は生じませんでしたが、基本的には何かの$k$乗の形が残って、等比数列の和の公式を使わなければいけなくなるということに注意しておきましょう。
確率漸化式を用いて解くことも可能です。以下に解答例を示しておきます。
別解
$n$回のじゃんけんのあと、3人が残っている確率を$p_n$、2人が残っている確率を$q_n$とおくと、3人で一回じゃんけんをするときに誰か1人だけが負ける確率は$\frac{1}{3}$、あいこになる確率は$\frac{1}{3}$であり、2人で一回じゃんけんをするときにあいこになる確率は$\frac{1}{3}$であることから推移図は以下のようになる。
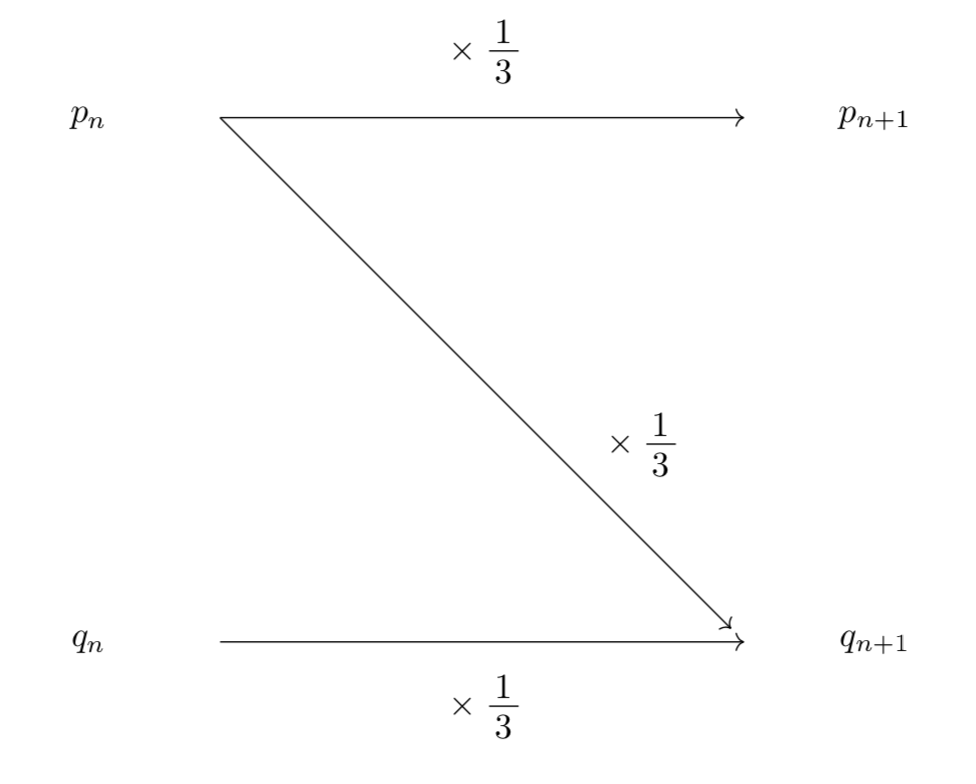
よって、
\[\left\{\begin{array}{l}p_{n+1}=\frac{1}{3}p_n\\q_{n+1}=\frac{1}{3}p_n+\frac{1}{3}q_n\end{array}\right.\]
が成り立つ。ここで、$p_0=1,\,q_0=0$であることから、
\[p_n=\frac{1}{3^n}\]
\[\begin{align*}&q_{n+1}=\frac{1}{3}q_n+\frac{1}{3^{n+1}}\\\Leftrightarrow &3^{n+1}q_{n+1}-3^nq_n=1\\\Leftrightarrow &3^nq_n=n\\\Leftrightarrow &q_n=\frac{n}{3^n}\end{align*}\]
となる。
ここで、$n$回目でちょうど勝敗が決まるとき、$n-1$回目のじゃんけんが終わったあとに残っている人数は2人か3人のどちらかである。よって、求める確率は、
\[\frac{1}{3}p_{n-1}+\frac{2}{3}q_{n-1}=\boldsymbol{\frac{2n-1}{3^{n}}}\]
確率漸化式を解いて、勝負が決まる直前の状態2パターンの確率をそれぞれ求めて、あとは3人→1人になる確率と2人→1人になる確率をそれぞれかけて足すだけです。
先ほどの解法と違って、$p_0,\,q_0$を持ち出すことによって、場合分けが不要になっているところが良い点ですね。
$q_n$を求めるときには、$r^n$が出てくるタイプの漸化式なので、両辺を$r^{n+1}$で割ってあげることによって$a_{n+1}=pa_n+q$型に帰着させています。今回は、等差数列型になっていますね。
$r^n$が出てくるタイプの漸化式の解き方を忘れてしまったという方は、こちらの記事で漸化式の解き方を総ざらいしておくとよいでしょう。
まとめ
・じゃんけんで勝敗が決まる確率を求めるときは場合の数を考えるのが基本
・じゃんけんを何度も繰り返す問題では等比数列の和の公式や確率漸化式の知識が必要になることが多い
・n人でじゃんけんをしてあいこになる場合を考えるときは余事象の考え方を使うと良い
・n回目のじゃんけんで勝敗が決まる確率を求めるときには人数の減り方で場合分けが生じる






