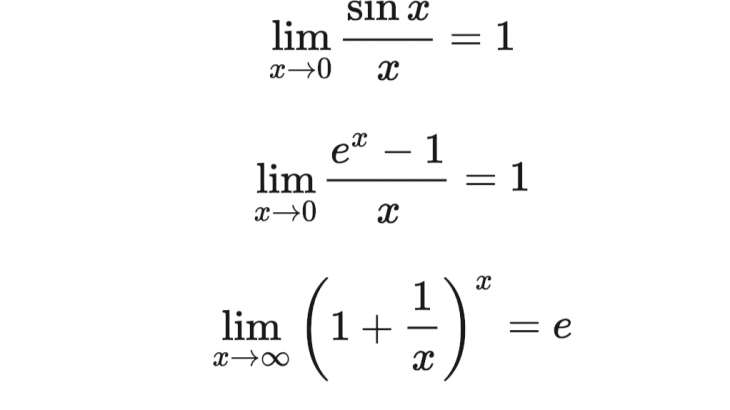極限公式で覚えておくべきはたった3つ！証明・導出・覚え方を教えます

大学受験数学で覚えておくべき極限公式は？

極限公式は3つだけ覚えておけばOK！

学校では様々な極限に関する公式を習いますが、極限公式は以下の3つだけを覚えておけば十分です。

この3つを覚えるだけなら簡単ですよね。

私は東大の2次試験で数学120点中104点を取っていますが、意識して暗記した極限公式はこの3つだけです。

極限公式の覚え方

上の3つの極限公式はそのまま覚えるのではなく「図で覚える」ことが非常に大事です。極限公式は基本的に傾きの比を表している式だと思いましょう。

下図を見てみると、1つ目の極限公式では$y=\sin{x}$と$y=x$が、2つ目の極限公式では$y=e^x-1$と$y=x$が$x=0$の近くで、傾きが等しくなっていますよね。

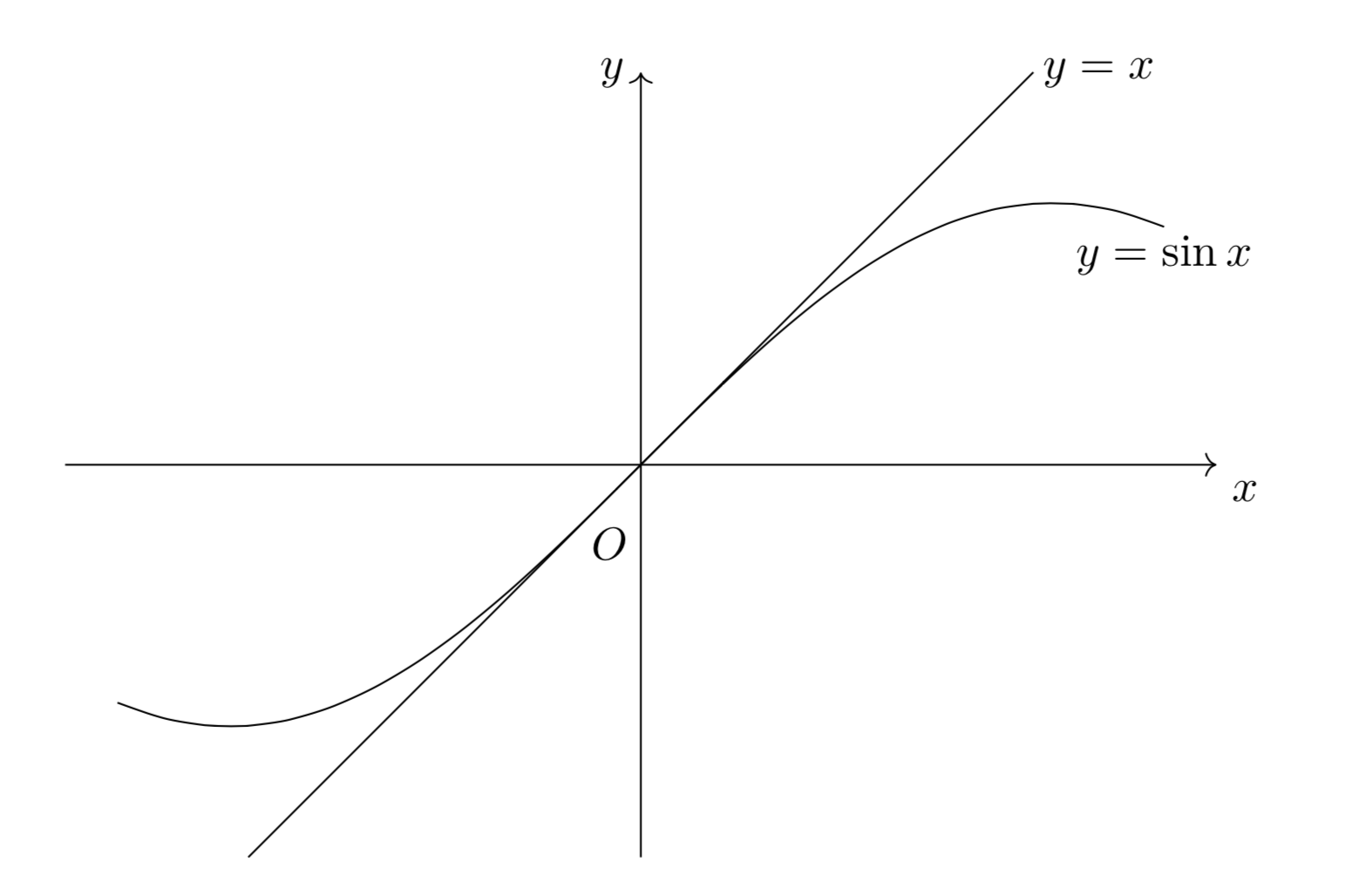
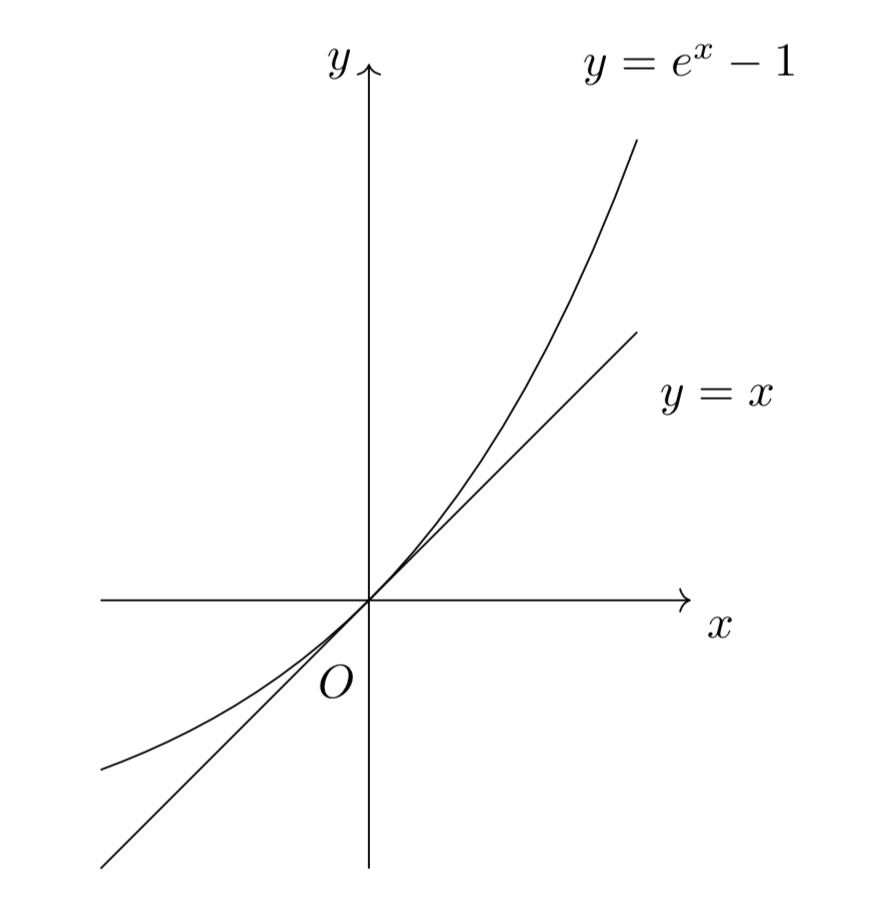
このようにして、図で視覚的に覚えておきましょう！

3つ目の極限公式は$e$の定義式なので、図で覚えるのではなく、そのまま覚えるしかありません。

その他の極限公式の導出のしかた

学校ではこれら以外にも極限公式を習うはずです。上の3つ以外の極限公式はどうやって覚えればいいのかについて説明していきます。

まず、
$$\lim_{x\to 0}\frac{1-\cos x}{x^2}=\frac{1}{2}$$

の公式は、
$$\begin{align*}\lim_{x\to 0}\frac{1-\cos x}{x^2}=&\lim_{x\to 0}\frac{1-\cos^2 x}{x^2(1+\cos x)}\\=&\lim_{x\to 0}\frac{\sin^2 x}{x^2(1+\cos x)}\\=&\frac{1}{2}\end{align*}$$

と変形すれば簡単に導くことができます。そもそも三角関数が出てくる極限公式は1つしか知らないのだから、それが使える形に変形しよう、と考えておけばこの変形は容易に思いつきますよね。

また、
$$\lim_{x\to 0}\frac{\log (1+x)}{x}=1$$

は、図を描いてみれば、
$$\lim_{x\to 0}\frac{e^x-1}{x}=1$$

の極限の公式を表した図を$y=x$に関して反転させただけだと分かります。

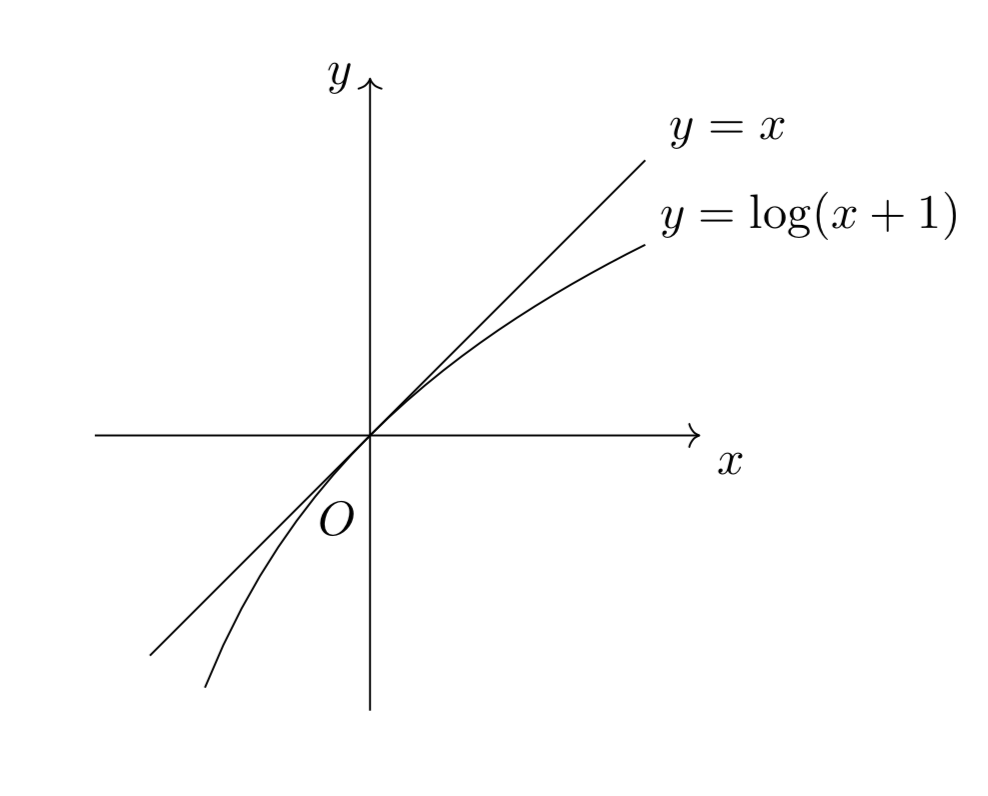
図で極限公式を覚えておくメリットはこんなところにも現れるんですね。

最後に、
$$\lim_{x\to \infty}\left(1-\frac{1}{x}\right)^x=\frac{1}{e}$$

については、3つ目の極限公式が使えるように、

$$\lim_{x\to \infty}\left\{\left(\frac{1}{1+\frac{1}{x-1}}\right)^{x-1}\right\}^{\frac{x}{x-1}}=\frac{1}{e}$$

と変形すれば導出することができます。

極限公式の証明のしかた

上で挙げた極限公式の1つ目と2つ目を証明しましょう！繰り返しになりますが、3つ目の公式は$e$の定義式なので、証明はありません。

lim(x→0)sinx/x=1の証明

これは、学校で証明を習った人も多いかと思いますが、実は学校で習う証明では不十分です。

この背景には循環論法というものがあり、以下の記事でこの極限公式の簡易的な証明、そして、循環論法にならない正しい証明のしかたについて説明しているので、気になる人は読んでみてください。

sinx/xの極限は？x→0とx→∞の場合を証明付きで東大医学部生が教えます！

lim(x→0)(e^x-1)/x=1の証明

2つ目の極限公式の証明は3つ目の極限公式から証明することができます。

まとめ