※以下の解答・解説は当ブログのオリジナルのものであり東京大学が公表しているものではありません。
私がおすすめする過去問題集について説明した記事はこちら↓
第一問
第一問は以下のような出題でした。

第一問の難易度分析
微分と極限に関する非常に易しい問題です。
指数関数の微分は$(a^x)’=a^x\log a$となることは知っていると思いますが、底にも$x$が含まれているので、公式は使えず、対数微分法を使わなければなりません。
あとは、対数微分法によって左辺と右辺の関数がそれぞれ単調に$e$に近づいていくということを示してあげればOKです。
第一問を解く上での考え方・ポイント
$\left(1+\frac{1}{x}\right)^x$のように、指数の部分にも底の部分にも$x$が含まれているような関数を微分するときには対数微分法を使う必要があります。
$f(x)^{g(x)}$の形の関数を微分するときには対数微分法を用いる!
対数微分法については以下の記事が詳しいです。
対数微分法を使うことによって示すべき不等式の左辺と右辺の関数を微分することができますね。ただし、対数を取るときには真数が正であることを確認しなければならないことに注意しましょう。
また、左辺も右辺も極限値は$e$になることが簡単に示せるので、左辺が単調増加し右辺が単調減少することが言えれば証明完了です。
以下、解答例になります。
\[f(x)=\left(1+\frac{1}{x}\right)^x\]
\[g(x)=\left(1+\frac{1}{x}\right)^{x+\frac{1}{2}}\]
とおく。$x$が正の実数であるとき、$f(x)$も$g(x)$も常に正の値を取る。よって、底を$e$とする対数をとることができて、
\[\begin{align*}&\log f(x)=\log \left\{\left(1+\frac{1}{x}\right)^x\right\}\\\Leftrightarrow &\log f(x)=x\log\left(1+\frac{1}{x}\right)\end{align*}\]
\[\begin{align*}&\log g(x)=\log \left\{\left(1+\frac{1}{x}\right)^{x+\frac{1}{2}}\right\}\\\Leftrightarrow &\log f(x)=\left(x+\frac{1}{2}\right)\log\left(1+\frac{1}{x}\right)\end{align*}\]
となる。これらの両辺を$x$で微分すると、
\[\begin{align*}&\frac{f'(x)}{f(x)}=\log\left(1+\frac{1}{x}\right)+x\cdot\frac{-\frac{1}{x^2}}{1+\frac{1}{x}}\\\Leftrightarrow &f'(x)=f(x)\left\{\log\left(1+\frac{1}{x}\right)-\frac{1}{1+x}\right\}\end{align*}\]
\[\begin{align*}&\frac{g'(x)}{g(x)}=\log\left(1+\frac{1}{x}\right)+\left(x+\frac{1}{2}\right)\frac{-\frac{1}{x^2}}{1+\frac{1}{x}}\\\Leftrightarrow &g'(x)=g(x)\left\{\log\left(1+\frac{1}{x}\right)-\frac{1+\frac{1}{2x}}{1+x}\right\}\end{align*}\]
ここで、$f(x)>0$、$g(x)>0$であるから、
\[A(x)=\log\left(1+\frac{1}{x}\right)-\frac{1}{1+x}\]
\[B(x)=\log\left(1+\frac{1}{x}\right)-\frac{1+\frac{1}{2x}}{1+x}\]
とおくと、$f'(x)$の符号は$A(x)$の符号に、$g'(x)$の符号は$B(x)$の符号に一致する。
\[\begin{align*}A'(x)=&\frac{-\frac{1}{x^2}}{1+\frac{1}{x}}-\frac{1}{(x+1)^2}\\=&-\frac{1}{x(x+1)^2}<0\end{align*}\]
より、$x$が正の実数であるとき、$A(x)$は単調減少し、
\[\lim_{x\to \infty}A(x)=0\]
であることも考えると、$A(x)>0$が言える。よって、$f(x)$は$x>0$において単調増加する。
同様に、
\[\begin{align*}&B'(x)=\frac{-\frac{1}{x^2}}{1+\frac{1}{x}}-\frac{-\frac{1}{2x^2}(x+1)-\left(1+\frac{1}{2x}\right)}{(x+1)^2}\\=&\frac{1}{2x^2(x+1)^2}>0\end{align*}\]
より、$x$が正の実数であるとき、$B(x)$は単調増加し、
\[\lim_{x\to \infty}B(x)=0\]
であることも考えると、$B(x)<0$が言える。よって、$g(x)$は$x>0$において単調減少する。
さらに、
\[\lim_{x\to \infty}f(x)=e\]
\[\lim_{x\to \infty}g(x)=\lim_{x\to \infty}f(x)\cdot \left(1+\frac{1}{x}\right)^{\frac{1}{2}}=e\]
となることも合わせると、題意の不等式は示された。
$f'(x)$や$g'(x)$の符号がわからないので、符号が不明な部分だけを取り出してさらに微分する作業が必要になっているところに注意しましょう。
第二問
第二問は以下のような出題でした。

第二問の難易度分析
非常に易しい確率の問題です。
$k$試合目で誰が待機しているかを文字でおいたりしたくなるところですが、問題の設定を読んでよく考えてみると、2試合目以降で大会が続くには、1つ前の試合で勝利した人が負けないといけないことから、規則的に勝利する人が変わっていくことがわかります。
すると、1試合目でAとBのどちらが勝ったかで場合分けをすることになります。
第二問(1)を解く上での考え方・ポイント
一瞬確率漸化式の問題かな、と思いたくなるところですが、具体的なケースを考えてみると、規則的に変化する非常に簡単な確率の問題であることに気づけます。
1試合目でAがBに勝利したとすると、次の試合はA対Cです。2試合目でAが勝ってしまうと大会終了となってしまうので、大会が続くにはCが勝利しなければなりません。
3試合目はC対Bとなりますが、Bが勝利しないと大会が終わってしまいます。
4試合目は再びA対Bとなります。
よって、勝利する人は「A→C→B→A→…」と周期的に変化していくことがわかります。
また、1試合目にBが勝利した場合には、「B→C→A→B→…」となるので、これらの2パターンで場合分けをしてあげればOKです。
以下、解答例になります。
ちょうど$n$試合目でAの優勝が決まるのは、題意より、各試合で勝利する人が「A→C→B→A→…→B→A→A」となるか「B→C→A→B→…→C→A→A」となるかの2パターンしかありえない。前者の場合は試合数が$3$で割って$2$余る数になり、後者の場合は試合数が$3$で割って$1$余る数になる。
以下、合同式の法を$3$とする。
(ii)$n\equiv 0$のとき、
Aがちょうど$n$回目で優勝する場合は存在しない。よって、確率は$0$になる。
(ii)$n\equiv 1$のとき、
「B→C→A→B→…→C→A→A」と勝者が推移していく場合しかないので、確率は、
\[\left(\frac{1}{2}\right)^n\]
となる。
(iii)$n\equiv 2$のとき、
「A→C→B→A→…→B→A→A」と勝者が推移していく場合しかないので、確率は、
\[\left(\frac{1}{2}\right)^n\]
となる。
したがって、求める確率は、
\[\left\{\begin{array}{l}\boldsymbol{n\equiv 1,\,2のとき\left(\frac{1}{2}\right)^n}\\\boldsymbol{n\equiv 0のとき0}\end{array}\right.\]
第二問(2)を解く上での考え方・ポイント
条件付き確率の定義にしたがって計算していくだけの問題です。条件付き確率の定義を復習しましょう!
ある事象Aが起こったという条件のもとでの、事象Bが起こる確率のことを条件付き確率と呼び、その条件付き確率$P_A(B)$は、
\[P_A(B)=\frac{P(A\cap B)}{P(A)}\]
によって求められる。
今回で言えば、Aが優勝するという事象が上の式におけるA、Aの最後の対戦相手がBであるという事象が上の式におけるBとなります。
それぞれの確率を求めるにはシグマ計算をすることになりますが、等比数列の級数を求めるだけなので特に問題はないでしょう。
以下、解答例になります。
(1)より、総試合数が$3m$回以下でAが優勝する確率は、$n\geqq 2$であることに注意すると、$m\geqq 2$のとき、
\[\begin{align*}&\sum_{k=2}^{m}\left(\frac{1}{2}\right)^{3k-2}+\sum_{k=1}^{m}\left(\frac{1}{2}\right)^{3k-1}\\=&\frac{\frac{1}{16}\left\{1-\left(\frac{1}{8}\right)^{m-1}\right\}}{1-\frac{1}{8}}+\frac{\frac{1}{4}\left\{1-\left(\frac{1}{8}\right)^{m}\right\}}{1-\frac{1}{8}}\\=&\frac{5}{14}-\frac{3}{28}\left(\frac{1}{8}\right)^{m-1}\end{align*}\]
$m=1$のときは$\frac{1}{4}$となるので、これは$m=1$でも成り立つ。
また、総試合数が$3m$回以下でかつ、Aの最後の対戦相手がBであるのは(1)の(ii)のパターンであるから、その確率は、$m\geqq 2$のとき、
\[\begin{align*}&\sum_{k=2}^{m}\left(\frac{1}{2}\right)^{3k-2}\\=&\frac{\frac{1}{16}\left\{1-\left(\frac{1}{8}\right)^{m-1}\right\}}{1-\frac{1}{8}}\\=&\frac{1}{14}\left\{1-\left(\frac{1}{8}\right)^{m-1}\right\}\end{align*}\]
$m=1$のときは$0$となるので、これは$m=1$でも成り立つ。
したがって、求める条件付き確率は、
\[\frac{\frac{1}{14}\left\{1-\left(\frac{1}{8}\right)^{m-1}\right\}}{\frac{5}{14}-\frac{3}{28}\left(\frac{1}{8}\right)^{m-1}}=\boldsymbol{\frac{8^m-8}{5\cdot 8^m -12}}\]
第三問
第三問は以下のような出題でした。

第三問の難易度分析
図形に絡めた、易しい微分の問題です。まずは、$S(a)$がどのような式になるかを求める必要がありますが、このときに、$\mathrm{R}_1,\,\mathrm{R}_2,\,\mathrm{R}_3$の値を愚直に求めるのではなく、相似などの図形的な関係に着目すると計算量を減らせます。
$S(a)$が求まったら、あとはただの1変数関数の最大最小問題なので、微分をすれば最小値は求められますね。
第三問を解く上での考え方・ポイント
3点$\mathrm{R}_1,\,\mathrm{R}_2,\,\mathrm{R}_3$の座標を求めたくなりますが、三角形$\mathrm{R}_1\mathrm{R}_2\mathrm{R}_3$は、点$\mathrm{Q}$を光源、$xy$平面をスクリーンとしたときの三角形$\mathrm{P}_1\mathrm{P}_2\mathrm{P}_3$の影のようなものになっているので、もし三角形$\mathrm{P}_1\mathrm{P}_2\mathrm{P}_3$が$xy$平面に平行であれば、2つの三角形は相似となり、簡単に面積が求められそうです。(実際には点$\mathrm{P}_3$が点$\mathrm{Q}$よりも上にあるので「影」ではありません。)
今回は点$\mathrm{P}_1,\,\mathrm{P}_2$の$z$座標は等しいものの、$\mathrm{P}_3$の$z$座標だけ異なっています。
そこで、直線$\mathrm{QP}_3$と平面$z=1$との交点$\mathrm{P}’_3$の座標を求めて、三角形$\mathrm{P}_1\mathrm{P}_2\mathrm{P}’_3$の面積を求めてあげれば、あとは相似を使って三角形$\mathrm{R}_1\mathrm{R}_2\mathrm{R}_3$の面積を求められそうです。
$S(a)$が求まったら、あとは微分して最小値を求めるだけですね!
最小値だけを求めれば良いので相加相乗平均の大小関係などの有名不等式も使えないか一度考えるべきですが、今回はうまく使えませんね。
直線$\mathrm{QP}_3$と平面$z=1$との交点を$\mathrm{P}’_3$とする。実数$k$を用いて、
\[\begin{align*}\overrightarrow{\mathrm{OP}’_3}=&\overrightarrow{\mathrm{OQ}}+k\overrightarrow{\mathrm{QP}_3}\\=&(k,\,0,\,(3-a)k+a)\end{align*}\]
と表すことができて、この$z$成分が$1$になればよいから、$1<a<3$に注意して、
\[(3-a)k+a=1\Leftrightarrow k=\frac{a-1}{a-3}\]
これを代入して、
\[\mathrm{P}’_3\left(\frac{a-1}{a-3},\,0,\,1\right)\]
が分かる。このとき、三角形$\mathrm{P}_1\mathrm{P}_2\mathrm{P}’_3$の面積は、
\[\left(1-\frac{a-1}{a-3}\right)\cdot 1 \cdot \frac{1}{2}=\frac{1}{3-a}\]
となる。また、$z=1$と$xy$平面は平行であるから、題意より、三角形$\mathrm{P}_1\mathrm{P}_2\mathrm{P}’_3$と三角形$\mathrm{R}_1\mathrm{R}_2\mathrm{R}_3$は相似であると分かるので、その相似比が$(a-1):a$であることも踏まえると、
\[S(a)=-\frac{a^2}{(a-3)(a-1)^2}\]
が分かる。
よって、$1<a<3$の範囲における$S(a)$の増減表は以下のようになる。
\[\begin{array}{|c||c|c|c|c|c|} \hline a&1&\cdots&2&\cdots&3\\\hline S'(a)&&-&0&+&\\\hline
S(a)&&\searrow&4&\nearrow&\\\hline\end{array}\]
したがって、求める最小値は、
\[\boldsymbol{4(a=2のとき)}\]
第四問
第四問は以下のような出題でした。

第四問の難易度分析
標準的な難易度の複素数平面の問題です。「鋭角三角形」という条件はどのように数式化できるか、そして、それを複素数平面において表すにはどうすればいいかを考える必要があります。
複素数平面上での角度に関する問題に慣れていた人にとっては易しかったでしょう。
第四問を解く上での考え方・ポイント
鋭角三角形の定義はもちろん「内角すべてが90度未満の三角形」ですから、$\mathrm{arg}$を用いてそれを数式化すればよいでしょう。例えば、$\angle\mathrm{ABC}$が90度未満という条件は、
\[-\frac{\pi}{2}<\mathrm{arg}\left(\frac{z^2-z}{1-z}\right)<\frac{\pi}{2}\]
と表せばOKですね。さらに、偏角が$-\frac{\pi}{2}$より大きく$\frac{\pi}{2}$よりも小さいというのは、「実部が正」という条件と等しいので、ある複素数$w$に対して、$w$の実部は$\frac{w+\bar{w}}{2}$であることを利用すればさらに条件を言い換えることができます。
鋭角三角形となる条件として、辺の長さを使った表し方もありますね。3辺の長さを$a,\,b,\,c(aが最も大きい)$としたときに、
\[a^2<b^2+c^2\]
が成り立つことが条件となります。今回は辺の大小関係が明らかにされていないので、3つ条件式を立てることになります。
どちらを使っても解くことは可能ですが、偏角を用いた議論が最もわかりやすいでしょう。
以下、解答例を示します。
$z=0,\,\pm 1$のときは3点のうち2つが一致してしまうので、$z\ne 0,\,\pm1$である。このもとで、三角形$\mathrm{ABC}$が鋭角三角形になることは、$\angle\mathrm{ABC},\,\angle\mathrm{BAC},\,\angle\mathrm{ACB}$がすべて$\frac{\pi}{2}$未満となることと同値である。
よって、
\[\left\{\begin{array}{l}-\frac{\pi}{2}<\mathrm{arg}\left(\frac{z^2-z}{1-z}\right)<\frac{\pi}{2}\\-\frac{\pi}{2}<\mathrm{arg}\left(\frac{z^2-1}{z-1}\right)<\frac{\pi}{2}\\-\frac{\pi}{2}<\mathrm{arg}\left(\frac{z-z^2}{1-z^2}\right)<\frac{\pi}{2}\end{array}\right.\]
である。さらに、これは$\frac{z^2-z}{1-z},\,\frac{z^2-1}{z-1},\,\frac{z-z^2}{1-z^2}$の実部が正である条件と等しいから、
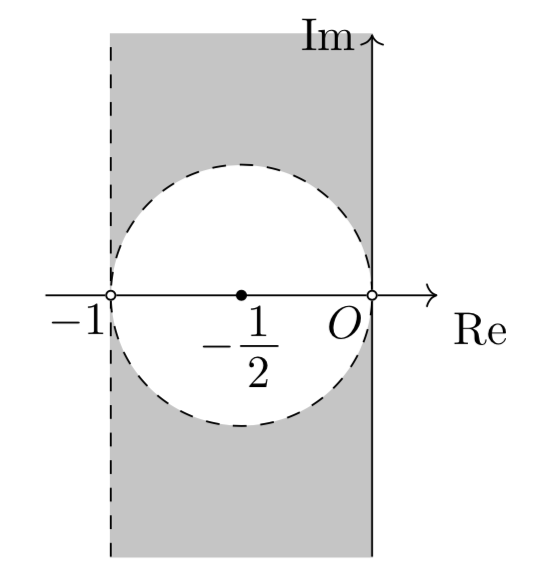
\[\begin{align*}&\left\{\begin{array}{l}\frac{z^2-z}{1-z}+\overline{\left(\frac{z^2-z}{1-z}\right)}>0\\\frac{z^2-1}{z-1}+\overline{\left(\frac{z^2-1}{z-1}\right)}>0\\\frac{z-z^2}{1-z^2}+\overline{\left(\frac{z-z^2}{1-z^2}\right)}>0\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}-(z+\bar{z})>0\\z+\bar{z}>-2\\\frac{z}{1+z}+\overline{\left(\frac{z}{1+z}\right)}>0\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}2\mathrm{Re}(z)<0\\2\mathrm{Re}(z)>-2\\z(1+\bar{z})+\bar{z}(1+z)>0\end{array}\right.\\\Leftrightarrow &\left\{\begin{array}{l}-1<\mathrm{Re}(z)<0\\\left|z+\frac{1}{2}\right|^2>\frac{1}{4}\end{array}\right.\end{align*}\]
これを複素数平面上に図示すると以下の斜線部。(ただし境界および白丸は含まない。)
第五問
第五問は以下のような出題でした。

第五問の難易度分析
やや難しい整数に関わる問題です。登場する文字の数が多く、問題文の把握に時間がかかった受験生が多かったかと思われます。
問題全体として問われていることは一貫して「ある整数のルートの小数部分」です。(3)の問題では、「整数のルートが整数にならないときに、小数部分が有限小数となることはありえない」ということが示されることになります。
さて、小問に分かれているときには各問題がどのような誘導になっているのかを考えることが重要になりますが、この問題の難しさは(1)や(2)の問題が(3)の誘導にはなっていないところにあります。
(2)までの議論を(3)にどう活かすかという視点でしか問題を見れていないと最後の問題で苦戦することになります。
第五問(1)を解く上での考え方・ポイント
与えられた不等式を変形することによって、$n$の不等式に変形することができます。ただし、不等式を2乗するときには両辺が$0$以上であることを確認し忘れないように気をつけましょう。
右辺の$+10^{k-1}$は$a_k$が$1$増えるという意味になっている(厳密には繰り上がりがあるかもしれないので$(a_k+1)$とは表記できない)ことを意識していれば、展開するときに$0.a_1a_2\cdots a_{k}+10^{k-1}$をひとかたまりで計算していくべきだと分かるでしょう。
得られた$n$についての不等式の範囲は非常に狭くなっているので、答えを求めるのは簡単ですね。
以下、解答例です。
すべての辺は正であるから、2乗しても同値性は崩れず、
左辺について、
右辺について、
となり、また、
\[0<(0.a_1a_2\cdots a_{k})^2<1\]
\[0<(0.a_1a_2\cdots a_{k}+10^{k-1})^2\leqq 1\]
であるから、題意を満たす$n$は、
第五問(2)を解く上での考え方・ポイント
(1)の問題では、与えられた不等式を$n$を2数が挟む不等式に直してあげると、それを満たす整数$n$が2つ見つかるという流れでした。
この不等式の”幅”は$10^k$に対応する部分が大きければ大きいほど広くなりますよね。そこで、(2)は簡単に言えば「(1)の$10^k$に対応する部分がもう少し小さくても条件を満たすものが見つかることを示してね」という問題になっています。
条件を満たす$m$が存在するための十分条件として、右辺と左辺の差が1よりも大きくなることが比較的容易に思いつくかと思います。2乗したときの係数として出てくる$2p$が$10^k$以上の数になることからこれは簡単に示せそうですね。
以下、解答例です。
すべての辺は正であるから、2乗しても同値性は崩れず、
左辺について、
\[\begin{align*}&(p+0.a_1a_2\cdots a_{k})^2\\=&p^2+2p(0.a_1a_2\cdots a_{k})+(0.a_1a_2\cdots a_{k})^2\end{align*}\]
右辺について、
となる。ここで、右辺と左辺の差を考えると、$p$が$5\cdot10^{k-1}$以上の整数であれば$2p$は$10^k$以上の整数となるので、
となる。したがって、
を満たす整数$q$を定めると、
が成り立つので、$m=q$とすれば条件は成り立つ。
したがって、題意成立。
第五問(3)を解く上での考え方・ポイント
難易度分析の項でも述べましたが、この問題は(1)や(2)と関わりが深そうに見えて、実はほぼ独立した問題になっています。この問題によって「(2)の左側の不等号の等号が成立することはない」ということがわかりますが、(2)で示した事実を応用するわけではありません。
さて、(3)の問題は言い換えれば「$\sqrt{s}$が整数にならないとき、その小数部分は有限小数にならない」ことを示す問題となりますが、これは、$\sqrt{s}$が無理数になるのが理由であることはすぐにわかると思います。
よって、「$\sqrt{s}$が整数にならないとき、その小数部分は有理数にならない」というもう少し強い条件が言えそうですね。
したがって、背理法によって$\sqrt{2}$が無理数であることを示すときとほとんど全く同じ手順で証明を展開していけば題意は示されます。
以下、解答例です。
$\sqrt{s}-[\sqrt{s}]=0.a_1a_2\cdots a_{k}$をみたす正の整数$s$の存在を仮定する。$0.a_1a_2\cdots a_{k}$は正の有理数、$[\sqrt{s}]$は整数であるから、互いに素な自然数$b,\,c$を用いて、
\[\sqrt{s}=\frac{c}{b}\]
とおくことができる。両辺2乗して、
\[s=\frac{c^2}{b^2}\]
となるが、$s$は自然数で$b,\,c$は互いに素より、$b=1$が必要。このとき、$\sqrt{s}$は整数となるので、$a_k\ne 0$であることに反しこれは矛盾。
したがって、元の仮定が誤りであり、$\sqrt{s}-[\sqrt{s}]=0.a_1a_2\cdots a_{k}$をみたす正の整数$s$は存在しないことが示された。
第六問
第六問は以下のような出題でした。

第六問の難易度分析
標準的な難易度の空間、積分に関する問題です。ただし、計算量が多いため、完答は難しかったかと思います。空間に関する問題で大事なのは空間のまま考えず、適切な平面で考えることです。
空間図形に関する問題は適切は平面に落とし込んで考える!
今回の問題は、与えられた条件がすべて$z$軸に関する回転対称性を持っていることに着目すると、たとえば$xz$平面上での線分$\mathrm{AB}$が通過する範囲を求めてからそれを回転させればいいことに気づけるでしょう。
東大は立体図形の問題、特に求積問題をよく出す傾向にあるので、こういった問題は絶対に完答したいところです。
第六問を解く上での考え方・ポイント
回転対称性に着目して、$xz$平面上でまず考えたりすることが重要であることはすでに述べましたが、さらに、回転体の体積を積分によって求めるわけなので、$z$軸に垂直に切ったときに出てくる線分の長さがどのようになるかが必要になります。
しかしながら、点$\mathrm{B}$の$z$座標から他の座標を考えていくのは大変そうです。そこで、線分$\mathrm{AB}$と$z$軸のなす角を文字で置いて、極方程式を求める要領で点$\mathrm{B}$の座標を求めるのがよいでしょう。
体積を求めるときには角度ではなく$z$で積分することになるので、置換積分をする必要性が出てきます。
下の動画のように線分が動いていくことがある程度イメージできると、比較的簡単に解き進められたかと思います。

以下、解答例です。
$K$は$z$軸を中心軸とする回転体になるので、まず$xz$平面上で$\mathrm{A}$が$x\leq0$の範囲にあるときの線分$\mathrm{AB}$の動く範囲を求めて、それを回転させればよい。
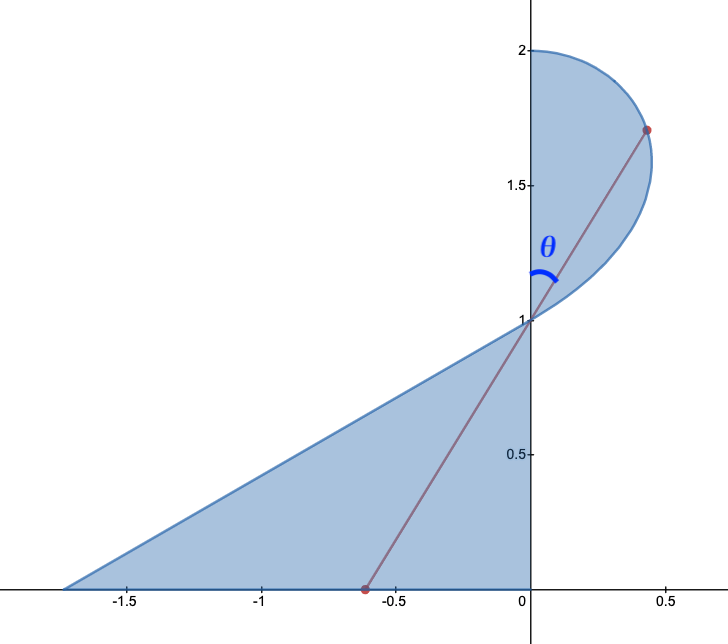
上図のように、$\overrightarrow{\mathrm{AB}}$と$z$軸の正方向のなす角を$\theta(0\leqq \theta \leqq \frac{\pi}{3})$とおくと、線分$\mathrm{AC}$の長さは$\frac{1}{\cos\theta}$となるので、
\[\mathrm{CB}=2-\frac{1}{\cos\theta}\]
が分かる。よって、点$\mathrm{B}$の座標は、
\[(x,\,z)=\left(2\sin\theta-\tan\theta,\,2\cos\theta\right)\]
となる。$2\cos\theta$は$0\leqq \theta \leqq \frac{\pi}{3}$の範囲で$\theta$に対して単調に減少するので、$K$のうち$z\geqq 1$の範囲にある部分の体積は、
\[\int_{1}^{2}\pi\left(2\sin\theta-\tan\theta\right)^2dz\]
と表せる。ここで、$z=2\cos\theta$と置換すると、
途中で点$\mathrm{B}$の$z$座標の単調性について触れているのは点$\mathrm{B}$の軌跡が例えば下図のようになってしまう場合に、体積の立式のしかたが変わってしまうからです。(こういうケースでは置換積分をしたあとには上と全く同じ式になることが知られていますが、$z$座標が増加しているときと減少しているときを分けて立式しなければなりません。)
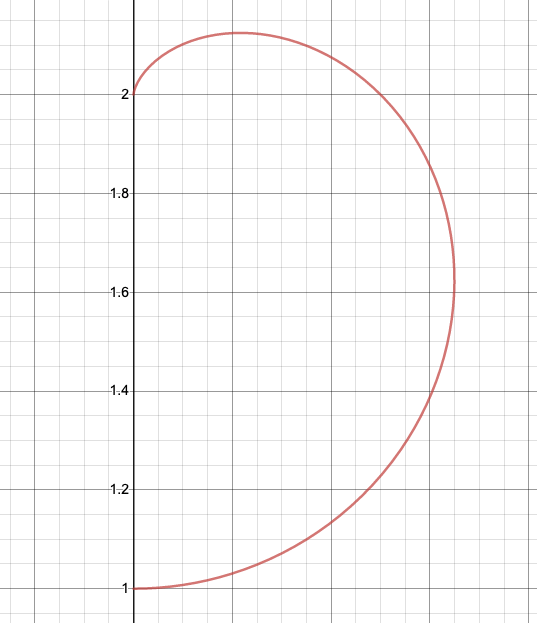
単調性がない場合の回転体の求積の例は以下の記事に出てくるので、興味がある方は読んでみてください。
また、置換積分したあとに出てくる$\sin^3\theta$の部分は3倍角の公式を用いて積分できる形に変形しています。
3倍角の公式
\[\cos3\theta=4\cos^3\theta-3\cos\theta\]
\[\sin3\theta=-4\sin^3\theta+3\sin\theta\]
まとめ
特段難しい問題はなかったものの、計算量が比較的多く、満点を取るのはなかなか難しいでしょう。特に第六問は難易度こそ高くないものの、計算量が多く、正しい答えを短時間で出せた受験生は多くないと思われます。
理三志望であれば、第6問で10点失点、他での失点を10〜20点程度に抑え、90〜100点を狙いたい内容です。理一・理二志望であれば、第6問は時間がかかると判断して他の5問に時間を割いた上で4完もしくは3完2半を狙って70点〜80点を狙いたいでしょう。
この年度は新課程に変わってから初めて複素数平面の問題が出た時であったという点で、難易度の割には苦しんだ受験生が多かったのではないかと推測しますが、難易度としてはそこまで高くないので、間違えたところがあればしっかり復習しておきましょう!





