数学的帰納法とは？入試問題付きで全5パターンをわかりやすく解説！

数学的帰納法とは？

数学的帰納法とは証明手法の1つ

数学的帰納法とは、「ある命題がすべての自然数$n$に対して成立すること」を「$n=1$のときについて成り立つこと」と「$n=k(kは自然数)$のときに成立するならば$n=k+1$のときにも成立すること」の2つから証明するという手法に代表される証明手法のことです。

例えば、人がたくさん一列に並んでいて、「先頭の人は眼鏡をかけている」という事実と「ひとつ前の人が眼鏡をかけているなら、その後ろの人も眼鏡をかけている」という法則が成り立っているとすれば、全員が眼鏡をかけているということがすぐにわかりますよね。これが数学的帰納法のざっくりとしたイメージになります。

数学的帰納法は実は演繹

数学的帰納法は「帰納」と名前についていますが、実際は自然数の性質を利用した演繹的な議論になっています。そもそも、帰納とは、個別具体的な事例から法則を”推定”する議論のしかたであり、必ず正しいと言えるものを導くことができません。数学的帰納法によって”証明”されたことは必ず正しいものなので、この時点で帰納的な議論とは性質が違うものだと分かるでしょう。

数学的帰納法の論理は、$n=1$のとき正しいなら、$n=2$のときも正しくなって、それならば$n=3$のときも正しくて…と、それぞれのケースが順番に正しいことが示されていくような構造になっていることから、個別具体的な事例を一つずつ見ていく帰納的な議論に似ており、数学的”帰納”法と名前がついたようです。

大学入試で使う数学的帰納法3パターン

大学入試数学で問われる数学的帰納法には基本的に以下の3パターンしかないと思ってよいでしょう。

それぞれについて例題付きで解説していきます！

n=kのときの成立を仮定するパターン

最もオーソドックスなタイプの帰納法です。例題として以下の問題を考えましょう。

このシグマ公式の証明は以下の記事の通り、和の中抜けを用いた証明方法が有名ですが、数学的帰納法によって証明することもできます。

シグマの公式(2乗、3乗、4乗)の証明は？数列の和はこれでマスター！

$n=1$のときにこれが成り立つことを示してあげてから、$n=m(mは自然数)$のときの成立を仮定して$n=m+1$のときにも成立することを示します。

結論がわかってれば、(ii)の議論において真面目に計算するまでもなく、$\frac{1}{6}m(m+1)(2m+1)+(m+1)^2$と書いた直後に、示したい式に$n=m+1$を代入したものを書いてしまえばOKですね！

n=k,k+1のときの成立を仮定するパターン

$n=k$のときの成立を仮定しても上手く数学的帰納法が機能しないことがあります。たとえば以下の例題のようなときです。

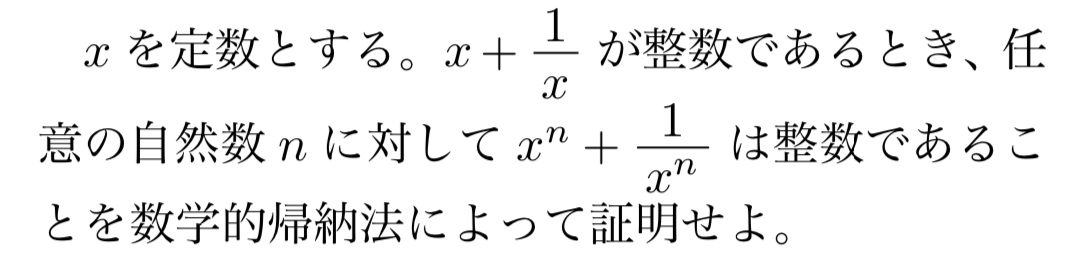
この問題の場合、$n=k(kは自然数)$の場合の成立を仮定して$n=k+1$のときの成立を示そうとすると、

$$\begin{align*}&x^{k+1}+\frac{1}{x^{k+1}}\\=&\left(x+\frac{1}{x}\right)\left(x^k+\frac{1}{x^k}\right)-\left(x^{k-1}+\frac{1}{x^{k-1}}\right)\end{align*}$$

となり、$\left(x+\frac{1}{x}\right)\left(x^k+\frac{1}{x^k}\right)$の部分は整数であることが示せても、$x^{k-1}+\frac{1}{x^{k-1}}$が整数であることが示せなくて困ってしまいます。

つまり、この場合は2つ前の成立までを仮定した状態でないと示せないパターンというわけです。

そこで、$n=1,\,2$のときの成立を確認したあと、「$n=k,\,k+1$の成立を仮定して、$n=k+2$のときの成立を示す」という作業をやっていくことになります。$n=2$のときの成立を確認しないといけないことにも注意しましょう。

n≦kのときの成立を仮定するパターン

最後は、$n\leqq k(kは整数)$のときの成立を仮定しなければならないパターンです。これは、上の2つと比べると出題頻度はかなり劣りますが、数列の第一項から第$n$項までをすべて使って次の項が定義されているタイプの漸化式と合わせてよく出題されます。以下の例題を考えてみましょう。

漸化式の問題ですが、普通に漸化式を解くことができなさそうなパターンでは、一般項を予測してから数学的帰納法によって示すのがよいのでした。漸化式の解き方については以下の記事にまとめてあります。

漸化式の解き方は？全10パターンを例題付きでわかりやすく東大医学部生が解説！

今回も一般項を予測して数学的帰納法によって示しましょう！

与えられた漸化式に$n=1$を代入してみると、$a_1>0$であることに注意して、

$$a_1^2=a_1^3\Leftrightarrow a_1=1$$

となります。同様に$a_2$や$a_3$も求めていくと、$a_2=2$、$a_3=3$が得られます。そうすると、一般項が$a_n=n$となるのではないか？と推測できますよね。

あとはこれを数学的帰納法によって示すことになります。このとき、$n=k$のときを仮定するだけでは不十分で、$a_{k+1}$を求めるには$a_1$から$a_k$まですべてが必要になることに気づきます。そこで、$n\leqq k$において成立することを仮定するという帰納法のパターンを使うことになります。

特殊な数学的帰納法の2パターン

ここでは特殊な数学的帰納法のパターンを扱います。先ほど説明したパターンはすべて$n$が大きくなる方向に論理が展開していく帰納法でしたが、ここでは逆に$n$が小さくなる方向に議論していくパターン2つを取り上げます。

それぞれについて例題を使いながら説明していきます。

無限降下法

無限降下法とは、背理法と数学的帰納法を組み合わせた証明の手法のことです。以下の例題を考えてみましょう。

フィボナッチ数列の隣り合う項は互いに素であることを示す問題です。「互いに素」であることとは「1以外の公約数を持たない」ことなので、「否定的な命題は背理法が有効なことが多い」という鉄則にしたがって、背理法の利用を考えたいところです。

そこで、$a_k$と$a_{k+1}$が互いに素でないような自然数$k$が存在すると仮定します。その時の最大公約数を$g$とすれば、このとき、与えられた漸化式から$n=k-1$のときもその公約数を約数に持つので$a_k$と$a_{k-1}$も$g$を公約数に持つことが言えます。同様の議論を繰り返していけば$a_1$と$a_2$のときも$g$を公約数に持つことが言えますよね。

しかし、これは$a_1$と$a_2$の最大公約数が$1$であることと矛盾するので、元の仮定が誤りだとわかります。

このように、背理法の仮定として$n=k$のときの不成立を仮定して、そこから数学的帰納法のような議論から$n=1$のときまで遡って矛盾を導くという手法を無限降下法と言います。

双方向帰納法

双方向帰納法とは、大きな$n$について成立することを数学的帰納法によって示してから、$n$が小さくなる方向に再び数学的帰納法を適用することによって示すという議論のしかたのことです。以下の例題を見ながら学びましょう。

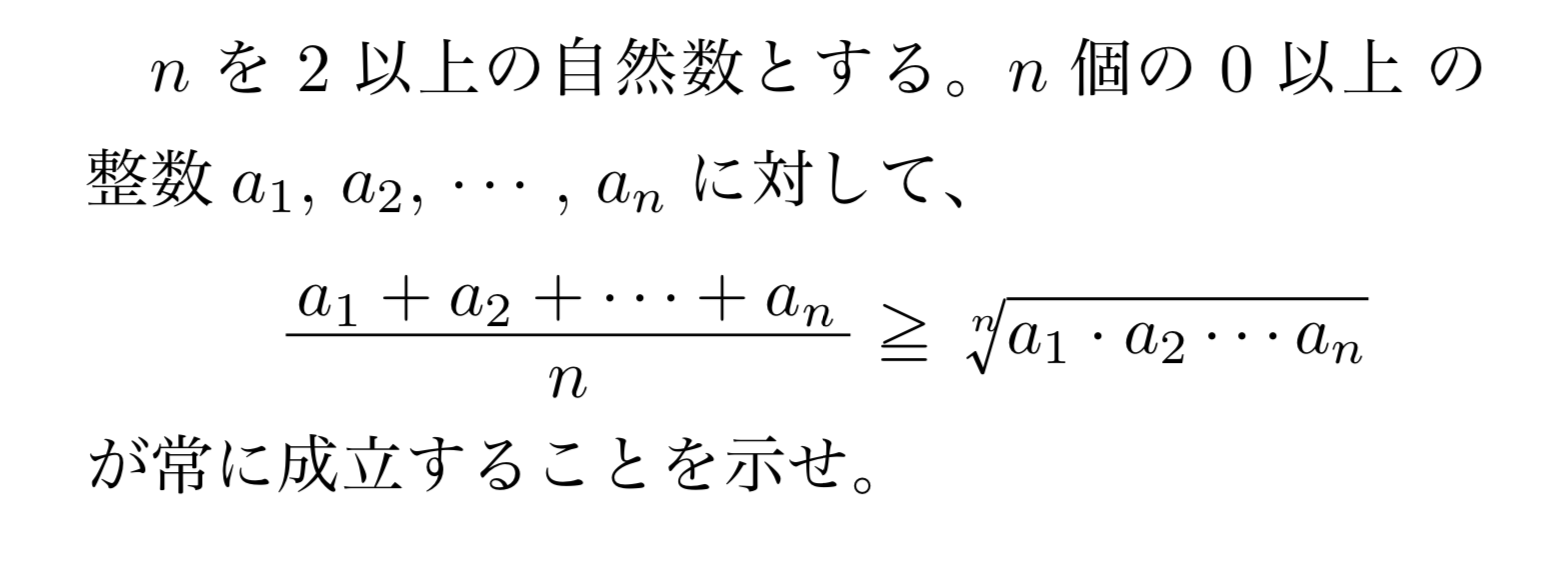
これはいわゆる相加相乗平均の大小関係の一般化された形ですね。これの非常に簡単な証明は以下の記事に書いてあります。

相加相乗平均の大小関係の証明や使い方、入試問題などを解説！

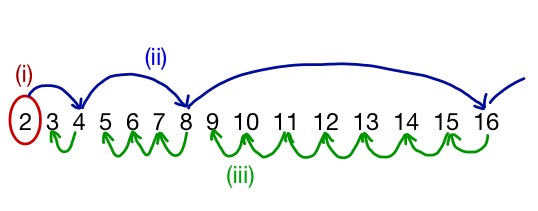
これを数学的帰納法によって示すときには、「$n=2$で成り立つこと」、「$n=2^m(mは自然数)$で成り立つならば$n=2^{m+1}$でも成り立つこと」、「$n=k(kは3以上の自然数)$で成り立つならば$n=k-1$でも成り立つこと」の3つを示すことによって証明ができます。

このように、指数関数的に大きくなるような$n$についてまず示して、そのあと小さくなる方向に1つずつ進む形で数学的帰納法の議論を構築するという方法もあるわけですね。

双方向帰納法の論理の流れは以下のような図で捉えておくとわかりやすいでしょう。

数学的帰納法はいつ使うか？

数学的帰納法がどんなものかは分かっていても、いつ使うべきかが分かっていないと大学入試に活かせないですよね。もちろん数学的帰納法を使うタイミングは以下の3つのときが多いことを知っておくとよいでしょう。

漸化式の問題

数学的帰納法は$n=k$のときの成立と$n=k+1$のときの成立を結びつける議論が最も重要な部分であることを考えると、その2つの状況の繋がりが明確であるほど数学的帰納法との相性が良いと言えます。

このような場合の代表例が漸化式が関わる問題のときです。漸化式によって定義された数列では$a_k$と$a_{k+1}$の関係が式で与えられているので、数学的帰納法を用いるときに漸化式に代入するだけで簡単に示せる場合が多いです。

整数問題

整数問題では、上で説明した無限降下法が登場することがしばしばあります。答えを求めるだけの整数問題の解き方は以下の記事にまとめられていますが、整数に関する証明問題については、無限降下法のような発展的手法を用いることがしばしばあるので注意したいところです。

整数問題の解き方は？大学入試の難問・良問を例に解説！

無限降下法は過去に東大でも出題されたことがあるのでマスターしておきたいですね。

不等式の証明問題

自然数$n$が含まれている不等式の証明問題も数学的帰納法を利用する可能性が高いです。これは、先ほどの漸化式が出てきたときに数学的帰納法が有効であるのと同様の理由によります。

不等式の各辺の形を$n$から$n+1$の形に変えるのを、あるものを足したりかけたりするだけで実現できる場合が多く、$n=k$のときと$n=k+1$のときの関係が簡単であることが多いので数学的帰納法との相性がよいです。

数学的帰納法の記述の書き方のコツ

数学的帰納法の記述の書き方についても学んでいきましょう！

記述の最初に数学的帰納法で示すことを明記する

数学的帰納法を用いて証明するときには、記述の一番最初に数学的帰納法を用いることを必ず書きましょう！

このように書けばよいでしょう。このときに、示すべき命題に番号を振っておくと、あとで参照するときに便利です。

また、試験によっては、「数学的帰納法によって示す」と書いているだけで部分点が入るケースがあるため、これは最後ではなく最初に書いておくのが望ましいです。

n=k+1のときの成立になにが必要か調べる

数学的帰納法の記述では$n=1$のときの成立を確認する部分を先に書いて、そのあとに$n=k$のときの成立を仮定して$n=k+1$のときの成立を示す部分がくることが多いですが、$n=k+1$のときの成立を示すためには何が必要かをチェックする作業をまず最初にするのがコツです。

なぜならば、$n=1$のとき〜と書き始めてしまったあとに、実は$n=k,\,k+1$のときを仮定して$n=k+2$のときの成立を示すパターンの数学的帰納法だった場合に、あとからすべて書き直すのは面倒になってしまうからです。

そこで、先に後半部分の議論がどのようになるかをチェックすることによって、2つ前までの情報が必要だとわかっていれば、$n=1,\,2$のときをチェックする記述から書き始めることができます。

新しい文字の定義を書き忘れない

数学的帰納法の記述の間違いでよくあるのが「$n=k$のときの成立を仮定する。」とだけ書いてしまって、$k$の定義がどこにも書かれていない場合です。

数学的帰納法の記述の書き方はテンプレのようなものがあることから$k$は自然数だということもわかりきっているわけですが、必ず「kは自然数」というのを書き忘れないように気をつけてくださいね。

最後に「数学的帰納法より」と書く必要はない

参考書によっては、記述のはじめにも最後にも「数学的帰納法より」という文言を書いているものがありますが、これは全くもって必要ないです。

一番最初に「数学的帰納法より」と書いておけば問題ないので、最後の記述は「以上より、題意成立。」くらいのことを書いておけば十分でしょう。

数学的帰納法が関わる入試問題5選

数学的帰納法について理解できたらあとは演習を積んでいきましょう！東大で出題されたものなど、難しい入試問題も混ざっていますが、頑張って解いてみてください。

問題1

解答・解説

1997年の東大文系数学第一問で出題された問題です。$n=k,\,k+1$のときの成立を仮定するパターンの説明に用いた例題の類題に当たります。

$a^{k+1}+b^{k+1}$を$a^k+b^k$で表そうと変形してみると、

$$a^{k+1}+b^{k+1}=(a+b)(a^k+b^k)-ab(a^{k-1}+b^{k-1})$$

となるので、$n=k-1$のときの成立も仮定しなければならないことに気づきます。そこで、$n=k,\,k+1$での成立を仮定して$n=k+2$のときの成立を示すパターンの帰納法を使おうとなるわけですね。

与えられた式は$a,\,b$の対称式になっているので、基本対称式である$a+b$と$ab$をひとかたまりと見て変形を進めていくとよいでしょう。

以下、解答例です。

問題2

解答・解説

これは、2017年の東大理系数学第四問で出題された問題です。整数問題を解く過程で数学的帰納法を用いるパターンですね。

(3)の証明で数学的帰納法を用います。また、(4)では最大公約数を求めるために$n$が小さい方向に降りていく議論をしていきます。背理法を使うわけではないので、無限降下法とは異なりますが、無限降下法の説明に用いた例題と状況が近いのが分かるかと思います。

解説は以下の記事を読んでください！

東大理系数学2017の入試問題・解答解説・難易度

問題3

解答・解説

2010年度の京大理系数学第四問の問題です。数列について漸化式ではなく、不等式のみが与えられています。例えば、$n=1$のときであれば、

$$0\leqq 3a_1\leqq a_1$$

となるので、$a_1=0$が分かるわけですね。一般の$a_n$に対しても同様の議論を適用したいところですが、$a_1$から$a_{n-1}$がどのようになっているかが分かっていないと与えられた不等式を上手く使えないことに気づきます。

そこで、$n\leqq k$のときの成立を仮定するパターンの帰納法を使うことになります。

問題4

解答・解説

まず、問題の状況がよく把握できない人が多いと思うので、具体的な時を考えることから始めてみましょう。例えば、$S_4$であれば、

$$1-\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{13}{12}$$

などになる可能性があり、それぞれの項の符号の選び方は2通りずつあるので、全部で$2^4$通りの可能性があることになります。

このときに、適切に符号を選んであげれば、必ず$S_n$の絶対値が$\frac{1}{n}$以下になることを示しにいきたいわけです。$S_4$の例で言えば、

$$1-\frac{1}{2}-\frac{1}{3}-\frac{1}{4}=-\frac{1}{12}$$

とすれば、絶対値は$\frac{1}{4}$以下になっているのでOKです。このような状況が必ず存在することを示すのにはどうすればよいでしょうか？

$S_n$の符号の選び方は$2^n$通りあって、それをすべて調べることはできないので、直接示すのは難しそうです。そこで、「すでに絶対値が小さいものを少し調整してさらに絶対値の小さいものを作る」ことなら簡単にできそうだと気づきます。

例えば、すでに$|S_k|\leqq \frac{1}{k}$を満たしているときに、$\frac{1}{k+1}$か$-\frac{1}{k+1}$を加えることによってさらに絶対値を小さくするのは簡単にできますよね。そこで数学的帰納法の利用を考えることになります。

以下、解答例です。

$a_{k+1}$の選び方が$S_k$が$0$以上なのか$0$以下なのかで変わることにも注意しましょう。

問題5

解答・解説

積分によって定められた関数の漸化式の問題です。「こんな漸化式の解き方習ったことないよ！」と思うものが出てきたら、とりあえず、小さな$n$についてどのようになっているか調べてみて、一般項を予想して帰納法に乗せるのが有効です。

実際、調べてみると、$f_1(x)=1+x$、$f_2(x)=1+x+\frac{x^2}{2}$、$f_3(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}$となるので、

$$f_n(x)=\sum_{k=0}^{n}\frac{x^k}{k!}$$

となるのではないかと予想がつきます。あとは数学的帰納法でこれを証明するだけです。

(2)はかなり難しい問題です。$n$が偶数のときと$n$が奇数のときで別の命題を示すことになるので、まずは偶数の方から示すことを考えます。

$f_n(x)>0$であることを示すには、$f_n(x)$の最小値が正であることを示せばOKですね。そこで、微分してみると、

$$f_n'(x)=\sum_{k=1}^{n}\frac{kx^k}{k!}=\sum_{k=0}^{n-1}\frac{x^k}{(k-1)!}=f_{n-1}(x)$$

となります。増減表を描くために$f_{n-1}(x)$の符号の変化を知りたいんですが、これはよく分かりませんね。

一旦これは置いておいて、$n$が奇数のときの証明を考えてみます。$f_n(x)=0$がただ1つの実数解を持つことを示すには、$f_n(x)$が単調増加するか単調減少するかを示すことが多いですよね。そこで、微分してみると、

$$f_n'(x)=f_{n-1}(x)$$

となるので、これが常に正か負かであることを示せばいいわけです。ここで問題文を見てみると、$n$が偶数のときは常に正であることが示せるようなので、それを仮定しておけば、

$$f_n^{\prime}(x)=f_{n-1}(x)>0$$

が言えることに気づきます。

さらに、先ほど考えた$n$が偶数の場合も、$n$が奇数のときにただ1つの実数解を持つことが成り立っていれば、そのときに最小値になるので、証明できそうです。

したがって、これらは片方が示されていればもう一方も示せるという関係になっていて、これらをまとめて数学的帰納法によって示すことができそうです！

よって、2つの命題をまとめて数学的帰納法に乗せることになります。

以下、解答例です。

2つの命題を一気に数学的帰納法で示すという今回の解き方は上で紹介したどのパターンにも属さないので、なかなか議論のしかたが思いつきづらかったかと思います。

まとめ